10.2.2: Desigualdades en varios pasos
- Page ID
- 111422
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Utilizar las propiedades de la desigualdad juntas para aislar variables y resolver desigualdades algebraicas, y expresar sus soluciones gráficamente.
- Simplifica y resuelve desigualdades algebraicas usando la propiedad distributiva para borrar paréntesis y fracciones.
Introducción
Resolver desigualdades de varios pasos es muy similar a resolver ecuaciones: lo que haces a un lado, necesitas hacer al otro lado para mantener el “equilibrio” de la desigualdad. Las propiedades de la desigualdad pueden ayudarte a entender cómo sumar, restar, multiplicar o dividir dentro de una desigualdad.
Usar propiedades juntas para resolver desigualdades
Una estrategia popular para resolver ecuaciones, aislando la variable, también se aplica a la resolución de desigualdades. Al sumar, restar, multiplicar y/o dividir, se puede reescribir la desigualdad para que la variable esté en un lado y todo lo demás esté del otro. Al igual que con las desigualdades de un solo paso, las soluciones a las desigualdades de varios pasos se pueden graficar en una recta numérica.
Resolver para p.
\(\ 4 p+5<29\).
Solución
|
\ (\\ begin {array} {r} |
Empezar a aislar la variable restando 5 de ambos lados de la desigualdad. |
| \(\ p<6\) | Dividir ambos lados de la desigualdad por 4 para expresar la variable con un coeficiente de 1. |
\(\ p<6\)
Para graficar esta desigualdad, dibujas un círculo abierto en el punto final, 6, en la recta numérica. El círculo está abierto porque la desigualdad es menor de 6 y no igual a 6. Los valores donde\(\ p\) es menor que 6 se encuentran a lo largo de la línea numérica a la izquierda de 6. Dibuja una línea azul con una flecha en la recta numérica apuntando en esa dirección.
Para verificar la solución, sustituya el punto final, 6, en la desigualdad original escrita como una ecuación, que se llama la ecuación relacionada, para ver si obtienes una declaración verdadera. Entonces revisa otra solución, como 0, para ver si la desigualdad es correcta.
Comprobar que\(\ p<6\) es la solución a la desigualdad\(\ 4 p+5<29\).
Solución
| \ (\\ begin {alineado} 4 p+5 &=29\\ \ text {Hace} 4 (6) +5 &=29? \\ 24+5 &=29\\ 29 &=29\ text {¡Sí! } \ end {alineado}\) |
Verifique el punto final, 6, en la ecuación relacionada. |
| \ (\\ begin {alineado} 4 p+5 &<29\\ \ text {Es} 4 (0) +5 &<29? \\ 0+5 &<29\\ 5 &<29\ text {¡Sí! } \ end {alineado}\) |
Prueba otro valor para comprobar la desigualdad. Vamos a usar\(\ p=0\). |
\(\ p<6\)es la solución a la desigualdad\(\ 4 p+5<29\).
Resolver para\(\ x\).
\(\ 3 x-7 \geq 41\)
Solución
|
\ (\\ begin {array} {r} |
Empezar a aislar la variable sumando 7 a ambos lados de la desigualdad. Dividir ambos lados de la desigualdad por 3 para expresar la variable con un coeficiente de 1. |
|
Cheque \ (\\ begin {aligned} \ (\\ begin {alineado} |
Primero, verifique el punto final, 16, en la ecuación relacionada. Entonces, intenta otro valor para comprobar la desigualdad. Vamos a usar\(\ x=20\). |
\(\ x \geq 16\)
Al resolver ecuaciones de varios pasos, preste atención a situaciones en las que multiplique o divida por un número negativo. En estos casos, se debe revertir el signo de desigualdad.
Resolver para\(\ p\).
\(\ -6 p+14<-58\)
Solución
| \ (\\ begin {array} {r} -6 p+14<&-58\\ \ -14\\\\\ &-14\ \\ hline\ frac {-6 p} {-6}\\\\\\\\\ >&\ frac {-72} {-6}\\ p>&12 \ end {array}\\) |
Empezar a aislar la variable restando 14 de ambos lados de la desigualdad. Dividir ambos lados de la desigualdad entre -6 para expresar la variable con un coeficiente de 1. Dividir por un número negativo da como resultado revertir el signo de desigualdad. |
|
Cheque \ (\\ text {Hace}\ comienza {alineado} |
Consulta la solución. Primero, verifique el punto final, 12, en la ecuación relacionada. |
| \ (\\ begin {alineado} -6 p+14 &<-58\\ \ text {Es} -6 (100) +14 &<-58? \\ -600+14 &<-58\\ -586 &<-58\ text {¡Sí! } \ end {alineado}\) |
Entonces, intenta otro valor para comprobar la desigualdad. Prueba 100. |
\(\ p>12\)
La gráfica de la desigualdad\(\ p>12\) tiene un círculo abierto a las 12 con una flecha que se extiende hacia la derecha.
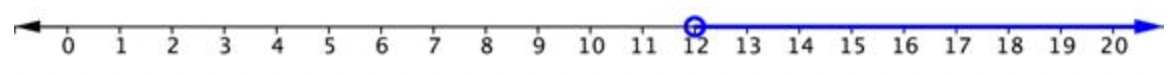
Resolver para\(\ x\).
\(\ \frac{1}{3}(x+3)+\frac{1}{2}>-\frac{9}{2}\).
Solución
| \ (\\ comenzar {alineado} \ frac {1} {3} (x+3) +\ frac {1} {2} -\ frac {1} {2} &>-\ frac {9} {2} -\ frac {1} {2}\ \ frac {1} {3} (x+3) &>-\ frac {10} {2}\ \ frac ac {1} {3} (x+3) &>-5\\ 3\ cdot\ frac {1} {3} (x+3) &>3\ cdot (-5) \\ x+3 &>-15\\ x+3-3 &>-15-3\\ x &>-18 \ fin {alineado}\) |
Para aislar la variable, restar\(\ \frac{1}{2}\) de ambos lados de la desigualdad. Después multiplica por 3 para que el coeficiente delante de los paréntesis sea 1. Después restar 3 de ambos lados. |
|
Cheque \ (\\ begin {alineado} |
Consulta la solución. Primero, verifique el punto final, -18, en la ecuación relacionada. |
| \ (\\ begin {array} {r} \ frac {1} {3} (0+3) +\ frac {1} {2} >-\ frac {9} {2}\ \ frac {1} {3} (3) +\ frac {1} {2} >-\ frac {9} {2} {2}\ 1+\ frac {1} {2} >\ frac {9} {2}\ \ frac {2} {2} +\ frac {1} {2} >-\ frac {9} {2}\\ \ frac {3} {2} >-\ frac {9} {2} \ end {array}\) |
Ahora comprueba cualquier valor para\(\ x\) eso que esté dentro de la región\(\ x>-18\). Vamos a utilizar\(\ x=0\). |
| El enunciado es cierto. |
\(\ x>-18\)
Un estudiante está resolviendo la desigualdad\(\ \frac{5}{2}+7 x \leq 4 x-\frac{7}{2}\). Si combina términos similares, ¿cuál de las siguientes desigualdades podría ver?
- \(\ -6 \leq 3 x\)
- \(\ 3 x \leq-6\)
- \(\ \frac{19 x}{2} \leq \frac{x}{2}\)
- \(\ x \leq \frac{-6 x}{7}\)
- Contestar
-
- Incorrecto. Parece que intentaste combinar términos similares pero cometiste errores de señal al sumar y restar. Para aislar el término variable a la derecha, es necesario restar\(\ 7 x\) de ambos lados;\(\ 4 x-7 x=-3 x\). La respuesta correcta es:\(\ 3 x \leq-6\).
- Correcto. Combinaste correctamente términos similares. \(\ \frac{5}{2}+7 x \leq 4 x-\frac{7}{2}\)se convierte\(\ 7 x-4 x \leq-\frac{7}{2}-\frac{5}{2}\). que es lo mismo que\(\ 3 x \leq-6\).
- Incorrecto. Recuerda que no puedes agregar términos variables y no variables como agregas enteros. La respuesta correcta es:\(\ 3 x \leq-6\).
- Incorrecto. Intenta restar\(\ \frac{5}{2}\) y\(\ 4x\) de cada lado antes de recolectar términos similares. La respuesta correcta es:\(\ 3 x \leq-6\).
Uso de la propiedad distributiva para borrar paréntesis y fracciones
Al igual que con las ecuaciones, la propiedad distributiva se puede aplicar para simplificar expresiones que forman parte de una desigualdad. Una vez que se hayan despejado los paréntesis, resolver la desigualdad será sencillo.
Resolver para\(\ x\).
\(\ 2(3 x-5) \leq 4 x+6\)
Solución
| \ (\\ begin {array} {rr} 2 (3 x-5) &\ leq & 4 x+6\\ 6 x-10 &\ leq &\ leq & 4 x+6\\ -4 x\\\\\\\\\ & -4 x\\\\\ \ hline 2 x-10 &\ leq & 6\\\ +10 && +10\\ \ hline\ frac {2 x} {2}\\\\\\\ &\ leq &\ frac {16} {2}\\ x\\\\\\\\\\ &\ leq & 8 \ end {array}\) |
Distribuir para borrar los paréntesis. Restar\(\ 4x\) de ambos lados para obtener el término variable en un solo lado. Agrega 10 a ambos lados para aislar la variable. Divide ambos lados por 2 para expresar la variable con un coeficiente de 1. |
|
Cheque \ (\\ begin {aligned} \ (\\ comenzar {alineado}\ texto {Es} |
Consulta la solución. Primero, verifique el punto final, 8, en la ecuación relacionada. Entonces, elija otra solución y evalúe la desigualdad para ese valor para asegurarse de que es una verdadera afirmación. Prueba 0. |
\(\ x \leq 8\)
Resolver para\(\ a\).
\(\ \frac{2 a-4}{6}<2\)
Solución
| \(\ 6 \cdot \frac{2 a-4}{6}<2 \cdot 6\) | Borrar la fracción multiplicando ambos lados de la ecuación por 6. |
| \ (\\ begin {array} {r} 2 a-4<&12\\ \ +4\\\\\ &+4\\\ hline \ frac {2 a} {2}\\\\\\\ <&\ frac {16} {2} \ end {array}\) |
Agrega 4 a ambos lados para aislar la variable. |
| \(\ a<8\) | Divide ambos lados por 2 para expresar la variable con un coeficiente de 1. |
|
Cheque \ (\\ begin {alineado} |
Consulta la solución. Primero, verifique el punto final, 8, en la ecuación relacionada. |
| \ (\\ begin {alineado}\ text {Is} \ frac {2 (5) -4} {6} &<2? \\ \ frac {10-4} {6} &<2\\ \ frac {6} {6} &<2\\ 1 &<2\ text {¡Sí! } \ end {alineado}\) |
Entonces, elija otra solución y evalúe la desigualdad para ese valor para asegurarse de que es una verdadera afirmación. Prueba 5. |
\(\ a<8\)
Resolver para\(\ d\).
\(\ \frac{3}{5}(2 d-5) \leq 4\left(7-\frac{1}{5} d\right)\)
Solución
| \ (\\ comenzar {alineado} \ frac {3} {5} (2 d-5) &\ leq 4\ izquierda (7-\ frac {1} {5} d\ derecha)\ \ frac {3} {5} (2 d) +\ frac {3} {5} (-5) &\ leq 4 (7) +4\ izquierda (-\ frac {1} {5} d\ derecha)\\ \ frac {6 d} {5} +\ izquierda (\ frac {-15} {5}\ derecha) &\ leq 28+\ izquierda (\ frac {-4 d} {5}\ derecha)\ \ frac {6 d} {5} -3 &\ leq 28-\ frac {4 d} {5} \ end {alineado}\) |
Esta desigualdad contiene dos paréntesis. Utilice la propiedad distributiva para expandir ambos lados de la desigualdad. |
| \ (\\ comenzar {alineado} \ frac {6 d} {5} -3+3 &\ leq 28-\ frac {4 d} {5} +3\ \\ frac {6 d} {5} &\ leq 31-\ frac {4 d} {5}\ \ frac {6 d} {5} +\ frac {4 d} {5} y\ leq 31-\ frac {4 d} {5} +\ frac {4 d} {5}\ \ frac {10 d} {5} & amp;\ leq 31\\ 2 d &\ leq 31\\ \ frac {2 d} {2} &\ leq\ frac {31} {2}\\ d &\ leq\ frac {31} {2} \ end {alineado}\) |
Ahora que ambos lados se han expandido, combina términos similares y encuentra el rango de valores para\(\ d\). |
| \ (\\ comenzar {alineado} \ frac {3} {5}\ izquierda (2\ cdot\ frac {31} {2} -5\ derecha) &=4\ izquierda (7-\ frac {1} {5}\ cdot\ frac {31} {2}\ derecha)\ \ frac {3} {5}\ izquierda (\ frac {62} {2} -5\ derecha) &=4\ izquierda (7-\ frac {31} {10}\ derecha)\\ \ frac {3} {5} (31-5) &=4\ izquierda (\ frac {70} {10} -\ frac {31} {10}\ derecha)\ \ frac {3} {5} (26) &=4\ izquierda (\ frac {39} {10}\ derecha)\ \ frac {78} {5} &=4\ izquierda (\ frac {39} {10}\ derecha)\ \ frac {78} {5} =\ frac {156} {10}\ \ frac {78} {5} &=\ frac {78} { 5}\ cdot\ frac {2} {2}\ \ frac {78} {5} &=\ frac {78} {5} \ end {alineado}\) |
Consulta la solución. Primero, verifique el punto final,\(\ \frac{31}{2}\), en la ecuación relacionada. |
| Se traduce en una verdadera afirmación. | |
| \ (\\ comenzar {alineado} \ frac {3} {5} (2\ cdot 0-5) &\ leq 4\ izquierda (7-\ frac {1} {5}\ cdot 0\ derecha)\ \ frac {3} {5} (0-5) &\ leq 4 (7-0)\ \ frac {3} {5} (-5) &\ leq 4 (7)\\ \ frac {-15} {5} &\ leq 28\\ -3 &\ leq 28 \ final {alineado}\) |
Ahora prueba cualquier valor para\(\ d\) que esté dentro de la región\(\ d \leq \frac{31}{2}\). Lo intentaremos\(\ d=0\). |
| Esta es también una verdadera afirmación. |
\(\ d \leq \frac{31}{2}\)
Cuál es el primer paso más lógico para resolver para la variable en la desigualdad:\(\ 8 x+7<3(2 x+1)\)
- Invierta el signo de desigualdad.
- Utilice la propiedad distributiva para borrar los paréntesis multiplicando cada uno de los términos entre paréntesis por 3.
- Restar\(\ 2x\) de ambos lados de la desigualdad.
- Dividir ambos lados de la desigualdad por 3.
- Contestar
-
- Incorrecto. El signo de desigualdad se invierte como resultado de dividir o multiplicar ambos lados de una desigualdad por un número negativo. Esto suele ocurrir como un paso posterior en una desigualdad de varios pasos y, en el caso de este ejemplo, no sucederá en absoluto. La respuesta correcta es usar la propiedad distributiva para borrar los paréntesis multiplicando cada uno de los términos entre paréntesis por 3.
- Correcto. La propiedad distributiva borra los paréntesis para que pueda aislar la variable.
- Incorrecto. Es necesario distribuir los 3 antes de restar cualquier término con\(\ x\) en él. La respuesta correcta es usar la propiedad distributiva para borrar los paréntesis multiplicando cada uno de los términos entre paréntesis por 3.
- Incorrecto. Dividir ambos lados por 3, aunque legal hacer, resultará en una fracción complicada en el lado izquierdo de la desigualdad y no es un primer paso lógico. La respuesta correcta es usar la propiedad distributiva para borrar los paréntesis multiplicando cada uno de los términos entre paréntesis por 3.
Resolver para\(\ x\):\(\ 5[2(3-x)-1] \leq 27\)
- \(\ x \leq-5\)
- \(\ x \leq 27\)
- \(\ x \geq \frac{1}{8}\)
- \(\ x \geq-\frac{1}{5}\)
- Contestar
-
- Incorrecto. Intenta sustituir en la desigualdad cualquier valor que sea menor o igual\(\ x\) a\(\ -5\) para. No obtendrá una declaración verdadera, por lo que no\(\ x\) es menor o igual a -5. La respuesta correcta es:\(\ x \geq-\frac{1}{5}\).
- Incorrecto. Es necesario evaluar el lado izquierdo de la desigualdad y luego resolver para\(\ x\). Recuerda eso\(\ 5[2(3-x)-1]=5[6-2 x-1]\). La respuesta correcta es:\(\ x \geq-\frac{1}{5}\).
- Incorrecto. Asegúrate de estar evaluando correctamente el lado izquierdo de la desigualdad:\(\ 5[2(3-x)-1]=5[6-2 x-1]\). La respuesta correcta es:\(\ x \geq-\frac{1}{5}\).
- Correcto. Evaluando primero los paréntesis interiores, lo encuentras\(\ 5[2(3-x)-1]=5[6-2 x-1]=5[5-2 x]=25-10 x\). Resolviendo para\(\ x\), restas 25 de ambos lados y luego divides por -10, lo que requiere voltear el signo de desigualdad de ≤ a ≥.
Resumen
Las desigualdades pueden tener una variedad de respuestas. Las soluciones a menudo se representan en una línea numérica para visualizar todas las soluciones. Las desigualdades de varios pasos se resuelven usando los mismos procesos que funcionan para resolver ecuaciones con una excepción. Cuando multiplicas o divides ambos lados de una desigualdad por un número negativo, debes invertir el símbolo de desigualdad. Los símbolos de desigualdad permanecen iguales cada vez que sumas o restas números positivos o negativos a ambos lados de la desigualdad.