11.1.1: Notación exponencial

Última actualización
Guardar como PDF

Page ID: 111464

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Evaluar expresiones que contengan exponentes.
Evaluar las notaciones exponenciales con exponentes 0 de 1 y.
Escribir una expresión exponencial que involucre exponentes negativos con exponentes positivos.

Introducción

Se necesita un lenguaje común para comunicar las ideas matemáticas de manera clara y eficiente. La notación exponencial es un ejemplo. Fue desarrollado para escribir multiplicaciones repetidas de manera más eficiente. Por ejemplo, el crecimiento ocurre en los organismos vivos por la división de las células. Un tipo de celda se divide 2 veces en una hora. Entonces en 12 horas, la celda dividirá los$\ 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2$ tiempos. Esto se puede escribir de manera más eficiente como$\ 2^{12}$.

Vocabulario exponencial

Utilizamos notación exponencial para escribir multiplicación repetida,$\ 10 \cdot 10 \cdot 10$ como por ejemplo$\ 10^{3}$. El 10 in$\ 10^{3}$ se llama la base. El 3 in$\ 10^{3}$ se llama el exponente. La expresión$\ 10^{3}$ se llama expresión exponencial.

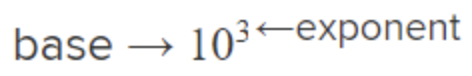
$Screen Shot 2021-06-06 at 2.31.40 PM.png$

$\ 10^{3}$se lee como “10 al tercer poder” o “10 elevado al poder de 3” o “10 cubos”. Significa$\ 10 \cdot 10 \cdot 10$, o mil.
$\ 8^{2}$se lee como “8 a la segunda potencia” o “8 elevado a la potencia de 2” o “8 al cuadrado”. Significa$\ 8 \cdot 8$, o 64.
$\ 5^{4}$se lee como “5 al cuarto poder” o “5 elevado al poder de 4”. Significa$\ 5 \cdot 5 \cdot 5 \cdot 5$, o 625.
$\ b^{5}$se lee como “$\ b$al quinto poder” o “$\ b$elevado al poder del 5”. Significa$\ b \cdot b \cdot b \cdot b \cdot b$. Su valor dependerá del valor de$\ b$.

El exponente aplica sólo al número al que está al lado. Entonces en la expresión$\ x y^{4}$, sólo el$\ y$ se ve afectado por el 4. $\ x y^{4}$significa$\ x \cdot y \cdot y \cdot y \cdot y$.

Si la expresión exponencial es negativa, tal como$\ -3^{4}$, significa$\ -(3 \cdot 3 \cdot 3 \cdot 3)$ o -81.

Si -3 va a ser la base de la expresión exponencial, debe escribirse como$\ (-3)^{4}$, lo que significa$\ -3 \cdot-3 \cdot-3 \cdot-3$, o 81.

De igual manera,$\ (-x)^{4}=(-x) \cdot(-x) \cdot(-x) \cdot(-x)=x^{4}$. mientras$\ -x^{4}=-(x \cdot x \cdot x \cdot x)$.

Se puede ver que hay una gran diferencia, ¡así que hay que tener mucho cuidado!

Evaluación de expresiones que contienen exponentes

Evaluar expresiones que contienen exponentes es lo mismo que evaluar cualquier expresión. Sustituye el valor de la variable en la expresión y simplifica.

Puedes usar PEMDAS para recordar el orden en el que debes evaluar la expresión. Primero, evaluar cualquier cosa en Paréntesis o símbolos de agrupación. A continuación, busque Exponentes, seguidos de Multiplicación y División (leyendo de izquierda a derecha), y por último, Suma y Resta (nuevamente, leyendo de izquierda a derecha).

Entonces, cuando evalúes la expresión$\ 5 x^{3}$ if$\ x=4$, primero sustituya el valor 4 por la variable$\ x$. Después evaluar, usando orden de operaciones.

Ejemplo

Evaluar. $\ 5 x^{3} \text { if } x=4$

Solución

$\ 5 \cdot 4^{3}$	Sustituye 4 por la variable$\ x$.
$\ 5(4 \cdot 4 \cdot 4)=5 \cdot 64$	Evaluar$\ 4^{3}$.
$\ 320$	Multiplicar.

$\ 5 x^{3}=320 \text { when } x=4$

Observe la diferencia entre el ejemplo anterior y el de abajo.

Ejemplo

Evaluar. $\ (5 x)^{3} \text { if } x=4$

Solución

$\ (5 \cdot 4)^{3}$	Sustituye 4 por la variable$\ x$.
$\ 20^{3}$	Multiplicar.
$\ 20 \cdot 20 \cdot 20=8,000$	Evaluar$\ 20^{3}$.

$\ (5 x)^{3}=8,000 \text { when } x=4$

¡La adición de paréntesis marcó una gran diferencia!

Ejemplo

Evaluar. $\ x^{3} \text { if } x=-4$

Solución

$\ (-4)^{3}$	Sustituye -4 por la variable$\ x$.
$\ -4 \cdot-4 \cdot-4$	Evaluar.
$\ -4 \cdot-4 \cdot-4=-64$	Multiplicar.

$\ x^{3}=-64, \text { when } x=-4$

Ejercicio

Evaluar la expresión$\ -(2 x)^{4}, \text { if } x=3$.

1,296
-1,296
162
-162

Contestar

Incorrecto. Sustituir el valor de 3 por la variable$\ x$ y evaluar$\ -(2 \cdot 3)^{4}$. No aplique el signo negativo hasta después de haber evaluado la expresión$\ (6)^{4}$. La respuesta correcta es -1,296.
Correcto. Sustituir el valor de 3 por la variable$\ x$ y evaluar$\ -(2 \cdot 3)^{4}=-6^{4}=-1,296$.
Incorrecto. Sustituir el valor de 3 por la variable$\ x$ y evaluar$\ -(2 \cdot 3)^{4}$. Aplicar el exponente 4 al producto$\ 2 \cdot 3$, o 6. Después aplique el signo negativo. La respuesta correcta es -1,296.
Incorrecto. Sustituir el valor de 3 por la variable$\ x$ y evaluar$\ -(2 \cdot 3)^{4}$. Aplicar el exponente 4 al producto$\ 2 \cdot 3$, o 6. Después aplique el signo negativo. La respuesta correcta es -1,296.

Exponentes de Cero y Uno

¿Qué significa cuando un exponente es 0 o 1? Consideremos$\ 25^{1}$. Cualquier valor elevado a la potencia de 1 es solo el valor en sí. Esto tiene sentido, porque el exponente de 1 significa que la base se usa como factor sólo una vez. Entonces la base está sola, y$\ 25^{1}$ es simplemente 25.

Pero ¿qué pasa con un valor elevado al poder del 0? Usa lo que sabes sobre potencias de 10 para averiguar qué significa el poder de 0. A continuación se muestra una lista de potencias de 10 y sus valores equivalentes. Mira cómo cambian los números bajando por las columnas izquierda y derecha. ¿Puedes notar algún patrón ahí?

\ (\\ begin {array} {ccr}
\ bf\ text {Forma exponencial} &\ bf\ text {Forma expandida} &\ bf\ text {Valor}\\
10^ {5} & 10\ cdot 10\ cdot 10\ cdot 10\ cdot 10\
cdot 10\ cdot 10\ cdot 10\ cdot 10\ cdot 10 & 10,000\
10^ {3}} & 10\ cdot 10\ cdot 10 & 1,000\\
10^ {2} & 10\ cdot 10 & 100\\
10^ {1} & 10 & 10
\ end {array}\)

Al bajar la mesa, cada fila deja caer un factor de 10 del que está arriba. De la fila 1 a la fila 2, la forma exponencial va de$\ 10^{5}$ a$\ 10^{4}$. El valor cae de 100 mil a 10 mil. Otra forma de poner esto es que cada valor se divide por 10 para producir el siguiente valor abajo de la columna.

Usemos este patrón de división por 10 para predecir el valor de$\ 10^{0}$.

Siguiendo el patrón, se ve que$\ 10^{0}$ es igual a 1. ¿El patrón aguantaría para una base diferente? ¿Decir una base de 3?

\ (\\ begin {array} {ccr}
\ bf\ text {Forma exponencial} &\ bf\ text {Forma expandida} &\ bf\ text {Valor}\\
3^ {5} & 3\ cdot 3\ cdot 3\ cdot 3\ cdot 3\ cdot 3\ cdot 3 & 243\
3^ {4} & 3\ cdot 3\ cdot 3\ cdot 3 & 81\
3^ {3} & 3\ cdot 3\ cdot 3 & amp; 27\\
3^ {2} & 3\ cdot 3 & 9\\
3^ {1} & 3 & 3\
\ hline
3^ {0} & 1 & 1\\
\ hline
\ end {array}\)

¡Sí! Y el mismo patrón se mantendría cierto para cualquier número o variable distinta de cero elevada a una potencia de 0,$\ n^{0}=1$.

Hay un conflicto cuando la base es 0. Ya sabes eso$\ 0^{3}=0$$\ 0^{2}=0$,, y$\ 0^{1}=0$, así$\ 0^{0}$ esperarías ser también igual a 0. No obstante, el patrón anterior dice que cualquier base levantada a la potencia de 0 es 1, así que esto te lleva a creer eso$\ 0^{0}=1$. Observe los patrones competidores: ¡$\ 0^{0}$no puede ser tanto 0 como 1! En este caso, los matemáticos dicen que el valor de$\ 0^{0}$ es indefinido. (¡Y recuerda que undefined no es lo mismo que 0!)

Exponentes de 0 o 1

Cualquier número o variable elevada a una potencia de 1 es el número en sí. $\ n^{1}=n$

Cualquier número distinto de cero o variable elevada a una potencia de 0 es igual a 1. $\ n^{0}=1$

La cantidad$\ 0^{0}$ es indefinida.

Ejemplo

Evaluar. $\ 2 x^{0} \text { if } x=9$

Solución

$\ 2 \cdot 9^{0}$	Sustituye 9 por la variable$\ x$.
$\ 2 \cdot 1$	Evaluar$\ 9^{0}$.
$\ 2$	Multiplicar.

$\ 2 x^{0}=2, \text { if } x=9$

Como se hizo anteriormente, para evaluar expresiones que contengan exponentes de 0 o 1, sustituya el valor de la variable en la expresión y simplifique.

Ejercicio

Evaluar la expresión$\ 3 x^{0}-y^{1}, \text { if } x=12 \text { and } y=-6$.

42
-3
9
2

Contestar

Incorrecto. Sustituir el valor de 12 para la variable$\ x$ y -6 para la variable$\ y$:$\ 3 \cdot 12^{0}-(-6)^{1}$. Recuerda eso$\ 12^{0}=1$. La respuesta correcta es 9.
Incorrecto. Sustituir el valor de 12 para la variable$\ x$ y -6 para la variable$\ y$:$\ 3 \cdot 12^{0}-(-6)^{1}$. Recuerda eso$\ (-6)^{1}=-6$ y$\ -(-6)=6$. La respuesta correcta es 9.
Correcto. $\ 3 \cdot 12^{0}-(-6)^{1}=3 \cdot 1-(-6)^{1}=3 \cdot 1+6=9$
Incorrecto. Sustituir el valor de 12 para la variable$\ x$ y -6 para la variable$\ y$:$\ 3 \cdot 12^{0}-(-6)^{1}$. Recuerda que una base elevada a la potencia de 1 es la base. La respuesta correcta es 9.

Exponentes negativos

¿Qué significa cuando un exponente es un entero negativo? Usemos los poderes del patrón 10 de antes para averiguarlo. Si continúas con este patrón para agregar algunas filas más, más allá$\ 10^{0}$, encontrarás lo siguiente:

\ (\\ begin {array} {ccr}
\ bf\ text {Forma exponencial} &\ bf\ text {Forma expandida} &\ bf\ text {Valor}\\
10^ {5} & 10\ cdot 10\ cdot 10\ cdot 10\ cdot 10\
cdot 10\ cdot 10\ cdot 10\ cdot 10\ cdot 10 & 10,000\
10^ {3}} y 10\ cdot 10\ cdot 10 & 1,000\\
10^ {2} & 10\ cdot 10 & 100\\
10^ {1} & 10 & 10\\
10^ {0} & 1 & 1\
10^ {-1} &\ frac {1} {10^ {1}} &\ frac {1} {10}\
10^ {-2} &\ frac {1} {10^ {2} &\ frac {1} {100}
\ fin {matriz}\)

Siguiendo el patrón, se ve que$\ 10^{0}$ es igual a 1. Entonces te metes en exponentes negativos:$\ 10^{-1}$ es igual a$\ \frac{1}{10^{1}}$, y$\ 10^{-2}$ es lo mismo que (\\ frac {1} {10^ {2}}\).

Siguiendo este patrón, un número con un exponente negativo puede ser reescrito como el recíproco del número original, con un exponente positivo.

Por ejemplo,$\ 10^{-3}=\frac{1}{10^{3}}$ y$\ 10^{-7}=\frac{1}{10^{7}}$.

Para ver si estos patrones se mantienen verdaderos para números distintos al 10, consulta esta tabla con potencias de 3.

Los números son diferentes pero los patrones son los mismos. Ahora estamos listos para exponer la definición de un exponente negativo.

Exponente Negativo

Para cualquier número distinto de cero$\ n$ y cualquier entero$\ x$,$\ n^{-x}=\frac{1}{n^{x}}$. Por ejemplo,$\ 5^{-2}=\frac{1}{5^{2}}$.

Obsérvese que la definición anterior establece que la base,$\ n$ debe ser un “número distinto de cero”.

Ejercicio

Evaluar la expresión$\ \left(x^{-2}\right) \cdot\left(x^{0}\right)$ cuando$\ x=6$.

$\ \frac{1}{36}$
$\ \frac{1}{6}$
$\ 0$
$\ 36$

Contestar

Correcto. Sustituir el valor de 6 por la variable$\ x$ y evaluar. $\ 6^{-2} \cdot 6^{0}=\frac{1}{6^{2}} \cdot 6^{0}=\frac{1}{36} \cdot 1=\frac{1}{36}$.
Incorrecto. Sustituir el valor de 6 por la variable$\ x$ y evaluar:$\ 6^{-2} \cdot 6^{0}$. Recuerda eso$\ (6)^{0}=1$. La respuesta correcta es$\ \frac{1}{36}$.
Incorrecto. Sustituir el valor de 6 por la variable$\ x$ y evaluar:$\ 6^{-2} \cdot 6^{0}$. Recuerda eso$\ (6)^{0}=1$. La respuesta correcta es$\ \frac{1}{36}$.
Incorrecto. Sustituir el valor de 6 por la variable$\ x$ y luego evaluar:$\ 6^{-2} \cdot 6^{0}$ Recuerda eso$\ (6)^{-2}=\frac{1}{6^{2}}=\frac{1}{36}$. La respuesta correcta es$\ \frac{1}{36}$.

Resumen

La notación exponencial está compuesta por una base y un exponente. Es una forma “taquigráfica” de escribir multiplicación repetida, e indica que la base es un factor y el exponente es el número de veces que se utiliza el factor en la multiplicación. Las reglas básicas de los exponentes son las siguientes:

Un exponente aplica sólo al valor a su izquierda inmediata.
Cuando una cantidad entre paréntesis se eleva a una potencia, el exponente aplica a todo lo que esté dentro de los paréntesis.
Para cualquier número distinto de cero$\ n$,$\ n^{0}=1$.
Para cualquier número distinto de cero$\ n$ y cualquier entero$\ x$,$\ n^{-x}=\frac{1}{n^{x}}$.

\(\ 5 \cdot 4^{3}\)	Sustituye 4 por la variable\(\ x\).
\(\ 5(4 \cdot 4 \cdot 4)=5 \cdot 64\)	Evaluar\(\ 4^{3}\).
\(\ 320\)	Multiplicar.

\(\ (5 \cdot 4)^{3}\)	Sustituye 4 por la variable\(\ x\).
\(\ 20^{3}\)	Multiplicar.
\(\ 20 \cdot 20 \cdot 20=8,000\)	Evaluar\(\ 20^{3}\).

\(\ (-4)^{3}\)	Sustituye -4 por la variable\(\ x\).
\(\ -4 \cdot-4 \cdot-4\)	Evaluar.
\(\ -4 \cdot-4 \cdot-4=-64\)	Multiplicar.

\(\ 2 \cdot 9^{0}\)	Sustituye 9 por la variable\(\ x\).
\(\ 2 \cdot 1\)	Evaluar\(\ 9^{0}\).
\(\ 2\)	Multiplicar.