11.1.4: Notación científica

Última actualización
Guardar como PDF

Page ID: 111459

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Convertir entre notación científica y decimal.
Multiplicar y dividir usando notación científica.
Resolver problemas de aplicación.

Introducción

Cuando se trabaja con números muy grandes o muy pequeños, los científicos, matemáticos e ingenieros suelen utilizar la notación científica para expresar esas cantidades. La notación científica utiliza notación exponencial. Los siguientes son ejemplos de notación científica.

Año luz: número de millas que recorre la luz en un año, alrededor de 5,880,000,000,000

La notación científica es$\ 5.88 \times 10^{12}$ millas.

átomo de hidrógeno: tiene un diámetro de aproximadamente 0.00000005 milímetros

La notación científica es$\ 5 \times 10^{-8}$ milímetros

La computación con números muy grandes se hace más fácil con notación científica.

Aprendiendo a usar la notación científica

Cuando se escribe un número en notación científica, el exponente te indica si el término es un número grande o pequeño. Un exponente positivo indica un número grande y un exponente negativo indica un número pequeño que está entre 0 y 1.

Ya que es tan útil, veamos más de cerca los detalles del formato de notación científica.

Notación Científica

Un número positivo se escribe en notación científica si se escribe como$\ a \times 10^{n}$ donde el coeficiente$\ a$ tiene un valor tal que$\ 1 \leq a<10$ y$\ n$ es un entero.

Mira los números a continuación. ¿Cuál de los números está escrito en notación científica?

Número	¿Notación científica?	Explicación
$\ 1.85 \times 10^{-2}$	si	$\ 1 \leq 1.85<10$ -2 es un número entero
$\ 1.083 \times 10^{\frac{1}{2}}$	no	$\ \frac{1}{2}$no es un número entero
$\ 0.82 \times 10^{14}$	no	$\ 0.82$no es$\ \geq 1$
$\ 10 \times 10^{3}$	no	$\ 10$no es$\ <10$

Ejercicio

¿Qué número a continuación está escrito en notación científica?

$\ 4.25 \times 10^{0.08}$
$\ 0.425 \times 10^{7}$
$\ 42.5 \times 10^{5}$
$\ 4.25 \times 10^{6}$

Contestar

Incorrecto. El exponente debe ser un entero y 0.08 no es un entero. La respuesta correcta es$\ 4.25 \times 10^{6}$.
Incorrecto. Esto no está en notación científica porque 0.425 es menor que 1. La respuesta correcta es$\ 4.25 \times 10^{6}$.
Incorrecto. Esto no está en notación científica porque 42.5 es mayor que 10. La respuesta correcta es$\ 4.25 \times 10^{6}$.
Correcto. Esta es notación científica. 4.25 es mayor que 1 y menor que 10, y 6 es un número entero.

Escribir notación decimal en notación científica

Ahora comparemos algunos números expresados tanto en notación científica como en notación decimal estándar para entender cómo convertir de una forma a otra. Echa un vistazo a las tablas a continuación. Preste mucha atención al exponente en la notación científica y la posición del punto decimal en la notación decimal.

Números grandes
Notación decimal	Notación Científica
500.0	$\ 5 \times 10^{2}$
80,000.0	$\ 8 \times 10^{4}$
$\ 43,000,000.0$	$\ 4.3 \times 10^{7}$
$\ 62,500,000,000.0$	$\ 6.25 \times 10^{10}$

Números pequeños
Notación decimal	Notación Científica
$\ 0.05$	$\ 5 \times 10^{-2}$
$\ 0.0008$	$\ 8 \times 10^{-4}$
$\ 0.00000043$	$\ 4.3 \times 10^{-7}$
$\ 0.000000000625$	$\ 6.25 \times 10^{-10}$

Para escribir un número grande en notación científica, mueva el punto decimal hacia la izquierda para obtener un número entre 1 y 10. Ya que mover el punto decimal cambia el valor, hay que multiplicar el decimal por una potencia de 10 para que la expresión tenga el mismo valor.

Veamos un ejemplo.

\ (\\ begin {array} {r}
180,000 {\ color {rojo}.} =18,000 {\ color {rojo}.} 0\ veces 10^ {1}\\\\\\\\\\\\
1.800 {\ color {rojo}.} 00\ veces 10^ {2}\\\\\\\\
180 {\ color {rojo}.} 000\ veces 10^ {3}\\\\\
18 {\ color {rojo}.} 0000\ veces 10^ {4}\\\\\
1 { \ color {rojo}.} 80000\ times 10^ {5}
\ end {array}\)

Observe que el punto decimal se movió 5 lugares a la izquierda, y el exponente es 5.

Ejercicio

Se estima que la población mundial es de alrededor de 6,800,000,000 de personas. ¿Cuál respuesta expresa este número en notación científica?

$\ 7 \times 10^{9}$
$\ 0.68 \times 10^{10}$
$\ 6.8 \times 10^{9}$
$\ 68 \times 10^{8}$

Contestar

Incorrecto. La notación científica reescribe los números, no los redondea. La respuesta correcta es$\ 6.8 \times 10^{9}$.
Incorrecto. Si bien$\ 0.68 \times 10^{10}$ equivale a 6,800,000,000, 0.68 no es la forma para la notación científica ya que 0.68 no es un número entre 1 y 10. La respuesta correcta es$\ 6.8 \times 10^{9}$.
Correcto. El número$\ 6.8 \times 10^{9}$ equivale a 6,800,000,000 y utiliza el formato adecuado para cada factor.
Incorrecto. Si bien$\ 68 \times 10^{8}$ equivale a 6,800,000,000, no está escrito en notación científica ya que 68 no está entre 1 y 10. La respuesta correcta es$\ 6.8 \times 10^{9}$.

Pregunta Avanzada

Representar$\ 1.00357 \times 10^{-6}$ en forma decimal.

1.00357000000
0.000100357
0.000001357
0.00000100357

Contestar

Incorrecto. Añadió seis 0s al final del decimal. Esto no cambia en absoluto su valor; 1.00357000000=1.00357, que no es igual a$\ 1.00357 \times 10^{-6}$. La respuesta correcta es 0.00000100357.
Incorrecto. Moviste el punto decimal en la dirección correcta, pero no lo moviste suficientes lugares. La respuesta correcta es 0.00000100357.
Incorrecto. Moviste el punto decimal el número correcto de espacios, pero el número que creaste es diferente al número con el que empezaste:$\ 1.00357 \times 10^{-6} \neq 0.000001357$. Recuerda que los ceros entre 1 y 3 también deben incluirse en el número final. La respuesta correcta es 0.00000100357.
Correcto. El exponente es -6. Se movió el punto decimal 6 puntos hacia la izquierda, creando el decimal 0.00000100357.

Para escribir un número pequeño (entre 0 y 1) en notación científica, se mueve el decimal a la derecha y el exponente tendrá que ser negativo.

\ (\\ comenzar {array} {r}
0 {\ color {rojo}.} 00004=00 {\ color {rojo}.} 0004\ veces 10^ {-1}\\
000 {\ color {rojo}.} 004\ veces 10^ {-2}\\\
0000 {\ color {rojo}.} 04\ veces 10^ {-3}\\\\\ 00000 {\ color {rojo}.} 04\ veces 10^ {-3}\\\\\
00000 {\ color {rojo}.}.} 4\ veces 10^ {-4}\\\\\\\
000004 {\ color {rojo }.} \ times 10^ {-5}\\\\\\\\\
\ end {array}\)

$\ 0.00004=4 \times 10^{-5}$

Podrán notar que el punto decimal se movió cinco lugares a la derecha hasta que obtuvo el número 4, que está entre 1 y 10. El exponente es -5.

Escribir Notación Científica en Notación Decimal

También se puede escribir notación científica como notación decimal. Por ejemplo, el número de millas que recorre la luz en un año es$\ 5.88 \times 10^{12}$. $\ 5.88 \times 10^{12}$, y un átomo de hidrógeno tiene un diámetro de$\ 5 \times 10^{-8}$ mm. Para escribir cada uno de estos números en notación decimal, mueve el punto decimal el mismo número de lugares que el exponente. Si el exponente es positivo, mueva el punto decimal hacia la derecha. Si el exponente es negativo, mueva el punto decimal hacia la izquierda.

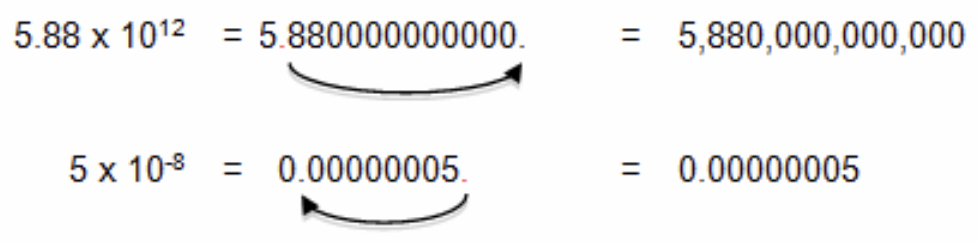
$Screen Shot 2021-06-08 a las 11.33.00 PM.png$

Por cada potencia de 10, se mueve el punto decimal un lugar. Ten cuidado aquí y no te dejes llevar por los ceros; el número de ceros después del punto decimal siempre será 1 menos que el exponente porque se necesita una potencia de 10 para desplazar ese primer número a la izquierda del decimal.

Ejercicio

Reescribir$\ 1.57 \times 10^{-10}$ en notación decimal.

15,700,000,000
0.000000000157
0.0000000000157
$\ 157 \times 10^{-12}$

Contestar

Incorrecto. Moviste el punto decimal en la dirección equivocada. El exponente es negativo, así que para convertir al formato decimal, mueva el punto decimal hacia la izquierda, no hacia la derecha. La respuesta correcta es 0.000000000157.
Correcto. La expresión tiene un exponente negativo, por lo que mueve el punto decimal 10 lugares a la izquierda para convertirlo a notación decimal, 0.000000000157.
Incorrecto. Insertó 10 ceros entre el número y el punto decimal. Mueva el punto decimal 10 lugares a la izquierda en su lugar. La respuesta correcta es 0.000000000157.
Incorrecto. Este número es equivalente al número original, pero no está en notación decimal. La respuesta correcta es 0.000000000157.

Multiplicar y dividir números expresados en notación científica

Los números que están escritos en notación científica se pueden multiplicar y dividir más bien simplemente aprovechando las propiedades de los números y las reglas de los exponentes que quizás recuerdes. Para multiplicar números en notación científica, primero multiplique los números que no sean potencias de 10 (la$\ a$ in$\ a \times 10^{n}$). Después multiplica las potencias de diez sumando los exponentes.

Esto producirá un nuevo número de veces una potencia diferente de 10. Todo lo que tienes que hacer es verificar para asegurarte de que este nuevo valor está en notación científica. Si no lo es, lo conviertes.

Veamos algunos ejemplos.

Ejemplo

$\ \left(3 \times 10^{8}\right)\left(6.8 \times 10^{-13}\right)$.

Solución

$\ (3 \times 6.8)\left(10^{8} \times 10^{-13}\right)$	Reagruparse, utilizando las propiedades conmutativas y asociativas.
$\ (20.4)\left(10^{8} \times 10^{-13}\right)$	Multiplicar los coeficientes.
$\ 20.4 \times 10^{-5}$	Multiplica las potencias de 10 usando la Regla del Producto: sumar los exponentes.
$\ \left(2.04 \times 10^{1}\right) \times 10^{-5}$	Convierte 20.4 en notación científica moviendo el punto decimal un lugar hacia la izquierda y multiplicando por 10 ¹.
$\ 2.04 \times\left(10^{1} \times 10^{-5}\right)$	Agrupar las potencias de 10 utilizando la propiedad asociativa de la multiplicación.
$\ 2.04 \times 10^{1+(-5)}$	Multiplicar usando la Regla del Producto: sumar los exponentes.

$\ \left(3 \times 10^{8}\right)\left(6.8 \times 10^{-13}\right)=2.04 \times 10^{-4}$

Ejemplo Avanzado

$\ \left(8.2 \times 10^{6}\right)\left(1.5 \times 10^{-3}\right)\left(1.9 \times 10^{-7}\right)$

Solución

$\ (8.2 \times1.5\times1.9)(10^6\times10^{-3}\times10^{-7})$	Reagruparse, utilizando las propiedades conmutativas y asociativas.
$\ (23.37)\left(10^{6} \times 10^{-3} \times 10^{-7}\right)$	Multiplique los números.
$\ 23.37 \times 10^{-4}$	Multiplica las potencias de 10 usando la Regla del Producto: sumar los exponentes.
$\ \left(2.337 \times 10^{1}\right) \times 10^{-4}$	Convierte 23.37 en notación científica moviendo el punto decimal un lugar hacia la izquierda y multiplicando por 10 ¹.
$\ 2.337 \times\left(10^{1} \times 10^{-4}\right)$	Agrupar las potencias de 10 utilizando la propiedad asociativa de la multiplicación.
$\ 2.337 \times 10^{1+(-4)}$	Multiplica usando la Regla del Producto y agrega los exponentes.

$\ \left(8.2 \times 10^{6}\right)\left(1.5 \times 10^{-3}\right)\left(1.9 \times 10^{-7}\right)=2.337 \times 10^{-3}$

Para dividir los números en notación científica, una vez más se aplican las propiedades de los números y las reglas de los exponentes. Empiezas dividiendo los números que no son potencias de 10 (el$\ a$ in$\ a \times 10^{n}$). Entonces divides los poderes de 10 restando los exponentes.

Esto producirá un nuevo número de veces una potencia diferente de 10. Si no está ya en notación científica, lo conviertes, y luego ya está.

Veamos algunos ejemplos.

Ejemplo

$\ \frac{2.829 \times 10^{-9}}{3.45 \times 10^{-3}}$

Solución

$\ \left(\frac{2.829}{3.45}\right)\left(\frac{10^{-9}}{10^{-3}}\right)$	Reagruparse, utilizando la propiedad asociativa.
$\ (0.82)\left(\frac{10^{-9}}{10^{-3}}\right)$	Dividir los coeficientes.
\ (\\ begin {array} {c} 0.82\ times 10^ {-9- (-3)}\\ 0.82\ times 10^ {-6} \ end {array}\)	Dividir los poderes de 10 usando la Regla del Cociente: restar los exponentes.
$\ \left(8.2 \times 10^{-1}\right) \times 10^{-6}$	Convierte 0.82 en notación científica moviendo el punto decimal un lugar a la derecha y multiplicando por 10 ^-1.
$\ 8.2 \times\left(10^{-1} \times 10^{-6}\right)$	Agrupar los poderes de 10 juntos usando la propiedad asociativa.
$\ 8.2 \times 10^{-1+(-6)}$	Multiplica las potencias de 10 usando la Regla del Producto: sumar los exponentes.

$\ \frac{2.829 \times 10^{-9}}{3.45 \times 10^{-3}}=8.2 \times 10^{-7}$

Ejemplo Avanzado

$\ \frac{\left(1.37 \times 10^{4}\right)\left(9.85 \times 10^{6}\right)}{5.0 \times 10^{12}}$

Solución

$\ \frac{(1.37 \times 9.85)\left(10^{6} \times 10^{4}\right)}{5.0 \times 10^{12}}$	Reagrupar los términos en el numerador según las propiedades asociativas y conmutativas.
$\ \frac{13.4945 \times 10^{10}}{5.0 \times 10^{12}}$	Multiplicar.
$\ \left(\frac{13.4945}{5.0}\right)\left(\frac{10^{10}}{10^{12}}\right)$	Reagruparse, utilizando la propiedad asociativa.
$\ (2.6989)\left(\frac{10^{10}}{10^{12}}\right)$	Dividir los números.
\ (\\ begin {array} {r} (2.6989)\ left (10^ {10-12}\ derecha)\\ 2.6989\ times 10^ {-2} \ end {array}\)	Dividir los poderes de 10 usando la Regla del Cociente: restar los exponentes.

$\ \frac{\left(1.37 \times 10^{4}\right)\left(9.85 \times 10^{6}\right)}{5.0 \times 10^{12}}=2.6989 \times 10^{-2}$

Observe que cuando divide términos exponenciales, resta el exponente en el denominador del exponente en el numerador.

Ejercicio

Evaluar$\ \left(4 \times 10^{-10}\right)\left(3 \times 10^{5}\right)$ y expresar el resultado en notación científica.

$\ 1.2 \times 10^{-4}$
$\ 12 \times 10^{-5}$
$\ 7 \times 10^{-5}$
$\ 1.2 \times 10^{-50}$

Contestar

Correcto. $\ 1.2 \times 10^{-4}$es un cálculo preciso y una notación científica correcta.
Incorrecto. Casi correcto, pero ahora hay que convertir el coeficiente 12 en notación científica. 12 es mayor que 10 y la notación científica requiere que este número sea mayor o igual a 1 e inferior a 10. La respuesta correcta es$\ 1.2 \times 10^{-4}$.
Incorrecto. Multiplicar, no sumar, los números 4 y 3. La respuesta correcta es$\ 1.2 \times 10^{-4}$.
Incorrecto. Sumar, no multiplicar, exponentes. La respuesta correcta es$\ 1.2 \times 10^{-4}$.

Pregunta Avanzada

Evaluar$\ \left(3.15 \times 10^{4}\right)\left(5.15 \times 10^{-7}\right)$ y expresar el resultado como decimal.

0.0162225
162225
0.000162225
16.2225

Contestar

Correcto. $\ 3.15 \times 5.15=16.2225$, y$\ 10^{4} \times 10^{-7}=10^{-3}$. El exponente es negativo, por lo que para convertir a formato decimal, mueva el punto decimal tres espacios hacia la izquierda para un valor de 0.0162225.
Incorrecto. La expresión tiene un exponente negativo, por lo que mueve el punto decimal 3 lugares a la izquierda, no a la derecha, para convertirlo a notación decimal. La respuesta correcta es 0.0162225.
Incorrecto. Se movió el punto decimal en la dirección correcta, pero no el número correcto de lugares. Recuerda eso$\ 10^{4} \times 10^{-7}=10^{-3}$, así que tienes que mover el punto decimal tres lugares a la izquierda. La respuesta correcta es 0.0162225.
Incorrecto. $\ 3.15 \times 5.15=16.2225$, pero parece que te olvidaste de multiplicar$\ 10^{4} \times 10^{-7}$. La respuesta correcta es 0.0162225.

Resumen

La notación científica se desarrolló para ayudar a matemáticos, científicos y otros a la hora de expresar y trabajar con números muy grandes y muy pequeños. La notación científica sigue un formato muy específico en el que un número se expresa como el producto de un número mayor o igual a 1 y menor de 10, y una potencia de 10. El formato se escribe$\ a \times 10^{n}$, donde$\ 1 \leq a<10$ y$\ n$ es un entero.

Para multiplicar o dividir números en notación científica, se pueden utilizar las propiedades conmutativas y asociativas para agrupar los términos exponenciales y aplicar las reglas de exponentes.

Número	¿Notación científica?	Explicación
\(\ 1.85 \times 10^{-2}\)	si	\(\ 1 \leq 1.85<10\) -2 es un número entero
\(\ 1.083 \times 10^{\frac{1}{2}}\)	no	\(\ \frac{1}{2}\)no es un número entero
\(\ 0.82 \times 10^{14}\)	no	\(\ 0.82\)no es\(\ \geq 1\)
\(\ 10 \times 10^{3}\)	no	\(\ 10\)no es\(\ <10\)

Notación decimal	Notación Científica
500.0	\(\ 5 \times 10^{2}\)
80,000.0	\(\ 8 \times 10^{4}\)
\(\ 43,000,000.0\)	\(\ 4.3 \times 10^{7}\)
\(\ 62,500,000,000.0\)	\(\ 6.25 \times 10^{10}\)

Notación decimal	Notación Científica
\(\ 0.05\)	\(\ 5 \times 10^{-2}\)
\(\ 0.0008\)	\(\ 8 \times 10^{-4}\)
\(\ 0.00000043\)	\(\ 4.3 \times 10^{-7}\)
\(\ 0.000000000625\)	\(\ 6.25 \times 10^{-10}\)

\(\ (3 \times 6.8)\left(10^{8} \times 10^{-13}\right)\)	Reagruparse, utilizando las propiedades conmutativas y asociativas.
\(\ (20.4)\left(10^{8} \times 10^{-13}\right)\)	Multiplicar los coeficientes.
\(\ 20.4 \times 10^{-5}\)	Multiplica las potencias de 10 usando la Regla del Producto: sumar los exponentes.
\(\ \left(2.04 \times 10^{1}\right) \times 10^{-5}\)	Convierte 20.4 en notación científica moviendo el punto decimal un lugar hacia la izquierda y multiplicando por 10 ¹.
\(\ 2.04 \times\left(10^{1} \times 10^{-5}\right)\)	Agrupar las potencias de 10 utilizando la propiedad asociativa de la multiplicación.
\(\ 2.04 \times 10^{1+(-5)}\)	Multiplicar usando la Regla del Producto: sumar los exponentes.

\(\ (8.2 \times1.5\times1.9)(10^6\times10^{-3}\times10^{-7})\)	Reagruparse, utilizando las propiedades conmutativas y asociativas.
\(\ (23.37)\left(10^{6} \times 10^{-3} \times 10^{-7}\right)\)	Multiplique los números.
\(\ 23.37 \times 10^{-4}\)	Multiplica las potencias de 10 usando la Regla del Producto: sumar los exponentes.
\(\ \left(2.337 \times 10^{1}\right) \times 10^{-4}\)	Convierte 23.37 en notación científica moviendo el punto decimal un lugar hacia la izquierda y multiplicando por 10 ¹.
\(\ 2.337 \times\left(10^{1} \times 10^{-4}\right)\)	Agrupar las potencias de 10 utilizando la propiedad asociativa de la multiplicación.
\(\ 2.337 \times 10^{1+(-4)}\)	Multiplica usando la Regla del Producto y agrega los exponentes.

\(\ \left(\frac{2.829}{3.45}\right)\left(\frac{10^{-9}}{10^{-3}}\right)\)	Reagruparse, utilizando la propiedad asociativa.
\(\ (0.82)\left(\frac{10^{-9}}{10^{-3}}\right)\)	Dividir los coeficientes.
\ (\\ begin {array} {c} 0.82\ times 10^ {-9- (-3)}\\ 0.82\ times 10^ {-6} \ end {array}\)	Dividir los poderes de 10 usando la Regla del Cociente: restar los exponentes.
\(\ \left(8.2 \times 10^{-1}\right) \times 10^{-6}\)	Convierte 0.82 en notación científica moviendo el punto decimal un lugar a la derecha y multiplicando por 10 ^-1.
\(\ 8.2 \times\left(10^{-1} \times 10^{-6}\right)\)	Agrupar los poderes de 10 juntos usando la propiedad asociativa.
\(\ 8.2 \times 10^{-1+(-6)}\)	Multiplica las potencias de 10 usando la Regla del Producto: sumar los exponentes.

\(\ \frac{(1.37 \times 9.85)\left(10^{6} \times 10^{4}\right)}{5.0 \times 10^{12}}\)	Reagrupar los términos en el numerador según las propiedades asociativas y conmutativas.
\(\ \frac{13.4945 \times 10^{10}}{5.0 \times 10^{12}}\)	Multiplicar.
\(\ \left(\frac{13.4945}{5.0}\right)\left(\frac{10^{10}}{10^{12}}\right)\)	Reagruparse, utilizando la propiedad asociativa.
\(\ (2.6989)\left(\frac{10^{10}}{10^{12}}\right)\)	Dividir los números.
\ (\\ begin {array} {r} (2.6989)\ left (10^ {10-12}\ derecha)\\ 2.6989\ times 10^ {-2} \ end {array}\)	Dividir los poderes de 10 usando la Regla del Cociente: restar los exponentes.