11.2.1: Introducción a los polinomios de una sola variable

Objetivos de aprendizaje

• Identificar los términos, los coeficientes y los exponentes de un polinomio.
• Evaluar un polinomio para valores dados de la variable.
• Simplifique los polinomios recopilando términos similares.

Introducción

Las expresiones algebraicas se crean combinando números y variables usando operaciones aritméticas: suma, resta, multiplicación, división y exponenciación. Usando todos menos la división, puede crear una expresión llamada polinomio agregando o restando términos. Los polinomios son muy útiles en aplicaciones desde la ciencia y la ingeniería hasta los negocios. Los monomios (y polinomios en general) pueden tener más de una variable, pero en esta unidad, solo trabajarás con polinomios de una sola variable.

Monomios

El bloque básico de construcción de un polinomio es un monomio. Un monomio es un término y puede ser un número, una variable o el producto de un número y variables con un exponente. A la parte numérica del término se le llama coeficiente.

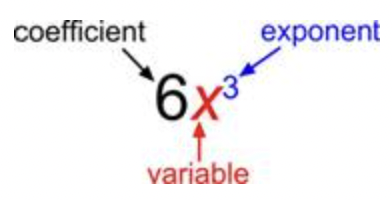
El coeficiente puede ser cualquier número real, incluyendo 0. El exponente de la variable debe ser un número entero: 0, 1, 2, 3, y así sucesivamente. Un monomio no puede tener una variable en el denominador o un exponente negativo.

El valor del exponente es el grado del monomio. Recuerda que una variable que parece no tener exponente realmente tiene un exponente de 1. Y un monomio sin variable tiene un grado de 0. (\(\ x^{0} \)tiene el valor de 1 si\(\ x \neq 0\). Entonces un número como 3 podría escribirse como\(\ 3 x^{0}\), si\(\ x \neq 0\). Cuando\(\ x \neq 0\) se puede escribir como\(\ 3 x^{0}=3 \cdot 1=3\).)

Ejemplo

Identificar el coeficiente, la variable y el exponente del monomio\(\ \frac{3}{5} k^{8}\).

Solución

La variable es\(\ k\).

El exponente de\(\ k\) es 8.

El coeficiente de\(\ k^{8}\) es\(\ \frac{3}{5}\).

Ejemplo

Identificar el coeficiente, variable y exponente de\(\ x\).

Solución

El exponente de\(\ x\) es 1.	\(\ x=x^{1}\), por lo que el exponente es 1.
El coeficiente de\(\ x\) es 1.	\(\ x=1 x^{1}\)por lo que el coeficiente también es 1.

La variable es\(\ x\).

Ejercicio

Identificar el coeficiente, variable y exponente de\(\ 3y\).

1. La variable es\(\ y\), el exponente es 3, y el coeficiente es 1.
2. La variable es\(\ y\), el exponente es 0 y el coeficiente es 3.
3. La variable es\(\ y\), el exponente es 1 y el coeficiente es 3.
4. La variable es\(\ y\), el exponente es 3, y el monomio no tiene coeficiente.

Contestar

1. La variable es\(\ y\), el exponente es 3, y el coeficiente es 1.

   Incorrecto. El exponente es la potencia de la variable y el coeficiente es el número antes de la variable. El coeficiente en este caso es 3, y el exponente es 1 porque\(\ 3 y=3 y^{1}\).

2. La variable es\(\ y\), el exponente es 0 y el coeficiente es 3.

   Incorrecto. El coeficiente es 3, pero el exponente es 1 porque\(\ 3 y=3 y^{1}\). Un exponente de 0 sería\(\ 3 y^{0}\), y desde\(\ y^{0}=1\) cuándo\(\ y \neq 0\), esto sería igual a 3 (cuándo\(\ y \neq 0\)).

3. La variable es\(\ y\), el exponente es 1 y el coeficiente es 3.

   Correcto. El coeficiente es 3, la variable es\(\ y\), y el exponente es 1 porque\(\ 3 y=3 y^{1}\).

4. La variable es\(\ y\), el exponente es 3, y el monomio no tiene coeficiente.

   Incorrecto. El exponente es la potencia de la variable y el coeficiente es el número antes de la variable. El coeficiente en este caso es 3, y el exponente es 1 porque\(\ 3 y=3 y^{1}\).

Nombrar y escribir polinomios

Un polinomio es un monomio o la suma o diferencia de dos o más polinomios. A cada monomio se le llama término del polinomio.

Algunos polinomios tienen nombres específicos indicados por su prefijo.

monomial - es un polinomio con exactamente un término (“mono” - significa uno)

binomio - es un polinomio con exactamente dos términos (“bi” - significa dos)

trinomio - es un polinomio con exactamente tres términos (“tri” - significa tres)

La palabra “polinomio” tiene el prefijo, “poli”, que significa muchos. Sin embargo, la palabra polinomio se puede utilizar para todos los números de términos, incluyendo solo un término.

Debido a que el exponente de la variable debe ser un número entero, los monomios y polinomios no pueden tener una variable en el denominador.

Los polinomios se pueden clasificar por el grado del polinomio. El grado de un polinomio es el grado de su término de grado más alto. Entonces el grado de\(\ 2 x^{3}+3 x^{2}+8 x+5\) es 3.

Se dice que un polinomio está escrito en forma estándar cuando los términos se organizan desde el grado más alto hasta el grado más bajo. Cuando se escribe en forma estándar, es fácil determinar el grado del polinomio.

Las tablas siguientes ilustran algunos ejemplos de monomios, binomios, trinomios y otros polinomios. Todos están escritos en forma estándar.

Monomios

15

\(\ \frac{1}{2} x\)

\(\ -4 y^{3}\)

\(\ 16 n^{4}\)

Binomios

\(\ 3 y+13\)

\(\ 4 p-7\)

\(\ 3 x^{2}+\frac{5}{8} x\)

\(\ 14 y^{3}+3 y\)

Trinomios

\(\ x^{3}-x^{2}+1\)

\(\ 3 x^{2}+2 x-9\)

\(\ 3 y^{3}+y^{2}-2\)

\(\ a^{7}+2 a^{5}-3 a^{3}\)

Otros polinomios

\(\ 5 x^{4}+3 x^{3}-6 x^{2}+2 x\)

\(\ \frac{1}{3} x^{5}-2 x^{4}+\frac{2}{9} x^{3}-x^{2}+4 x-\frac{5}{6}\)

\(\ 3 t^{3}-3 t^{2}-3 t-3\)

\(\ q^{7}+2 q^{5}-3 q^{3}+q\)

Cuando el coeficiente de un término polinomio es 0, normalmente no escribes el término en absoluto (porque 0 veces algo es 0, y agregar 0 no cambia el valor). El último binomio en la tabla binomial\(\ 14 y^{3}+3 y\),, podría escribirse como trinomio,\(\ 14 y^{3}+0 y^{2}+3 y\).

Un término sin una variable se llama término constante, y el grado de ese término es 0. Por ejemplo 13 es el término constante en\(\ 3 y+13\). Normalmente dirías que no\(\ 14 y^{3}+3 y\) tiene término constante o que el término constante es 0.

Ejercicio

¿Cuáles de las siguientes expresiones son polinomios?

\(\ 2 x^{4}-3 x^{3}\)

\(\ 14\)

\(\ \frac{x+1}{x}\)

1. Sólo\(\ 2 x^{4}-3 x^{3}\) y\(\ \frac{x+1}{x}\) son polinomios.
2. Sólo\(\ 2 x^{4}-3 x^{3}\) y 14 son polinomios.
3. Sólo\(\ 2 x^{4}-3 x^{3}\) es un polinomio.
4. Ninguna de las expresiones es un polinomio.

Contestar

1. Sólo\(\ 2 x^{4}-3 x^{3}\) y\(\ \frac{x+1}{x}\) son polinomios.

   Incorrecto. \(\ \frac{x+1}{x}\)no es un polinomio porque tiene una variable en el denominador. La respuesta correcta es\(\ 2 x^{4}-3 x^{3}\) y 14.

2. Sólo\(\ 2 x^{4}-3 x^{3}\) y 14 son polinomios.

   Correcto. \(\ \frac{x+1}{x}\)no es un polinomio porque tiene una variable en el denominador.

3. Sólo\(\ 2 x^{4}-3 x^{3}\) es un polinomio.

   Incorrecto. 14 también es un monomio, un tipo de polinomio. La respuesta correcta es\(\ 2 x^{4}-3 x^{3}\) y 14.

4. Ninguna de las expresiones es un polinomio.

   Incorrecto. \(\ x^{4}-3 y^{3}\)y 14 son polinomios. \(\ \frac{x+1}{x}\)no es un polinomio porque tiene una variable en el denominador.

Evaluación de polinomios

Puedes evaluar polinomios tal como has estado evaluando expresiones todo el tiempo. Para evaluar una expresión por un valor de la variable, se sustituye el valor por la variable cada vez que aparece. A continuación, utilice el orden de las operaciones para encontrar el valor resultante para la expresión.

Ejemplo

Evaluar\(\ 3 x^{2}-2 x+1\) y\(\ x=-1\).

Solución

\(\ 3(-1)^{2}-2(-1)+1\)	Sustituye -1 por cada uno\(\ x\) en el polinomio.
\(\ 3(1)-2(-1)+1\)	Siguiendo el orden de las operaciones, evaluar primero a los exponentes.
\(\ 3+(-2)(-1)+1\)	Multiplicar 3 veces 1, y luego multiplicar -2 veces -1.
\(\ 3+2+1\)	Cambiar la resta a suma de lo contrario.
\(\ 3 x^{2}-2 x+1=6, \text { for } x=-1\)	Encuentra la suma.

Ejemplo

Evaluar\(\ -\frac{2}{3} p^{4}+2 p^{3}-p\) para\(\ p=3\)

Solución

\(\ -\frac{2}{3}(3)^{4}+2(3)^{3}-3\)	Sustituye 3 por cada uno\(\ p\) en el polinomio.
\(\ -\frac{2}{3}(81)+2(27)-3\)	Siguiendo el orden de las operaciones, evalúe primero los exponentes y luego multiplique.
\(\ -54+54-3\)	Sumar y después restar para obtener -3.

\(\ -\frac{2}{3} p^{4}+2 p^{3}-p=-3, \text { for } p=3\)

Ejercicio

Evaluar\(\ 3 x^{3}-2 x^{2} \text { for } x=-2\).

1. \(\ -24-2 x^{2}\)
2. \(\ -32\)
3. \(\ -16\)
4. \(\ 16\)

Contestar

1. \(\ -24-2 x^{2}\)

   Incorrecto. \(\ x=-2\)para todas las apariencias de\(\ x\) en la expresión. Debe sustituir -2 en ambas instancias:\(\ 3(-2)^{3}-2(-2)^{2}\). La respuesta correcta es -32.

2. \(\ -32\)

   Correcto. Desde\(\ x=-2\):\(\ 3 x^{3}-2 x^{2}=3(-2)^{3}-2(-2)^{2}=3(-8)-2(4)=-24-8=-32\).

3. \(\ -16\)

   Incorrecto. Es posible que hayas olvidado que\(\ (-2)^{2}\) es positivo, o has cometido otro error en tus cálculos. Desde\(\ x=-2\):\(\ 3 x^{3}-2 x^{2}=3(-2)^{3}-2(-2)^{2}=3(-8)-2(4)=-24-8=-32\).

4. \(\ 16\)

   Incorrecto. Puede que hayas olvidado que\(\ (-2)^{3}\) es negativo (el producto de dos valores negativos es positivo, por lo que multiplicar por un tercer negativo da un producto negativo). Desde\(\ x=-2\):\(\ 3 x^{3}-2 x^{2}=3(-2)^{3}-2(-2)^{2}=3(-8)-2(4)=-24-8=-32\).

Simplificación de polinomios

Un polinomio puede necesitar ser simplificado. Una forma de simplificar un polinomio es combinar los términos similares si los hay. Dos o más términos en un polinomio son como términos si tienen la misma variable (o variables) con el mismo exponente. Por ejemplo,\(\ 3 x^{2}\) y\(\ -5 x^{2}\) son como términos: Ambos tienen\(\ x\) como variable, y el exponente es 2 para cada uno. Sin embargo,\(\ 3 x^{2}\) y no\(\ 3x\) son como términos, porque sus exponentes son diferentes.

Aquí hay algunos ejemplos de términos que son como y algunos que son diferentes.

Monomios	Términos	Explicación
\ (\\ begin {array} {l} 3 x\\ 14 x \ end {array}\)	como	mismas variables con los mismos exponentes
\ (\\ begin {array} {l} 16 z^ {2}\\ -5 z^ {2} \ end {array}\)	como	mismas variables con los mismos exponentes
\ (\\ begin {array} {l} 3x\\ 5y \ end {array}\)	a diferencia de	diferentes variables (aunque los mismos exponentes)
\ (\\ begin {array} {l} -3z\\ -3z^2 \ end {array}\)	a diferencia de	mismas variables pero con diferentes exponentes

Ejemplo

¿Cuáles de estos términos son como términos?

\(\ 7 x^{3}, 7 x, 7 y,-8 x^{3}, 9 y,-3 x^{2}, 8 y^{2}\)

Solución

\ (\\ begin {array} {l} x: 7 x^ {3}, 7 x, -8 x^ {3}, -3 x^ {2}\\ y: 7 y, 9 y, 8 y^ {2} \ end {array}\)	Los términos similares deben tener las mismas variables, así que primero identifique qué términos usan las mismas variables.
Los\(\ x\) términos\(\ 7 x^{3}\) y\(\ -8 x^{3}\) tienen el mismo exponente. él\(\ y\) términos\(\ 7 y\) y\(\ 9 y\) tienen el mismo exponente.	Los términos similares también deben tener los mismos exponentes. Identificar qué términos con las mismas variables también usan los mismos exponentes.

\(\ 7 x^{3}\)y\(\ -8 x^{3}\) son como términos.

\(\ 7 y\)y\(\ 9 y\) son como términos.

Ejercicio

¿Cuáles de estos son como términos?

\(\ -3 a, 3 a^{2}, 8 b,-3 b^{3}, 8 a, 14 b^{2}, 9 a\)

1. Sólo\(\ -3 a\),\(\ 8 a\), y\(\ 9a\) son como términos.
2. Sólo\(\ 8a\) y\(\ 9a\) son como términos.
3. \(\ 8b\),\(\ -3 b^{3}\), y\(\ 14 b^{2}\) son términos similares, y\(\ -3 a\),\(\ 3 a^{2}\),\(\ 8 a\), y\(\ 9a\) son términos similares.
4. \(\ 3 a^{2}\)y\(\ 14 b^{2}\) son términos similares, y\(\ -3 a\),\(\ 8 b\),\(\ 8a\), y\(\ 9a\) son términos similares.

Contestar

1. Sólo\(\ -3 a\),\(\ 8 a\), y\(\ 9a\) son como términos.

   Correcto. Estos términos tienen la misma variable,\(\ a\), con un exponente de 1.

2. Sólo\(\ 8a\) y\(\ 9a\) son como términos.

   Incorrecto. \(\ -3 a\)también es un término similar con\(\ 8a\) y\(\ 9 a\), porque tiene la misma variable con el mismo exponente.

3. \(\ 8b\),\(\ -3 b^{3}\), y\(\ 14 b^{2}\) son términos similares, y\(\ -3 a\),\(\ 3 a^{2}\),\(\ 8 a\), y\(\ 9a\) son términos similares.

   Incorrecto. Cada grupo tiene la misma variable, pero sus exponentes son diferentes. Los únicos términos con la misma variable y exponente son\(\ -3 a\),\(\ 8 a\), y\(\ 9 a\).

4. \(\ 3 a^{2}\)y\(\ 14 b^{2}\) son términos similares, y\(\ -3 a\),\(\ 8 b\),\(\ 8a\), y\(\ 9a\) son términos similares.

   Incorrecto. Cada grupo tiene el mismo exponente, pero sus variables son distintas. Los únicos términos con la misma variable y exponente son\(\ -3 a\),\(\ 8 a\), y\(\ 9a\).

Puede utilizar la propiedad distributiva para simplificar la suma de términos similares. Recordemos que la propiedad distributiva de suma establece que el producto de un número y una suma (o diferencia) es igual a la suma (o diferencia) de los productos.

\(\ 2(3+6)=2(3)+2(6)\)

Ambas expresiones equivalen a 18. Para que puedas escribir la expresión en la forma que sea más útil.

Veamos cómo podemos usar esta propiedad para combinar términos similares.

Ejemplo

Simplificar\(\ 3 x^{2}-5 x^{2}\).

Solución

\(\ 3\left(x^{2}\right)-5\left(x^{2}\right)\)	\(\ 3 x^{2}\)y\(\ 5 x^{2}\) son como términos.
\(\ (3-5)\left(x^{2}\right)\)	Podemos reescribir la expresión como producto de la diferencia.
\(\ (-2)\left(x^{2}\right)\)	Calcular\(\ 3-5\).
\(\ 3 x^{2}-5 x^{2}=-2 x^{2}\)	Escribe la diferencia de\(\ 3-5\) como el nuevo coeficiente.

Es posible que hayas notado que combinar términos similares implica combinar los coeficientes para encontrar el nuevo coeficiente del término similar. Puedes usar esto como atajo.

Ejemplo

Simplificar\(\ 6 a^{4}+4 a^{4}\).

Solución

\(\ 6 a^{4}+4 a^{4}\)	Observe que ambos términos tienen un número multiplicado por\(\ a^{4}\). Esto los hace como términos.
\(\ (6+4)\left(a^{4}\right)\)	Combinar los coeficientes, 6 y 4.
\(\ (10)\left(a^{4}\right)\)	Calcular la suma.
\(\ 6 a^{4}+4 a^{4}=10 a^{4}\)	Escribe la suma como el nuevo coeficiente.

Cuando se tiene un polinomio con más términos, hay que tener cuidado de combinar sólo como términos. Si dos términos no son como términos, no puedes combinarlos.

Ejemplo

Simplificar\(\ 3 x^{2}+3 x+x+1+5 x\).

Solución

\(\ 3x\),\(\ x\), y\(\ 5x\) son como términos	Primero identifique qué términos son como términos: only\(\ 3x\),\(\ x\), and\(\ 5x\) are like terms.
\(\ 3 x^{2}+3 x+x+1+5 x=3 x^{2}+(3 x+x+5 x)+1\)	Utilice las propiedades conmutativa y asociativa para agrupar los términos similares.
\(\ 3 x^{2}+(3+1+5) x+1\)	Sumar los coeficientes de los términos similares. Recuerda que el coeficiente de\(\ x\) es 1 porque\(\ x=1 x\).
\(\ 3 x^{2}+(9) x+1\)
\(\ 3 x^{2}+3 x+x+1+5 x=3 x^{2}+9 x+1\)	Escribe la suma como el nuevo coeficiente.

Ejercicio

Simplifica combinando términos similares.

\(\ -3 a+3 a^{2}+8 a+9 a-3\)

1. \(\ 3 a^{2}+17 a-3\)
2. \(\ 3 a^{2}+14 a-3\)
3. \(\ 17 a-3\)
4. \(\ 17 a-3 a-3\)

Contestar

1. Incorrecto. Hay tres términos con\(\ a\) (recuerda que\(\ a^{1}\)) se escribe como\(\ a\)):\(\ -3 a\),\(\ 8a\), y\(\ 9a\). Combinarlos da\(\ -3 a+8 a+9 a=(-3+8+9) a=14 a\), así lo es el polinomio simplificado\(\ 3 a^{2}+14 a-3\).
2. Correcto. Hay tres términos con\(\ a\) (recuerda que\(\ a^{1}\) está escrito como\(\ a\)):\(\ -3a\),\(\ 8a\), y\(\ 9a\). Combinarlos da\(\ -3 a+8 a+9 a=(-3+8+9) a=14 a\), así lo es el polinomio simplificado\(\ 3 a^{2}+14 a-3\).
3. Incorrecto. Es posible que haya combinado incorrectamente los dos primeros términos,\(\ -3 a+3 a^{2}\). Estos no son como términos, así que no puedes combinarlos. Hay tres términos con\(\ a\) (recuerda que\(\ a^{1}\) está escrito como\(\ a\)):\(\ -3a\),\(\ 8a\), y\(\ 9a\). Combinarlos da\(\ -3 a+8 a+9 a=(-3+8+9) a=14 a\), así lo es el polinomio simplificado\(\ 3 a^{2}+14 a-3\).
4. Incorrecto. Hay tres términos con\(\ a\) (recuerda que\(\ a^{1}\) está escrito como\(\ a\)):\(\ -3a\),\(\ 8a\), y\(\ 9a\). Combinarlos da\(\ -3 a+8 a+9 a=(-3+8+9) a=14 a\), así lo es el polinomio simplificado\(\ 3 a^{2}+14 a-3\).

Resumen

Los polinomios son expresiones algebraicas que contienen cualquier número de términos combinados usando suma o resta. Un término es un número, una variable o un producto de un número y una o más variables con exponentes. Se pueden combinar términos similares (misma variable o variables elevadas a la misma potencia) para simplificar un polinomio. Los polinomios se pueden evaluar sustituyendo un valor dado de la variable en cada instancia de la variable, luego usando orden de operaciones para completar los cálculos.