13.1.2: Graficar ecuaciones lineales

Última actualización
Guardar como PDF

Page ID: 111538

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Utilice pares de coordenadas para graficar relaciones lineales.
Grafique una ecuación lineal usando intercepciones x e y.
Determinar si un par ordenado es una solución de una ecuación.
Resolver problemas de aplicación que involucran gráficas de ecuaciones lineales.

Introducción

Graficar pares ordenados es solo el comienzo de la historia. Una vez que sabes cómo colocar puntos en una cuadrícula, puedes usarlos para dar sentido a todo tipo de relaciones matemáticas.

Puede utilizar un plano de coordenadas para trazar puntos y mapear diversas relaciones, como la relación entre la distancia de un objeto y el tiempo transcurrido. Muchas relaciones matemáticas son relaciones lineales. Veamos qué es una relación lineal.

Relaciones Lineales

Una relación lineal es una relación entre variables tal que cuando se trazan en un plano de coordenadas, los puntos se encuentran en una línea. Empecemos por mirar una serie de puntos en el Cuadrante I en el plano de coordenadas.

Mira los cinco pares ordenados (y sus coordenadas x e y) a continuación. ¿Ves algún patrón a la ubicación de los puntos? Si este patrón continuara, ¿qué otros puntos podrían estar en la línea?

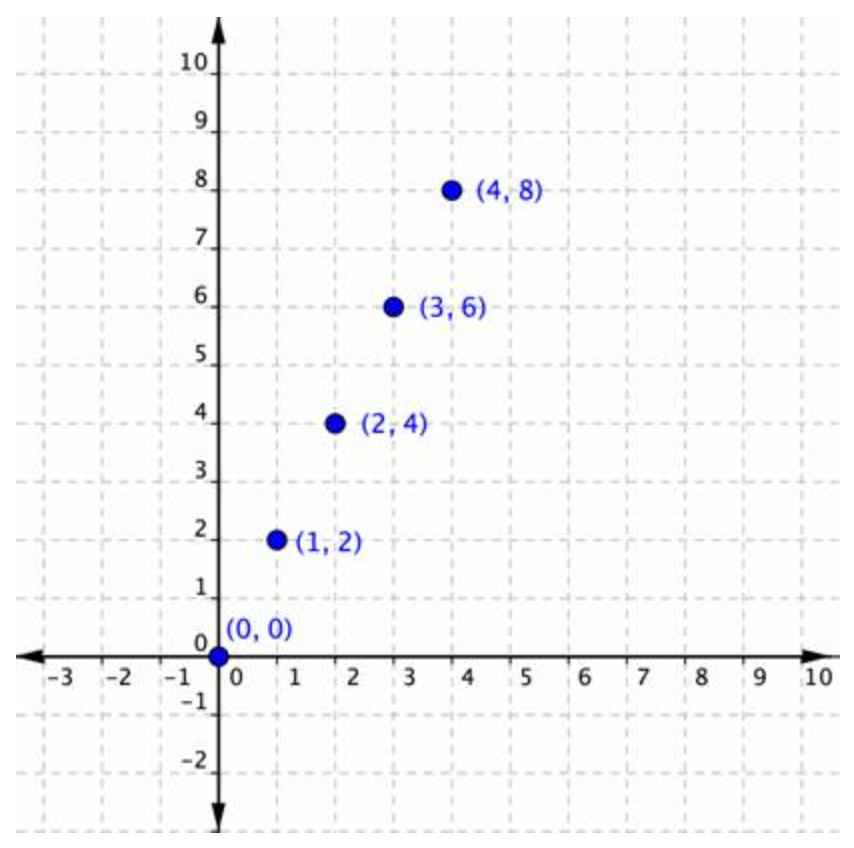
$Screen Shot 2021-06-24 a las 10.45.54 AM.png$

Probablemente identificaste que si este patrón continuaba, el siguiente par ordenado estaría en (5, 10). Esto tiene sentido porque el punto. (5, 10) “alinea” con los otros puntos de la serie —está literalmente en la misma línea que los demás. Aplicando la misma lógica, puede identificar que los pares ordenados (6, 12) y (7, 14) también pertenecerían si este plano de coordenadas fuera más grande; ellos, también, se alinearán con los otros puntos.

Estas series de puntos también se pueden representar en una tabla. En la siguiente tabla se registran las coordenadas x e y de cada par ordenado en la gráfica.

coordenada x	coordenada y
0	0
1	2
2	4
3	6
4	8
5	10
6	12
7	14

Observe que cada coordenada y es el doble del valor x correspondiente. Todos estos valores x e y siguen el mismo patrón y, cuando se colocan en un plano de coordenadas, todos se alinean.

Una vez que conozca el patrón que relaciona los valores x e y, puede encontrar un valor y para cualquier valor x que se encuentre en la línea. Entonces, si la regla de este patrón es que cada coordenada y es el doble del valor x correspondiente, entonces los pares ordenados (1.5, 3), (2.5, 5) y (3.5, 7) deberían aparecer todos en la línea también, ¿correcto? Mira para ver qué pasa.

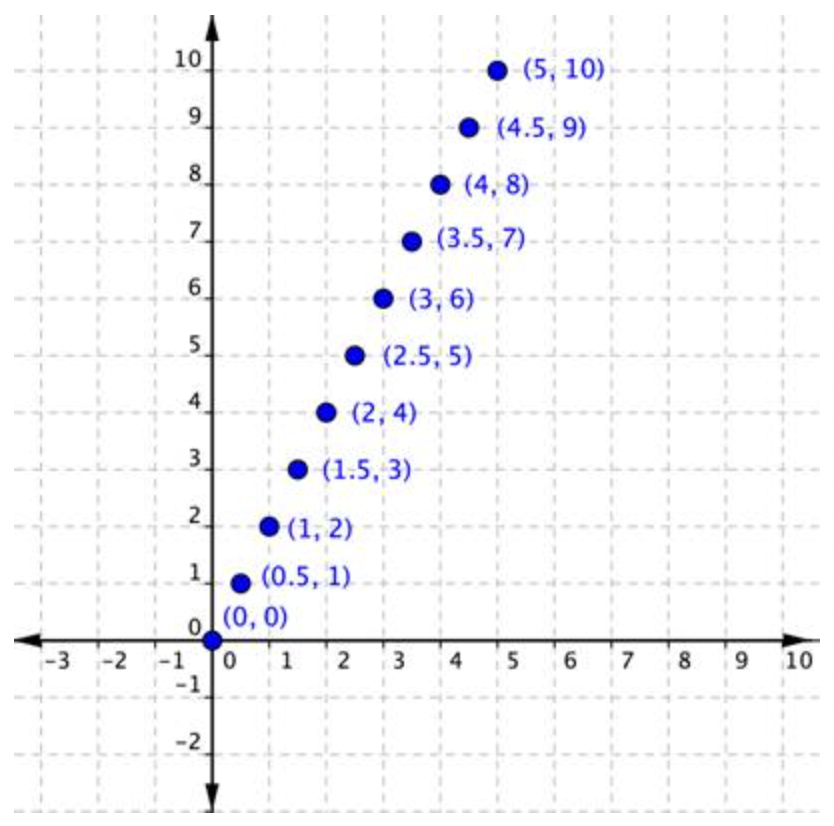
$Screen Shot 2021-06-24 at 11.02.42 AM.png$

Si tuvieras que seguir sumando pares ordenados (x, y) donde el valor y era el doble del valor x, terminarías con una gráfica como esta.

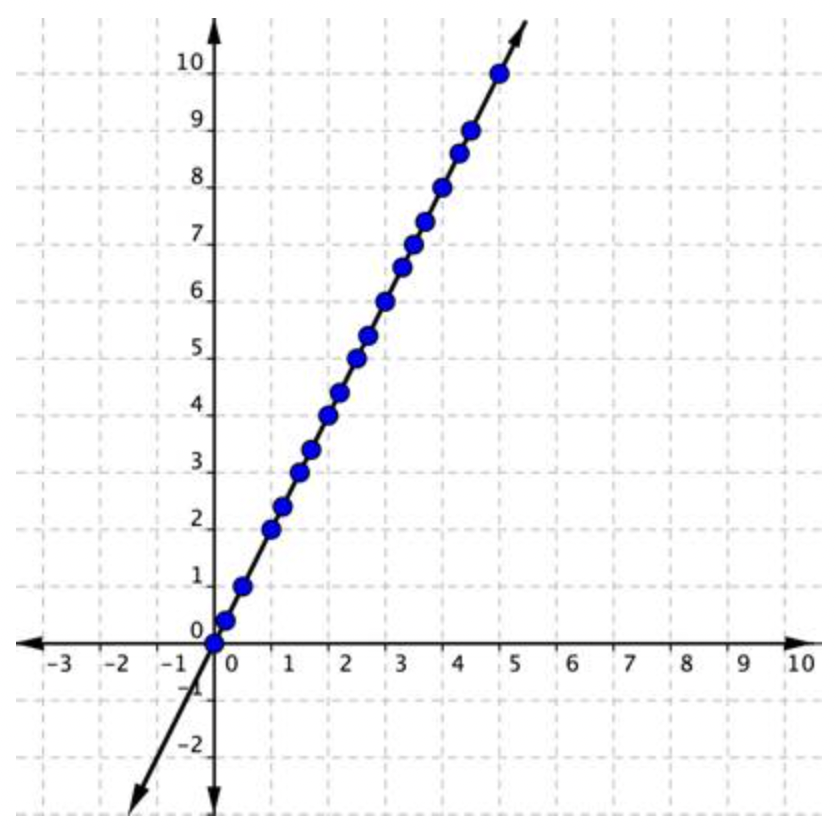
$Screen Shot 2021-06-24 at 11.06.15 AM.png$

Mira cómo todos los puntos se mezclan para crear una línea. Se puede pensar en una línea, entonces, como una colección de un número infinito de puntos individuales que comparten la misma relación matemática. En este caso, la relación es que el valor y es el doble del valor x.

Hay múltiples formas de representar una relación lineal: una tabla, una gráfica lineal y también hay una ecuación lineal. Una ecuación lineal es una ecuación con dos variables cuyos pares ordenados se grafican como una línea recta.

Hay varias formas de crear una gráfica a partir de una ecuación lineal. Una forma es crear una tabla de valores para x e y, a continuación, trazar estos pares ordenados en el plano de coordenadas. Dos puntos son suficientes para determinar una línea. No obstante, siempre es buena idea trazar más de dos puntos para evitar posibles errores.

Después dibujas una línea a través de los puntos para mostrar todos los puntos que están en la línea. Las flechas en cada extremo de la gráfica indican que la línea continúa sin cesar en ambas direcciones. Cada punto de esta línea es una solución a la ecuación lineal.

Ejemplo

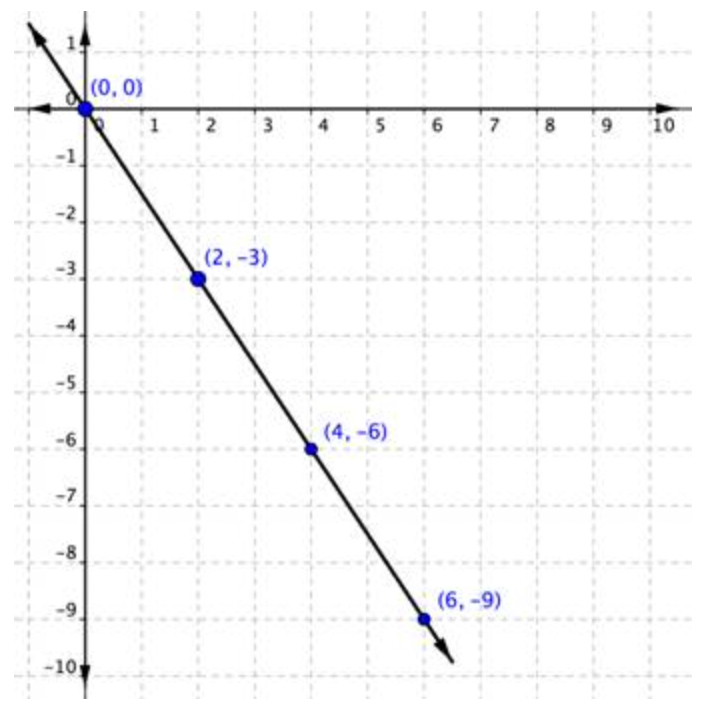
Grafica la ecuación lineal$\ y=-1.5 x$.

Solución

$\ x$valores	$\ -1.5 x$	$\ y$valores
0	-1.5 (0)	0
2	-1.5 (2)	-3
4	-1.5 (4)	-6
6	-1.5 (6)	-9

Evaluar$\ y=-1.5 x$ para diferentes valores de$\ x$, y crear una tabla de$\ y$ valores correspondientes$\ x$ y.

Dado que el coeficiente de$\ x$ es -1.5, es conveniente elegir múltiplos de 2 para$\ x$. Esto asegura que$\ y$ sea un entero, y hace que la línea sea más fácil de graficar.

Convertir la tabla en pares ordenados. Después, trazar los pares ordenados.

\ (\\ begin {array} {c}
(0,0)\\
(2, -3)\\
(4, -6)\\
(6, -9)
\ end {array}\)

Dibuja una línea a través de los puntos para indicar todos los puntos de la línea.

$Screen Shot 2021-06-24 a las 11.15.58 AM.png$

Ejemplo

Grafica la ecuación lineal$\ y=2 x+3$.

Solución

$\ x$valores	$\ 2 x+3$	$\ y$valores
0	2 (0) +3	3
1	2 (1) +3	5
2	2 (2) +3	7
3	2 (3) +3	9

Evaluar$\ y=2 x+3$ para diferentes valores de$\ x$, y crear una tabla de$\ y$ valores correspondientes$\ x$ y.

\ (\\ begin {array} {l}
(0,3)\\
(1,5)\\
(2,7)\\
(3,9)
\ end {array}\)

Convertir la tabla en pares ordenados.

Trazar los pares ordenados (se muestran a continuación).

Dibuja una línea a través de los puntos para indicar todos los puntos de la línea.

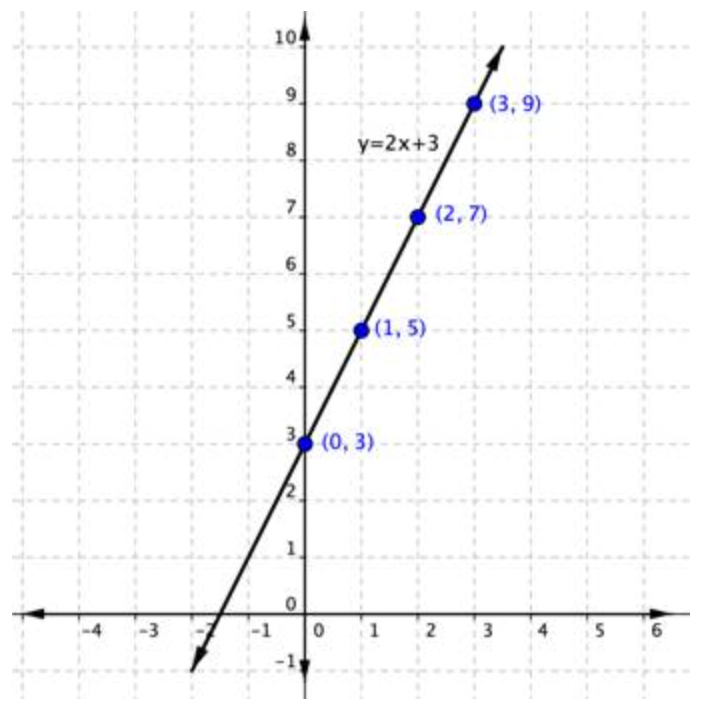
$Screen Shot 2021-06-24 a las 11.21.45 AM.png$

Se resolvieron las ecuaciones lineales representadas anteriormente$\ y$. Si la ecuación no se establece en términos de$\ y$, lo mejor es resolver primero la ecuación para$\ y$. Si no hay$\ y$ en la ecuación, entonces resuelve la ecuación para$\ x$.

Ejemplo

Grafica la ecuación lineal$\ y+3 x=5$.

Solución

\ (\\ begin {array} {l}
\ text {Resolver} y+3 x=5\ texto {para} y\
y+3 x-3 x=5-3 x\
y=5-3 x
\ end {array}\)

$\ x$valores	$\ 5-3 x$	$\ y$valores
0	5-3 (0)	5
1	5-3 (1)	2
2	5-3 (2)	-1
3	5-3 (3)	-4

Evaluar$\ y=5-3 x$ para diferentes valores de$\ x$, y crear una tabla de$\ y$ valores correspondientes$\ x$ y.

\ (\\ begin {array} {c}
(0,5)\\
(1,2)\\
(2, -1)\\
(3, -4)
\ end {array}\)

Trazar los pares ordenados (se muestran a continuación).

Dibuja una línea a través de los puntos para indicar todos los puntos de la línea.

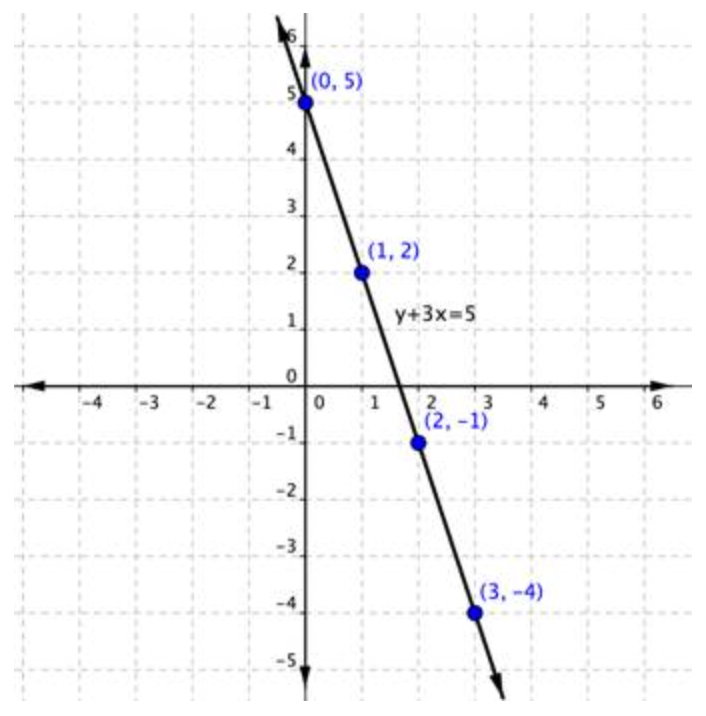
$Screen Shot 2021-06-24 a las 11.37.44 AM.png$

Las ecuaciones lineales$\ x=2$ y$\ y=-3$ sólo tienen una variable en cada una de ellas. Sin embargo, debido a que se trata de ecuaciones lineales, entonces se graficarán en un plano de coordenadas tal como lo hacen las ecuaciones lineales anteriores. Basta pensar en la ecuación$\ x=2$ como$\ x=0 y+2$ y pensar en$\ y=-3$ como$\ y=0 x-3$.

Ejemplo

Gráfica$\ y=-3$.

Solución

$\ x$valores	$\ 0 x-3$	$\ y$valores
0	0 (0) -3	-3
1	0 (1) -3	-3
2	0 (2) -3	-3
3	0 (3) -3	-3

Escribir$\ y=-3$ como$\ y=0 x-3$, y evaluar$\ y$ cuando$\ x$ tiene varios valores. O simplemente darse cuenta que$\ y=-3$ significa que cada$\ y$ valor será -3, no importa lo que$\ x$ sea.

\ (\\ begin {array} {l}
(0, -3)\\
(1, -3)\\
(2, -3)\\
(3, -3)
\ end {array}\)

Trazar los pares ordenados (se muestran a continuación).

Dibuja una línea a través de los puntos para indicar todos los puntos de la línea.

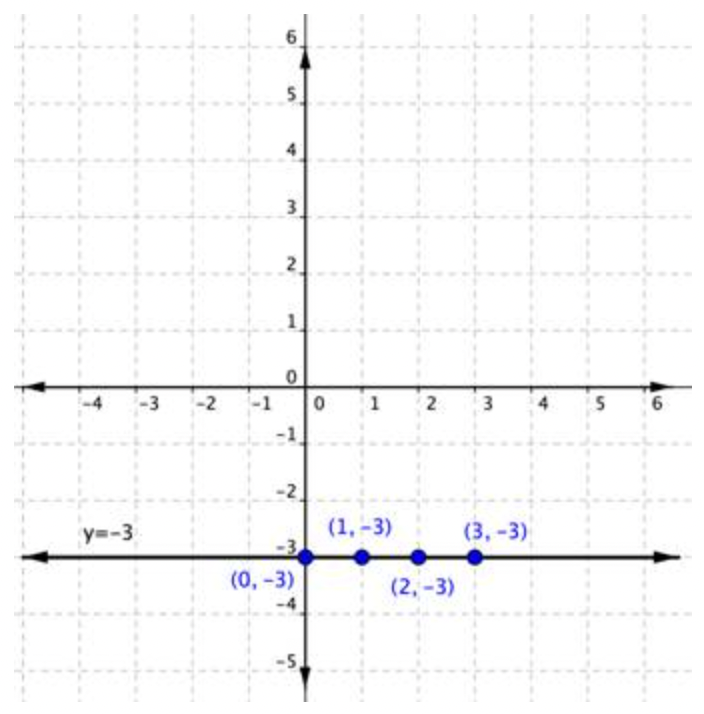
$Screen Shot 2021-06-24 a las 11.58.35 AM.png$

Observe que$\ y=-3$ grafica como una línea horizontal.

Ejercicio

¿Qué tabla de valores podría generar la ecuación$\ 2 y-5 x=10$?

$\ x$	$\ y$
5	0
7.5	1
10	2

$\ x$	$\ y$
1	5
2	6
3	7

$\ x$	$\ y$
1	15
2	20
3	25

$\ x$	$\ y$
0	5
1	7.5
2	10

Contestar

La respuesta correcta es D. Para generar una tabla de valores para esta ecuación, primero resuelva la ecuación para$\ y$. $\ y=\frac{5}{2} x+5$

Ahora elija valores para$\ x$ y luego evalúe la ecuación para$\ y$. Cuando$\ x=0$,$\ y=5$, cuando$\ x=1$$\ y=7.5$, cuando$\ x=2$,$\ y=10$.

Intercepciones x e y

Las intercepciones de una línea son los puntos donde la línea intercepta, o cruza, los ejes horizontal y vertical. Para ayudarte a recordar lo que significa “interceptar”, piensa en la palabra “intersectar”. Las dos palabras suenan iguales y en este caso significan lo mismo.

La línea recta en la gráfica de abajo intercepta los dos ejes de coordenadas. El punto donde la línea cruza el eje x se llama intercepción x. La intersección y es el punto donde la línea cruza el eje y.

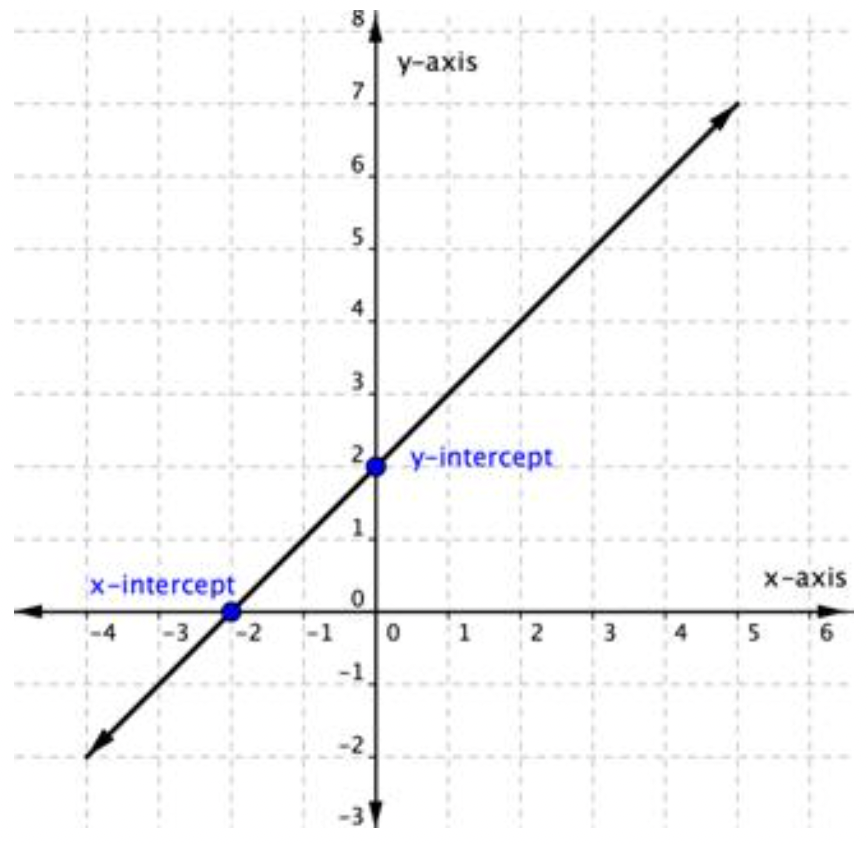
$Screen Shot 2021-06-24 a las 12.31.08 PM.png$

La intercepción x anterior es el punto (-2, 0). La intersección y anterior es el punto (0, 2).

Observe que la intercepción y siempre ocurre donde$\ x=0$, y la intercepción x siempre ocurre donde$\ y=0$.

Para encontrar las intercepciones x e y de una ecuación lineal, puede sustituir 0 por y y por x respectivamente.

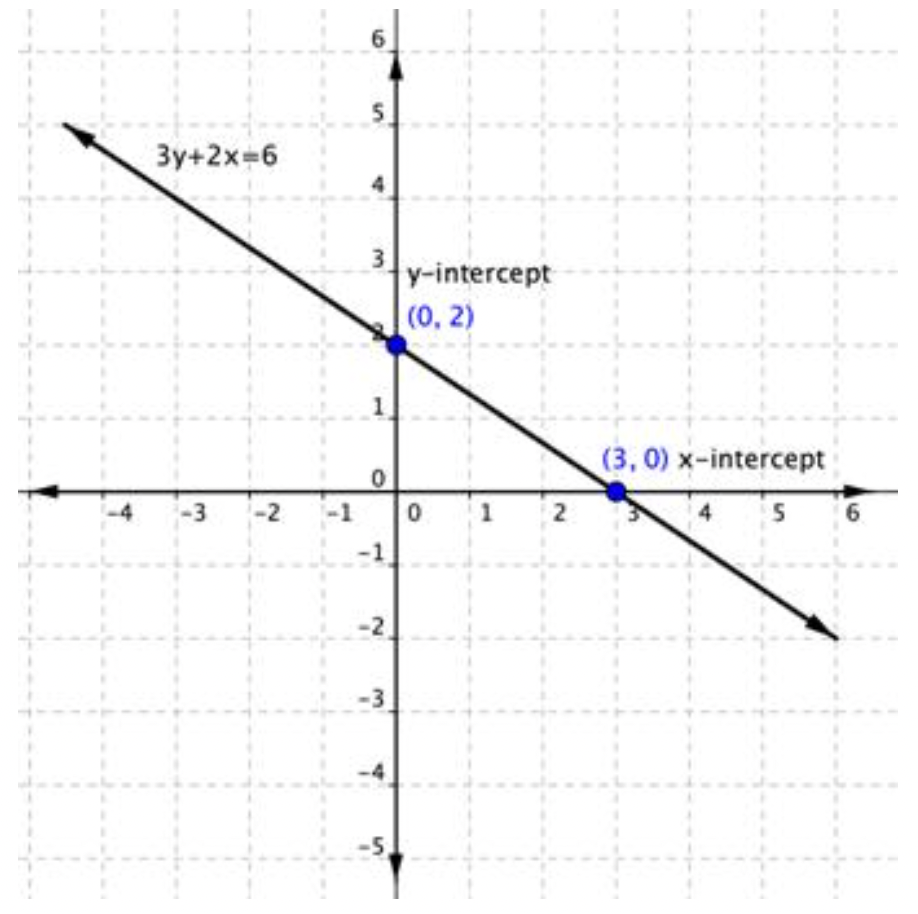
Por ejemplo, la ecuación lineal$\ 3 y+2 x=6$ tiene una$\ x$ intercepción cuando$\ y=0$, así$\ 3(0)+2 x=6$.

\ (\\ begin {array} {l}
2 x=6\
x=3
\ end {array}\)

La intercepción x es (3, 0).

De igual manera, la intersección y ocurre cuando$\ x=0$.

\ (\\ begin {array} {l}
3 y+2 (0) =6\\
3 y=6\\
y=2
\ end {array}\)

La intercepción y es (0, 2).

Ejercicio

¿Cuál es la intersección y de una línea con la ecuación$\ y=5 x-4$?

$\ \left(\frac{4}{5}, 0\right)$
$\ (-4,0)$
$\ (0,-4)$
$\ (5,-4)$

Contestar

Incorrecto. $\ \left(\frac{4}{5}, 0\right)$es la intercepción x. En la intercepción y,$\ x=0$. Cuando se sustituye 0$\ x$ en la ecuación,$\ y=-4$. La respuesta correcta es (0, -4).
Incorrecto. Esta respuesta cambia los valores de$\ x$ y$\ y$. Las coordenadas se dan en el orden$\ (x, y)$. En la intercepción y,$\ x=0$. Cuando se sustituye 0$\ x$ en la ecuación,$\ y=-4$. La respuesta correcta es$\ (0,-4)$.
Correcto. En la intercepción y,$\ x=0$. Cuando se sustituye 0$\ x$ en la ecuación,$\ y=-4$.
Incorrecto. Este es el coeficiente de$\ x$ y la constante, no la intersección y. En la intercepción y,$\ x=0$. Cuando se sustituye 0$\ x$ en la ecuación,$\ y=-4$. La respuesta correcta es$\ (0,-4)$.

Uso de intercepciones para graficar ecuaciones lineales

Puede usar intercepciones para graficar ecuaciones lineales. Una vez que hayas encontrado las dos intercepciones, dibuja una línea a través de ellas.

Hagámoslo con la ecuación$\ 3 y+2 x=6$. Descubriste que las intercepciones de la línea que representa esta ecuación son$\ (0,2)$ y$\ (3,0)$. Eso es todo lo que necesitas saber.

$Screen Shot 2021-06-24 a las 4.34.37 PM.png$

Ejemplo

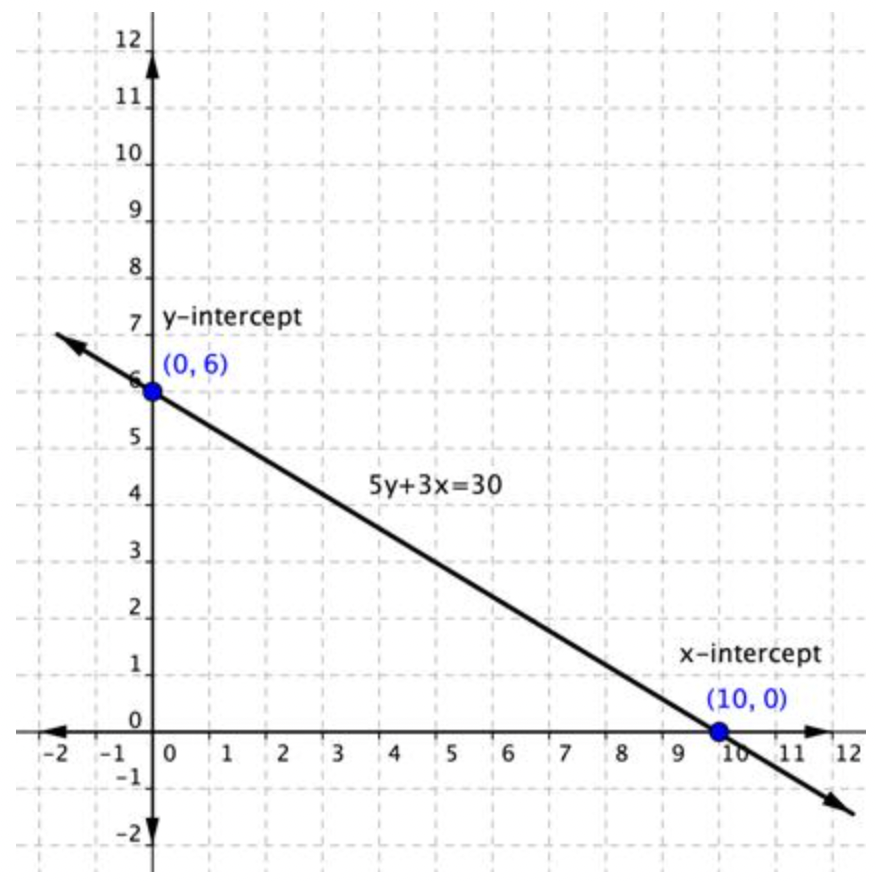
Gráfica$\ 5 y+3 x=30$.

Solución

$\ 5 y+3 x=30$

Cuando una ecuación está en$\ A x+B y=C$ forma, puede encontrar fácilmente las intercepciones x e y luego graficar.

\ (\\ begin {array} {r}
5 y+3 x=30\\
5 y+3 (0) =30\\
5 y+0=30\\
5 y=30\\ y=30\
y=6\\
y\ text {-interceptar:} (0,6)
\ end {array}\)

Para encontrar la intersección y, establecer$\ x=0$ y resolver para$\ y$.

\ (\\ begin {array} {r}
5 y+3 x =30\\
5 (0) +3 x =30\\
0+3 x =30\\
3 x =30\\
x =10\\
x\ text {-interceptar:} (10,0)
\ end {array} \)

Para encontrar la intercepción x,

establecer$\ y=0$ y resolver para$\ x$.

$Screen Shot 2021-06-24 a las 4.43.49 PM.png$

Pares ordenados como soluciones

Hasta el momento, se han considerado las siguientes ideas sobre las líneas: una línea es una representación visual de una ecuación lineal, y la línea misma está compuesta por un número infinito de puntos (o pares ordenados). La siguiente imagen muestra la línea de la ecuación lineal$\ y=2 x-5$ con algunos de los puntos específicos de la línea.

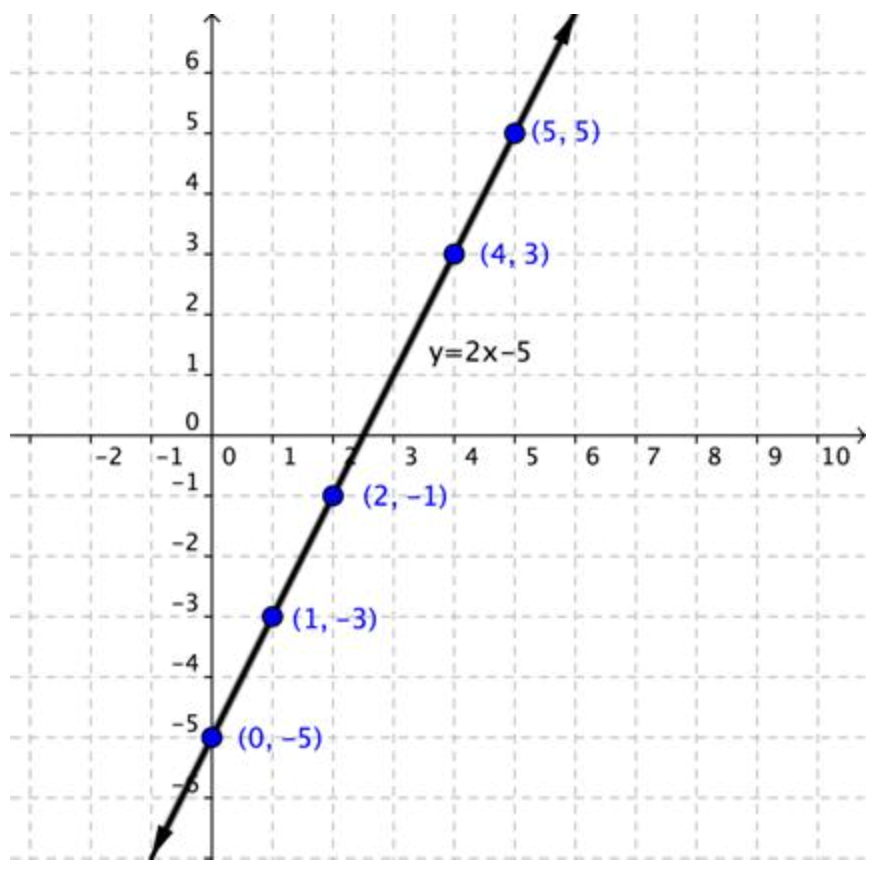
$Screen Shot 2021-06-24 a las 4.45.06 PM.png$

Cada punto de la línea es una solución a la ecuación$\ y=2 x-5$. Puedes probar cualquiera de los puntos que estén etiquetados como el par ordenado,$\ (1,-3)$.

\ (\\ begin {array} {l}
y=2 x-5\
-3=2 (1) -5\\
-3=2-5\\
-3=-3\ text {Esto es cierto.}
\ end {array}\)

También puedes probar CUALQUIERA de los otros puntos de la línea. Cada punto de la línea es una solución a la ecuación$\ y=2 x-5$. Todo esto significa que determinar si un par ordenado es una solución de una ecuación es bastante sencillo. Si el par ordenado está en la línea creada por la ecuación lineal, entonces es una solución a la ecuación. Pero si el par ordenado no está en la línea —por muy cerca que se vea— entonces no es una solución a la ecuación.

Identificación de soluciones

Para saber si un par ordenado es una solución de una ecuación lineal, puede hacer lo siguiente:

Grafica la ecuación lineal y grafica el par ordenado. Si el par ordenado parece estar en la gráfica de una línea, entonces es una posible solución de la ecuación lineal. Si el par ordenado no se encuentra en la gráfica de una línea, entonces no es una solución.
Sustituya los valores (x, y) en la ecuación. Si la ecuación produce una declaración verdadera, entonces el par ordenado es una solución de la ecuación lineal. Si el par ordenado no da una declaración verdadera, entonces no es una solución.

Ejemplo

Determinar si (-2, 4) es una solución a la ecuación$\ 4 y+5 x=3$.

Solución

\ (\\ begin {array} {r}
4 y+5 x=3\\
4 (4) +5 (-2) =3
\ end {array}\)

Para este problema, utilizará el método de sustitución. Sustituir$\ x=-2$ y$\ y=4$ en la ecuación.

\ (\\ begin {array} {r}
16+ (-10) =3\\
6=3
\ end {array}\)

Evaluar.

El enunciado no es cierto, por lo que no$\ (-2, 4)$ es una solución a la ecuación$\ 4 y+5 x=3$

$\ (-2,4)$no es una solución a la ecuación$\ 4 y+5 x=3$.

Problemas de aplicación

Las ecuaciones lineales se pueden utilizar para modelar una serie de problemas de la vida real, como la cantidad de dinero que gana con el tiempo o la distancia que recorrerá un ciclistas dada una tasa constante de pedaleo. Graficar estas relaciones en un plano de coordenadas a menudo puede ayudarte a pensar en (y encontrar soluciones) el problema.

\(\ x\)	\(\ y\)
5	0
7.5	1
10	2

\(\ x\)	\(\ y\)
1	5
2	6
3	7

\(\ x\)	\(\ y\)
1	15
2	20
3	25

\(\ x\)	\(\ y\)
0	5
1	7.5
2	10