13.1.1: El plano de coordenadas
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Trazar pares ordenados en un plano de coordenadas.
- Dado un par ordenado, determinar su cuadrante.
Introducción
El plano coordinado fue desarrollado hace siglos y refinado por el matemático francés René Descartes. En su honor, el sistema a veces se le llama el sistema de coordenadas cartesianas. El plano de coordenadas se puede utilizar para trazar puntos y trazar líneas. Este sistema nos permite describir las relaciones algebraicas en un sentido visual, y también nos ayuda a crear e interpretar conceptos algebraicos.
Conocer el plano de coordenadas
Es probable que haya usado un plano de coordenadas antes. Por ejemplo, ¿alguna vez ha utilizado una superposición cuadriculada para mapear la posición de un objeto? (Esto se hace a menudo con mapas de carreteras, también).
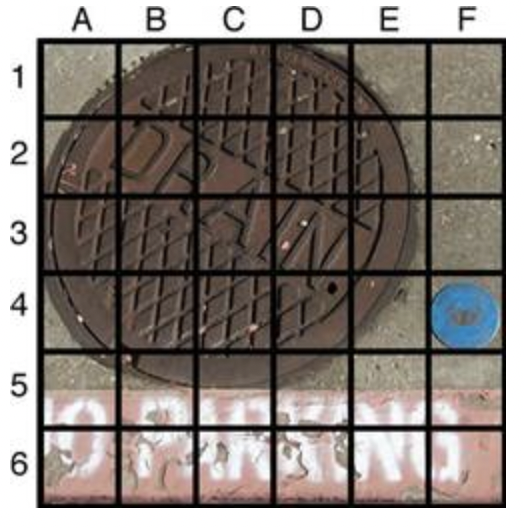
Este “mapa” utiliza una cuadrícula horizontal y vertical para transmitir información sobre la ubicación de un objeto. Observe que las letras A a F están listadas en la parte superior, y los números del 1 al 6 se enumeran a lo largo del borde izquierdo. La ubicación general de cualquier elemento de este mapa se puede encontrar usando la letra y el número de su cuadrícula cuadrada. Por ejemplo, puedes encontrar el ítem que existe en el cuadrado 4 F moviendo tu dedo a lo largo de la horizontal a la letra F y luego recto hacia abajo para que estés en línea con el 4. Encontrarás un disco azul en esta ubicación del mapa.
El plano de coordenadas tiene elementos similares a la rejilla que se muestra arriba. Consiste en un eje horizontal y un eje vertical, líneas numéricos que se cruzan en ángulo recto. (Son perpendiculares entre sí.)
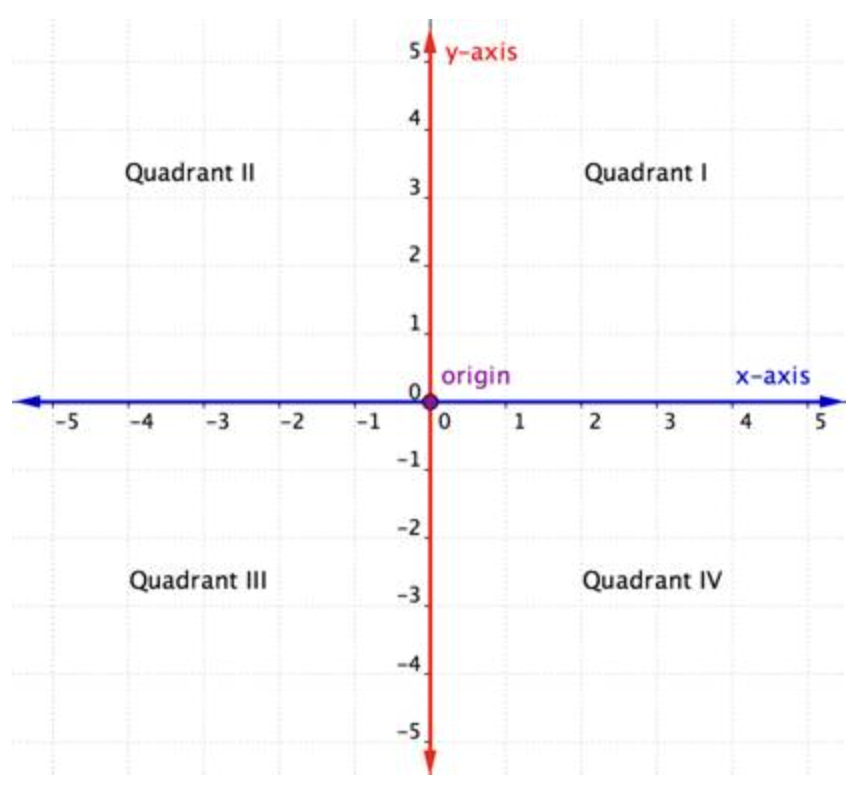
El eje horizontal en el plano de coordenadas se denomina eje x. El eje vertical se llama eje y. El punto en el que se cruzan los dos ejes se denomina origen. El origen está en 0 en el eje x y 0 en el eje y.
Los ejes X e Y que se cruzan dividen el plano de coordenadas en cuatro secciones. Estas cuatro secciones se denominan cuadrantes. Los cuadrantes se nombran usando los números romanos I, II, III y IV comenzando con el cuadrante superior derecho y moviéndose en sentido antihorario.
Las ubicaciones en el plano de coordenadas se describen como pares ordenados. Un par ordenado le indica la ubicación de un punto relacionando la ubicación del punto a lo largo del eje x (el primer valor del par ordenado) y a lo largo del eje y (el segundo valor del par ordenado).
En un par ordenado, como (x, y), el primer valor se llama coordenada x y el segundo valor es la coordenada y. Tenga en cuenta que la coordenada x aparece antes de la coordenada y. Dado que el origen tiene una coordenada x de 0 y una coordenada y de 0, su par ordenado se escribe (0, 0).
Considera el punto a continuación.
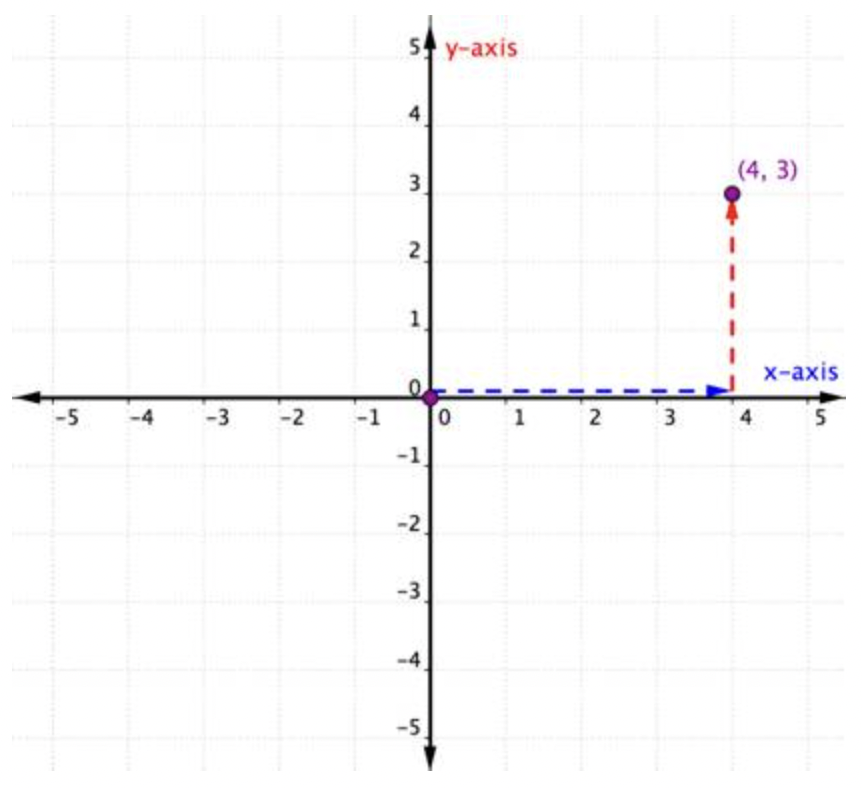
Para identificar la ubicación de este punto, comience en el origen (0, 0) y muévase a la derecha a lo largo del eje x hasta que esté debajo del punto. Mira la etiqueta en el eje x. El 4 indica que, desde el origen, has recorrido cuatro unidades a la derecha a lo largo del eje x. Esta es la coordenada x, el primer número del par ordenado.
Desde 4 en el eje x se mueven hacia arriba hasta el punto y notan el número con el que se alinea en el eje y. El 3 indica que, después de abandonar el eje x, viajó 3 unidades hacia arriba en la dirección vertical, la dirección del eje y. Este número es la coordenada y, el segundo número en el par ordenado. Con una coordenada x de 4 y una coordenada y de 3, se tiene el par ordenado (4, 3).
Veamos otro ejemplo.
Describir el punto mostrado como un par ordenado.
Solución
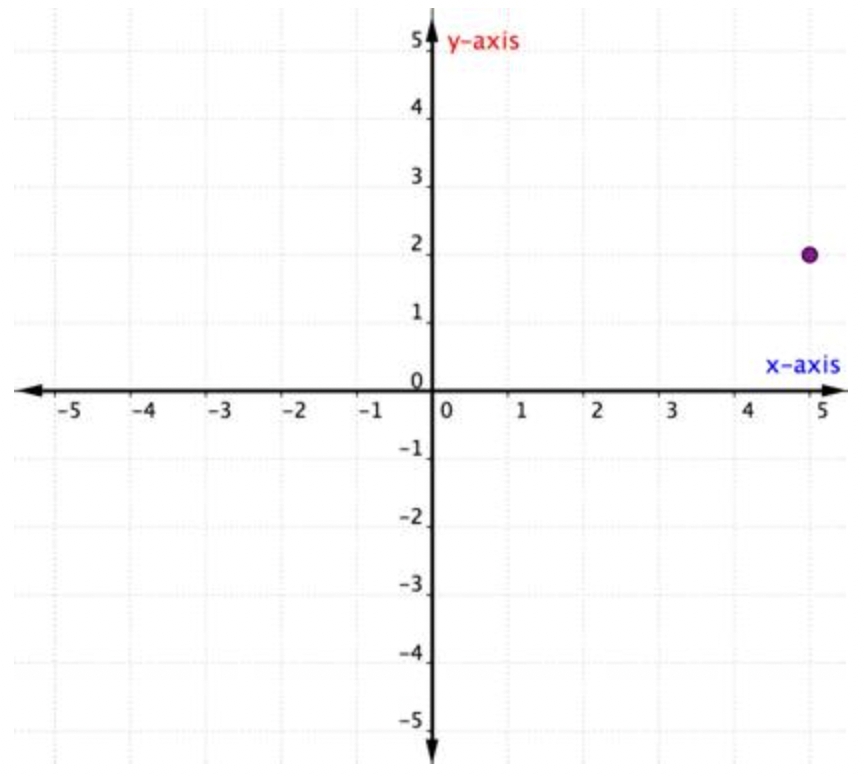
| (5,y) | Comience en el origen y muévase a lo largo del eje x. Esta es la coordenada x y se escribe primero en el par ordenado. |
| (5,2) | Pasar de 5 hasta el par ordenado y leer el número en el eje y. Esta es la coordenada y y se escribe en segundo lugar en el par ordenado. |
El punto que se muestra como un par ordenado es (5, 2).
Trazado de puntos en el plano de coordenadas
Ahora que sabes cómo usar los ejes x e y, también puedes trazar un par ordenado. Solo recuerda, ambos procesos comienzan en el origen, ¡el principio! El ejemplo que sigue muestra cómo graficar el par ordenado (1, 3).
Trazar el punto (1, 3).
Solución
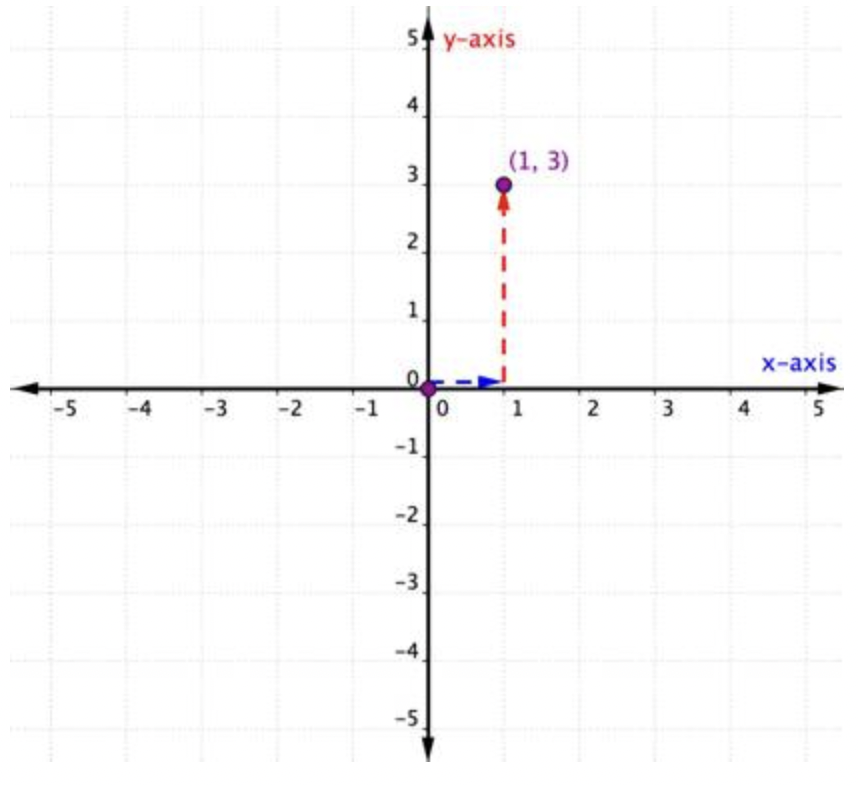
| La coordenada x es 1 porque viene primero en el par ordenado. Comience en el origen y mueva una distancia de 1 unidad en una dirección positiva (hacia la derecha) desde el origen a lo largo del eje x. | La coordenada y es 3 porque viene en segundo lugar en el par ordenado. De aquí se mueven directamente 3 unidades en una dirección positiva (arriba). Si miras hacia el eje y, deberías estar alineado con 3 en ese eje. |
Dibuja un punto en esta ubicación y etiquete el punto (1, 3).
En el ejemplo anterior, tanto las coordenadas x como las y fueron positivas. Cuando una (o ambas) de las coordenadas de un par ordenado es negativa, deberá moverse en dirección negativa a lo largo de uno o ambos ejes. Considera el siguiente ejemplo en el que ambas coordenadas son negativas.
Trazar el punto (−4,−2).
Solución
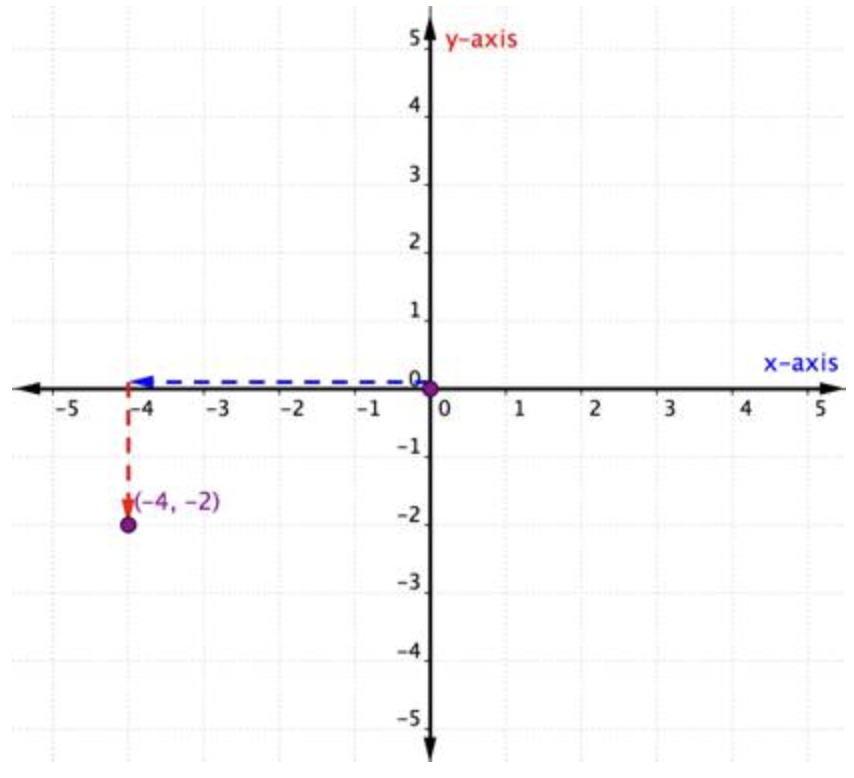
| La coordenada x es -4 porque viene primero en el par ordenado. Comienza en el origen y mueve 4 unidades en dirección negativa (izquierda) a lo largo del eje x. | La coordenada y es -2 porque viene en segundo lugar en el par ordenado. Ahora mueve 2 unidades en dirección negativa (hacia abajo). Si miras hacia el eje y, deberías estar alineado con -2 en ese eje. |
Dibuja un punto en esta ubicación y etiquete el punto (−4,−2).
A continuación se resumen los pasos para trazar un punto.
- Determinar la coordenada x. Comenzando en el origen, muévase horizontalmente, la dirección del eje x, la distancia dada por la coordenada x. Si la coordenada x es positiva, muévase hacia la derecha; si la coordenada x es negativa, muévase hacia la izquierda.
- Determinar la coordenada y. Comenzando en la coordenada x, muévase verticalmente, la dirección del eje y, la distancia dada por la coordenada y. Si la coordenada y es positiva, muévase hacia arriba; si la coordenada y es negativa, baje.
- Dibuja un punto en la ubicación final. Etiquete el punto con el par ordenado.
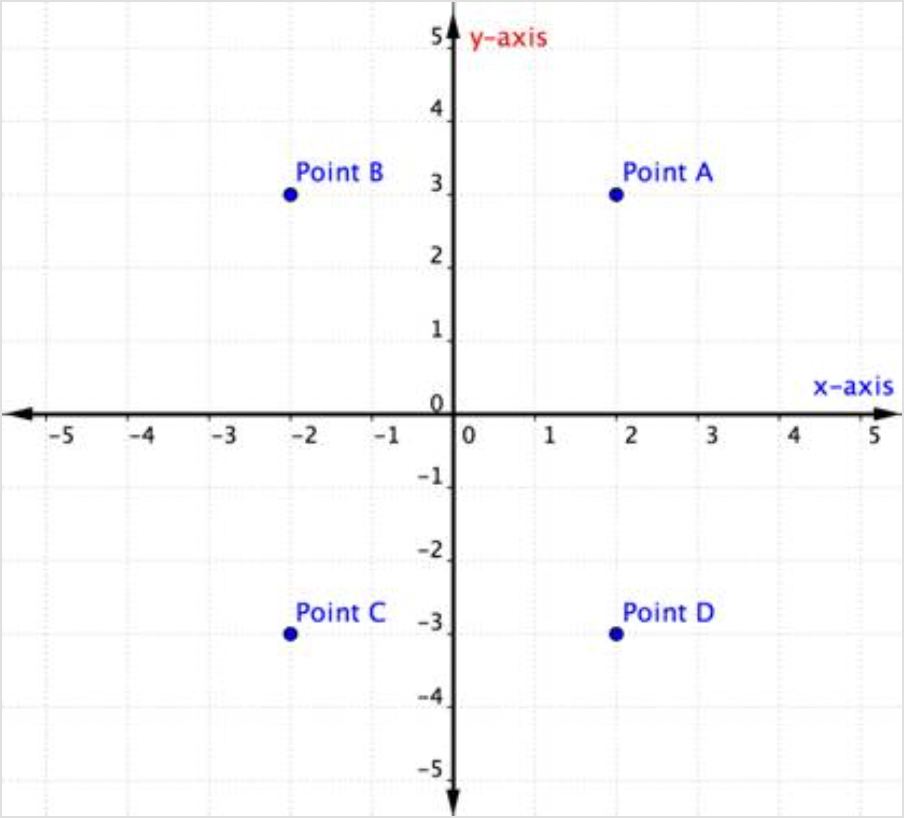
¿Qué punto representa el par ordenado (-2, 3)?
- Contestar
-
El punto B es correcto. Comience en el origen y mueva 2 unidades en la dirección negativa (izquierda) a lo largo del eje x. Luego, mueve 3 unidades en una dirección positiva a lo largo del eje y (3 unidades hacia arriba). Trazar un punto ahí.
Los Cuatro Cuadrantes
Los pares ordenados dentro de cualquier cuadrante en particular comparten ciertas características. Mira cada cuadrante en la gráfica de abajo. ¿Qué nota acerca de los signos de las coordenadas x e y de los puntos dentro de cada cuadrante?
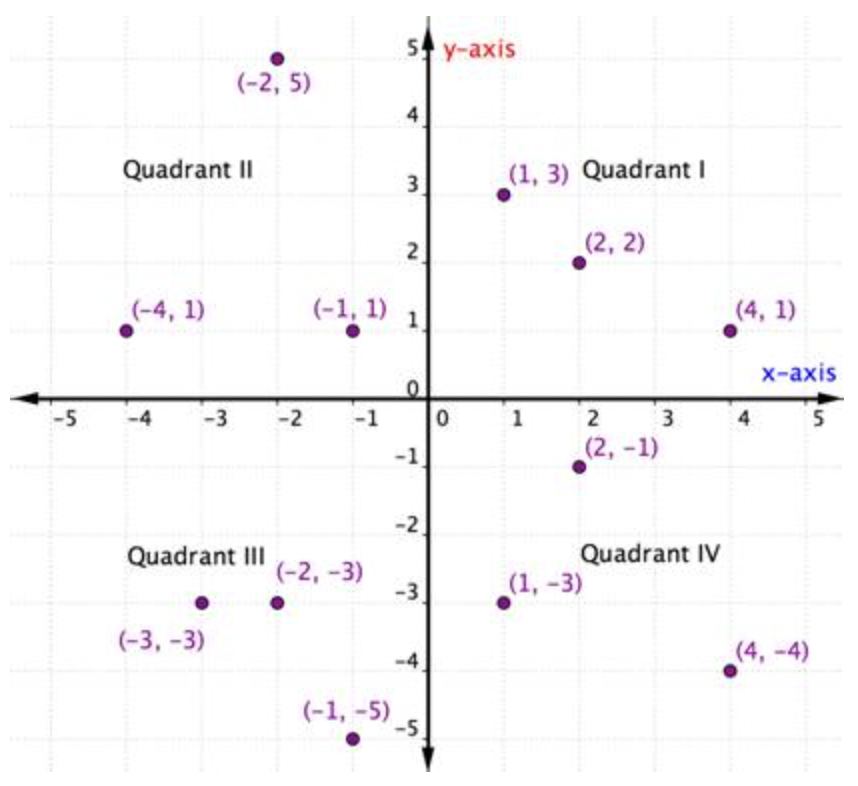
Dentro de cada cuadrante, los signos de las coordenadas x e y de cada par ordenado son los mismos. También siguen un patrón, que se describe en la siguiente tabla.
| Cuadrante | Forma General de Punto en este Cuadrante | Ejemplo | Descripción |
| I | (+,+) | (5,4) | Comenzando desde el origen, vaya a lo largo del eje x en una dirección positiva (derecha) y a lo largo del eje y en una dirección positiva (hacia arriba). |
| II | (−,+) | (−5,4) | Comenzando desde el origen, vaya a lo largo del eje x en una dirección negativa (izquierda) y a lo largo del eje y en una dirección positiva (hacia arriba). |
| III | (−,−) | (−5,−4) | Comenzando desde el origen, vaya a lo largo del eje x en dirección negativa (izquierda) y a lo largo del eje y en dirección negativa (hacia abajo). |
| IV | (+,−) | (5,−4) | Comenzando desde el origen, vaya a lo largo del eje x en una dirección positiva (derecha) y a lo largo del eje y en una dirección negativa (hacia abajo). |
Una vez que conoces los cuadrantes en el plano de coordenadas, puedes determinar el cuadrante de un par ordenado sin siquiera graficarlo mirando el gráfico de arriba. Aquí hay otra forma de pensarlo.
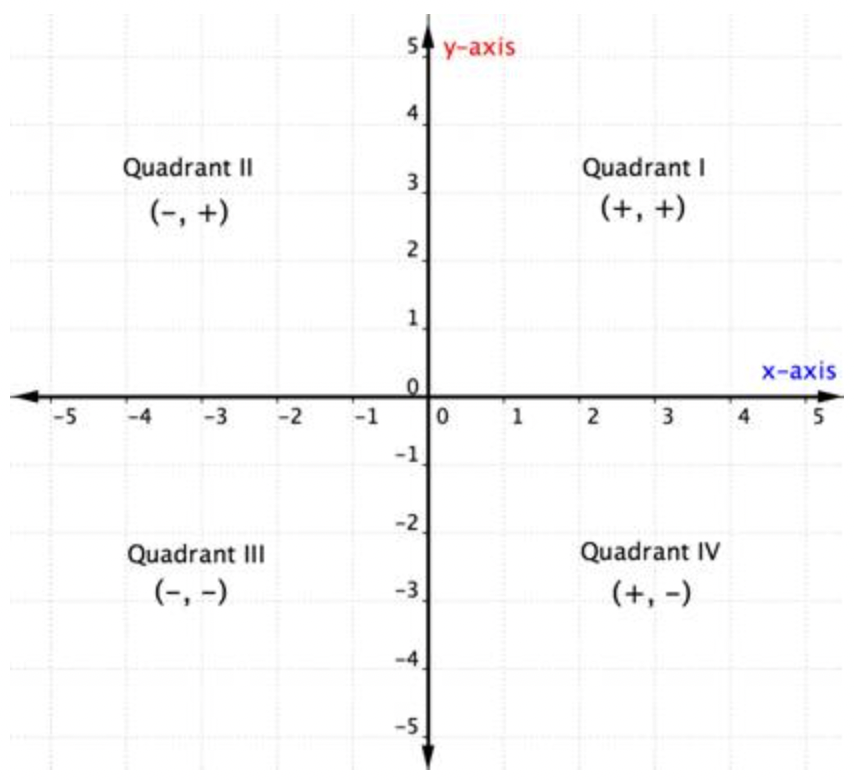
El siguiente ejemplo detalla cómo determinar la ubicación del cuadrante de un punto con solo pensar en los signos de sus coordenadas. Pensar en la ubicación del cuadrante antes de trazar un punto puede ayudarte a prevenir un error. También es un conocimiento útil para comprobar que se ha trazado un punto correctamente.
¿En qué cuadrante se encuentra el punto (-7, 10)?
Solución
| (−7,10) | Mira los signos de las coordenadas x e y. Para este par ordenado, las señales son (−,+). |
| Los puntos con el patrón (−,+) están en el Cuadrante II. | Usando la tabla o cuadrícula de arriba, ubique el patrón (−,+). |
El punto (-7, 10) se encuentra en el Cuadrante II.
¿En qué cuadrante está el punto (-10, -5) lo cated?
Solución
| (−10,−5) | Mira los signos de las coordenadas x e y. Para este par ordenado, las señales son (−,−). |
| Los puntos con el patrón (−,−) están en el Cuadrante III. | Usando la tabla o cuadrícula de arriba, ubique el patrón (−,−). |
El punto (-10, -5) se encuentra en el Cuadrante III.
¿Qué sucede si un par ordenado tiene una coordenada x o y de cero? El siguiente ejemplo muestra la gráfica del par ordenado (0, 4).
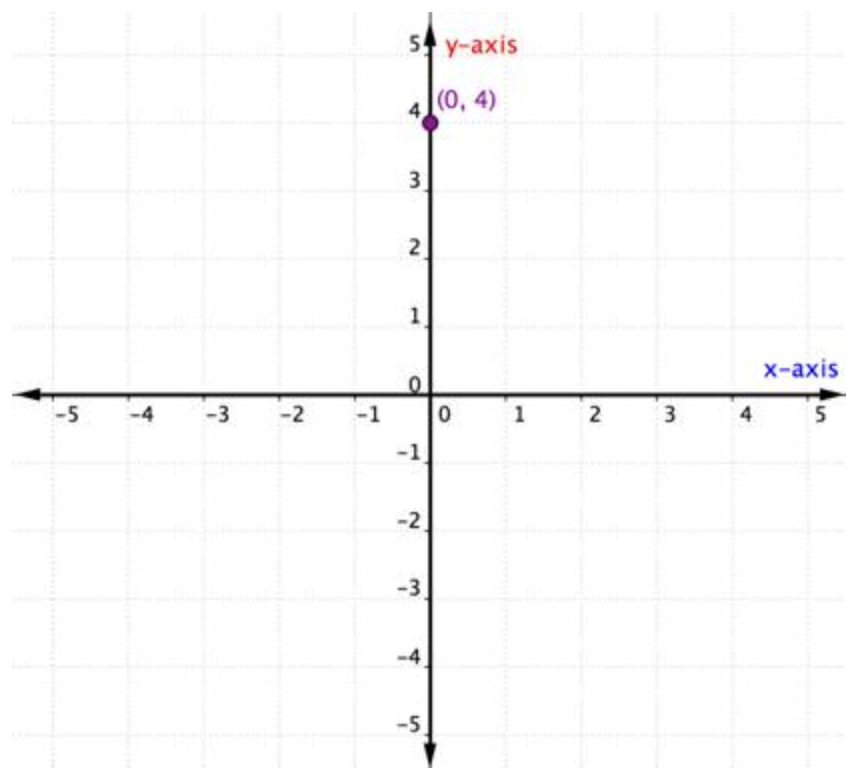
Un punto ubicado en uno de los ejes no se considera que esté en un cuadrante. Es simplemente en uno de los ejes. Siempre que la coordenada x sea 0, el punto se ubica en el eje y. De igual manera, cualquier punto que tenga una coordenada y de 0 se ubicará en el eje x.
¿Cuál de las siguientes descripciones describe mejor la ubicación del punto (8, 0)?
- Cuadrante I
- Está en el eje x
- Está en el eje y
- El plano de coordenadas
- Contestar
-
- Incorrecto. Los ejes no se consideran parte del cuadrante. Más bien, son los límites que definen al cuadrante. La respuesta correcta es el eje x.
- Correcto. Para trazar este punto, comenzarías en el origen y moverías 8 unidades en la dirección positiva a lo largo del eje x. Dado que la coordenada y es 0, no se mueve fuera de la ubicación en el eje x.
- Incorrecto. Dado que la coordenada y es 0, este punto se ubica en el eje x. Para trazar este punto, comenzarías en el origen y moverías 8 unidades en la dirección positiva a lo largo del eje x. Dado que la coordenada y es 0, no se mueve fuera de la ubicación en el eje x. La respuesta correcta es el eje x.
- Incorrecto. Aunque este punto se encuentre en el plano de coordenadas, puede proporcionar una mejor descripción de su ubicación. La respuesta correcta es el eje x.
Resumen
El plano de coordenadas es un sistema para graficar y describir puntos y líneas. El plano de coordenadas está compuesto por un eje x horizontal y un eje y vertical. La intersección de estas líneas crea el origen, que es el punto (0, 0). El plano de coordenadas se divide en cuatro cuadrantes. En conjunto, estas características del sistema de coordenadas permiten la representación gráfica y comunicación sobre puntos, líneas y otros conceptos algebraicos.


