14.1.1: Graficando Sistemas de Ecuaciones Lineales

Última actualización
Guardar como PDF

Page ID: 111523

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Resolver un sistema de ecuaciones lineales mediante la gráfica.
Determinar si un sistema de ecuaciones lineales es consistente o inconsistente.
Determinar si un sistema de ecuaciones lineales es dependiente o independiente.
Determinar si un par ordenado es una solución de un sistema de ecuaciones.
Resolver problemas de aplicación graficando un sistema de ecuaciones.

Introducción

Recordemos que una ecuación lineal grafica como una línea, lo que indica que todos los puntos de la línea son soluciones a esa ecuación lineal. Hay un número infinito de soluciones. Si se tiene un sistema de ecuaciones lineales, la solución para el sistema es el valor que hace que todas las ecuaciones sean verdaderas. Para dos variables y dos ecuaciones, este es el punto donde se cruzan las dos gráficas. Las coordenadas de este punto serán la solución para las dos variables en las dos ecuaciones.

Sistemas de Ecuaciones

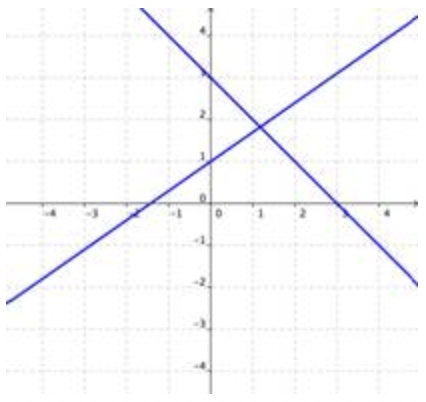
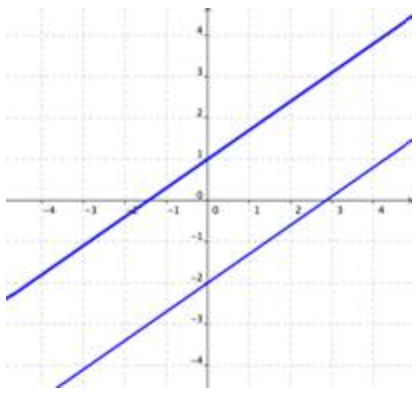
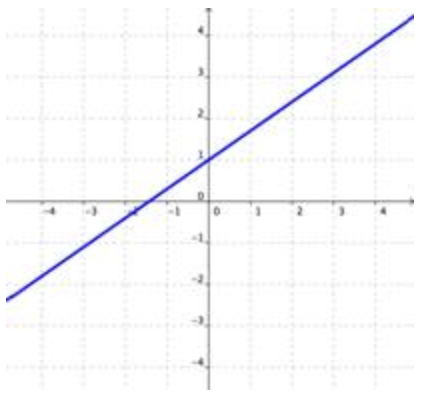
La solución para un sistema de ecuaciones es el valor o valores que son verdaderos para todas las ecuaciones del sistema. Las gráficas de ecuaciones dentro de un sistema pueden indicarle cuántas soluciones existen para ese sistema. Mira las imágenes a continuación. Cada una muestra dos líneas que conforman un sistema de ecuaciones.

Una solución

$Screen Shot 2021-06-28 a las 9.07.42 PM.png$

Si las gráficas de las ecuaciones se cruzan, entonces hay una solución que es verdadera para ambas ecuaciones.

Sin soluciones

$Screen Shot 2021-06-28 a las 9.08.20 PM.png$

Si las gráficas de las ecuaciones no se cruzan (por ejemplo, si son paralelas), entonces no hay soluciones que sean verdaderas para ambas ecuaciones.

Soluciones Infinitas

$Screen Shot 2021-06-28 a las 9.08.47 PM.png$

Si las gráficas de las ecuaciones son las mismas, entonces hay un número infinito de soluciones que son verdaderas para ambas ecuaciones.

Cuando las líneas se cruzan, el punto de intersección es el único punto que las dos gráficas tienen en común, por lo que las coordenadas de ese punto son la solución para las dos variables utilizadas en las ecuaciones. Cuando las líneas son paralelas, no hay soluciones. En ocasiones las dos ecuaciones se graficarán como la misma línea, en cuyo caso tenemos un número infinito de soluciones.

A veces se utilizan términos especiales para describir este tipo de sistemas.

Los siguientes términos se refieren a cuántas soluciones tiene el sistema.

Cuando un sistema tiene una solución (las gráficas de las ecuaciones se cruzan una vez), el sistema es un sistema consistente de ecuaciones lineales y las ecuaciones son independientes.

Cuando un sistema no tiene solución (las gráficas de las ecuaciones no se cruzan en absoluto), el sistema es un sistema inconsistente de ecuaciones lineales y las ecuaciones son independientes.

Si las líneas son las mismas (las gráficas se cruzan en todos los puntos), el sistema es un sistema consistente de ecuaciones lineales y las ecuaciones son dependientes. Es decir, cualquier solución de una ecuación también debe ser una solución de la otra, por lo que las ecuaciones dependen unas de otras.

Los siguientes términos se refieren a si el sistema tiene alguna solución.

El sistema es un sistema consistente de ecuaciones lineales cuando tiene soluciones.

El sistema es un sistema inconsistente de ecuaciones lineales cuando no tiene soluciones.

Podemos resumir esto de la siguiente manera:

Un sistema con una o más soluciones es consistente.
Un sistema sin soluciones es inconsistente.
Si las líneas son diferentes, las ecuaciones son ecuaciones lineales independientes.
Si las líneas son las mismas, las ecuaciones son ecuaciones lineales dependientes.

Ejemplo

Utilizando la gráfica de$\ y=x$ y$\ x+2 y=6$, que se muestra a continuación, determinar cuántas soluciones tiene el sistema. Después se clasifica el sistema como consistente o inconsistente y las ecuaciones como dependientes o independientes.

Solución

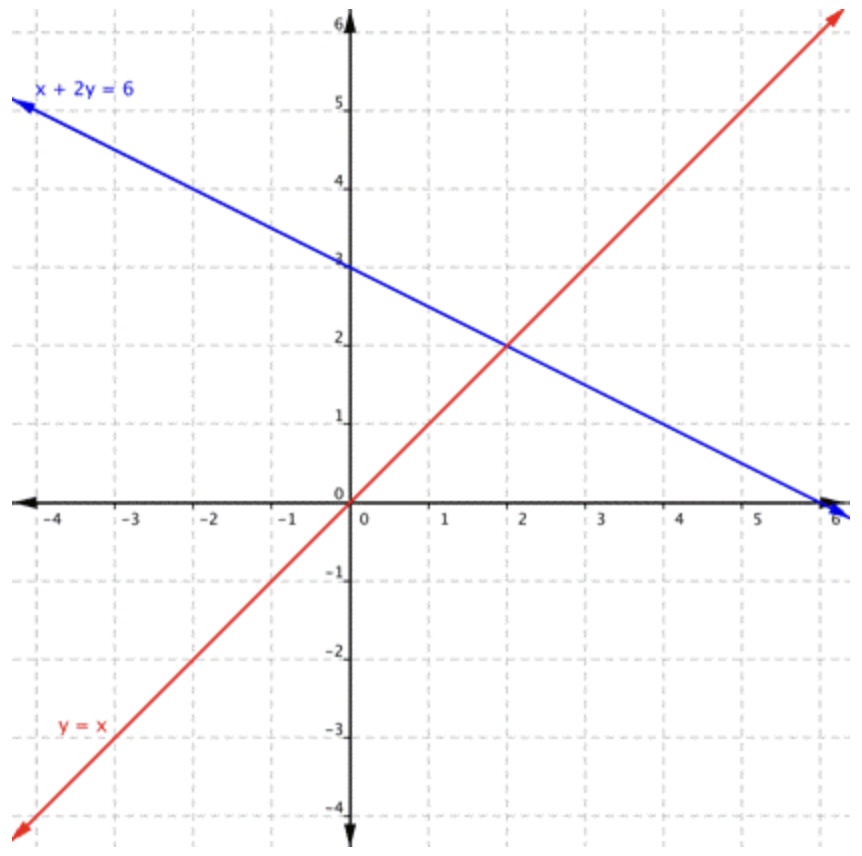$Screen Shot 2021-06-28 a las 9.55.46 PM.png$

Las líneas se cruzan en un punto, por lo que las dos líneas tienen solo un punto en común. Sólo hay una solución para el sistema.

Debido a que las líneas no son las mismas, las ecuaciones son independientes.

Debido a que sólo hay una solución, este sistema es consistente.

El sistema es consistente y las ecuaciones son independientes.

Ejemplo Avanzado

Utilizando la gráfica de$\ y=3.5 x+0.25$ y$\ 14 x-4 y=-4.5$, que se muestra a continuación, determinar cuántas soluciones tiene el sistema. Después se clasifica el sistema como consistente o inconsistente y las ecuaciones como dependientes o independientes.

Solución

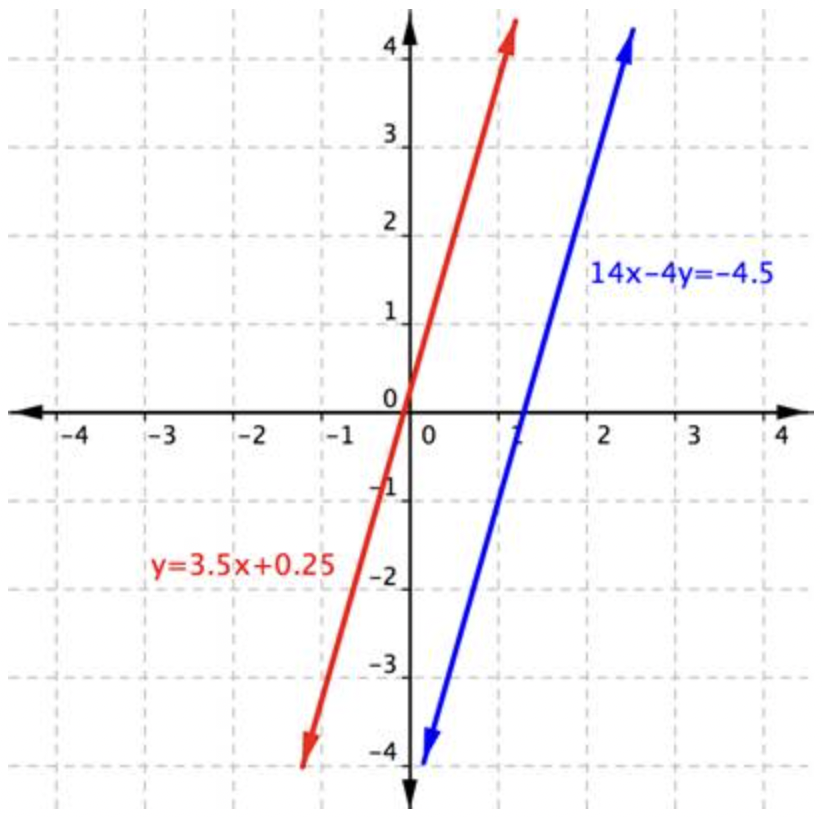$Screen Shot 2021-06-28 a las 9.59.25 PM.png$

Las líneas son paralelas, es decir, no se cruzan. No hay soluciones al sistema.

Debido a que las líneas no son las mismas, las ecuaciones son independientes.

No hay soluciones. Por lo tanto, este sistema es inconsistente.

El sistema es inconsistente y las ecuaciones son independientes.

Pregunta Avanzada

¿Cuál de las siguientes representa ecuaciones dependientes y sistemas consistentes?

\ (\\ begin {array} {l}
y=\ frac {1} {2} x+5\\
-\ frac {1} {2} x+y=-2
\ end {array}\)
\ (\\ begin {array} {l}
y=\ frac {1} {5} x+5\\
\ frac {1} {5} x+y=-\ frac {3} {2}
\ end {array}\)
\ (\\ begin {array} {l}
y=-3 x-1\\
3 x+y=-1
\ end {array}\)
\ (\\ begin {array} {l}
y=3 x-1\\
8 x+y=-1
\ end {array}\)

Contestar

\ (\\ begin {array} {l}
y=\ frac {1} {2} x+5\\
-\ frac {1} {2} x+y=-2
\ end {array}\)

Incorrecto. Las dos líneas en este sistema tienen la misma pendiente, pero diferentes valores para$\ b$. Esto significa que las líneas son paralelas. Las líneas no se cruzan, por lo que no hay soluciones y el sistema es inconsistente. Debido a que las líneas no son las mismas, las ecuaciones son independientes. La respuesta correcta es C.
\ (\\ begin {array} {l}
y=\ frac {1} {5} x+5\\
\ frac {1} {5} x+y=-\ frac {3} {2}
\ end {array}\)

Incorrecto. Las dos líneas en este sistema tienen diferentes pendientes y diferentes valores para$\ b$. Esto significa que las líneas se cruzan en un punto. Dado que hay una solución, este sistema es consistente. Y debido a que las líneas no son las mismas, las ecuaciones son independientes. La respuesta correcta es C.
\ (\\ begin {array} {l}
y=-3 x-1\\
3 x+y=-1
\ end {array}\)

Correcto. Las dos líneas en este sistema son las mismas; se$\ 3 x+y=-1$ pueden reescribir como$\ y=-3 x-1$. Dado que hay muchas soluciones, este sistema es consistente. Las líneas son idénticas por lo que las ecuaciones son dependientes.
\ (\\ begin {array} {l}
y=3 x-1\\
8 x+y=-1
\ end {array}\)

Incorrecto. Las dos líneas en este sistema tienen diferentes pendientes y el mismo valor para$\ b$. Esto significa que las líneas se cruzan en un punto: la intersección y. Recordemos que las líneas que se cruzan tienen una solución y por lo tanto el sistema es consistente. Debido a que las líneas no son las mismas, las ecuaciones son independientes. La respuesta correcta es C.

Verificación de una solución

De la gráfica anterior, se puede ver que hay una solución para el sistema$\ y=x$ y$\ x+2 y=6$. La solución parece ser$\ (2,2)$. No obstante, debes verificar una respuesta que lees de una gráfica para estar seguro de que no es realmente$\ (2.001,2.001)$ o$\ (1.9943,1.9943)$.

Una forma de verificar que el punto existe en ambas líneas es sustituir los valores x e y del par ordenado en la ecuación de cada línea. Si la sustitución da como resultado una declaración verdadera, ¡entonces tienes la solución correcta!

Ejemplo

Es$\ (2,2)$ una solución del sistema$\ y=x$ y$\ x+2 y=6$?

Solución

\ (\\ begin {array} {l}
y=x\
2=2
\ end {array}\)

TRUE

$\ (2,2)$es una solución de$\ y=x$.

\ (\\ begin {array} {l}
x+2 y=6\\
2+2 (2) =6\\
2+4=6\\
6=6
\ end {array}\)

TRUE

$\ (2,2)$es una solución de$\ x+2 y=6$

Dado que la solución del sistema debe ser una solución a todas las ecuaciones del sistema, verifique el punto en cada ecuación. Sustituye 2 por$\ x$ y 2 para$\ y$ en cada ecuación.

$\ (2,2)$es una solución al sistema.

Ya que$\ (2,2)$ es una solución a cada una de las ecuaciones en el sistema,$\ (2,2)$ es una solución al sistema.

Ejemplo

Es$\ (3,9)$ una solución del sistema$\ y=3 x$ y$\ 2 x-y=6$?

Solución

\ (\\ begin {array} {l}
y=3 x\\
9=3 (3)
\ end {array}\)

TRUE

$\ (3,9)$es una solución de$\ y=3 x$.

\ (\\ begin {array} {l}
2 x-y=6\\
2 (3) -9=6\\
6-9=6\\
-3=6
\ end {array}\)

FALSE

$\ (3,9)$no es una solución de$\ 2 x-y=6$.

Dado que la solución del sistema debe ser una solución a todas las ecuaciones del sistema, verifique el punto en cada ecuación. Sustituye 3 por$\ x$ y 9 para$\ y$ en cada ecuación.

$\ (3,9)$no es una solución al sistema.

Ya que no$\ (3,9)$ es una solución de una de las ecuaciones en el sistema, no puede ser una solución al sistema.

Ejemplo

Es$\ (-2,4)$ una solución del sistema$\ y=2 x$ y$\ 3 x+2 y=1$?

Solución

\ (\\ begin {array} {l}
y=2 x\\
4=2 (-2)\\
4=-4
\ end {array}\)

FALSE

$\ (-2,4)$no es una solución de$\ y=2 x$.

\ (\\ begin {array} {l}
3 x+2 y=1\\
3 (-2) +2 (4) =1\\
-6+8=1\\
2=1
\ end {array}\)

FALSE

$\ (-2,4)$no es una solución de$\ 3 x+2 y=1$.

Dado que la solución del sistema debe ser una solución a todas las ecuaciones del sistema, verifique el punto en cada ecuación. Sustituye -2 por$\ x$ y 4 para$\ y$ en cada ecuación.

$\ (-2,4)$no es una solución al sistema.

Ya que no$\ (-2,4)$ es una solución a ninguna de las ecuaciones en el sistema, no$\ (-2,4)$ es una solución del sistema.

Recuerde que, para ser una solución al sistema de ecuaciones, el valor del punto debe ser una solución para ambas ecuaciones. Una vez que encuentras una ecuación para la que el punto es falso, has determinado que no es una solución al sistema.

Ejercicio

¿Cuál de las siguientes afirmaciones es cierta para el sistema$\ 2 x-y=-3$ y$\ y=4 x-1$?

$\ (2,7)$es una solución de una ecuación pero no de la otra, por lo que es una solución del sistema
$\ (2,7)$es una solución de una ecuación pero no de la otra, por lo que no es una solución del sistema
(\ (2,7)\) es una solución de ambas ecuaciones, por lo que es una solución del sistema
(\ (2,7)\) no es una solución de ninguna de las dos ecuaciones, por lo que no es una solución al sistema

Responder

Incorrecto. Si el punto es una solución de una ecuación pero no de la otra, entonces no es una solución del sistema. De hecho, el punto$\ (2,7)$ es una solución de ambas ecuaciones, por lo que es una solución del sistema. Las dos líneas no son idénticas, por lo que es la única solución.
Incorrecto. El punto$\ (2,7)$ es una solución de ambas ecuaciones, por lo que es una solución del sistema. Las dos líneas no son idénticas, por lo que es la única solución.
Correcto. Sustituir 2 por$\ x$ y 7 por$\ y$ da declaraciones verdaderas en ambas ecuaciones, por lo que el punto es una solución a ambas ecuaciones. Eso quiere decir que es una solución al sistema. Las dos líneas no son idénticas, por lo que es la única solución.
Incorrecto. Sustituir 2 por$\ x$ y 7 por$\ y$ da declaraciones verdaderas en ambas ecuaciones, por lo que el punto se encuentra en ambas líneas. Esto quiere decir que es una solución a ambas ecuaciones. También es la única solución para el sistema.

Graficar como método de solución

Se puede resolver un sistema gráficamente. Sin embargo, es importante recordar que debe verificar la solución, ya que la gráfica podría no ser precisa.

Ejemplo

Encuentre todas las soluciones al sistema$\ y-x=1$ y$\ y+x=3$.

Solución

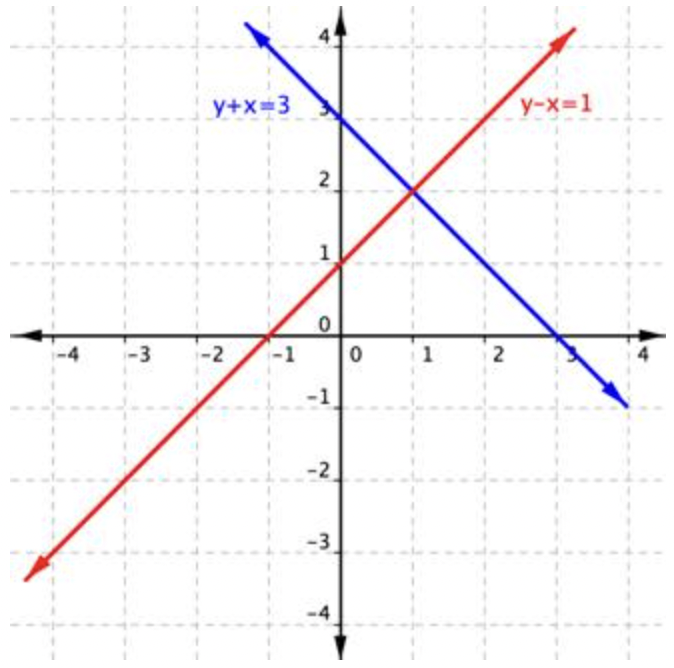$Screen Shot 2021-06-28 a las 10.53.44 PM.png$

Primero, grafica ambas ecuaciones en los mismos ejes.

Las dos líneas se cruzan una vez. Eso significa que solo hay una solución para el sistema.

El punto de intersección parece ser$\ (1,2)$.

Lee el punto de la gráfica con la mayor precisión posible.

\ (\\ begin {array} {r} y-x=1\\ 2-1=1\\ 1=1 \ end {array}\)	\ (\\ begin {array} {r} y+x=3\\ 2+1=3\\ 3=3 \ end {array}\)
TRUE	TRUE
$\ (1,2)$es una solución de$\ y-x=1$.	$\ (1,2)$es una solución de$\ y+x=3$.

Verifique los valores en ambas ecuaciones. Sustituir 1 por$\ x$ y 2 para$\ y$. $\ (1,2)$es una solución.

$\ (1,2)$es la solución al sistema$\ y-x=1$ y$\ y+x=3 y+x=3$.

Ya que$\ (1,2)$ es una solución para cada una de las ecuaciones en el sistema, es la solución para el sistema.

Ejemplo

¿Cuántas soluciones tiene$\ y=2 x+1$ y$\ -4 x+2 y=2$ tiene el sistema?

Solución

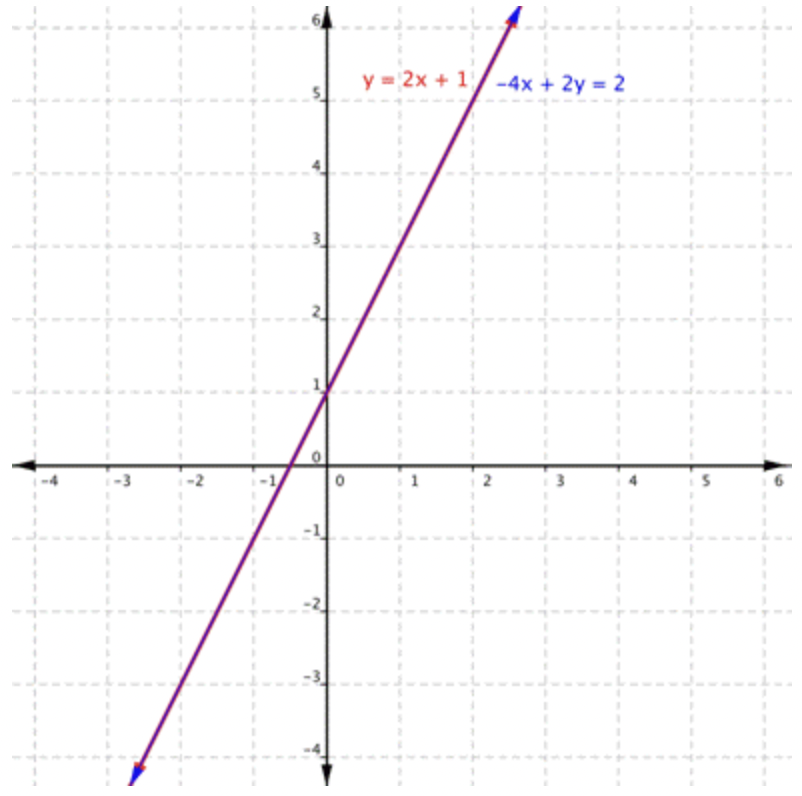$Screen Shot 2021-06-28 at 11.02.48 PM.png$

Primero, grafica ambas ecuaciones en los mismos ejes.

Las dos ecuaciones se graficaron como una misma línea. Entonces cada punto en esa línea es una solución para el sistema de ecuaciones.

El sistema$\ y=2 x+1$ y$\ -4 x+2 y=2$ tiene un número infinito de soluciones.

Ejercicio

¿Qué punto es la solución al sistema$\ x-y=-1$ y$\ 2 x-y=-4$? El sistema se grafica correctamente a continuación.

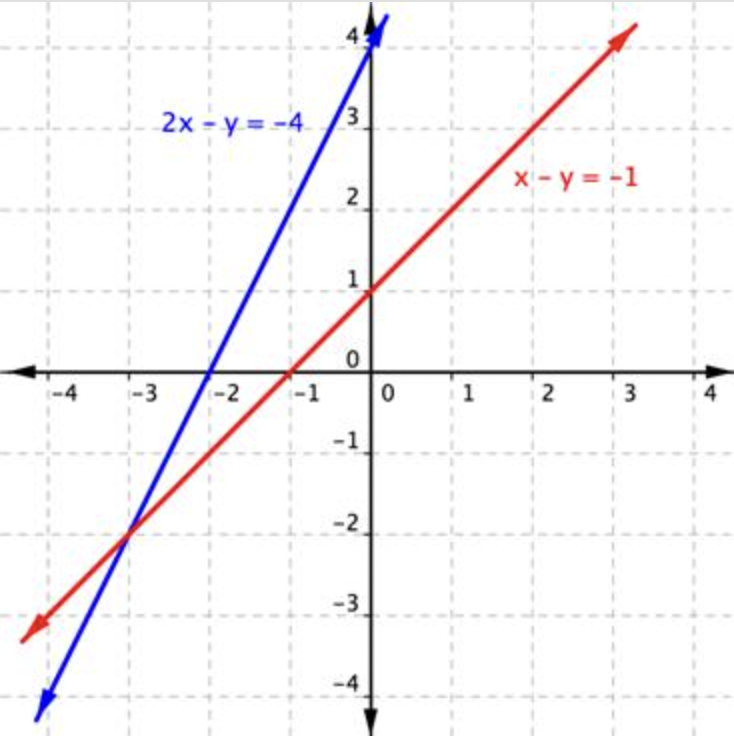
$Screen Shot 2021-06-28 at 11.06.28 PM.png$

$\ (-1,2)$
$\ (-4,-3)$
$\ (-3,-2)$
$\ (-1,1)$

Responder

Incorrecto. Sustituyendo$\ (-1,2)$ en cada ecuación, encuentras que es una solución para$\ 2 x-y=-4$, pero no para$\ x-y=-1$. Esto significa que no puede ser una solución para el sistema. La respuesta correcta es$\ (-3,-2)$.
Incorrecto. Sustituyendo$\ (-4,-3)$ en cada ecuación, encuentras que es una solución para$\ x-y=-1$, pero no para$\ 2 x-y=-4$. Esto significa que no puede ser una solución para el sistema. La respuesta correcta es$\ (-3,-2)$.
Correcto. Sustituir$\ (-3,-2)$ en cada ecuación muestra que este punto es una solución para ambas ecuaciones, por lo que es la solución para el sistema.
Incorrecto. Sustituyendo$\ (-1,-1)$ en cada ecuación, encuentras que no es ni una solución para$\ 2 x-y=-4$, ni para$\ x-y=-1$. Esto significa que no puede ser una solución para el sistema. La respuesta correcta es$\ (-3,-2)$.

Graficar para un contexto del mundo real

Graficar un sistema de ecuaciones para un contexto del mundo real puede ser valioso para visualizar el problema. Veamos un par de ejemplos.

Ejemplo

En el juego de basquetbol de ayer, Cheryl anotó 17 puntos con una combinación de canastas de 2 y 3 puntos. El número de tiros de 2 puntos que hizo fue uno mayor que el número de tiros de 3 puntos que hizo. ¿Cuántos de cada tipo de canasta anotó?

Solución

$\ x$= el número de disparos de 2 puntos realizados

$\ y$= el número de tiros de 3 puntos realizados

Asignar variables a las dos incógnitas: el número de cada tipo de disparos.

$\ 2x$= los puntos de canastas de 2 puntos

$\ 3y$= los puntos de canastas de 3 puntos

Calcula cuántos puntos se hacen de cada uno de los dos tipos de disparos.

El número de puntos que anotó Cheryl (17) = los puntos de canastas de 2 puntos + los puntos de canastas de 3 puntos. $\ 17=2 x+3 y$

Escribir una ecuación usando la información dada en el problema.

El número de canastas de 2 puntos$\ (x)=1+$ el número de canastas de 3 puntos$\ (y)$

Escribir una segunda ecuación usando información adicional dada en el problema.

\ (\\ begin {array} {l}
x=1+y\\
17=2 x+3 y\\
x=1+y
\ end {array}\)

Ahora tienes un sistema de dos ecuaciones con dos variables.

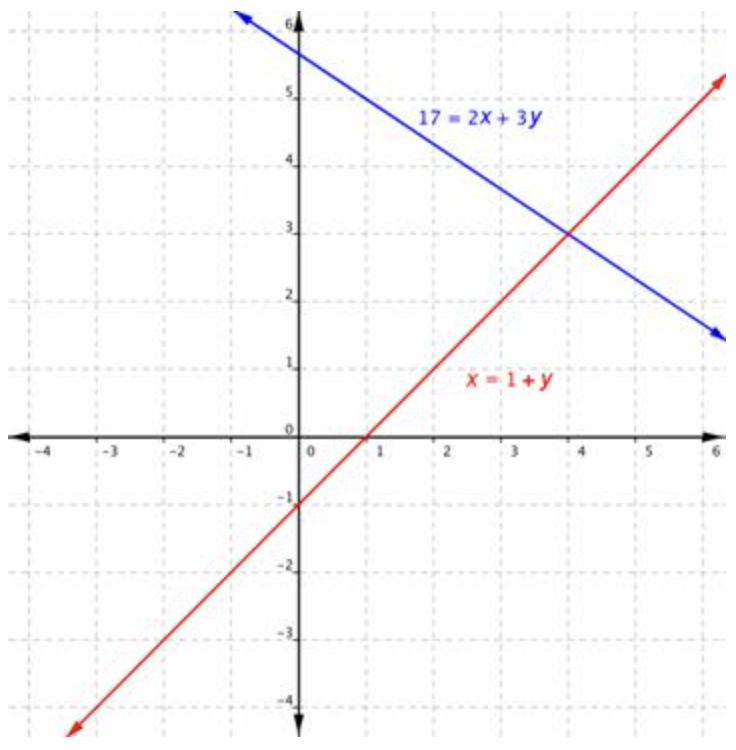$Screen Shot 2021-06-28 a las 11.27.15 PM.png$

Grafica ambas ecuaciones en los mismos ejes.

Las dos líneas se cruzan, por lo que tienen sólo un punto en común. Eso significa que solo hay una solución para el sistema.

El punto de intersección parece ser$\ (4,3)$.

Lee el punto de intersección de la gráfica.

\ (\\ begin {array} {l} 17=2 x+3 y\\ 17=2 (4) +3 (3)\\ 17=8+9\\ 17=17 \ end {array}\)	\ (\\ begin {array} {l} x=1+y\\ 4=1+3\\ 4=4 \ end {array}\)
TRUE	TRUE
$\ (4,3)$es una solución de$\ 17=2 x+3 y$.	$\ (4,3)$es una solución de$\ x=1+y$

Verifica$\ (4,3)$ cada ecuación para ver si es una solución al sistema de ecuaciones.

$\ x=4$y$\ y=3$

Cheryl hizo 4 canastas de dos puntos y 3 canastas de tres puntos.

Ejemplo

Andrés estaba tratando de decidir cuál de los dos planes de telefonía celular debía comprar. Un plan, Talkalot, cobró una tarifa fija de$\ \$ 15$ por mes por minutos ilimitados. Otro plan, FriendFone, cobró una cuota mensual de$\ \$ 5$ además de cobrar 20¢ por minuto por llamadas.

Para examinar la diferencia de planes, hizo una gráfica:

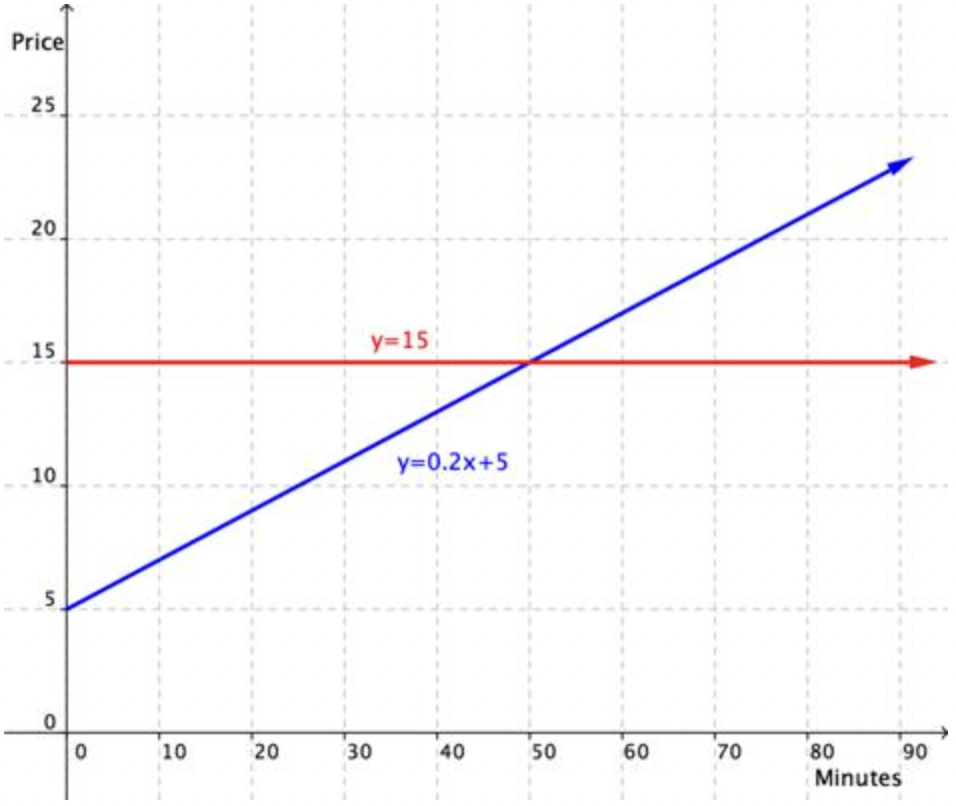
$Screen Shot 2021-06-29 a las 12.00.45 AM.png$

Si planea hablar por teléfono unos 70 minutos al mes, ¿qué plan debería comprar?

Solución

Mira la gráfica. TalkaLot se representa como$\ y=15$, mientras que FriendFone se representa como$\ y=0.2 x+5$.

El número de minutos se enumera en el eje x. Cuando$\ x=70$, TalkaLot cuesta 15 dólares, mientras que FriendFone cuesta alrededor de 19 dólares.

Andrés debería comprar el plan Talkalot.

Dado que Talkalot cuesta menos a los 70 minutos, Andrés debería comprar ese plan.

Tenga en cuenta que si la estimación para FriendFone hubiera sido incorrecta, se podría haber hecho una nueva estimación. Regrafiar para acercar el área donde se cruzan las líneas ayudaría a hacer una mejor estimación.

Ejercicio

Paco y Lisel gastaron 30 dólares yendo al cine anoche. Paco gastó $8 más que Lisel.

Si$\ P$ = la cantidad que gastó Paco, y$\ L$ = la cantidad que gastó Lisel, ¿qué sistema de ecuaciones puedes usar para averiguar cuánto gastó cada una de ellas?

\ (\\ begin {array} {l}
P+L=30\\
P+8=L
\ end {array}\)
\ (\\ begin {array} {l}
P+L=30\\
P=L+8
\ end {array}\)
\ (\\ begin {array} {l}
P+30=L\\
P-8=L
\ end {array}\)
\ (\\ comenzar {matriz} {l}
L+30=P\\
L-8=P
\ final {matriz}\)

Responder

\ (\\ begin {array} {l}
P+L=30\\
P+8=L
\ end {array}\)

Incorrecto. $\ P+8=L$dice: “Lisel gastó 8 dólares más que Paco”. El sistema correcto es:\ (\\ begin {array} {l}
P+L=30\\
P=L+8
\ end {array}\)
\ (\\ begin {array} {l}
P+L=30\\
P=L+8
\ end {array}\)

Correcto. La cantidad total gastada$\ (P+L)$ es de 30, por lo que una ecuación debe ser$\ P+L=30$. Paco gastó 8 dólares más que Lisel, así que te$\ L+8$ dará la cantidad que gastó Paco. Esto puede ser reescrito$\ P=L+8$.
\ (\\ begin {array} {l}
P+30=L\\
P-8=L
\ end {array}\)

Incorrecto. $\ P+30=L$dice: “Lisel gastó 30 dólares más que Paco”. El sistema correcto es:\ (\\ begin {array} {l}
P+L=30\\
P=L+8
\ end {array}\)
\ (\\ comenzar {matriz} {l}
L+30=P\\
L-8=P
\ final {matriz}\)

Incorrecto. $\ L+30=P$dice: “Paco gastó 30 dólares más que Lisel”. El sistema correcto es:\ (\\ begin {array} {l}
P+L=30\\
P=L+8
\ end {array}\)

Resumen

Un sistema de ecuaciones lineales es dos o más ecuaciones lineales que tienen las mismas variables. Puede graficar las ecuaciones como un sistema para averiguar si el sistema no tiene soluciones (representadas por líneas paralelas), una solución (representada por líneas que se cruzan) o un número infinito de soluciones (representadas por dos líneas superpuestas). Si bien graficar sistemas de ecuaciones es una técnica útil, confiar en gráficas para identificar un punto de intersección específico no siempre es una manera precisa de encontrar una solución precisa para un sistema de ecuaciones.