14.1.2: Graficando Sistemas de Desigualdades
- Page ID
- 111522
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Resolver un sistema de desigualdades lineales mediante la representación gráfica.
- Determinar si un par ordenado es una solución de un sistema de desigualdades.
- Resolver problemas de aplicación graficando un sistema de desigualdades.
Introducción
Una solución de un sistema de igualdades lineales es cualquier par ordenado que sea cierto para todas las ecuaciones del sistema. De igual manera, una solución de un sistema de desigualdades lineales es cualquier par ordenado que sea una solución para todas las desigualdades en el sistema.
Se utilizan gráficas para mostrar todos los valores que son soluciones para un sistema de desigualdades lineales.
Graficando un Sistema de Dos Desigualdades
La gráfica de una sola desigualdad lineal divide el plano de coordenadas en dos regiones. Por un lado se encuentran todas las soluciones a la desigualdad. Por otro lado, no hay soluciones. Considera la gráfica de la desigualdad\(\ y<2 x+5\).
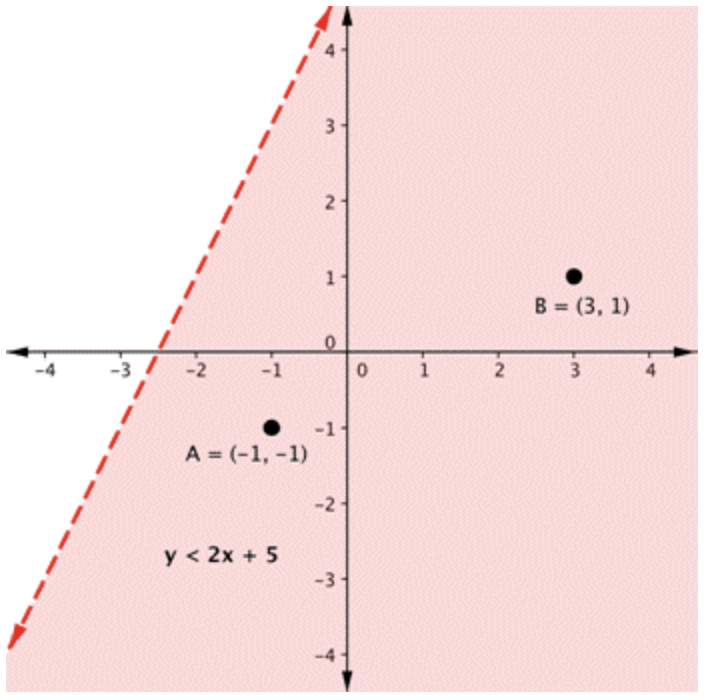
La línea discontinua es\(\ y=2 x+5\). Cada par ordenado en el área coloreada debajo de la línea es una solución para\(\ y<2 x+5\), ya que todos los puntos debajo de la línea harán que la desigualdad sea verdadera. Si lo dudas, intente sustituir las\(\ y\) coordenadas\(\ x\) y de los puntos A y B en la desigualdad, ya verá que funcionan. Entonces, el área sombreada muestra todas las soluciones para esta desigualdad.
La línea límite divide el plano en dos medios planos. En este caso, se muestra como una línea discontinua, ya que los puntos en la línea no satisfacen la desigualdad. Si la desigualdad hubiera sido\(\ y \leq 2 x+5\), entonces la línea limítrofe habría sido sólida.
Vamos a graficar otra desigualdad:\(\ y>-x\) Puedes verificar un par de puntos para determinar a qué lado de la línea límite sombrear. Al verificar los puntos M y N se obtienen declaraciones verdaderas. Entonces, sombreamos el área por encima de la línea. La línea es discontinua, ya que los puntos en la línea no satisfacen la desigualdad.
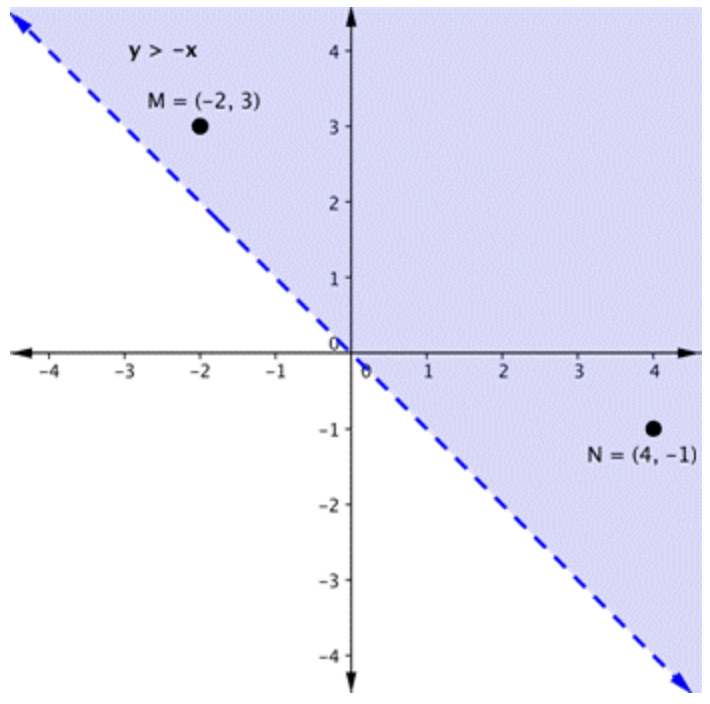
Para crear un sistema de desigualdades, es necesario graficar dos o más desigualdades juntas. Vamos a usar\(\ y<2 x+5\) y\(\ y>-x\) ya que ya hemos graficado cada uno de ellos.
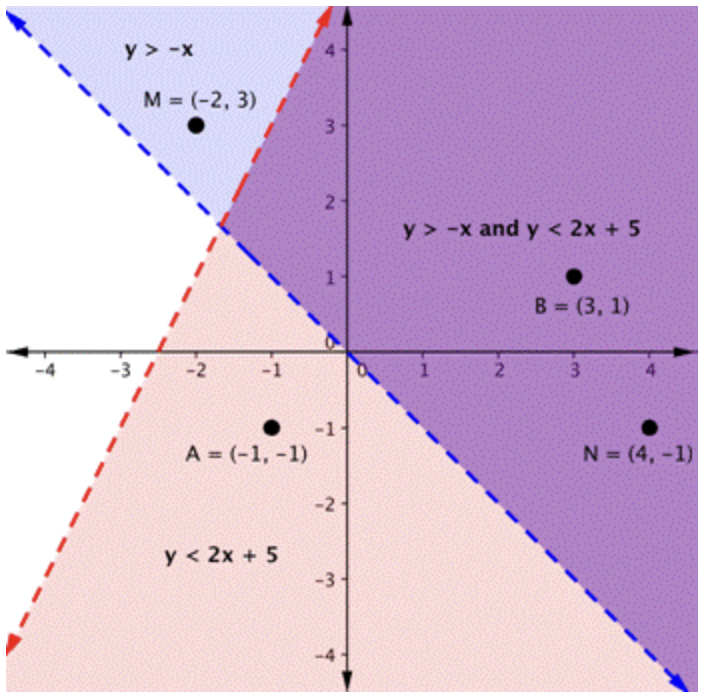
El área púrpura muestra dónde se superponen las soluciones de las dos desigualdades. Esta área es la solución al sistema de desigualdades. Cualquier punto dentro de esta región púrpura será cierto para ambos\(\ y>-x\) y\(\ y<2 x+5\).
En la gráfica, se puede ver que los puntos B y N son soluciones para el sistema porque sus coordenadas harán que ambas desigualdades sean verdaderas declaraciones.
En contraste, los puntos M y A se encuentran fuera de la región de la solución (púrpura). Si bien el punto M es una solución para la desigualdad\(\ y>-x\) y el punto A es una solución para la desigualdad\(\ y<2 x+5\), ninguno de los dos puntos es una solución para el sistema.
¿El punto es\(\ (2,1)\) una solución del sistema\(\ x+y>1\) y\(\ 2 x+y<8\)?
Solución
|
Verifica el punto con cada una de las desigualdades. Sustituir 2 por\(\ x\) y 1 para\(\ y\). ¿El punto es una solución de ambas desigualdades? | ||||||
| El punto\(\ (2,1)\) es una solución del sistema\(\ x+y>1\) y\(\ 2 x+y<8\) | Ya que\(\ (2,1)\) es una solución de cada desigualdad, también es una solución del sistema. |
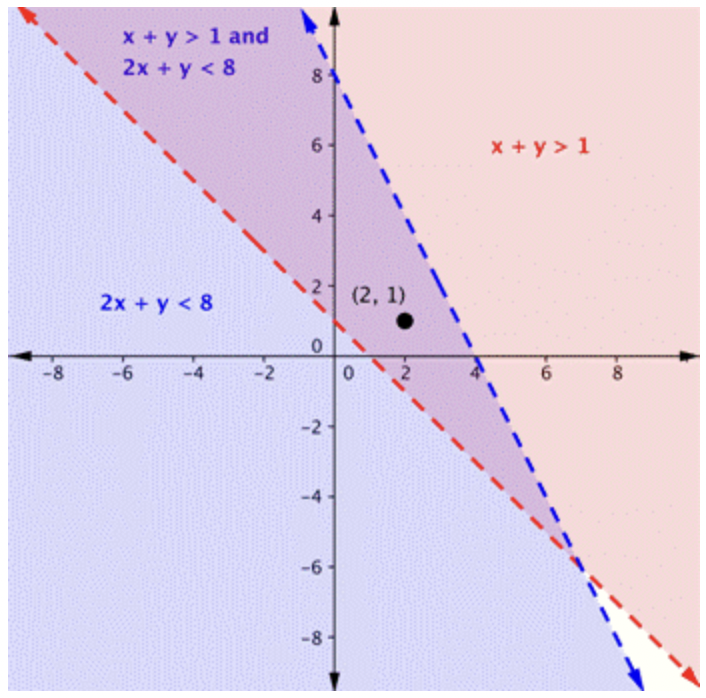
Aquí hay una gráfica del sistema en el ejemplo anterior. Observe que\(\ (2,1)\) se encuentra en el área púrpura, que es el área superpuesta para las dos desigualdades.
¿El punto es\(\ (2,1)\) una solución del sistema\(\ x+y>1\) y\(\ 3 x+y<4\)?
Solución
|
Verifica el punto con cada una de las desigualdades. Sustituir 2 por\(\ x\) y 1 para\(\ y\). ¿El punto es una solución de ambas desigualdades? | ||||||
|
El punto no\(\ (2,1)\) es una solución del sistema. \(\ x+y>1\)y\(\ 3 x+y<4\). |
Ya que no\(\ (2,1)\) es una solución de una de las desigualdades, no es una solución del sistema. |
Aquí hay una gráfica de este sistema. Observe que no\(\ (2,1)\) está en el área púrpura, que es el área superpuesta; es una solución para una desigualdad (la región roja), pero no es una solución para la segunda desigualdad (la región azul).
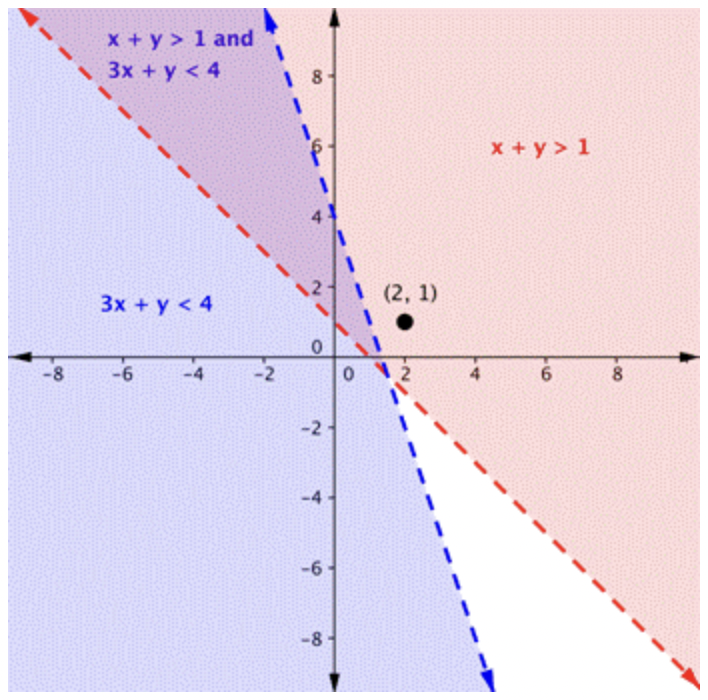
¿Cuáles de los puntos enumerados a continuación son soluciones para el sistema?
\ (\\ begin {array} {l}
y>x\
x-2<0
\ end {array}\)
- \(\ (1,1)\)
- \(\ (-5,9)\)
- \(\ (0,7)\)
- I y II
- II y III
- I y III
- II solamente
- Contestar
-
- Incorrecto. \(\ (-5,9)\)es una solución a este sistema, pero no lo\(\ (1,1)\) es, porque no es una solución a la primera desigualdad. La respuesta correcta es B,\(\ (-5,9)\) y\(\ (0,7)\) son soluciones al sistema.
- Correcto. Los puntos\(\ (-5,9)\) y ambos\(\ (0,7)\) son soluciones para ambas desigualdades en el sistema.
- Incorrecto. \(\ (1,1)\)es una solución válida para la desigualdad\(\ x-2<0\), pero no es una solución para\(\ y>x\); en consecuencia, no es una solución para el sistema. La respuesta correcta es B,\(\ (-5,9)\) y\(\ (0,7)\) son soluciones al sistema.
- Incorrecto. \(\ (-5,9)\)es una solución válida para el sistema, pero también lo es\(\ (0,7)\). La respuesta correcta es B,\(\ (-5,9)\) y\(\ (0,7)\) son soluciones al sistema.
Resolviendo Sistemas de Desigualdades Graficando
Como se mostró anteriormente, encontrar las soluciones de un sistema de desigualdades se puede hacer graficando cada desigualdad e identificando la región que comparten.
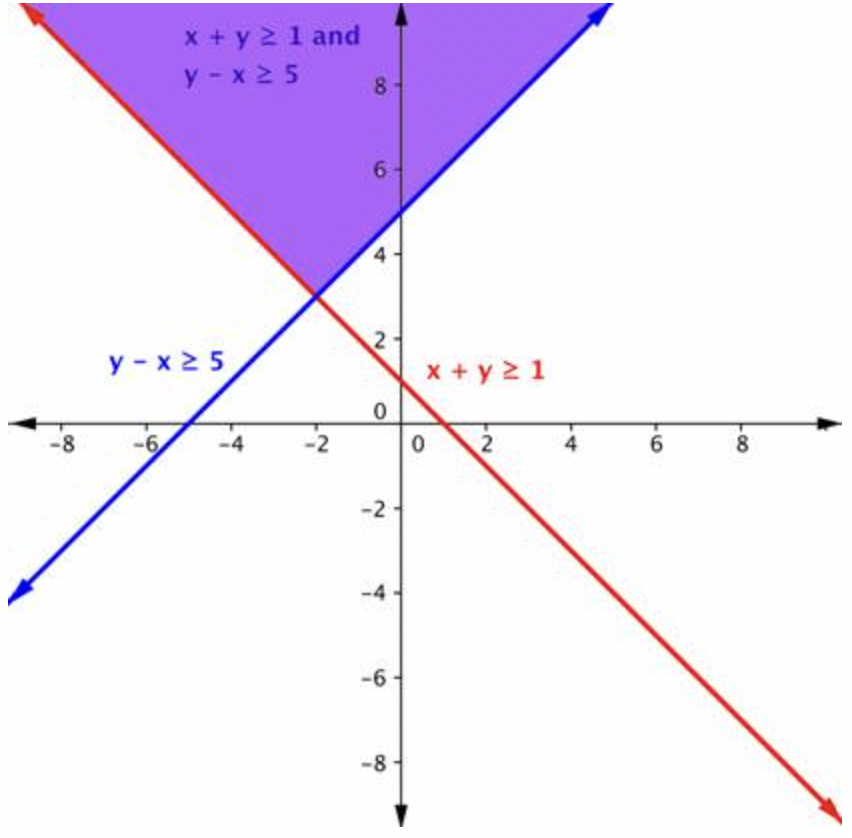
Encuentre la solución al sistema\(\ x+y \geq 1\) y\(\ y-x \geq 5\).
Solución
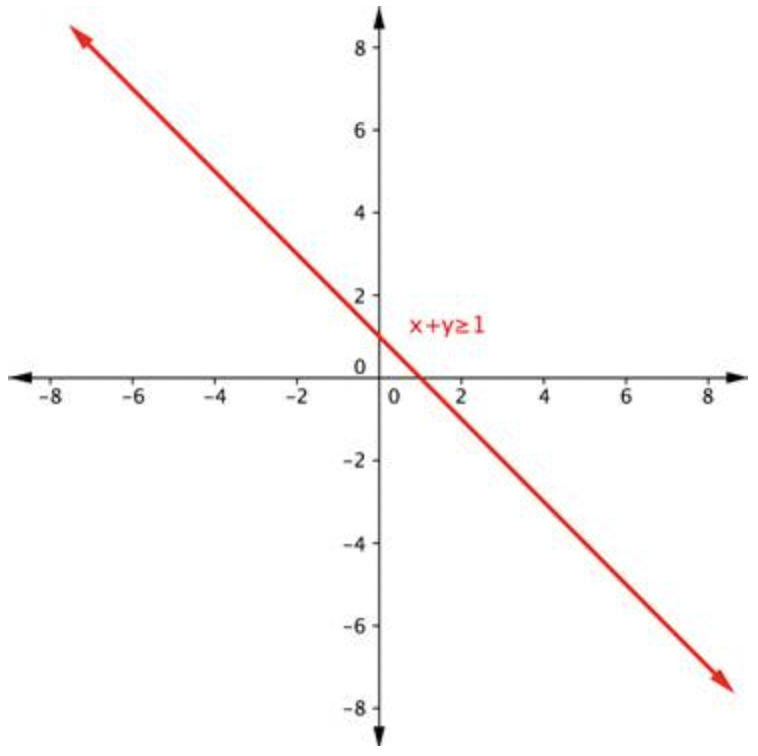 |
Grafica una desigualdad. Primero, grafica la línea límite usando una tabla de valores, intercepciones o cualquier otro método que prefieras. La línea de límite para\(\ x+y \geq 1\) es\(\ x+y=1\), o\(\ y=-x+1\). Dado que el signo igual se incluye con el signo mayor que, la línea límite es sólida. |
||||
|
Encuentra un par ordenado a cada lado de la línea de límite. Inserte los valores x e y en la desigualdad\(\ x+y \geq 1\) y vea qué par ordenado da como resultado una declaración verdadera. | ||||
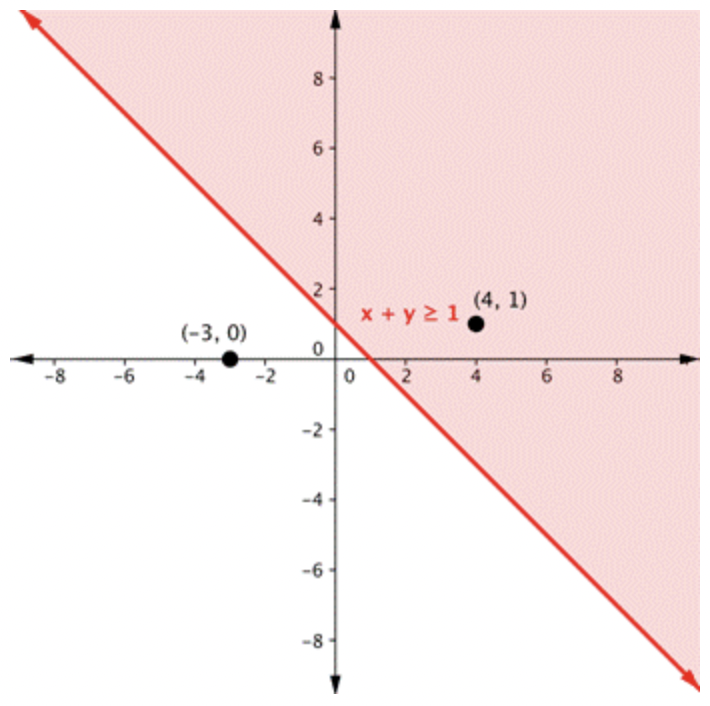 |
Dado que\(\ (4,1)\) resulta en una declaración verdadera, la región que incluye\(\ (4,1)\) debe ser sombreada. | ||||
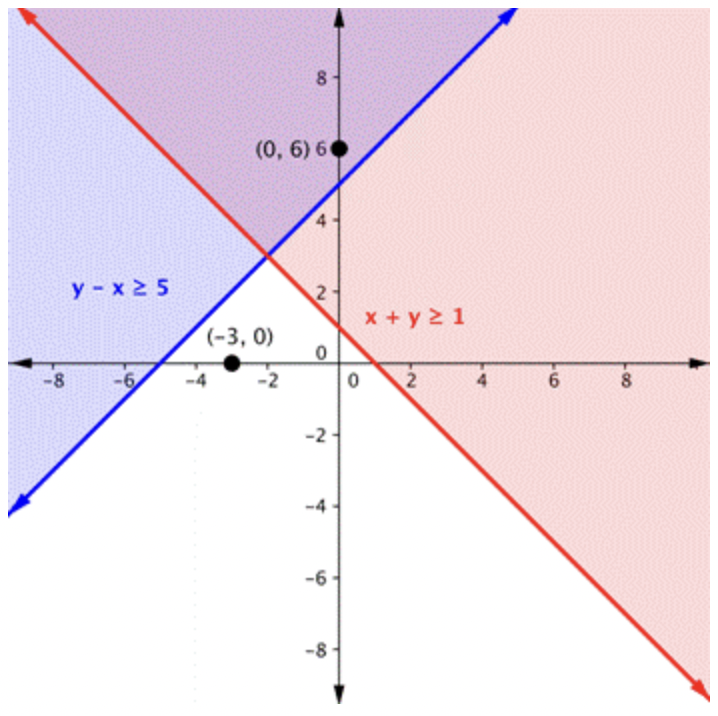 |
Haz lo mismo con la segunda desigualdad. Grafique la línea límite, luego pruebe los puntos para encontrar qué región es la solución a la desigualdad. En este caso, la línea límite es\(\ y-x=5\) (o\(\ y=x+5\)) y es sólida. \(\ (-3,0)\)El punto de prueba no es una solución de\(\ y-x \geq 5\), y el punto de prueba\(\ (0,6)\) es una solución. |
La región púrpura en esta gráfica muestra el conjunto de todas las soluciones del sistema.
Encuentre la solución al sistema\(\ 3 x+2 y<12\) y\(\ -1 \leq y \leq 5\).
Solución
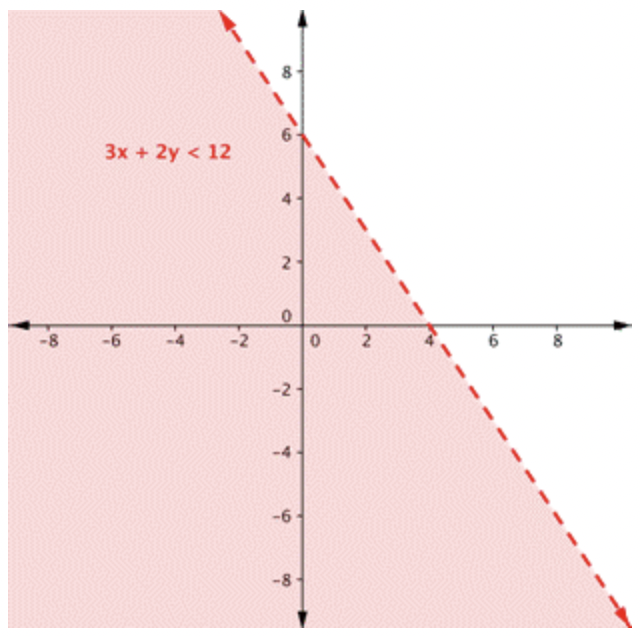 |
Grafica una desigualdad. Primero, grafica la línea límite, luego prueba los puntos. Recuerde, debido a que la desigualdad\(\ 3 x+2 y<12\) no incluye el signo igual, dibuje una línea fronteriza discontinua. Al probar un punto como\(\ (0,0)\) se mostrará que el área por debajo de la línea es la solución a esta desigualdad. |
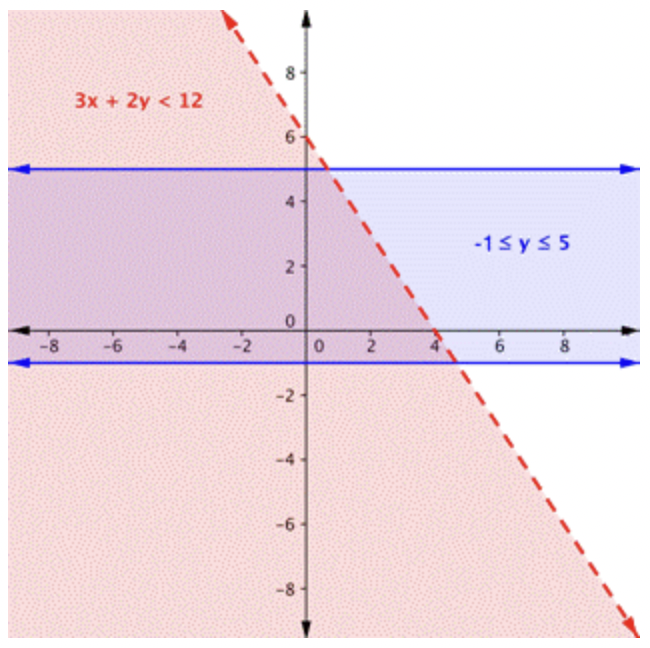 |
La desigualdad\(\ -1 \leq y \leq 5\) es en realidad dos desigualdades:\(\ -1 \leq y\), y\(\ y \leq 5\). Otra forma de pensar en esto es que\(\ y\) debe estar entre -1 y 5. Las líneas de borde para ambos son horizontales. La región entre esas dos líneas contiene las soluciones de\(\ -1 \leq y \leq 5\). Hacemos las líneas sólidas porque también queremos incluir\(\ y=-1\) y\(\ y=5\). Grafica esta región en los mismos ejes que la otra desigualdad. |
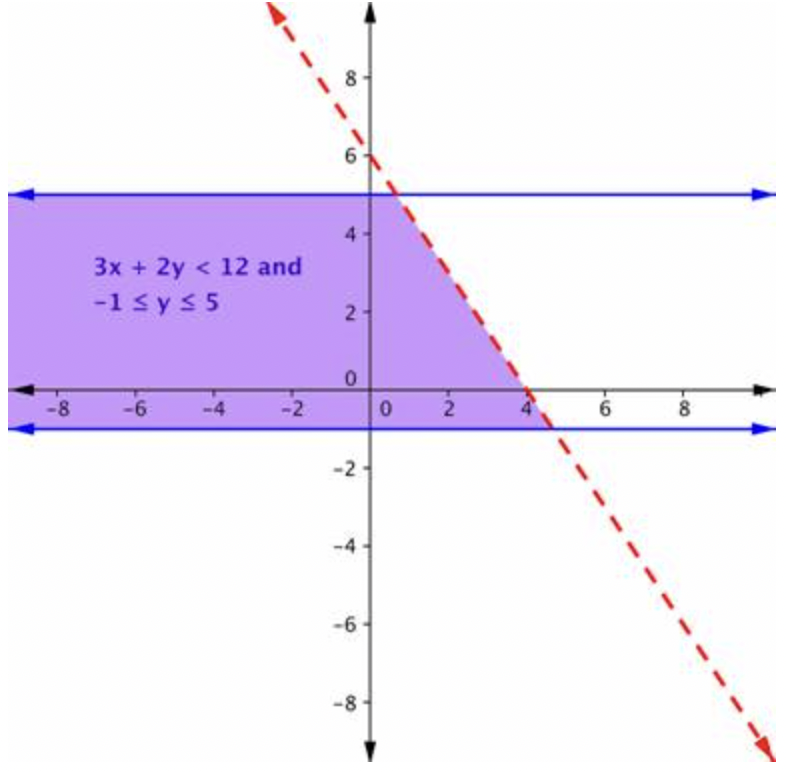
La región púrpura en esta gráfica muestra el conjunto de todas las soluciones del sistema.
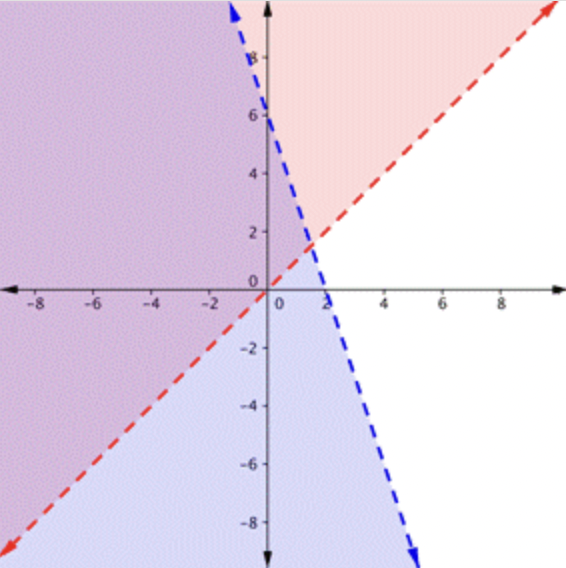
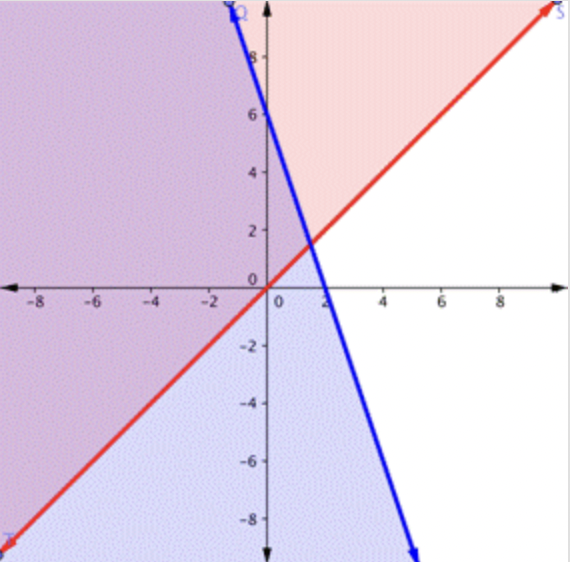
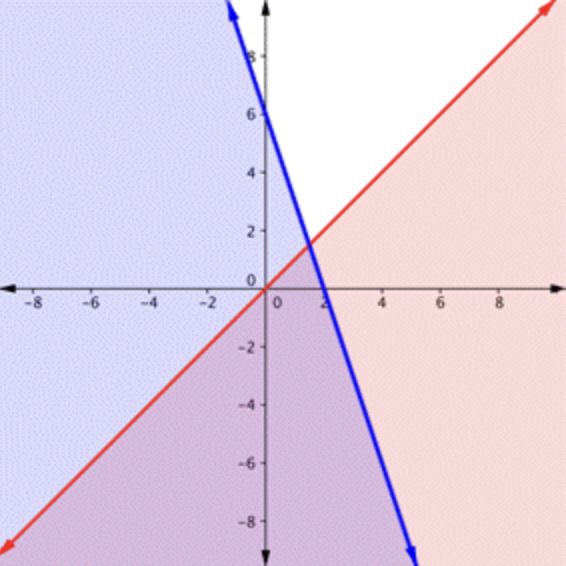
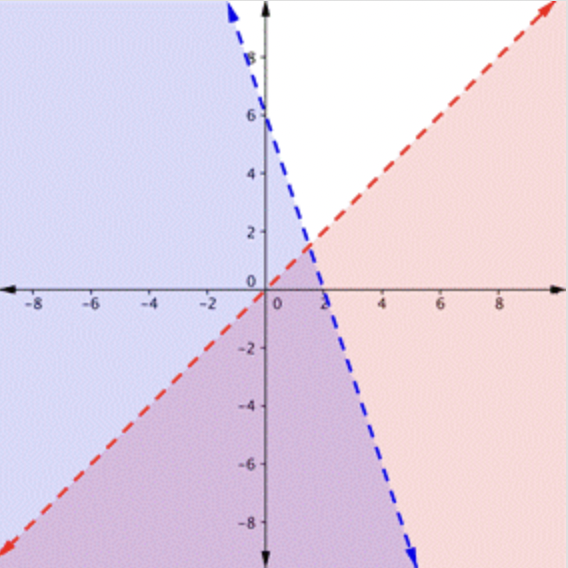
¿En cuál de las siguientes es la región morada la solución para el sistema?
\ (\\ begin {array} {l}
y>x\
y<-3 x+6
\ end {array}\)
- Contestar
-
Graficar un sistema de desigualdades puede ayudarte a resolver situaciones de la vida real.
Cathy está vendiendo conos de helado en una recaudación de fondos escolar. Ella está vendiendo dos tallas: pequeña (que tiene 1 cucharada) y grande (que tiene 2 bolas). Ella sabe que puede sacar un máximo de 70 bolas de helado de su suministro. Ella cobra $3 por un cono pequeño y $5 por un cono grande.
Cathy quiere ganar al menos 120 dólares para retribuir a la escuela. Escribir y graficar un sistema de desigualdades que modele esta situación.
Solución
| \ (\\ comenzar {alineado} s&=\ texto {cono pequeño}\\ l&=\ texto {cono grande} \ final {alineado}\) |
Primero, identificar las variables. Hay dos variables: el número de conos pequeños y el número de conos grandes. |
| \(\ s+2 l \leq 70\) | Escribe la primera ecuación: el número máximo de primicias que pueda dar. Las primicias que tenga disponibles (70) deben ser mayores o iguales al número de bolas para los conos pequeños\(\ (s)\) y los conos grandes\(\ (2 l)\) que vende. |
| \(\ 3 s+5 l \geq 120\) | Escribe la segunda ecuación: la cantidad de dinero que recauda. Ella quiere que la cantidad total de dinero ganado de conos pequeños\(\ (3 s)\) y conos\(\ (5 l)\) grandes sea de al menos 120 dólares. |
| \ (\\ comenzar {alineado} s+2 l&\ leq 70\\ 3 s+5 l&\ geq 120 \ final {alineado}\) |
Escribe el sistema. |
Ahora grafica el sistema. Las variables\(\ x\) y\(\ y\) han sido reemplazadas por\(\ s\) y\(\ l\); graficaron\(\ s\) a lo largo del eje x, y\(\ l\) a lo largo del eje y.
Primero, grafica la región\(\ s+2 l \leq 70\). Grafique la línea límite y luego pruebe puntos individuales para ver qué región sombrear. A continuación se muestra la gráfica.
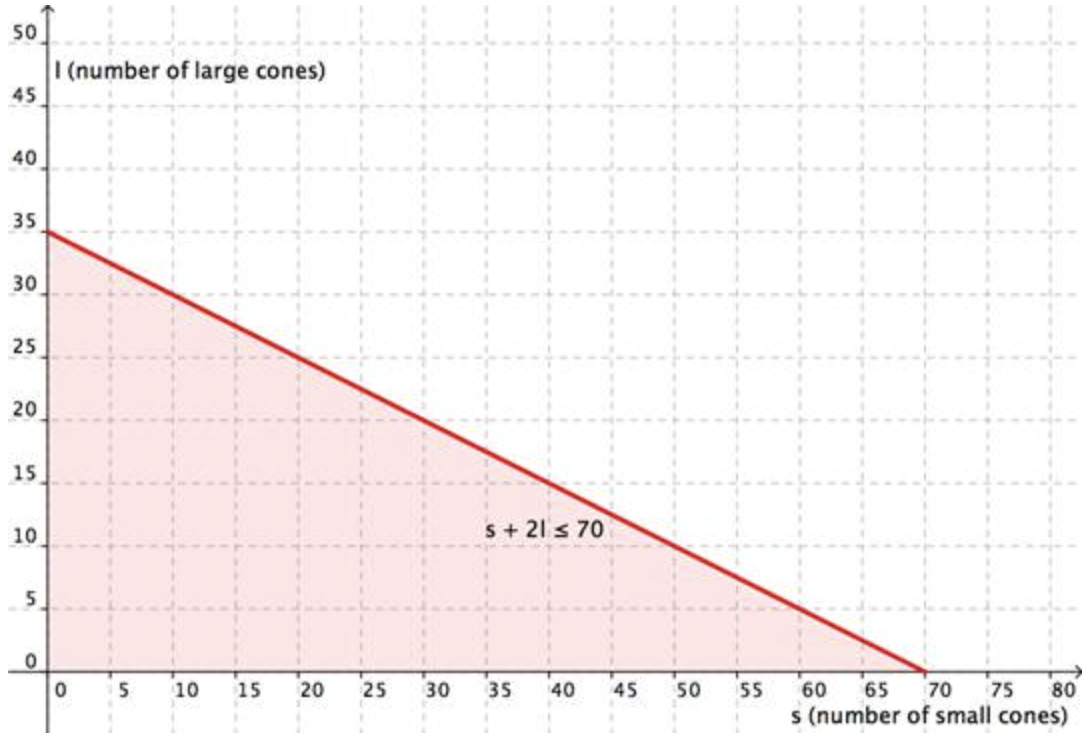
Ahora, grafica la región\(\ 3 s+5 l \geq 120\). Grafique la línea límite y luego pruebe puntos individuales para ver qué región sombrear. A continuación se muestra la gráfica.
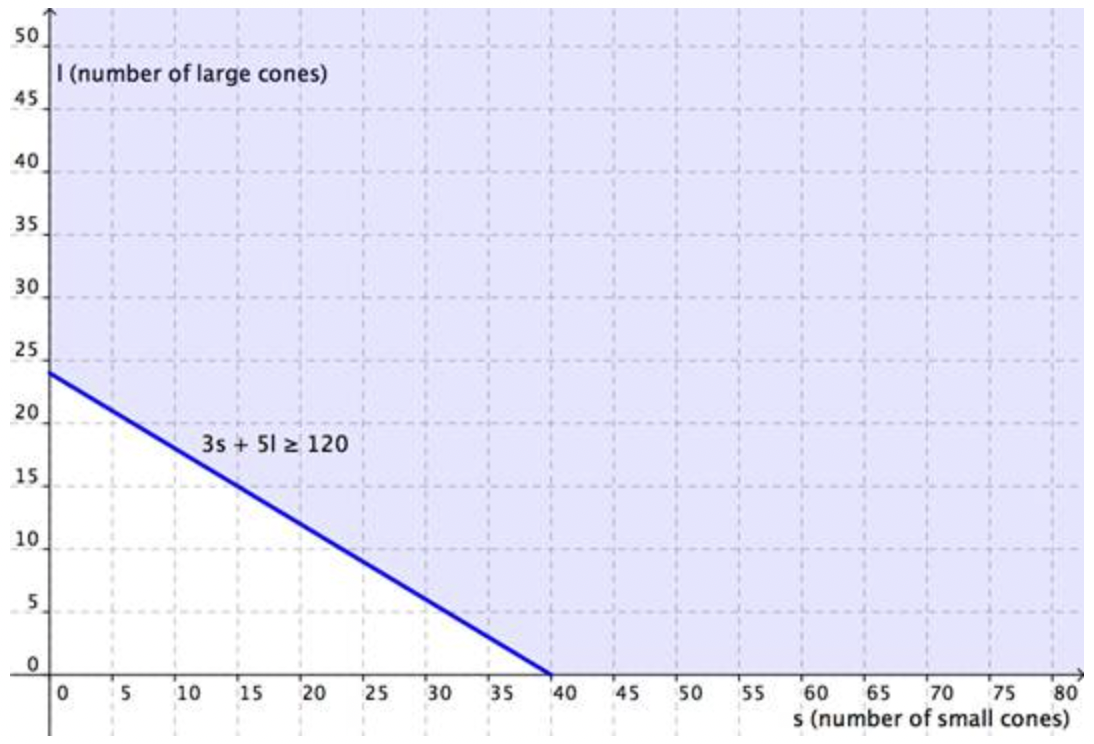
Graficando las regiones juntas, encontrará lo siguiente:
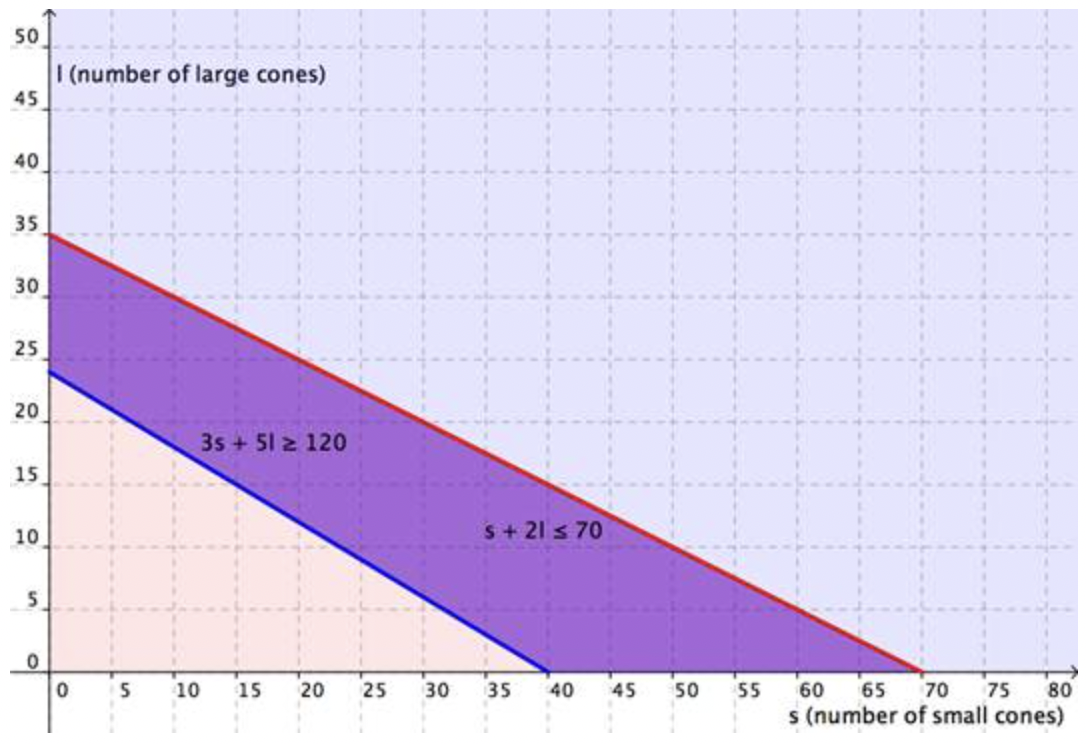
Y representada igual que la región superpuesta, tienes:
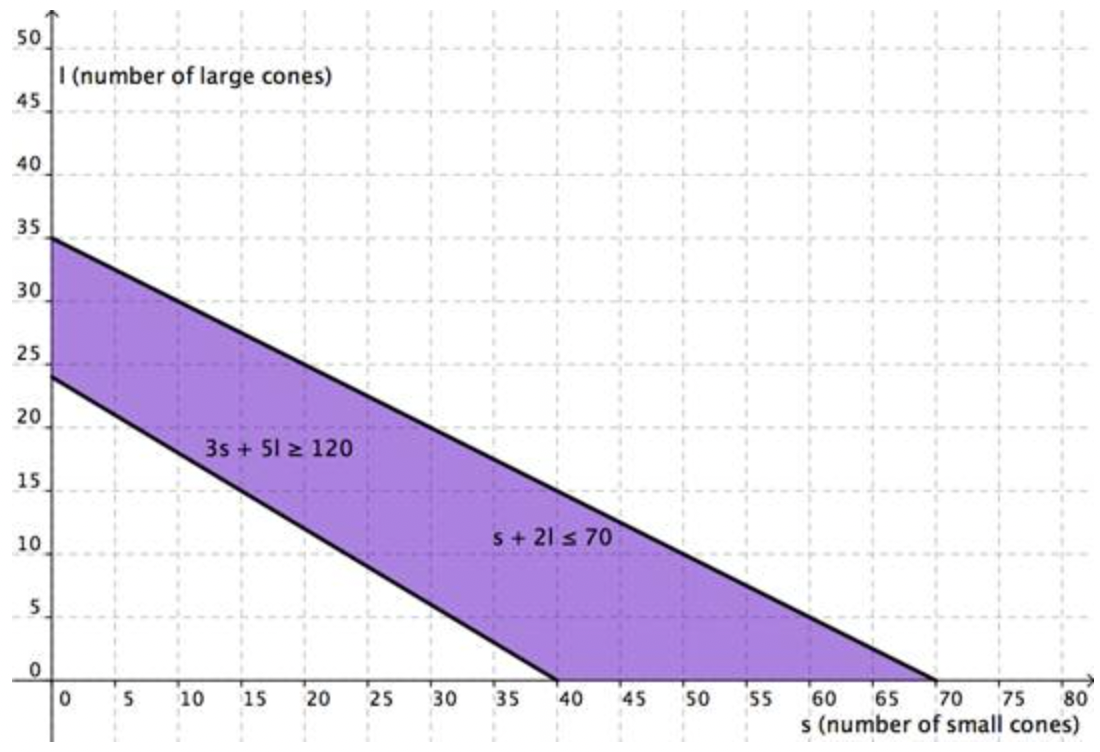
La región en púrpura es la solución. Siempre y cuando la combinación de conos pequeños y conos grandes que vende Cathy pueda mapearse en la región morada, habrá ganado al menos 120 dólares y no habrá usado más de 70 bolas de helado.
Resumen
Los sistemas de desigualdades se pueden graficar en un plano de coordenadas. El conjunto de soluciones para un sistema de desigualdades no es un solo punto, sino una región entera definida por las áreas superpuestas de cada desigualdad individual en el sistema. Cada punto dentro de esta región es una solución a ambas desigualdades y, por lo tanto, una solución para todo el sistema.