14.2.1: El Método de Sustitución
- Page ID
- 111502
- Resolver un sistema de ecuaciones utilizando el método de sustitución.
- Reconocer sistemas de ecuaciones que no tienen solución o un número infinito de soluciones.
- Resolver problemas de aplicación utilizando el método de sustitución.
Introducción
Se puede utilizar una gráfica para mostrar la solución para un sistema de dos ecuaciones lineales. Sin embargo, determinar con precisión la solución a partir de una gráfica no siempre es fácil ni precisa. Por ejemplo, ¿dónde crees que se cruzan las dos líneas que se muestran a continuación?
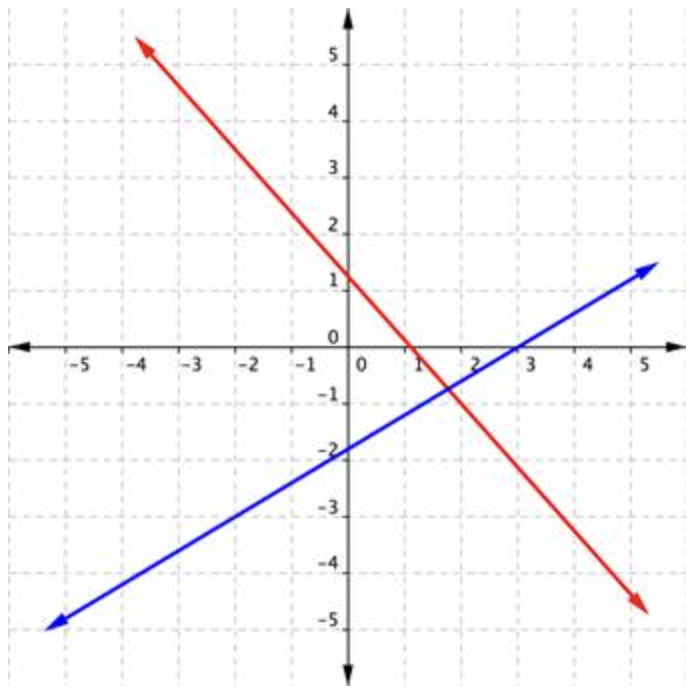
Parece que podrían cruzarse en\(\ (1.8,-0.7)\), aunque esto es sólo una estimación. En casos como este, puedes usar métodos algebraicos para encontrar respuestas exactas. Un método a observar se llama el método de sustitución. Se resuelve una ecuación para una variable y luego se sustituye esta expresión por la otra ecuación.
Uso de la sustitución para resolver un sistema de ecuaciones
En el método de sustitución, se resuelve una variable y luego se sustituye esa expresión en la otra ecuación. Lo importante aquí es que siempre estés sustituyendo valores que sean equivalentes.
Por ejemplo:
Sean es 5 años mayor que cuatro veces la edad de su hija. Su hija tiene 7 años. ¿Cuántos años tiene Sean?
Podrías hacer este problema en tu cabeza. La hija de Sean tiene 7 años, por lo que “cuatro veces la edad de su hija” tiene 28, y 5 años a eso se suman 33. Sean tiene 33 años.
Si resolviste el problema así, usaste una simple sustitución, sustituyó en el valor “7” por “la edad de su hija”. Aprendiste en la segunda parte del problema que “su hija tiene 7 años”. Entonces, sustituir en un valor de “7” por “la edad de su hija” en la primera parte del problema estuvo bien, porque sabías que estas dos cantidades eran iguales.
Veamos un sistema sencillo de ecuaciones que se pueden resolver mediante la sustitución.
Encuentra el valor de\(\ x\) para este sistema.
Ecuación A:\(\ 4 x+3 y=-14\)
Ecuación B:\(\ y=2\)
Solución
| \ (\\ comenzar {alineado} 4 x+3 y&=-14\\ y&=2 \ final {alineado}\) |
El problema pide resolver para\(\ x\). La Ecuación B le da el valor de\(\ y\),\(\ y=2\), por lo que puede sustituir 2 en la Ecuación A por\(\ y\). |
| \(\ 4 x+3(2)=-14\) | Sustituyendo\(\ y=2\) en la Ecuación A. |
| \ (\\ comenzar {alineado} 4 x+6&=-14\\ 4 x&=-20\ x&=-5 \ end {alineado}\) |
Simplificar y resolver la ecuación para\(\ x\). |
\(\ x=-5\)
Puede sustituir un valor por una variable aunque sea una expresión. Aquí tienes un ejemplo.
Resolver para\(\ x\) y\(\ y\).
Ecuación A:\(\ y+x=3\)
Ecuación B:\(\ x=y+5\)
Solución
| \ (\\ begin {array} {l} y+x=3\\ x=y+5 \ end {array}\) |
El objetivo del método de sustitución es reescribir una de las ecuaciones en términos de una sola variable. La ecuación nos\(\ B\) dice eso\(\ x=y+5\), así que tiene sentido sustituirlo\(\ y+5\) en la Ecuación A por\(\ x\). | ||||
| \ (\\ begin {array} {r} y+ {\ color {azul} x} =3\\ y+ {\ color {azul} (y+5)} =3 \ end {array}\) |
Sustituya\(\ y+5\) en la Ecuación A para\(\ x\) y obtienes\(\ y+(y+5)=3\). | ||||
| \ (\\ begin {array} {r} 2 y+5&=\\\ 3\ -5 & -5\\ \ hline 2 y\\\\\\\\ y -2\\ y\\\\\ &=-1 \ end {array}\) |
Simplifica y resuelve la ecuación para obtener\(\ y=-1\). | ||||
| \ (\\ begin {array} {r} y+x&=\\ 3\ -1+x&=\\ 3\ +1\\\\\\\\ &+1\\ \ hline x&=\\ 4 \ end {array}\\) |
Para encontrar ahora\(\ x\), sustituya este valor\(\ y\) en cualquiera de las ecuaciones y resuelva para\(\ x\). Usaremos la Ecuación A aquí para obtener\(\ x=4\). | ||||
|
Finalmente, verifique la solución\(\ x=4\),\(\ y=-1\) sustituyendo estos valores en cada una de las ecuaciones originales. | ||||
| \(\ x=4\)y\(\ y=-1\) | La solución es\(\ (4,-1)\). |
Recuerde, una solución a un sistema de ecuaciones debe ser una solución a cada una de las ecuaciones dentro del sistema. El par ordenado\(\ (4,-1)\) funciona para ambas ecuaciones, así que sabes que también es una solución para el sistema.
Veamos otro ejemplo cuya sustitución involucra la propiedad distributiva.
Resolver para\(\ x\) y\(\ y\).
\ (\\ begin {array} {c}
y=3 x+6\\
-2 x+4 y=4
\ end {array}\)
Solución
| \ (\\ begin {array} {r} y=3 x+6\\ -2 x+4 y=4 \ end {array}\) |
Elija una ecuación para usar para la sustitución. La primera ecuación te dice cómo expresarte\(\ y\) en términos de\(\ x\), por lo que tiene sentido sustituir\(\ 3 x+6\) en la segunda ecuación para\(\ y\). |
||||
| \ (\\ begin {array} {r} -2 x+4 {\ color {azul} y} =4\\ -2 x+4 {\ color {azul} (3 x+6)} =4 \ end {array}\) |
Sustituir\(\ 3 x+6\)\(\ y\) en la segunda ecuación. | ||||
|
\ (\\ comenzar {matriz} {r} |
Simplificar y resolver la ecuación para\(\ x\). | ||||
| \ (\\ begin {array} {r} y=3 x+6\\ y=3 (-2) +6\\ y=-6+6\\ y=0 \ end {array}\) |
Para encontrar\(\ y\), sustituya este valor por de\(\ x\) nuevo en una de las ecuaciones originales. | ||||
|
Verifique la solución\(\ x=-2\),\(\ y=0\) sustituyéndolas en cada una de las ecuaciones originales. |
\(\ x=-2\)y\(\ y=0\).
La solución es\(\ (-2,0)\).
En los ejemplos anteriores, una de las ecuaciones ya nos fue dada en términos de la variable\(\ x\) o\(\ y\). Esto nos permitió sustituir rápidamente ese valor en la otra ecuación y resolver por una de las incógnitas.
A veces es posible que tengas que reescribir una de las ecuaciones en términos de una de las variables primero antes de poder sustituirla. Mira el ejemplo a continuación.
Resolver para\(\ x\) y\(\ y\).
\ (\\ begin {array} {c}
2 x+3 y=22\\
3 x+y=19
\ end {array}\)
Solución
| \ (\\ begin {array} {r} 2 x+3 y=22\\ 3 x+y=19 \ end {array}\) |
Elija una ecuación para usar para la sustitución. La segunda ecuación,\(\ 3 x+y=19\), se puede reescribir fácilmente en términos de\(\ y\), por lo que tiene sentido comenzar ahí. | ||||
| \ (\\ begin {array} {l} 3 x+y=19\\ y=19-3 x \ end {array}\) |
Reescribir\(\ 3 x+y=19\) en términos de\(\ y\). | ||||
| \ (\\ begin {array} {r} 2 x+3 {\ color {azul} y} =22\\ 2 x+3 {\ color {azul} (19-3 x)} =22 \ end {array}\) |
Sustituir\(\ 19-3 x\)\(\ y\) en la otra ecuación como\(\ 2 x+3(19-3 x)=22\). | ||||
| \ (\\ begin {array} {r} 2 x+57-9 x=22\\ -7 x+57=22\\ -7 x=-35\ x=5 \ end {array}\) |
Simplificar y resolver la ecuación para\(\ x\). | ||||
| \ (\\ begin {array} {r} 3 x+y=19\\ 3 (5) +y=19\\ 15+y=19\\ y=19-15\\ y=4 \ end {array}\) |
Sustituya de\(\ x=5\) nuevo en una de las ecuaciones originales para resolver\(\ y\). | ||||
|
Verifique ambas soluciones sustituyéndolas en cada una de las ecuaciones originales. |
\(\ x=5\)y\(\ y=4\)
La solución es\(\ (5,4)\).
Resolver el sistema para\(\ x\) y\(\ y\).
\ (\\ begin {array} {l}
2 y=x+8\\
2 y-10=2 x
\ end {array}\)
- \(\ x=-3, y=2\)
- \(\ x=-2, y=3\)
- \(\ x=-5, y=2\)
- \(\ x=0, y=-5\)
- Contestar
-
- Incorrecto. Si sustitues los valores\(\ x=-3\) y\(\ y=2\) en la primera ecuación, obtienes una declaración falsa:\(\ 2(2)=-3+9\). Para resolver este sistema, intente reescribir la primera ecuación como\(\ x=2 y-8\). Entonces sustituya\(\ 2 y-8\)\(\ x\) en la segunda ecuación, y resuelva para\(\ y\). La respuesta correcta es\(\ x=-2\),\(\ y=3\).
- Correcto. Sustituir estos valores en cualquiera de las ecuaciones da como resultado una declaración verdadera:\(\ 2(3)=-2+8\), y\(\ 2(3)-10=2(-2)\).
- Incorrecto. Si sustitues los valores\(\ x=-5\) y\(\ y=2\) en la segunda ecuación, obtienes una declaración falsa:\(\ 2(2)-10=2(-5)\). Para resolver este sistema, intente reescribir la primera ecuación como\(\ x=2 y-8\). Entonces sustituya\(\ 2 y-8\)\(\ x\) en la segunda ecuación, y resuelva para\(\ y\). La respuesta correcta es\(\ x=-2, y=3\).
- Incorrecto. Si sustitues los valores\(\ x=0\) y\(\ y=-5\) en la segunda ecuación, obtienes una declaración falsa:\(\ 2(-5)-10=2(0)\). Para resolver este sistema, intente reescribir la primera ecuación como\(\ x=2 y-8\). Entonces sustituya\(\ 2 y-8\)\(\ x\) en la segunda ecuación, y resuelva para\(\ y\). La respuesta correcta es\(\ x=-2, y=3\).
Situaciones Especiales
Hay algunos casos en los que el uso del método de sustitución dará resultados que, al principio, no tienen sentido. Echemos un vistazo a algunos de estos y descubramos qué está pasando.
Resolver para\(\ x\) y\(\ y\).
\ (\\ begin {array} {c}
y=5 x+4\\
10 x-2 y=4
\ end {array}\)
Solución
|
\ (\\ begin {array} {r} \(\ 10 x-2\color{blue}(5 x+4)=4\) |
Dado que la primera ecuación es\(\ y=5 x+4\), se puede sustituir\(\ 5 x+4\)\(\ y\) en la segunda ecuación. |
| \(\ 10 x-10 x-8=4\) | Expande la expresión a la izquierda. |
| \ (\\ comenzar {alineado} 0-8 &=4\\ -8 &=4 \ end {alineado}\) |
Combina términos similares en el lado izquierdo de la ecuación. \(\ 10 x-10 x=0\), así que te quedas con\(\ -8=4\). |
El enunciado\(\ -8=4\) es falso, por lo que no hay solución.
Obtienes la declaración falsa\(\ -8=4\). ¿Qué significa esto? El gráfico de este sistema arroja algo de luz sobre lo que está sucediendo.
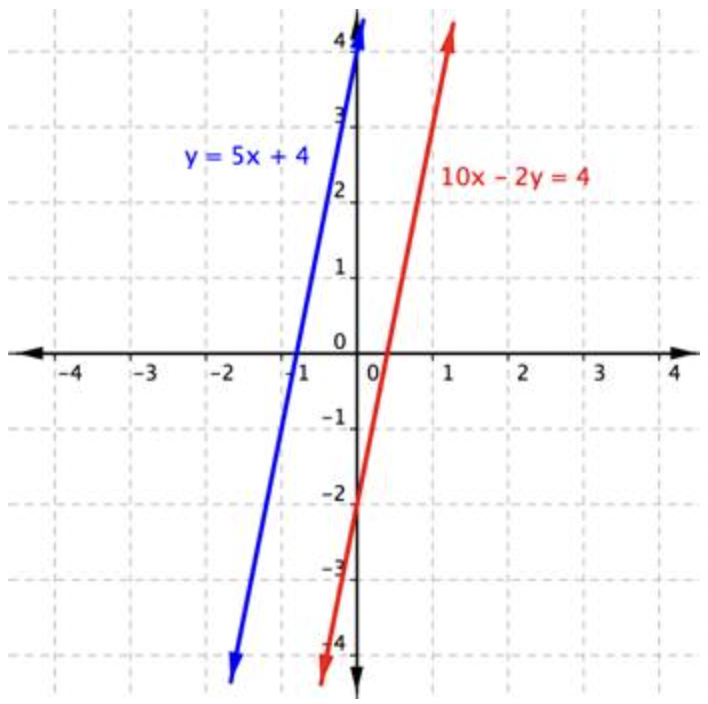
Las líneas son paralelas. Nunca se cruzan y no hay solución a este sistema de ecuaciones lineales. Tenga en cuenta que el resultado no\(\ -8=4\) es una solución. Es simplemente una declaración falsa e indica que no hay solución.
Ahora toma este problema, que también es interesante.
\ (\\ begin {array} {c}
\ color {verde}\ texto {Resolver para} x\ texto {y} y.
\\ color {verde} y=-0.5x\
\ color {verde} 9y=-4.5x
\ end {array}\)
Sustituyendo\(\ -0.5 x\)\(\ y\) en la segunda ecuación, se encuentra lo siguiente:
\ (\\ comenzar {alineado}
9 y &=-4.5 x\\
9 (-0.5 x) &=-4.5 x\\
-4.5 x &=-4.5 x
\ end {alineado}\)
Esta vez, se obtiene una verdadera declaración:\(\ -4.5 x=-4.5 x\). Pero, ¿qué significa este tipo de respuesta? Nuevamente, la gráfica puede ayudarte a darle sentido a este sistema.
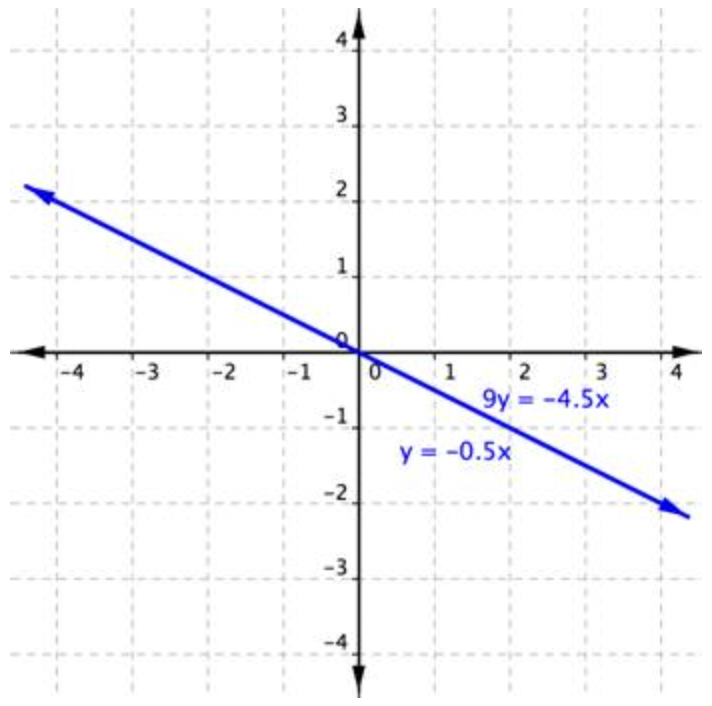
Este sistema consta de dos ecuaciones que ambas representan la misma línea; las dos líneas son colineales. Cada punto a lo largo de la línea será una solución para el sistema, y es por eso que el método de sustitución produce una declaración verdadera. En este caso, hay un número infinito de soluciones.
Aubrey está utilizando el método de sustitución para resolver el siguiente sistema de ecuaciones:
\ (\\ begin {array} {l}
y-x=21\\
2 y=2 x+16
\ end {array}\)
Ella llega a una respuesta de\(\ 8=21\). Ella piensa que esta respuesta significa que las líneas son paralelas y que el sistema no tiene solución.
Aubrey quiere comprobar su respuesta. ¿Cuál de las siguientes acciones la ayudará mejor a averiguar si las dos ecuaciones del sistema son, de hecho, paralelas?
- Verifique si las pendientes de ambas líneas son las mismas, y las intercepciones en Y son diferentes.
- Verifique si alguna de las líneas pasa por el origen.
- Verifique si las líneas tienen la misma intersección en Y.
- Comprueba si ambas líneas pasan por el punto\(\ (8,21)\).
- Contestar
-
- Correcto. Las líneas paralelas tienen la misma pendiente, pero también tiene que verificar si tienen diferentes intercepciones y porque las líneas podrían ser colineales (recuerde que 2 líneas colineales son la misma línea). Si Aubrey encuentra que las pendientes de las líneas son las mismas y las intercepciones en Y son diferentes, entonces puede estar segura de que su respuesta es correcta.
- Incorrecto. El origen no tiene relación con si dos líneas son paralelas. En el caso de este sistema, ninguna línea pasa por el origen, sino que las líneas siguen siendo paralelas. Si Aubrey encuentra que las pendientes de las líneas son las mismas y las intercepciones en Y son diferentes, entonces puede estar segura de que su respuesta es correcta.
- Incorrecto. Es cierto que las líneas con la misma intersección y nunca son paralelas, porque las líneas paralelas nunca pueden cruzarse. Pero con solo comprobar que las intercepciones y no son lo mismo no es suficiente. Para ser paralelas, las líneas también deben tener la misma pendiente. Si Aubrey encuentra que las pendientes de las líneas son las mismas y las intercepciones en Y son diferentes, entonces puede estar segura de que su respuesta es correcta.
- Incorrecto. A pesar de que llegó a una respuesta de\(\ 8=21\), esto no quiere decir que las propias líneas se crucen en ese punto\(\ (8,21)\). Si Aubrey encuentra que las pendientes de las líneas son las mismas y las intercepciones en Y son diferentes, entonces puede estar segura de que su respuesta es correcta.
Resolviendo problemas de aplicación mediante sustitución
Los sistemas de ecuaciones son una herramienta muy útil para modelar situaciones de la vida real y responder preguntas sobre ellas. Si puedes traducir la aplicación en dos ecuaciones lineales con dos variables, entonces tienes un sistema de ecuaciones que puedes resolver para encontrar la solución. Se puede utilizar cualquier método para resolver el sistema de ecuaciones. Utilice el método de sustitución en este tema.
Para vender más de sus productos, una granja local vende bolsas de manzanas en dos tamaños: mediano y grande. Una bolsa mediana contiene 4 manzanas Macintosh y 1 Granny Smith y cuesta $2.80. Una bolsa grande contiene 8 manzanas Macintosh y 4 Granny Smith y cuesta $7.20. El precio de una manzana Granny Smith es el mismo en la bolsa mediana que en la bolsa grande. El precio de una manzana Macintosh es el mismo en la bolsa mediana que en la bolsa grande. ¿Cuál es el precio de cada tipo de manzana?
Empecemos por crear un sistema de ecuaciones que represente lo que está sucediendo en el problema. Hay dos tipos de manzanas y dos tamaños de bolsas. Puedes dejar\(\ m\) representar el costo de una manzana Macintosh y\(\ g\) representar el costo de una manzana Granny Smith. Hagamos una mesa y veamos lo que se sabe.
| Costo de las manzanas Macintosh | + | Costo de las manzanas Granny Smith | = | Costo total de la bolsa | |
| Mediano | \(\ 4m\) | + | \(\ g\) | = | $2.80 |
| Grande | \(\ 8m\) | + | \(\ 4g\) | = | $7.20 |
Ahora que tienes dos ecuaciones en las mismas variables, puedes resolver el sistema. Usarás la sustitución. Los pasos se muestran en el siguiente ejemplo:
Resolver\(\ g\) y\(\ m\) usar el método de sustitución.
\ (\\ begin {array} {c}
4 m+g=2.80\\
8 m+4 g=7.20
\ end {array}\)
Solución
| \ (\\ begin {array} {l} 4 m+g=2.80\\ g=2.80-4 m \ end {array}\) |
Primero, reescribir una de las ecuaciones en términos de una de las variables. |
| \ (\\ comenzar {array} {r} 8 m+4\ color {azul} g=7.20\\ 8 m+4\ color {azul} (2.80-4 m) =7.20\\ 8 m+11.20-16 m=7.20\\ 8 m-16 m=7.20-11.20\ -8 m=-4.00\ m=0.50 \ end {array}\) |
Sustituir\(\ (2.80-4 m)\)\(\ g\) en la segunda ecuación y resolver para\(\ m\). |
| \ (\\ begin {array} {r} 4 m+g=2.80\\ 4 (0.5) +g=2.80\\ 2+g=2.80\\ g=2.80-2\\ g=0.80 \ end {array}\) |
Sustituir el valor de\(\ m\)\(\ 0.50\),, en una de las ecuaciones originales para resolver\(\ g\). |
| \ (\\ comenzar {alineado} 4 m+g &=2.80\\ 4 (.50) +.80 &=2.80\\ 2.80 &=2.80 \ end {alineado}\) |
Verifique ambas ecuaciones sustituyendo los valores de\(\ g\) y\(\ m\). |
| \ (\\ comenzar {alineado} 8 m+4 g &=7.20\\ 8 (.50) +4 (.80) &=7.20\\ 4.00+3.20 &=7.20\\ 7.20 &=7.20 \ end {alineado}\) |
Una manzana Granny Smith cuesta $0.80 y una manzana Macintosh cuesta $0.50.
El uso del método de sustitución puede ser un enfoque efectivo para resolver problemas geométricos.
El perímetro de un rectángulo es de 60 pulgadas. Si el largo es 10 pulgadas más largo que el ancho, busque las dimensiones usando el método de sustitución.
Solución
| \ (\\ begin {array} {r} 2 l+2 w=60\\ l=w+10 \ end {array}\) |
Utilice la información proporcionada para escribir un sistema de ecuaciones. Dejar\(\ l=\text { length }\) y\(\ w=\text { width }\). |
| \ (\\\ begin {array} {r} 2 {\ color {azul} l}\\\\\\\\\\ +2 w&=\\ 60\\ 2 {\ color {azul} (w+10)} +2 w & =\\ 60\\ 2 w\\\ +20\\\\ +2 w & =\\\ 60\\ 4 w\\\ +20&=\ \\ 60\\ -20 & -20\\ \ hline 4 w&=\\\ 40\ w&=\\\ 10 \ end {array}\) |
Sustituir\(\ w+10\)\(\ l\) en la primera ecuación y resolver para\(\ w\). |
| \ (\\ begin {array} {r} l=w+10\\ l=10+10\\ l=20 \ end {array}\) |
Para encontrar\(\ l\), sustituir 10\(\ w\) en una de las ecuaciones y resolver para\(\ l\). |
| \ (\\ begin {array} {r} l=w+10\\ 20=10+10\\ 20=20 \ end {array}\) |
Verifique ambas soluciones sustituyéndolas en las dos ecuaciones. |
| \ (\\ begin {array} {r} 2 l+2 w=60\\ 2 (20) +2 (10) =60\\ 40+20=60\\ 60=60 \ end {array}\) |
Ambos son ciertos, por lo que esta es una solución correcta. |
La longitud del rectángulo es de 20 pulgadas.
El ancho del rectángulo es de 10 pulgadas.
Resumen
El método de sustitución es una forma de resolver sistemas de ecuaciones. Para utilizar el método de sustitución, utilice una ecuación para encontrar una expresión para una de las variables en términos de la otra variable. Después sustituya esa expresión en lugar de esa variable en la segunda ecuación. Entonces puedes resolver esta ecuación ya que ahora solo tendrá una variable. Resolver usando el método de sustitución arrojará uno de tres resultados: un solo valor para cada variable dentro del sistema (indicando una solución), una declaración falsedad (que indica que no hay soluciones) o una declaración verdadera (que indica un número infinito de soluciones).


