14.2.2: El Método de Eliminación
- Page ID
- 111503
- Resuelve un sistema de ecuaciones cuando no es necesaria la multiplicación para eliminar una variable.
- Resuelve un sistema de ecuaciones cuando la multiplicación es necesaria para eliminar una variable.
- Reconocer sistemas que no tienen solución o un número infinito de soluciones.
- Resolver problemas de aplicación utilizando el método de eliminación.
Introducción
El método de eliminación para resolver sistemas de ecuaciones lineales utiliza la propiedad de suma de igualdad. Se puede agregar el mismo valor a cada lado de una ecuación.
Entonces, si tienes un sistema:\(\ x-y=-6\) y\(\ x+y=8\), puedes agregar\(\ x+y\) al lado izquierdo de la primera ecuación y sumar 8 al lado derecho de la ecuación. Y ya que\(\ x+y=8\), estás agregando el mismo valor a cada lado de la primera ecuación.
Uso de la adición para eliminar una variable
Si se suman las dos ecuaciones,\(\ x-y=-6\) y\(\ x+y=8\) juntas, como se señaló anteriormente, observe lo que sucede.
\ (\\ begin {array} {rr}
x-y= & -6\
x+y= & 8\\
\ hline 2 x+0= & 2
\ end {array}\)
Se ha eliminado el\(\ y\) término, y esta ecuación se puede resolver utilizando los métodos para resolver ecuaciones con una variable.
Veamos cómo se resuelve este sistema utilizando el método de eliminación.
Utilice la eliminación para resolver el sistema.
\ (\\ begin {array} {c}
x-y=-6\
x+y=8
\ end {array}\)
Solución
| \ (\\ begin {array} {r} x-y= & -6\\ +\ quad x+y= & 8\\ \ hline 2 x\\\\\\ = &2 \ end {array}\\) |
Sumar las ecuaciones. | ||||
| \ (\\ comenzar {alineado} 2 x &=2\\ x &=1 \ end {alineado}\) |
Resolver para\(\ x\). | ||||
| \ (\\ begin {array} {r} x+y=8\\ 1+y=8\\ y=8-1\ y=7 \ end {array}\) |
Sustituya\(\ x=1\) en una de las ecuaciones originales y resuelva para\(\ y\). | ||||
|
¡Asegúrate de verificar tu respuesta en ambas ecuaciones! Las respuestas verifican. |
La solución es\(\ (1,7)\).
Desafortunadamente, no todos los sistemas funcionan esto fácilmente. ¿Qué tal un sistema como\(\ 2 x+y=12\) y\(\ -3 x+y=2\)? Si se suman estas dos ecuaciones juntas, no se eliminan variables.
\ (\\ comenzar {alineado}
2 x+y&=12\\
-3 x+y&=2\
\ hline-x+2 y&=14
\ end {alineado}\)
Pero se quiere eliminar una variable. Entonces agreguemos lo contrario de una de las ecuaciones a la otra ecuación.
\ (\\ begin {array} {r}
2 x+y=12\ quad\ fila derecha& 2 x+y=12\ quad\ fila derecha&\ quad 2 x+y=\ 12\
-3 x+y=2\ quad\ fila derecha&- (-3 x+y) =- (2)\ quad\ derecha&\ quad\ subrayado {3x-y=-2}\
&& 5x+0y=\ 10
\ end {array}\)
Se ha eliminado la\(\ y\) variable, y el problema ya se puede resolver. Vea el ejemplo a continuación.
Utilice la eliminación para resolver el sistema.
\ (\\ comenzar {alineado}
2 x+y&=12\\
-3 x+y&=2
\ final {alineado}\)
Solución
| \ (\\ comenzar {alineado} 2 x+y&=12\\ -3 x+y&=2 \ final {alineado}\) |
Puede eliminar la variable y si agrega lo contrario de una de las ecuaciones a la otra ecuación. | ||||
| \ (\\ comenzar {alineado} 2 x+y&=12\\ 3 x-y&=-2\\ 5 x&=10 \ end {alineado}\) |
Reescribe la segunda ecuación como su opuesto. Agregar. |
||||
| \(\ x=2\) | Resolver para\(\ x\). | ||||
| \ (\\ begin {array} {r} 2 (2) +y=12\\ 4+y=12\\ y=8 \ end {array}\) |
Sustituya\(\ x=2\) en una de las ecuaciones originales y resuelva para\(\ y\). | ||||
|
¡Asegúrate de verificar tu respuesta en ambas ecuaciones! Las respuestas verifican. |
La solución es\(\ (2,8)\).
A continuación se presentan dos ejemplos más que muestran cómo resolver sistemas lineales de ecuaciones mediante eliminación.
Utilice la eliminación para resolver el sistema.
\ (\\ comenzar {alineado}
-2 x+3 y&=-1\\
2 x+5 y&=25
\ final {alineado}\)
Solución
| \ (\\ comenzar {alineado} -2 x+3 y &=-1\\ 2 x+5 y &=25 \ final {alineado}\) |
Observe los coeficientes de cada variable en cada ecuación. Si agrega estas dos ecuaciones, el\(\ x\) término será eliminado desde entonces\(\ -2 x+2 x=0\). | ||||
| \ (\\ begin {array} {rr} -2 x+3 y= & -1\\ 2 x+5 y= & 25\ \ hline 8 y= & 24\\ y= & 3 \ end {array}\) |
Agregar y resolver para\(\ y\). | ||||
| \ (\\ comenzar {alineado} 2 x+5 y&=25\\ 2 x+5 (3) &=25\\ 2 x+15&=25\\ 2 x&=10\\ x&=5 \ end {alineado}\) |
Sustituir\(\ y=3\) en una de las ecuaciones originales. | ||||
|
Revisar soluciones. Las respuestas verifican. |
La solución es\(\ (5,3)(5,3)\).
Utilice la eliminación para resolver para\(\ x\) y\(\ y\).
Solución
| \ (\\ begin {array} {l} 4 x+2 y=14\\ 5 x+2 y=16 \ end {array}\) |
Observe los coeficientes de cada variable en cada ecuación. Se necesitará agregar lo contrario de una de las ecuaciones para eliminar la variable\(\ y\), as\(\ 2 y+2 y=4 y\), pero\(\ 2 y+(-2 y)=0\). |
| \ (\\ begin {array} {r} 4 x+2 y= & 14\\ -5 x-2 y= & -16\\ \ hline-x\\\\\\\\\ = & -2\\ x\\\\\\\\\ = & 2 \ end {array}\\) |
Cambiar una de las ecuaciones a su opuesto, sumar y resolver para\(\ x\). |
| \ (\\ comenzar {alineado} 4 x+2 y=&14\\ 4 (2) +2 y=&14\\ 8+2 y=&14\\ 2 y=&6\\ y=&3 \ end {alineado}\) |
Sustituya\(\ x=2\) en una de las ecuaciones originales y resuelva para\(\ y\). |
La solución es\(\ (2,3)\).
Sigue adelante y revisa este último ejemplo—sustituirlo\(\ (2,3)\) en ambas ecuaciones. Obtienes dos afirmaciones verdaderas:\(\ 16=16\) ¡\(\ 14=14\)y!
Observe que podría haber usado lo contrario de la primera ecuación en lugar de la segunda ecuación y haber obtenido el mismo resultado.
Uso de Multiplicación y Adición para Eliminar Variables
Muchas veces, sumar las ecuaciones o sumar lo contrario de una de las ecuaciones no resultará en eliminar una variable. Mira el sistema a continuación.
\ (\\ comenzar {alineado}
3 x+4 y=52\\
5 x+y=30
\ final {alineado}\)
Si agrega las ecuaciones anteriores, o agrega lo contrario de una de las ecuaciones, obtendrá una ecuación que aún tiene dos variables. Entonces usemos ahora primero la propiedad de multiplicación de la igualdad. Se pueden multiplicar ambos lados de una de las ecuaciones por un número que dará como resultado que el coeficiente de una de las variables sea el opuesto de la misma variable en la otra ecuación.
Aquí es donde la multiplicación viene muy bien. La primera ecuación contiene el término\(\ 4y\) y la segunda ecuación contiene el término\(\ y\). Si multiplicas la segunda ecuación por -4, al sumar ambas ecuaciones, las\(\ y\) variables sumarán hasta 0.
\ (\\ comenzar {array} {l}
3 x+4 y=52\ cuadridad&\ fila derecha\ cuádruple x+4 y=52\ cuadrilátero\ cuadriculo&derecha3 x+4 y= 52\\
5 x+y=30\ cuadridad&\ fila derecha\ cuadriculo-4 (5 x+y) =-4 (30)\ cuadrilátero\ cuadriculado\ subrayado {-20 x-4 y=-120}\\
&&\ quad-17x+0y=-68
\ end {array}\)
Vea el ejemplo a continuación.
Resolver para\(\ x\) y\(\ y\).
Ecuación A:\(\ 3 x+4 y=52\)
Ecuación B:\(\ 5 x+y=30\)
Solución
| \ (\\ begin {array} {r} 3 x+4 y=52\\ 5 x+\\ y=30 \ end {array}\) |
Busca términos que puedan ser eliminados. Las ecuaciones no tienen ninguno\(\ x\) o\(\ y\) términos con los mismos coeficientes. | ||||
| \ (\\ comenzar {alineado} 3 x+4 y&=52\\ -4 (5 x+y) &=-4 (30)\\ \ hline \ final {alineado}\) |
Multiplique la segunda ecuación por -4 para que tengan el mismo coeficiente. | ||||
| \ (\\ begin {array} {rr} 3 x+4 y= & 52\\ -20 x-4 y= & -120\ \ hline \ end {array}\) |
Reescribe el sistema y agrega las ecuaciones. | ||||
| \ (\\ comenzar {alineado} -17 x &=-68\\ x &=4 \ final {alineado}\) |
Resolver para\(\ x\). | ||||
| \ (\\ begin {array} {r} 3 x+4 y=52\\ 3 (4) +4 y=52\\ 12+4 y=52\\ 4 y=40\ y=10 \ end {array}\) |
Sustituir\(\ x=4\) en una de las ecuaciones originales para encontrar\(\ y\). | ||||
|
Comprueba tu respuesta. Las respuestas verifican. |
La solución es\(\ (4,10)\).
Hay otras formas de resolver este sistema. En lugar de multiplicar una ecuación para eliminar una variable cuando se agregaron las ecuaciones, podrías haber multiplicado ambas ecuaciones por diferentes números.
Eliminemos la variable\(\ x\) esta vez. Multiplica la Ecuación A por 5 y la Ecuación B por -3.
Resolver para\(\ x\) y\(\ y\).
\ (\\ begin {array} {r}
3 x+4 y=52\\
5 x+\\ y=30
\ end {array}\)
Solución
| \ (\\ begin {array} {r} 3 x+4 y=52\\ 5 x+\\ y=30 \ end {array}\) |
Busca términos que puedan ser eliminados. Las ecuaciones no tienen ninguno\(\ x\) y\(\ y\) términos con el mismo coeficiente. |
|
\ (\\ comenzar {alineado} \ (\\ comenzar {alineado} |
Para usar el método de eliminación, hay que crear variables que tengan el mismo coeficiente, entonces puede eliminarlas. Multiplica la ecuación superior por 5. |
|
\ (\\ comenzar {alineado} \ (\\ begin {array} {r} |
Ahora multiplica la ecuación inferior por -3. |
| \ (\\ begin {array} {r} 15 x+20 y &=&+260\\ -15 x-\\ 3 y &=&- 90\ \ hline 17 y &=& 170\\ y &=& 10 \ end {array}\) |
A continuación, agregue las ecuaciones, y resuelva para\(\ y\). |
| \ (\\ comenzar {alineado} 3 x+4 y&=52\\ 3 x+4 (10) &=52\\ 3 x+40&=52\\ 3 x&=12\\ x&=4 \ end {alineado}\) |
Sustituir\(\ y=10\) en una de las ecuaciones originales para encontrar\(\ x\). |
| La solución es\(\ (4,10)\). | Se llega a la misma solución que antes. |
Estas ecuaciones se multiplicaron por 5 y -3 respectivamente, porque eso le dio términos que sumarían 0. Asegúrese de multiplicar todos los términos de la ecuación.
Félix necesita encontrar\(\ x\) y\(\ y\) en el siguiente sistema.
Ecuación A:\(\ 7 y-4 x=5\)
Ecuación B:\(\ 3 y+4 x=25\)
Si quiere utilizar el método de eliminación para eliminar una de las variables, ¿cuál es la forma más eficiente para que lo haga?
- Agregar Ecuación A y Ecuación B
- Agregar\(\ 4x\) a ambos lados de la Ecuación A
- Multiplicar la Ecuación A por 5
- Multiplicar la Ecuación B por -1
- Contestar
-
- Correcto. Si Félix suma las dos ecuaciones, los términos\(\ 4x\) y\(\ -4 x\) cancelará, dejando\(\ 10 y=30\). Félix será entonces fácilmente capaz de resolver para\(\ y\).
- Incorrecto. Agregar\(\ 4 x\) a ambos lados de la Ecuación A no cambiará el valor de la ecuación, ni ayudará a eliminar ninguna de las variables; Felix terminará con la ecuación reescrita\(\ 7 y=5+4 x\). La respuesta correcta es agregar la Ecuación A y la Ecuación B.
- Incorrecto. Multiplicando la Ecuación A por 5 rendimientos\(\ 35 y-20 x=25\), lo que no ayuda a Felix a eliminar ninguna de las variables del sistema. Félix puede notar que ahora ambas ecuaciones tienen una constante de 25, pero restar una de otra no es una manera eficiente de resolver este problema. En cambio, crearía otra ecuación donde ambas variables estén presentes. La respuesta correcta es agregar la Ecuación A y la Ecuación B.
- Incorrecto. Multiplicando la Ecuación B por -1 rendimientos\(\ -3 y-4 x=-25\), lo que no ayuda a Felix a eliminar ninguna de las variables del sistema. Félix puede notar que ahora ambas ecuaciones tienen un término de\(\ -4 x\), pero agregarlas no las eliminaría, le daría un\(\ -8 x\). La respuesta correcta es agregar la Ecuación A y la Ecuación B.
Situaciones Especiales
Al igual que con el método de sustitución, el método de eliminación a veces eliminará ambas variables, y terminas con una declaración verdadera o una declaración falsa. Recordemos que una declaración falsa significa que no hay solución.
Veamos un ejemplo.
Resolver para\(\ x\) y\(\ y\).
\ (\\ begin {array} {c}
-x-y=-4\
x+y=2
\ end {array}\)
Solución
| \ (\\ begin {array} {r} -x-y&=&-4\ x+y&=&2\ \ hline 0&=&-2 \ end {array}\) |
Agrega las ecuaciones para eliminar el término x. |
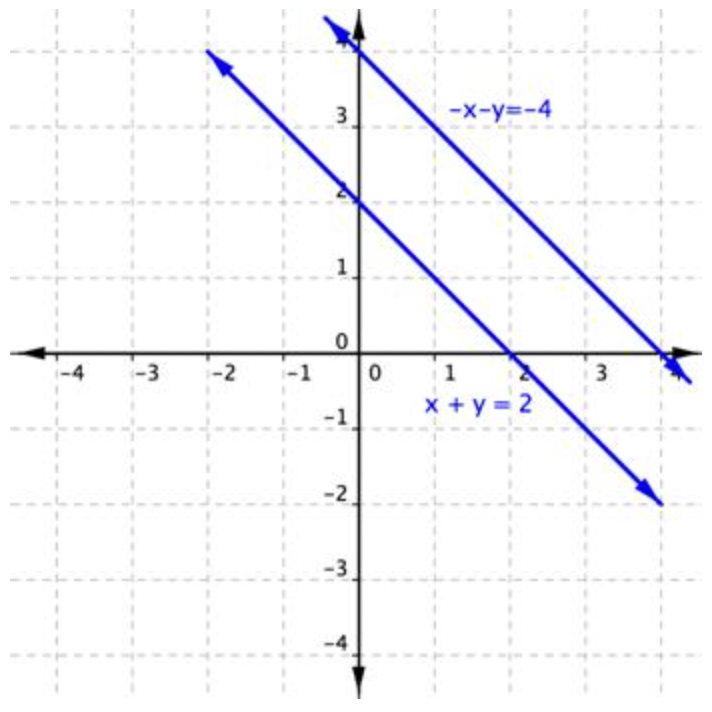
No hay solución.
Graficar estas líneas muestra que son líneas paralelas y como tales no comparten ningún punto en común, verificando que no hay solución.
Si se eliminan ambas variables y te quedas con una declaración verdadera, esto indica que hay un número infinito de pares ordenados que satisfacen ambas ecuaciones. De hecho, las ecuaciones son la misma línea.
Resolver para\(\ x\) y\(\ y\).
\ (\\ begin {array} {r}
x+y&=&2\\
-x-y&=&-2
\ end {array}\)
Solución
| \ (\\ begin {array} {r} x+y&=&2\\ -x-y&=&-2\ \ hline 0&=&0 \ end {array}\) |
Agrega las ecuaciones para eliminar el término x. |
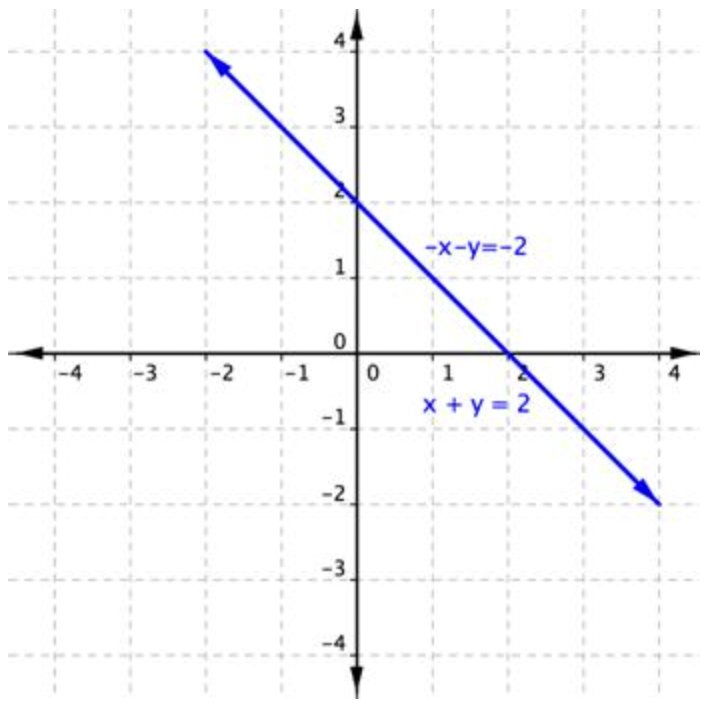
Hay un número infinito de soluciones.
Graficar estas dos ecuaciones ayudará a ilustrar lo que está sucediendo.
Resolver problemas de aplicación usando el método de eliminación
El método de eliminación se puede aplicar a la resolución de sistemas de ecuaciones que modelan situaciones reales. A continuación se muestran dos ejemplos del uso del método de eliminación en la resolución de problemas.
La suma de dos números es 10. Su diferencia es 6. ¿Cuáles son los dos números?
Solución
| \ (\\ begin {array} {r} x+y&=&10\ x-y&=&6 \ end {array}\) |
Escribir un sistema de ecuaciones para modelar la situación. \(\ x\)=un número \(\ y\)=el otro número |
||||
| \ (\\ begin {array} {r} x+y &=&10\\ +\ quad x-y &=&6\\ \ hline 2 x &=&16\\ x &=&8 \ end {array}\) |
Agrega las ecuaciones para eliminar el término y y luego resolver para\(\ x\). | ||||
| \ (\\ begin {array} {r} x+y&=&10\\ 8+y&=&10\ y&=&2 \ end {array}\) |
Sustituir el valor por\(\ x\) en una de las ecuaciones originales para encontrar\(\ y\). | ||||
|
Verifique su respuesta sustituyendo\(\ x=8\) y\(\ y=2\) en el sistema original. Las respuestas verifican. |
Los números son 8 y 2.
Un teatro vendió 800 boletos para la actuación del viernes por la noche. Un boleto infantil cuesta $4.50 y un boleto de adulto cuesta $6.00. El monto total recaudado fue de $4,500. ¿Cuántos de cada tipo de boleto se vendieron?
Solución
|
El número total de boletos vendidos es\(\ 800\). \(\ a+c=800\) La cantidad de dinero recaudado es\(\ $4,500\) \(\ 6 a+4.5 c=4,500\) Sistema de ecuaciones: \(\ a+c=800\) \(\ 6 a+4.5 c=4,500\) |
Escribir un sistema de ecuaciones para modelar la situación de venta de boletos. \(\ a\)=número de boletos para adultos vendidos \(\ c\)=número de boletos infantiles vendidos |
||||
|
\ (\\ begin {array} {r} \ (\\ begin {array} {r} |
Usa la multiplicación para reescribir la primera ecuación. | ||||
|
\ (\\ begin {array} {r} \(\ c= 200\) |
Agrega lo contrario de la segunda ecuación para eliminar un término y resolver para\(\ c\). | ||||
| \ (\\ begin {array} {r} a+200&=&800\\ -200&&-200\ \ hline a&=&600 \ end {array}\) |
Sustituye 200 in por\(\ c\) en una de las ecuaciones originales. | ||||
|
Verifique su respuesta sustituyendo\(\ a=600\) y\(\ c=200\) en el sistema original. Las respuestas verifican. |
Se vendieron 600 boletos para adultos y 200 boletos infantiles.
Resumen
Combinar ecuaciones es una poderosa herramienta para resolver un sistema de ecuaciones. Sumar o restar dos ecuaciones para eliminar una variable común se denomina método de eliminación (o suma). Una vez que se elimina una variable, se vuelve mucho más fácil de resolver para la otra. La multiplicación se puede utilizar para configurar términos coincidentes en ecuaciones antes de que se combinen. Al usar la multiplicación en el método de eliminación, es importante multiplicar todos los términos en ambos lados de la ecuación, no solo el término que estás tratando de eliminar.


