16.5.1: Raíces Cuadradas y Completar el Cuadrado
- Page ID
- 111290
- Resolver ecuaciones cuadráticas usando la Propiedad Raíz Cuadrada.
- Identificar y completar trinomios cuadrados perfectos.
- Resuelve ecuaciones cuadráticas completando el cuadrado.
Introducción
Las ecuaciones cuadráticas se pueden resolver de muchas maneras. Es posible que ya estés familiarizado con la factorización para resolver algunas ecuaciones cuadráticas. Sin embargo, no todas las ecuaciones cuadráticas pueden ser factorizadas. En este tema, usarás raíces cuadradas para aprender otra forma de resolver ecuaciones cuadráticas, y este método funcionará con todas las ecuaciones cuadráticas.
Resolviendo cuadráticas usando raíces cuadradas
Una forma de resolver la ecuación cuadrática\(\ x^{2}=9\) es restar 9 de ambos lados para obtener un lado igual a 0:\(\ x^{2}-9=0\). La expresión de la izquierda se puede factorizar:
\(\ (x+3)(x-3)=0\)Usando la propiedad de factor cero, sabes que esto significa\(\ x+3=0\) o\(\ x-3=0\), así\(\ x=-3\) o 3.
Otra propiedad te permitiría resolver esa ecuación más fácilmente.
Si\(\ x^{2}=a\), entonces\(\ x=\sqrt{a}\) o\(\ -\sqrt{a}\).
El inmueble anterior dice que se puede tomar la raíz cuadrada de ambos lados de una ecuación, pero hay que pensar en dos casos: la raíz cuadrada positiva de\(\ a\) y la raíz cuadrada negativa de\(\ a\).
Una forma de atajo para escribir\(\ \sqrt{a}\) "" "o\(\ -\sqrt{a}\)" "es"\(\ \pm \sqrt{a}\)”. El símbolo\(\ \pm\) suele leerse “positivo o negativo”. Si se usa como operación (suma o resta), se lee “más o menos”.
Resuelve usando la Propiedad Raíz Cuadrada. \(\ x^{2}=9\)
Solución
| \ (\\ begin {array} {r} x^ {2} =9\\ x=\ pm\ sqrt {9}\\ x=\ pm 3 \ end {array}\) |
Ya que un lado es simple\(\ x^{2}\), puedes tomar la raíz cuadrada de ambos lados para llegar a un\(\ x\) lado. ¡No olvides usar raíces cuadradas tanto positivas como negativas! |
\(\ x=\pm 3\)(es decir,\(\ x=3\) o -3)
Observe que aquí hay una diferencia en resolver\(\ x^{2}=9\) y encontrar\(\ \sqrt{9}\). Para\(\ x^{2}=9\), usted está buscando todos los números cuyo cuadrado es 9. Para\(\ \sqrt{9}\), solo quieres la raíz cuadrada principal (no negativa). El negativo de la raíz cuadrada principal es\(\ -\sqrt{9}\); ambos serían\(\ \pm \sqrt{9}\). A menos que haya un símbolo delante del signo radical, ¡solo se quiere el valor no negativo!
En el ejemplo anterior, puedes tomar la raíz cuadrada de ambos lados fácilmente porque solo hay un término en cada lado. En algunas ecuaciones, es posible que necesites hacer algún trabajo para obtener la ecuación en esta forma. Encontrarás que esto implica aislar\(\ x^{2}\).
Resolver. \(\ 10 x^{2}+5=85\)
Solución
| \(\ 10 x^{2}+5=85\) | Si intentas tomar la raíz cuadrada de ambos lados de la ecuación original, tendrás a\(\ \sqrt{10 x^{2}+5}\) la izquierda, y no puedes simplificar eso. Restar 5 de ambos lados para obtener el\(\ x^{2}\) término por sí mismo. |
| \(\ 10 x^{2}=80\) | Ahora podrías tomar la raíz cuadrada de ambos lados, pero tendrías\(\ \sqrt{10}\) como coeficiente, y necesitarías dividir por ese coeficiente. Dividir por 10 antes de tomar la raíz cuadrada será un poco más fácil. |
| \ (\\ comenzar {alineado} x^ {2} &=8\\ x &=\ pm\ sqrt {8}\\ &=\ pm\ sqrt {(4) (2)}\\ &=\ pm\ sqrt {4}\ sqrt {2}\\ &=\ pm 2\ sqrt {2} \ end {alineado }\) |
Ahora solo tienes a la\(\ x^{2}\) izquierda, por lo que puedes usar la Propiedad Raíz Cuadrada fácilmente. Asegúrese de simplificar lo radical si es posible. |
\(\ x=\pm 2 \sqrt{2}\)
A veces más que solo el\(\ x\) está siendo cuadrado:
Resolver. \(\ (x-2)^{2}-50=0\)
Solución
| \(\ (x-2)^{2}-50=0\) | Nuevamente, tomar la raíz cuadrada de ambos lados en esta etapa dejará algo con lo que no se puede trabajar a la izquierda. Comience agregando 50 a ambos lados. |
| \ (\\ begin {array} {r} (x-2) ^ {2} =50\\ x-2=\ pm\ sqrt {50} \ end {array}\) |
Debido a que\(\ (x-2)^{2}\) es una cantidad cuadrada, se puede tomar la raíz cuadrada de ambos lados. |
| \ (\\ comenzar {alineado} x &=2\ pm\ sqrt {50}\\ &=2\ pm\ sqrt {(25) (2)}\\ &=2\ pm\ sqrt {25}\ sqrt {2}\\ &=2\ pm 5\ sqrt {2} \ end {alineado}\) |
Para aislar\(\ x\) a la izquierda, es necesario agregar 2 a ambos lados. Asegúrese de simplificar lo radical si es posible. |
\(\ x=2 \pm 5 \sqrt{2}\)
Este método puede ser útil a la hora de resolver problemas del mundo real.
La fórmula para componer el interés anual es\(\ A=P(1+r)^{t}\), dónde\(\ A\) está el saldo después de\(\ t\) años, cuándo\(\ P\) es el principal (monto inicial invertido) y\(\ r\) es la tasa de interés.
Encuentra la tasa de interés\(\ r\) si se invierten $3,000 y crece a $3,307.50 después de 2 años.
Solución
| \ (\\ comenzar {alineado} A&=P (1+r) ^ {t}\\ A&=3,307,50\\ t&=2\\ P&=3,000 \ final {alineado}\) |
Primero, identifica lo que sabes. El monto después de 2 años es de 3,307.50, entonces\(\ A=3,307.50\). Esto también significa\(\ t=2\). El principal\(\ P\) es el monto original invertido, por lo que es de 3,000. |
| \(\ 3,307.50=3,000(1+r)^{2}\) | Sustituye los valores por las variables que conozcas. Sólo\(\ r\) queda, así que trata de aislar\(\ r\). |
| \ (\\ comenzar {alineado} \ frac {3,307.50} {3,000} & =( 1+r) ^ {2}\\ 1.1025 & =( 1+r) ^ {2}\\ \ pm\ sqrt {1.1025} &=1+r \ end {alineado}\) |
Dividiendo ambos lados por 3,000 hojas sólo\(\ (1+r)^{2}\) a la derecha. Debido a que\(\ (1+r)^{2}\) es una cantidad cuadrada, puede usar la Propiedad Raíz Cuadrada. |
| \(\ \pm 1.05=1+r\) |
¡No olvides el\(\ \pm\)! Usando una calculadora, puedes encontrar que\(\ \sqrt{1.1025}\) es 1.05. |
| \(\ \pm 1.05-1=r\) | Restar 1 de ambos lados para aislarlo\(\ r\) a la derecha. |
| \ (\\ comenzar {alineado} 1.05-1&=r\ text {o}\\ -1.05-1&=r \ end {alineado}\) |
Ahora tienes dos ecuaciones, una usando 1.05 y otra usando -1.05. |
| \(\ r=0.05 \text { or }-2.05\) | Simplificar las dos ecuaciones da dos soluciones a la ecuación. |
| La tasa de interés es 0.05 o 5% | Observe que una tasa de interés negativa no tiene sentido para este contexto, por lo que solo el valor positivo podría ser la tasa de interés. El -2.05 es una solución extraña y debe desecharse. |
Resolver. \(\ (x-3)^{2}-2=16\)
- \(\ x=3 \pm 3 \sqrt{2}\)
- \(\ x=3+3 \sqrt{2}\)
- \(\ x=7\)
- \(\ x=1 \text { or } 9\)
- Contestar
-
- Correcto. Antes de tomar la raíz cuadrada, agregue 2 a ambos lados:\(\ (x-3)^{2}=18\). Aplicar la Propiedad Raíz Cuadrada da\(\ x-3=\pm \sqrt{18}\), así\(\ x=3 \pm \sqrt{18}\). Simplificando lo radical da\(\ 3 \pm 3 \sqrt{2}\).
- Incorrecto. Olvidaste la raíz cuadrada negativa cuando tomaste la raíz cuadrada de ambos lados. Antes de tomar la raíz cuadrada, agregue 2 a ambos lados:\(\ (x-3)^{2}=18\). Aplicar la Propiedad Raíz Cuadrada da\(\ x-3=\pm \sqrt{18}\), así\(\ x=3 \pm \sqrt{18}\). Simplificando lo radical da\(\ 3 \pm 3 \sqrt{2}\).
- Incorrecto. Aquí hay dos errores: Saber la raíz cuadrada de 16 podría haberte hecho olvidar que para resolver esta ecuación, es necesario aislar la cantidad cuadrada. Antes de tomar la raíz cuadrada, agregue 2 a ambos lados:\(\ (x-3)^{2}=18\). Aplicando la Propiedad Raíz Cuadrada da\(\ x-3=\pm \sqrt{18}\). (Obsérvese que se incluyen tanto las raíces cuadradas positivas como las negativas; este es el otro error probable.) Entonces,\(\ x=3 \pm \sqrt{18}\). Simplificando lo radical da\(\ 3 \pm 3 \sqrt{2}\).
- Incorrecto. Conocer la raíz cuadrada de 16 podría haberte hecho olvidar que para resolver esta ecuación, es necesario aislar la cantidad cuadrada. Antes de tomar la raíz cuadrada, agregue 2 a ambos lados:\(\ (x-3)^{2}=18\). Aplicando la Propiedad Raíz Cuadrada da\(\ x-3=\pm \sqrt{18}\). Entonces,\(\ x=3 \pm \sqrt{18}\). Simplificando lo radical da\(\ 3 \pm 3 \sqrt{2}\).
Trinomios Cuadrados Perfectos
Por supuesto, las ecuaciones cuadráticas a menudo no vendrán en el formato de los ejemplos anteriores. La mayoría de ellos tendrán\(\ x\) términos. Sin embargo, es posible que puedas factorizar la expresión en un binomio cuadrado y, si no, aún puedes usar binomios cuadrados para ayudarte.
Primero, consideremos los binomios al cuadrado. Algunos de los ejemplos anteriores tienen binomios cuadrados:\(\ (1+r)^{2}\) y\(\ (x-2)^{2}\) son binomios cuadrados. (Son binomios, dos términos, que son al cuadrado.) Si expandes estos, obtienes un trinomio cuadrado perfecto. Por ejemplo,\(\ (1+r)^{2}=(1+r)(1+r)=1+2 r+r^{2}\), o\(\ r^{2}+2 r+1\). El trinomio\(\ r^{2}+2 r+1\) es un trinomio cuadrado perfecto. Observe que el primer y último término son cuadrados (\(\ r^{2}\)y 1). El término medio es el doble del producto de las raíces cuadradas del primer y último término, las raíces cuadradas son\(\ r\) y 1, y el término medio es\(\ 2(r)(1)\).
Los trinomios cuadrados perfectos tienen la forma\(\ r^{2}+2 r s+s^{2}\) y se pueden factorizar como\(\ (r+s)^{2}\), o tienen la forma\(\ r^{2}-2 r s+s^{2}\) y se pueden factorizar como\(\ (r-s)^{2}\). Vamos a factorizar un trinomio cuadrado perfecto en un binomio cuadrado.
Factor\(\ 9 x^{2}-24 x+16\).
Solución
| \ (\\ begin {array} {r} 9 x^ {2} =( 3 x) ^ {2}\\ 16=4^ {2} \ end {array}\) |
Primero, observe que el\(\ x^{2}\) término y el término constante son ambos cuadrados perfectos. |
| \(\ 24 x=2(3 x)(4)\) | Entonces note que el término medio (ignorando el signo) es el doble del producto de las raíces cuadradas de los otros términos. |
| \ (\\ begin {array} {r} r=3 x\\ s=4 \ end {array}\) |
Un trinomio en la forma se\(\ r^{2}-2 r s+s^{2}\) puede factorizar como\(\ (r-s)^{2}\). |
| \(\ 9 x^{2}-24 x+16=(3 x-4)^{2}\) | En este caso, se resta el término medio, así restarlo\(\ r\)\(\ s\) y cuadrarlo para obtener\(\ (r-s)^{2}\). |
\(\ (3 x-4)^{2}\)
Puedes usar el procedimiento en este siguiente ejemplo para ayudarte a resolver ecuaciones donde identifiques trinomios cuadrados perfectos, incluso si la ecuación no se establece igual a 0.
Resolver. \(\ 4 x^{2}+20 x+25=8\)
Solución
| \(\ 4 x^{2}+20 x+25=8\) |
Dado que hay un\(\ x\) término, no puede usar la Propiedad Raíz Cuadrada inmediatamente (o incluso después de agregar o dividir por una constante). Observe, sin embargo, que los términos\(\ x^{2}\) y constantes a la izquierda son a la vez cuadrados perfectos:\(\ (2 x)^{2}\) y\(\ 5^{2}\). Consulta el término medio: ¿es así\(\ 2(2 x)(5)\)? ¡Sí! |
| \(\ (2 x+5)^{2}=8\) | Un trinomio en la forma se\(\ r^{2}+2 r s+s^{2}\) puede factorizar como\(\ (r+s)^{2}\), así reescribe el lado izquierdo como un binomio cuadrado. |
| \ (\\ comenzar {alineado} 2 x+5 &=\ pm\ sqrt {8}\\ 2 x &=-5\ pm\ sqrt {8}\\ x &=-\ frac {5} {2}\ pm\ frac {1} {2}\ sqrt {8} \ end {alineado}\) |
Ahora puedes usar la Propiedad Raíz Cuadrada. Se necesitan algunos pasos adicionales para aislar. |
| \ (\\ comenzar {matriz} {l} x=-\ frac {5} {2}\ pm\ frac {1} {2}\ sqrt {4}\ sqrt {2}\ x=-\ frac {5} {2}\ pm\ frac {1} {2} (2)\ sqrt {2}\ x=-\ frac {5} {2}\ pm\ sqrt {2} \ end {array}\) |
Simplifica lo radical cuando sea posible. |
\(\ x=-\frac{5}{2} \pm \sqrt{2}\)
Es posible que hayas mirado el problema de arriba y pensado: “¿Por qué no restar 8 de ambos lados primero, haciendo la ecuación\(\ 4 x^{2}+20 x+17=0\)?” Esta es una técnica para resolver para\(\ x\). El problema es que, aunque hicieras esto, la ecuación\(\ 4 x^{2}+20 x+17=0\) no se puede factorizar con números reales. (Pruébalo. ¿Se te ocurren dos números cuyo producto es 68 y cuya suma es 20?)
Dado que la expresión\(\ 4 x^{2}+20 x+25\) puede identificarse como un trinomio cuadrado perfecto, lo mejor es factorizarla como\(\ (2 x+5)^{2}\) y luego usar la Propiedad Raíz Cuadrada.
Completando la Plaza
Una forma de resolver ecuaciones cuadráticas es completando el cuadrado. Cuando no tienes un trinomio cuadrado perfecto, puedes crear uno agregando un término constante que sea un cuadrado perfecto a ambos lados de la ecuación. Veamos cómo encontrar ese término constante.
“Completar la plaza” hace exactamente lo que dice: toma algo que no es un cuadrado y lo convierte en uno. Esta idea se puede ilustrar utilizando un modelo de área del binomio\(\ x^{2}+b x\).
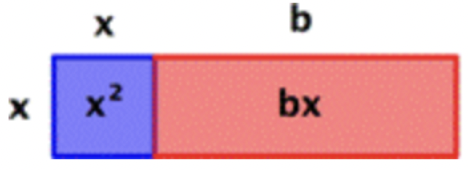\(\ x(x+b)=x^{2}+b x\)
En este ejemplo, el área del rectángulo general viene dada por\(\ x(x+b)\).
Ahora hagamos este rectángulo en un cuadrado. Primero, divida el rectángulo rojo con área\(\ bx\) en dos rectángulos iguales cada uno con área\(\ \frac{b}{2} x\). Después rote y reposicione uno de ellos. No has cambiado el tamaño del área roja; aún así suma\(\ bx\).
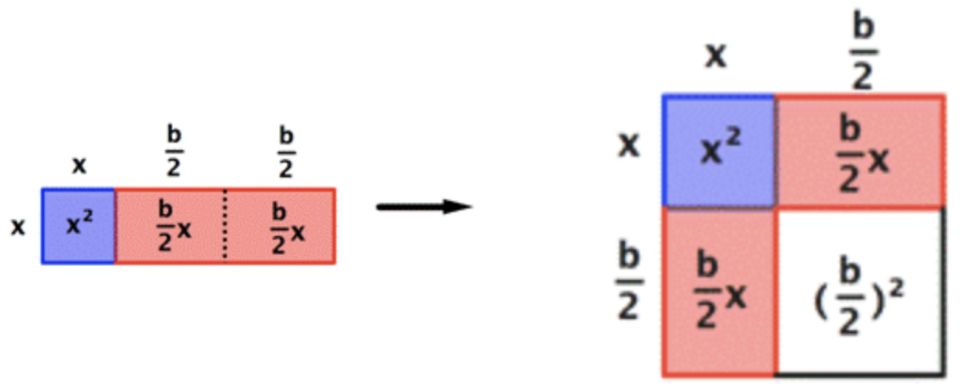\(\ x^{2}+2\left(\frac{b}{2}\right) x+\left(\frac{b}{2}\right)^{2}\)
Los rectángulos rojos ahora conforman dos lados de un cuadrado, que se muestra en blanco. El área de ese cuadrado es la longitud de los rectángulos rojos cuadrados, o\(\ \left(\frac{b}{2}\right)^{2}\).
Aquí viene la parte fría: cuando se agrega el cuadrado blanco a las regiones azul y rojo, toda la forma también es ahora un cuadrado. En otras palabras, ¡has “completado la plaza!” Al agregar la cantidad\(\ \left(\frac{b}{2}\right)^{2}\) al binomio original, has hecho un cuadrado, un cuadrado con lados de\(\ x+\frac{b}{2}\).
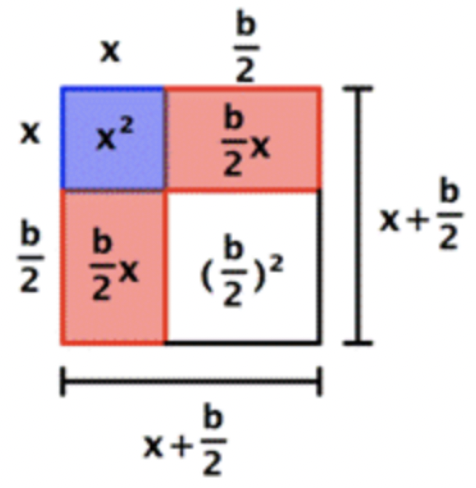\(\ x^{2}+b x+\left(\frac{b}{2}\right)^{2}=x^{2}+2\left(\frac{b}{2}\right) x+\left(\frac{b}{2}\right)^{2}=\left(x+\frac{b}{2}\right)^{2}\)
Observe que el área de este cuadrado puede escribirse como un binomio cuadrado:\(\ \left(x+\frac{b}{2}\right)^{2}\)
Para completar el cuadrado para una expresión de la forma\(\ x^{2}+b x\):
- Identificar el valor de\(\ b\);
- Calcular y agregar\(\ \left(\frac{b}{2}\right)^{2}\).
La expresión se vuelve\(\ x^{2}+b x+\left(\frac{b}{2}\right)^{2}=\left(x+\frac{b}{2}\right)^{2}\).
Encuentra el número a agregar\(\ x^{2}+8 x\) para convertirlo en un trinomio cuadrado perfecto.
Solución
| \ (\\ begin {array} {c} x^ {2} +8 x\\ b=8 \ end {array}\) |
Primero, identificar\(\ b\) si esta tiene la forma\(\ x^{2}+b x\). |
| \(\ x^{2}+8 x+\left(\frac{8}{2}\right)^{2}\) |
Para completar el cuadrado, agregue\(\ \left(\frac{b}{2}\right)^{2}\). \(\ b=8\), entonces\(\ \left(\frac{b}{2}\right)^{2}=\left(\frac{8}{2}\right)^{2}\) Simplificar. |
| \ (\\ begin {array} {r} x^ {2} +8 x+ (4) ^ {2}\\ x^ {2} +8 x+16 \ end {array}\) |
Comprobar que el resultado sea un trinomio cuadrado perfecto. |
| \(\ x^{2}+8 x+16=(x+4)^{2}\) |
\(\ (x+4)^{2}=x^{2}+4 x+4 x+16=x^{2}+8 x+16\) ¡Lo es! |
Agregar\(\ +16\) hará\(\ x^{2}+8 x\) un trinomio cuadrado perfecto.
Observe que siempre\(\ \left(\frac{b}{2}\right)^{2}\) es positivo, ya que es el cuadrado de un número. Cuando completas el cuadrado, siempre estás agregando un valor positivo.
Usa completar el cuadrado para encontrar el valor a agregar que hace\(\ x^{2}-12 x\) un trinomio cuadrado perfecto. Después escribe la expresión como el cuadrado de un binomio.
- Agregar 12. \(\ (x-6)^{2}\)
- Agregar 36. \(\ (x+6)^{2}\)
- Agregar -12. \(\ (x-12)^{2}\)
- Agregar 36. \(\ (x-6)^{2}\)
- Contestar
-
- Incorrecto. El valor de\(\ b\) es -12, por lo que el valor a sumar es\(\ \left(\frac{-12}{2}\right)^{2}=(-6)^{2}=36\), no 12. Agrega 36 para obtener\(\ x^{2}-12 x+36\). La respuesta correcta es\(\ (x-6)^{2}\).
- Incorrecto. El valor a sumar se ha calculado correctamente:\(\ \left(\frac{-12}{2}\right)^{2}=(-6)^{2}=36\). Sin embargo, el trinomio resultante es\(\ x^{2}-12 x+36\), que factores a\(\ (x-6)^{2}\), no\(\ (x+6)^{2}\). La respuesta correcta es\(\ (x-6)^{2}\).
- Incorrecto. El valor de\(\ b\) es -12, por lo que el valor a sumar es\(\ \left(\frac{-12}{2}\right)^{2}=(-6)^{2}=36\), no -12. Tenga en cuenta también, que el número que agregue siempre será positivo porque es el cuadrado de un número. La respuesta correcta es\(\ (x-6)^{2}\).
- Correcto. El valor a agregar es\(\ \left(\frac{-12}{2}\right)^{2}=(-6)^{2}=36\) y los\(\ x^{2}-12 x+36\) factores trinomiales resultantes para:\(\ (x-6)^{2}\)
Resolver una ecuación cuadrática usando Completar el Cuadrado
Puedes usar completar el cuadrado para ayudarte a resolver una ecuación cuadrática que no se puede resolver factorizando.
Empecemos por ver qué sucede cuando completas el cuadrado en una ecuación. En el siguiente ejemplo, observe que completar el cuadrado resultará en agregar un número a ambos lados de la ecuación. ¡Tienes que hacer esto para mantener a ambos lados iguales!
Reescribe\(\ x^{2}+6 x=8\) para que el lado izquierdo sea un trinomio cuadrado perfecto.
Solución
| \ (\\ begin {array} {r} x^ {2} +6 x=8\\ b=6 \ end {array}\) |
Esta ecuación tiene una constante de 8. Ignorarlo por ahora y enfocarse en los\(\ x\) términos\(\ x^{2}\) y en el lado izquierdo de la ecuación. El lado izquierdo tiene la forma\(\ x^{2}+b x\), por lo que puedes identificar\(\ b\). Para completar el cuadrado, agréguese\(\ \left(\frac{b}{2}\right)^{2}\) al lado izquierdo. |
| \(\ x^{2}+6 x+9=8+9\) |
\(\ b=6, \text { so }\left(\frac{b}{2}\right)^{2}=\left(\frac{6}{2}\right)^{2}=3^{2}=9\) Sin embargo, esta es una ecuación, por lo que también debes agregar el mismo número al lado derecho. |
| Simplificar. | |
| \(\ x^{2}+6 x+9=17\) | Comprobar que el lado izquierdo es un trinomio cuadrado perfecto. |
| \ (\\ begin {array} {r} x^ {2} +6 x+9=17\\ (x+3) ^ {2} =17 \ end {array}\) |
\(\ (x+3)^{2}=x^{2}+3 x+3 x+9=x^{2}+6 x+9\) ¡Lo es! |
\(\ x^{2}+6 x+9=17\)
¿Ves que completar el cuadrado en una ecuación es muy similar a completar el cuadrado en una expresión? La principal diferencia es que hay que sumar el nuevo número (+9 en este caso) a ambos lados de la ecuación para mantener la igualdad.
Ahora veamos un ejemplo donde estás usando completar el cuadrado para resolver realmente una ecuación, encontrando un valor para la variable.
Resolver. \(\ x^{2}-12 x-4=0\)
Solución
| \ (\\ begin {array} {r} x^ {2} -12 x=4\\ b=-12 \ end {array}\) |
Ya que no se puede factorizar el trinomio en el lado izquierdo, utilizará completar el cuadrado para resolver la ecuación. Reescribe la ecuación con el lado izquierdo en el formulario\(\ x^{2}+b x\), para prepararte para completar el cuadrado. Identificar\(\ b\). |
| \ (\\ begin {array} {r} x^ {2} -12 x+36=4+36\ x^ {2} -12 x+36=40 \ end {array}\) |
Averigua qué valor agregar para completar el cuadrado. Agrega\(\ \left(\frac{b}{2}\right)^{2}\) para completar el cuadrado, así:\(\ \left(\frac{b}{2}\right)^{2}=\left(\frac{-12}{2}\right)^{2}=(-6)^{2}=36\) Agregue el valor a ambos lados de la ecuación y simplifique. |
| \(\ (x-6)^{2}=40\) | Reescribe el lado izquierdo como un binomio cuadrado. |
| \(\ x-6=\pm \sqrt{40}\) | Utilice la Propiedad Raíz Cuadrada. Recuerda incluir tanto la raíz cuadrada positiva como la negativa, o te perderás una de las soluciones. |
| \ (\\ comenzar {alineado} x &=6\ pm\ sqrt {40}\\ &=6\ pm\ sqrt {4}\ sqrt {10}\\ &=6\ pm 2\ sqrt {10} \ end {alineado}\) |
Resuelve\(\ x\) agregando 6 a ambos lados. Simplifique según sea necesario. |
\(\ x=6 \pm 2 \sqrt{10}\)
Te habrás dado cuenta de que debido a que tienes que usar ambas raíces cuadradas, todos los ejemplos tienen dos soluciones. Aquí hay otro ejemplo que es ligeramente diferente.
Resolver. \(\ x^{2}+16 x+17=-47\)
Solución
| \ (\\ begin {array} {r} x^ {2} +16 x=-64\\ b=16 \ end {array}\) |
Reescribe la ecuación para que el lado izquierdo tenga la forma\(\ x^{2}+b x\). Identificar\(\ b\). |
| \ (\\ begin {array} {r} x^ {2} +16 x+64=-64+64\\ x^ {2} +16 x+64=0 \ end {array}\) |
Agregar\(\ \left(\frac{b}{2}\right)^{2}\), es decir\(\ \left(\frac{16}{2}\right)^{2}=8^{2}=64\), a ambos lados. |
| \(\ (x+8)^{2}=0\) | Escribe el lado izquierdo como un binomio cuadrado. |
| \(\ x+8=0\) | Toma las raíces cuadradas de ambos lados. Normalmente se necesitan raíces cuadradas tanto positivas como negativas, pero 0 no es ni positivo ni negativo. 0 tiene sólo una raíz. |
| \(\ x=-8\) | Resolver para\(\ x\). |
\(\ x=-8\)
Echa un vistazo más de cerca a este problema y es posible que veas algo familiar. En lugar de completar el cuadrado, intenta sumar 47 a ambos lados en la ecuación. La ecuación\(\ x^{2}+16 x+17=-47\) se convierte\(\ x^{2}+16 x+64=0\). ¿Se puede factorizar esta ecuación usando agrupación? (Piense en dos números cuyo producto es 64 y cuya suma es 16).
Se puede factorizar como\(\ (x+8)(x+8)=0\), por supuesto! Saber completar el cuadrado es muy útil, pero no siempre es la única manera de resolver una ecuación.
Resolver. \(\ x^{2}-16 x=-1\)
- \(\ x=4 \pm \sqrt{15}\)
- \(\ x=-8 \pm 3 \sqrt{7}\)
- \(\ x=8 \pm i\)
- \(\ x=8 \pm 3 \sqrt{7}\)
- Contestar
-
- Incorrecto. Parece que has agregado 16 y luego factorizado el trinomio incorrectamente. No obstante, el valor de\(\ b\) es -16, por lo que para completar el cuadrado, sumar\(\ \left(\frac{-16}{2}\right)^{2}=(-8)^{2}=64\) (no 16). Agrega 64 a ambos lados para obtener\(\ x^{2}-16 x+64=63\). Esto es\(\ (x-8)^{2}=63\), entonces\(\ x-8=\pm \sqrt{63}\). Eso quiere decir\(\ x=8 \pm \sqrt{63}=8 \pm 3 \sqrt{7}\). La respuesta correcta es\(\ x=8 \pm 3 \sqrt{7}\).
- Incorrecto. El valor a sumar se ha calculado correctamente:\(\ \left(\frac{-8}{2}\right)^{2}=(-8)^{2}=64\). Sin embargo, el trinomio resultante es\(\ x^{2}-16 x+64\), que factores a\(\ (x-8)^{2}\), no\(\ (x+8)^{2}\). La ecuación se vuelve\(\ (x-8)^{2}=63\), así\(\ x-8=\pm \sqrt{63}\), lo que significa que\(\ x=8 \pm \sqrt{63}=8 \pm 3 \sqrt{7}\). La respuesta correcta es\(\ x=8 \pm 3 \sqrt{7}\).
- Incorrecto. El valor a sumar se ha calculado correctamente:\(\ \left(\frac{-8}{2}\right)^{2}=(-8)^{2}=64\). No obstante, parece haber agregado 64 solo al lado izquierdo de la ecuación, y no al lado derecho. La ecuación se vuelve\(\ (x-8)^{2}=63\), así\(\ x-8=\pm \sqrt{63}\), lo que significa que\(\ x=8 \pm \sqrt{63}=8 \pm 3 \sqrt{7}\). La respuesta correcta es\(\ x=8 \pm 3 \sqrt{7}\).
- Correcto. El valor de\(\ b\) es -16, por lo que para completar el cuadrado, agregue\(\ \left(\frac{-16}{2}\right)^{2}=(-8)^{2}=64\). Agrega 64 a ambos lados para obtener\(\ x^{2}-16 x+64=63\). Esto es\(\ (x-8)^{2}=63\), entonces\(\ x-8=\pm \sqrt{63}\). Eso quiere decir\(\ x=8 \pm \sqrt{63}=8 \pm 3 \sqrt{7}\).
Resumen
Completar el cuadrado se utiliza para cambiar un binomio de la forma\(\ x^{2}+b x\) en un trinomio cuadrado perfecto\(\ x^{2}+b x+\left(\frac{b}{2}\right)^{2}\), que se puede factorizar a\(\ \left(x+\frac{b}{2}\right)^{2}\). Al resolver ecuaciones cuadráticas completando el cuadrado, tenga cuidado de agregar\(\ \left(\frac{b}{2}\right)^{2}\) a ambos lados de la ecuación para mantener la igualdad. La propiedad de raíz cuadrada se puede usar para resolver\(\ x\). Con la Propiedad Raíz Cuadrada, tenga cuidado de incluir tanto la raíz cuadrada principal como su opuesta. Asegúrese de simplificar según sea necesario.