16.5.2: La fórmula cuadrática

Última actualización
Guardar como PDF

Page ID: 111291

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Escriba una ecuación cuadrática en forma estándar e identifique los valores de$\ a$$\ b$, y$\ c$ en una ecuación cuadrática de forma estándar.
Usa la Fórmula Cuadrática para encontrar todas las soluciones reales.
Utilice la Fórmula Cuadrática para encontrar todas las soluciones complejas.
Calcular el discriminante e indicar el número y tipo de soluciones.
Resolver problemas de aplicación que requieran el uso de la Fórmula Cuadrática.

Introducción

Puedes resolver cualquier ecuación cuadrática completando el cuadrado, o reescribiendo parte de la ecuación como un trinomio cuadrado perfecto. Si completas el cuadrado en la ecuación genérica$\ a x^{2}+b x+c=0$ y luego resuelves por$\ x$, lo encuentras$\ x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$. Esta ecuación se conoce como la Fórmula Cuadrática.

Esta fórmula es muy útil para resolver ecuaciones cuadráticas que son difíciles o imposibles de factorizar, y su uso puede ser más rápido que completar el cuadrado. La Fórmula Cuadrática se puede utilizar para resolver cualquier ecuación cuadrática de la forma$\ a x^{2}+b x+c=0$.

Forma estándar

La forma$\ a x^{2}+b x+c=0$ se llama la forma estándar de una ecuación cuadrática. Antes de resolver una ecuación cuadrática usando la Fórmula Cuadrática, es vital que estés seguro de que la ecuación está en esta forma. Si no lo haces, podrías usar los valores incorrectos para$\ a$,$\ b$, y$\ c$, y luego la fórmula dará soluciones incorrectas.

Ejemplo

Reescribir la ecuación$\ 3 x+2 x^{2}+4=5$ en forma estándar e identificar$\ a$,$\ b$, y$\ c$.

Solución

\ (\\ begin {array} {l}
3 x+2 x^ {2} +4=5\\
3 x+2 x^ {2} +4-5=5-5
\ end {array}\)

Primero, asegúrate de que el lado derecho de la ecuación sea 0. En este caso, todo lo que necesitas hacer es restar 5 de ambos lados.

\ (\\ begin {array} {l}
3 x+2 x^ {2} -1=0\\
2 x^ {2} +3 x-1=0
\ end {array}\)

Simplifica, y escribe los términos con el exponente en la variable en orden descendente.

\ (\\ begin {array} {lll}
2 x^ {2}\ quad + & 3 x\ quad- & 1 & =0\\\ flecha abajo &
\ flecha abajo &\ flecha abajo &\ flecha abajo\\
a x^ {2} & b x & c
\ end {array}\)

$\ a=2, b=3, c=-1$

Ahora que la ecuación está en forma estándar, se pueden leer los valores de$\ a$,$\ b$, y$\ c$ a partir de los coeficientes y constante. Tenga en cuenta que dado que la constante 1 se resta,$\ c$ debe ser negativa.

$\ 2 x^{2}+3 x-1=0 ; a=2, b=3, c=-1$

Ejemplo

Reescribir la ecuación$\ 2(x+3)^{2}-5 x=6$ en forma estándar e identificar$\ a$,$\ b$, y$\ c$.

Solución

\ (\\ begin {array} {l}
2 (x+3) ^ {2} -5 x=6\\
2 (x+3) ^ {2} -5 x-6=6-6
\ end {array}\)

Primero, asegúrate de que el lado derecho de la ecuación sea 0.

\ (\\ begin {array} {l}
2\ left (x^ {2} +6 x+9\ derecha) -5 x-6=0\\
2 x^ {2} +12 x+18-5 x-6=0\\
2 x^ {2} +12 x-5 x+18-6=0\\
2 x^ {2} +7 x+12=0
\ end {array}\)

\ (\\ begin {array} {lll}
2 x^ {2}\ quad+ & 7 x\ quad+ & 12=0\\
\ flecha abajo &\ flecha abajo &\ flecha abajo\\ flecha abajo\\
a & b & c
\ end {array}\)

$\ a=2, b=7, c=12$

Expande el binomio al cuadrado, luego simplifica combinando términos similares.

Asegúrese de escribir los términos con el exponente en la variable en orden descendente.

Ahora que la ecuación está en forma estándar, se pueden leer los valores de$\ a$,$\ b$, y$\ c$ a partir de los coeficientes y constante.

$\ 2 x^{2}+7 x+12=0 ; a=2, b=7, c=12$

Ejercicio

Identificar los valores de$\ a$$\ b$,, y$\ c$ en la forma estándar de la ecuación$\ 3 x+x^{2}=6$.

$\ a=3, b=1, c=6$
$\ a=1, b=3, c=6$
$\ a=1, b=3, c=-6$
$\ a=3, b=1, c=-6$

Contestar

Incorrecto. Recuerda que en forma estándar, la ecuación está escrita en la forma$\ a x^{2}+b x+c=0$. $\ 3 x+x^{2}=6$se convierte$\ 3 x+x^{2}-6=0$, por lo que la forma estándar es$\ x^{2}+3 x-6=0$. Esto significa que la respuesta correcta es$\ a=1$,$\ b=3$, y$\ c=-6$.
Incorrecto. Pones los términos en el orden correcto, pero el lado derecho debe ser igual a 0. El$\ c$ debe estar en el lado izquierdo de la ecuación. $\ 3 x+x^{2}=6$se convierte$\ 3 x+x^{2}-6=0$, por lo que la forma estándar es$\ x^{2}+3 x-6=0$. Esto significa que la respuesta correcta es$\ a=1$,$\ b=3$, y$\ c=-6$.
Correcto. $\ 3 x+x^{2}=6$se convierte$\ 3 x+x^{2}-6=0$, por lo que la forma estándar es$\ x^{2}+3 x-6=0$. Esto significa$\ a=1$,$\ b=3$, y$\ c=-6$.
Incorrecto. Recuerda que en forma estándar, la ecuación está escrita en la forma$\ a x^{2}+b x+c=0$. Encontraste correctamente que$\ 3 x+x^{2}=6$ se convierte$\ 3 x+x^{2}-6=0$. Poner los términos en orden da la forma estándar$\ x^{2}+3 x-6=0$. Esto significa que la respuesta correcta es$\ a=1$,$\ b=3$, y$\ c=-6$.

Derivando la Fórmula Cuadrática

Completemos el cuadrado sobre la ecuación general y veamos exactamente cómo eso produce la Fórmula Cuadrática. Recordemos el proceso de completar la plaza.

Comience con una ecuación de la forma$\ x^{2}+b x+c=0$.
Reescribe la ecuación para que$\ x^{2}+b x$ quede aislada en un lado.
Completa el cuadrado agregando$\ \left(\frac{b}{x}\right)^{2}$ a ambos lados.
Reescribir el trinomio cuadrado perfecto como un cuadrado de un binomio.
Utilice la Propiedad Raíz Cuadrada y resuelva para$\ x$.

¿Se puede completar el cuadrado en la ecuación cuadrática general$\ a x^{2}+b x+c=0$? Pruébalo tú mismo antes de continuar con el ejemplo a continuación. Pista: Observe que en la ecuación general, el coeficiente de no$\ x^{2}$ es igual a 1. Puedes dividir la ecuación por$\ a$, lo que hace que algunas de las expresiones sean un poco desordenadas, pero si tienes cuidado, todo saldrá bien, ¡y al final, tendrás la Fórmula Cuadrática!

Ejemplo

Completa la plaza de$\ a x^{2}+b x+c=0$ para llegar a la Fórmula Cuadrática.

Solución

$\ x^{2}+\frac{b}{a} x+\frac{c}{a}=0$	Divide ambos lados de la ecuación por$\ a$, de modo que el coeficiente de$\ x^{2}$ sea 1.
$\ x^{2}+\frac{b}{a} x=-\frac{c}{a}$	Reescribe para que el lado izquierdo esté en la forma$\ x^{2}+b x$, (aunque en este caso$\ bx$ es en realidad$\ \frac{b}{a} x$).
$\ x^{2}+\frac{b}{a} x+\left(\frac{b}{2 a}\right)^{2}=-\frac{c}{a}+\left(\frac{b}{2 a}\right)^{2}$	El coeficiente on$\ x$ es$\ \frac{b}{a}$, por lo que el valor a sumar a ambos lados es$\ \left(\frac{b}{2 a}\right)^{2}$.
$\ \left(x+\frac{b}{2 a}\right)^{2}=-\frac{c}{a}+\left(\frac{b}{2 a}\right)^{2}$	Escribe el lado izquierdo como un binomio cuadrado.
$\ \left(x+\frac{b}{2 a}\right)^{2}=-\frac{c}{a}+\frac{b^{2}}{4 a^{2}}$	Evaluar$\ \left(\frac{b}{2 a}\right)^{2}$ como$\ \frac{b^{2}}{4 a^{2}}$.
$\ \left(x+\frac{b}{2 a}\right)^{2}=-\frac{4 a c}{4 a^{2}}+\frac{b^{2}}{4 a^{2}}$	Escribe las fracciones del lado derecho usando un denominador común.
$\ \left(x+\frac{b}{2 a}\right)^{2}=\frac{b^{2}-4 a c}{4 a^{2}}$	Agrega las fracciones a la derecha.
$\ x+\frac{b}{2 a}=\pm \sqrt{\frac{b^{2}-4 a c}{4 a^{2}}}$	Utilice la Propiedad Raíz Cuadrada. ¡Recuerda que quieres tanto las raíces cuadradas positivas como las negativas!
$\ x=-\frac{b}{2 a} \pm \sqrt{\frac{b^{2}-4 a c}{4 a^{2}}}$	Restar$\ \frac{b}{2 a}$ de ambos lados para aislar$\ x$.
$\ x=-\frac{b}{2 a} \pm \frac{\sqrt{b^{2}-4 a c}}{2 a}$	El denominador bajo el radical es un cuadrado perfecto, entonces:$\ \sqrt{\frac{b^{2}-4 a c}{4 a^{2}}}=\frac{\sqrt{b^{2}-4 a c}}{\sqrt{4 a^{2}}}=\frac{\sqrt{b^{2}-4 a c}}{2 a}$
$\ x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$	Sumar las fracciones ya que tienen un denominador común.

Ahí la tienes, la Fórmula Cuadrática.

Resolver una ecuación cuadrática usando la fórmula cuadrática

La Fórmula Cuadrática funcionará con cualquier ecuación cuadrática, pero sólo si la ecuación está en forma estándar,$\ a x^{2}+b x+c=0$. Para usarlo, sigue estos pasos.

Poner primero la ecuación en forma estándar.
Identificar los coeficientes,$\ a$,$\ b$, y$\ c$. Tenga cuidado de incluir signos negativos si se restan los$\ c$ términos$\ bx$ o.
Sustituir los valores de los coeficientes en la Fórmula Cuadrática.
Simplifica lo más posible.
Usa el$\ \pm$ frente del radical para separar la solución en dos valores: uno en el que se agrega la raíz cuadrada, y otro en el que se resta.
Simplifica ambos valores para obtener las soluciones posibles.

Eso son muchos pasos. Intentemos usar la Fórmula Cuadrática para resolver primero una ecuación relativamente simple; luego volverás y la resolverás de nuevo usando otro método de factorización.

Ejemplo

Usa la Fórmula Cuadrática para resolver la ecuación$\ x^{2}+4 x=5$.

Solución

\ (\\ begin {array} {r} x^ {2} +4 x=5\ x^ {2} +4 x-5=0 \ end {array}\)	Primero, escribe la ecuación en forma estándar. $\ a=1, b=4, c=-5$
\ (\\ begin {array} {l} x^ {2}\ quad+&4 x\ quad-&5=0\\ \ flecha abajo&\ flecha abajo&\ flecha abajo\\ a x^ {2}\ quad+&b x\ quad+&c=0 \ end {array}\) \ (\\ begin {array} {r} x=\ frac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\ x=\ frac {-4\ pm\ sqrt {(4) ^ {2} -4 (1) (-5)}} {2 (1)} \ end {array}\)	Tenga en cuenta que el signo de resta significa que la constante$\ c$ es negativa. Sustituir los valores en la Fórmula Cuadrática.
$\ x=\frac{-4 \pm \sqrt{16+20}}{2}$	Simplificar, teniendo cuidado de que las señales sean correctas.
$\ x=\frac{-4 \pm \sqrt{36}}{2}$	Simplifica un poco más.
$\ x=\frac{-4 \pm 6}{2}$	Simplificar lo radical:$\ \sqrt{36}=6$.
\ (\\ begin {array} {r} x=\ frac {-4+6} {2} =\ frac {2} {2} =1\\ \ texto {o}\\ x=\ frac {-4-6} {2} =\ frac {-10} {2} =-5 \ end {array}\)	Separar y simplificar para encontrar las soluciones a la ecuación cuadrática. Obsérvese que en uno, se suma 6 y en el otro, se resta 6.

$\ x=1 \text { or }-5$

Puede verificar estas soluciones sustituyendo 1 y -5 en la ecuación original. La tabla superior muestra 1 siendo sustituido en la ecuación original, y la tabla inferior muestra -5 siendo sustituido en la ecuación original.

$\ x=1$

$\ x^{2}+4 x=5$

$\ (1)^{2}+4(1)=5$

$\ 1+4=5$

$\ 5=5$

$\ x=-5$

$\ x^{2}+4 x=5$

$\ (-5)^{2}+4(-5)=5$

$\ 25-20=5$

$\ 5=5$

Obtienes dos afirmaciones verdaderas, así sabes que ambas soluciones funcionan:$\ x=1$ o$\ -5$. ¡Has resuelto la ecuación exitosamente usando la Fórmula Cuadrática!

Sin embargo, al mirar$\ x^{2}+4 x=5$, puede que hayas pensado, “ya sé cómo hacer esto; puedo reescribir esta ecuación como$\ x^{2}+4 x-5=0$, y luego factorizarla como$\ (x+5)(x-1)=0$, así$\ x=-5$ o 1”. Esto es correcto, ¡y enhorabuena si hiciste esta conexión!

En ocasiones, puede ser más fácil resolver una ecuación usando métodos convencionales de factorización, como encontrar pares numéricos que sumen a un número (en este ejemplo, 4) y que produzcan un producto específico (en este ejemplo -5) cuando se multiplican. El poder de la Fórmula Cuadrática es que puede ser utilizada para resolver cualquier ecuación cuadrática, incluso aquellas donde encontrar combinaciones numéricas no funcionará.

La mayoría de las ecuaciones cuadráticas que has mirado tienen dos soluciones, como la anterior. El siguiente ejemplo es un poco diferente.

Ejemplo

Usa la Fórmula Cuadrática para resolver la ecuación$\ x^{2}-2 x=6 x-16$.

Solución

\ (\\ begin {array} {r} x^ {2} -2 x=6 x-16\\ x^ {2} -2 x-6 x+16=0\\ x^ {2} -8 x+16=0 \ end {array}\)	Restar$\ 6x$ de cada lado y sumar 16 a ambos lados para poner la ecuación en forma estándar.
\ (\\ begin {array} {l} x^ {2}\ quad-&8 x\ quad+&16=0\\ \ flecha abajo&\ flecha abajo&\ flecha abajo\\ a x^ {2}\ quad+&b x\ quad+&c=0 \ end {array}\)	Identificar los coeficientes$\ a$,$\ b$, y$\ c$. $\ x^{2}=1 x^{2}$, entonces$\ a=1$. Ya que$\ 8x$ se resta,$\ b$ es negativo. $\ a=1, b=-8, c=16$
\ (\\ begin {array} {c} x=\ frac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\ x=\ frac {- (-8)\ pm\ sqrt {(-8) ^ {2} -4 (1) (16)}} {2 (1)} \ end {array}\)	Sustituir los valores en la Fórmula Cuadrática.
$\ x=\frac{8 \pm \sqrt{64-64}}{2}$	Simplificar.
$\ x=\frac{8 \pm \sqrt{0}}{2}=\frac{8}{2}=4$	Dado que la raíz cuadrada de 0 es 0, y tanto sumar como restar 0 dan el mismo resultado, solo hay un valor posible.

$\ x=4$

Nuevamente, verifique usando la ecuación original.

\ (\\ begin {alineado}
x^ {2} -2 x &=6 x-16\\
(4) ^ {2} -2 (4) &=6 (4) -16\\
16-8 &=24-16\\
8 &=8
\ end {alineado}\)

Probemos un último ejemplo. Este también tiene una diferencia en la solución.

Ejemplo

Usa la Fórmula Cuadrática para resolver la ecuación$\ x^{2}+2 x=-5$.

Solución

\ (\\ begin {array} {r} x^ {2} +2 x=-5\ x^ {2} +2 x+5 = 0 \ end {array}\)	Primero, escribe la ecuación en forma estándar.
\ (\\ begin {array} {l} x^ {2}\ quad+&2 x\ quad+&5=0\\ \ flecha abajo&\ flecha abajo&\ flecha abajo\\ a x^ {2}\ quad+&b x\ quad+&\ c=0 \ end {array}\)	$\ a=1, b=2, c=5$
\ (\\ begin {array} {r} x=\ frac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\ x=\ frac {-2\ pm\ sqrt {(2) ^ {2} -4 (1) (5)}} {2 (1)} \ end {array}\)	Sustituir los valores en la Fórmula Cuadrática.
$\ x=\frac{-2 \pm \sqrt{4-20}}{2}$	Simplificar, teniendo cuidado de que las señales sean correctas.
$\ x=\frac{-2 \pm \sqrt{-16}}{2}$	Simplifica un poco más.
$\ x=\frac{-2 \pm 4 i}{2}$	Simplifica el radical, ¡pero fíjate que el número bajo el símbolo radical es negativo! La raíz cuadrada de -16 es imaginaria. $\ \sqrt{-16}=4 i$
\ (\\ begin {array} {r} x=\ frac {-2+4 i} {2} =\ frac {-1+2 i} {1}\ cdot\ frac {2} {2} =-1+2 i\ \ texto {o}\\ x=\ frac {-2-4 i} {2} =\ frac {-1-2 i} {1}\ cdot\ frac {2}} {2} =-1-2 i \ end {array}\)	Separar y simplificar para encontrar las soluciones a la ecuación cuadrática.

$\ x=-1+2 i \text { or }-1-2 i$

Consulta estas soluciones en la ecuación original en las tablas a continuación. Tenga cuidado al expandir los cuadrados y reemplazar$\ i^{2}$ con -1.

\ (\\ begin {array} {c}
x=-1+2 i\\
x^ {2} +2 x=-5\\
(-1+2 i) ^ {2} +2 (-1+2 i) =-5\
1-4 i+4 i^ {2} -2+4 i=-5\\
1-4 i+4 (-1) -2+4 i=-5\
1-4-2=-5\
-5=-5
\ end {array}\)

\ (\\ begin {array} {c}
x=-1-2 i\\
x^ {2} +2 x=-5\\
(-1-2 i) ^ {2} +2 (-1-2 i) =-5\\
1+4 i+4 i^ {2} -2-4 i=-5\\
1+4 i+4 (-1) -2-4 i=-5\\
1-4-2=-5\\
-5=-5
\ end {array}\)

Ejercicio

Usa la Fórmula Cuadrática para resolver la ecuación$\ x^{2}-2 x-4=0$.

$\ x=2$
$\ x=11, x=-9$
$\ x=2+\sqrt{5}, x=2-\sqrt{5}$
$\ x=1+\sqrt{5}, x=1-\sqrt{5}$

Contestar

Incorrecto. Es posible que haya factorizado incorrectamente el lado izquierdo como$\ (x-2)^{2}$. Ya que$\ a=1$,$\ b=-2$, y$\ c=-4$,$\ x=\frac{-(-2) \pm \sqrt{(-2)^{2}-4(1)(-4)}}{2(1)}=\frac{2 \pm \sqrt{4+16}}{2}=\frac{2 \pm \sqrt{20}}{2}=\frac{2 \pm 2 \sqrt{5}}{2}=\frac{2}{2} \pm \frac{2 \sqrt{5}}{2}=1 \pm \sqrt{5}$. La respuesta correcta es$\ x=1+\sqrt{5}$ o$\ x=1-\sqrt{5}$.
Incorrecto. $\ x=\frac{-(-2) \pm \sqrt{(-2)^{2}-4(1)(-4)}}{2(1)}=\frac{2 \pm \sqrt{4+16}}{2}=\frac{2 \pm \sqrt{20}}{2}$. Si ignoras la raíz cuadrada, esto se convierte en$\ x=11$ o$\ x=-9$, así es posible que hayas olvidado tomar la raíz cuadrada de 20. $\ x=\frac{2 \pm \sqrt{20}}{2}=\frac{2 \pm 2 \sqrt{5}}{2}=\frac{2}{2} \pm \frac{2 \sqrt{5}}{2}=1 \pm \sqrt{5}$, lo que significa que la respuesta correcta es$\ x=1+\sqrt{5}$ o$\ x=1-\sqrt{5}$.
Incorrecto. Usando la fórmula,$\ x=\frac{-(-2) \pm \sqrt{(-2)^{2}-4(1)(-4)}}{2(1)}=\frac{2 \pm \sqrt{4+16}}{2}=\frac{2 \pm \sqrt{20}}{2}=\frac{2 \pm 2 \sqrt{5}}{2}$. Si olvidas que el denominador está bajo ambos términos en el numerador, podrías obtener$\ x=2+\sqrt{5}$ o$\ x=2-\sqrt{5}$. No obstante, la simplificación correcta es$\ x=\frac{2 \pm 2 \sqrt{5}}{2}=\frac{2}{2} \pm \frac{2 \sqrt{5}}{2}=1 \pm \sqrt{5}$, por lo que la respuesta es$\ x=1+\sqrt{5}$ o$\ x=1-\sqrt{5}$.
Correcto. Usando la fórmula,$\ x=\frac{-(-2) \pm \sqrt{(-2)^{2}-4(1)(-4)}}{2(1)}=\frac{2 \pm \sqrt{4+16}}{2}=\frac{2 \pm \sqrt{20}}{2}=\frac{2 \pm 2 \sqrt{5}}{2}=\frac{2}{2} \pm \frac{2 \sqrt{5}}{2}=1 \pm \sqrt{5}$, así$\ x=1+\sqrt{5}$ o$\ x=1-\sqrt{5}$.

El discriminante

Estos ejemplos han demostrado que una ecuación cuadrática puede tener dos soluciones reales, una solución real o dos soluciones complejas.

En la Fórmula Cuadrática, la expresión debajo del símbolo radical determina el número y tipo de soluciones que revelará la fórmula. Esta expresión,$\ b^{2}-4 a c$, se llama el discriminante de la ecuación$\ a x^{2}+b x+c=0$.

Pensemos en cómo el discriminante afecta la evaluación de$\ \sqrt{b^{2}-4 a c}$, y cómo ayuda a determinar el conjunto de soluciones.

Si$\ b^{2}-4 a c>0$, entonces el número debajo del radical será un valor positivo. Siempre se puede encontrar la raíz cuadrada de un positivo, por lo que evaluar la Fórmula Cuadrática dará como resultado dos soluciones reales (una sumando la raíz cuadrada positiva y otra restándola).
Si$\ b^{2}-4 a c=0$, entonces estarás tomando la raíz cuadrada de 0, que es 0. Dado que sumar y restar 0 dan ambos el mismo resultado, la$\ \pm$ porción de la fórmula no importa. Habrá una solución real.
Si$\ b^{2}-4 a c<0$, entonces el número debajo del radical será un valor negativo. Como no se puede encontrar la raíz cuadrada de un número negativo usando números reales, no hay soluciones reales. Sin embargo, puedes usar números imaginarios. Entonces tendrás dos soluciones complejas, una sumando la raíz cuadrada imaginaria y otra restándola.

Ejemplo

Utilizar el discriminante para determinar cuántas y qué tipo de soluciones$\ x^{2}-4 x+10=0$ tiene la ecuación cuadrática.

Solución

\ (\\ begin {array} {r} b^ {2} -4 a c\\ (-4) ^ {2} -4 (1) (10) \ end {array}\)	Evaluar$\ b^{2}-4 a c$. Primero tenga en cuenta que$\ a=1$$\ b=-4$,, y$\ c=10$.
$\ 16-40=-24$	El resultado es un número negativo. El discriminante es negativo, por lo que la ecuación cuadrática tiene dos soluciones complejas.

La ecuación cuadrática$\ x^{2}-4 x+10=0$ tiene dos soluciones complejas.

Ejercicio

Supongamos que una ecuación cuadrática tiene un discriminante que evalúa a cero. ¿Cuál de las siguientes afirmaciones es siempre cierta?

La ecuación tiene dos soluciones.
La ecuación tiene una solución.
La ecuación tiene cero soluciones.

Contestar

Incorrecto. Dado que sumar y restar 0 dan ambos el mismo resultado, la$\ \pm$ porción de la Fórmula Cuadrática no importa. Un discriminante de cero significa que la ecuación tiene una solución. La respuesta correcta es “La ecuación tiene una solución”.
Correcto. Un discriminante de cero significa que la ecuación tiene una solución.
Incorrecto. Cuando el discriminante es cero, la ecuación tendrá una solución. La respuesta correcta es “La ecuación tiene una solución”.

Aplicación de la Fórmula Cuadrática

Las ecuaciones cuadráticas son ampliamente utilizadas en ciencia, negocios e ingeniería. Las ecuaciones cuadráticas se utilizan comúnmente en situaciones en las que dos cosas se multiplican entre sí y ambas dependen de la misma variable. Por ejemplo, cuando se trabaja con área, si ambas dimensiones se escriben en términos de una misma variable, se usa una ecuación cuadrática. Debido a que la cantidad de un producto vendido a menudo depende del precio, a veces se utiliza una ecuación cuadrática para representar los ingresos como un producto del precio y la cantidad vendida. También se utilizan ecuaciones cuadráticas cuando está involucrada la gravedad, como la trayectoria de una bola o la forma de cables en un puente colgante.

Una aplicación muy común y fácil de entender es la altura de una pelota lanzada al suelo desde un edificio. Debido a que la gravedad hará que la pelota se acelere a medida que cae, se puede utilizar una ecuación cuadrática para estimar su altura en cualquier momento antes de que golpee el suelo. Nota: La ecuación no es completamente precisa, porque la fricción del aire ralentizará un poco la pelota. Para nuestros propósitos, esto es lo suficientemente cercano.

Ejemplo

Se lanza una pelota desde un edificio desde 200 pies sobre el suelo. Su velocidad inicial (también llamada velocidad inicial) es de -10 pies por segundo. (El valor negativo significa que se dirige hacia el suelo).

La ecuación se$\ h=-16 t^{2}-10 t+200$ puede utilizar para modelar la altura de la pelota después de$\ t$ segundos. Acerca de cuánto tiempo tarda la pelota en golpear el suelo?

Solución

\ (\\ begin {array} {l} h=-16 t^ {2} -10 t+200\\ 0=-16 t^ {2} -10 t+200\\ -16 t^ {2} -10 t+200=0 \ end {array}\)	Cuando la pelota golpea el suelo, la altura es 0. Sustituir 0 por$\ h$.
$\ t=\frac{-(-10) \pm \sqrt{(-10)^{2}-4(-16)(200)}}{2(-16)}$	Esta ecuación es difícil de resolver factorizando o completando el cuadrado, así que resuelva aplicando la Fórmula Cuadrática,$\ x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$. En este caso, la variable es$\ t$ más bien que$\ x$. $\ a=-16$,$\ b=-10$, y$\ c=200$.
\ (\\ comenzar {alineado} t &=\ frac {10\ pm\ sqrt {100+12,800}} {-32}\\ &=\ frac {10\ pm\ sqrt {12,900}} {-32} \ final {alineado}\)	Simplificar. Ten mucho cuidado con las señales. Usa una calculadora para encontrar ambas raíces.
$\ t$es aproximadamente$\ -3.86$ o$\ 3.24$.	Considera las raíces lógicamente. Una solución, -3.86, no puede ser el tiempo porque es un número negativo. La otra solución, 3.24 segundos, debe ser cuando la pelota golpea el suelo.

El balón golpea el suelo aproximadamente 3.24 segundos después de ser arrojado.

El problema de área a continuación no parece que incluya una Fórmula Cuadrática de ningún tipo, y el problema parece ser algo que has resuelto muchas veces antes simplemente multiplicando. Pero para resolverlo, necesitarás usar una ecuación cuadrática.

Ejemplo

Bob hizo una colcha que mide 4 pies por 5 pies. Tiene 10 pies cuadrados de tela que puede usar para agregar un borde alrededor de la colcha. ¿Qué tan ancho debe hacer el borde para usar toda la tela? (El borde debe tener el mismo ancho en los cuatro lados.)

Solución

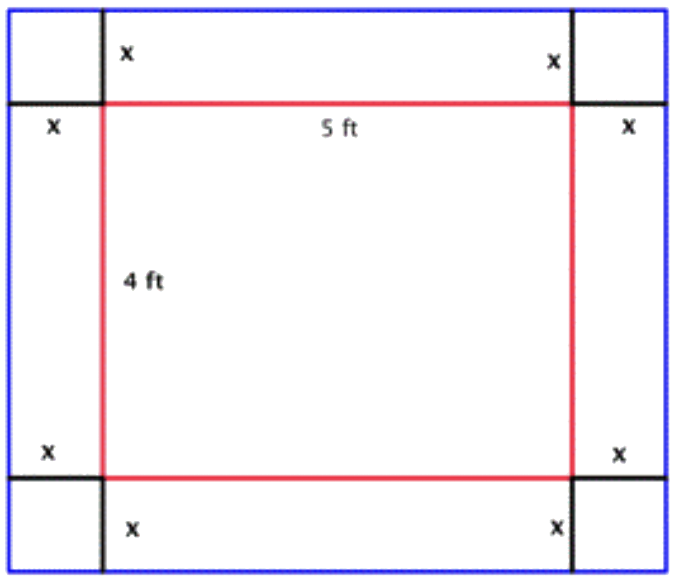$Screen Shot 2021-07-15 al 1.03.07 PM.png$	Esbozar el problema. Como no conoces el ancho del borde, dejarás que la variable$\ x$ represente el ancho. En el diagrama, la colcha original está indicada por el rectángulo rojo. El borde es el área entre las líneas roja y azul.
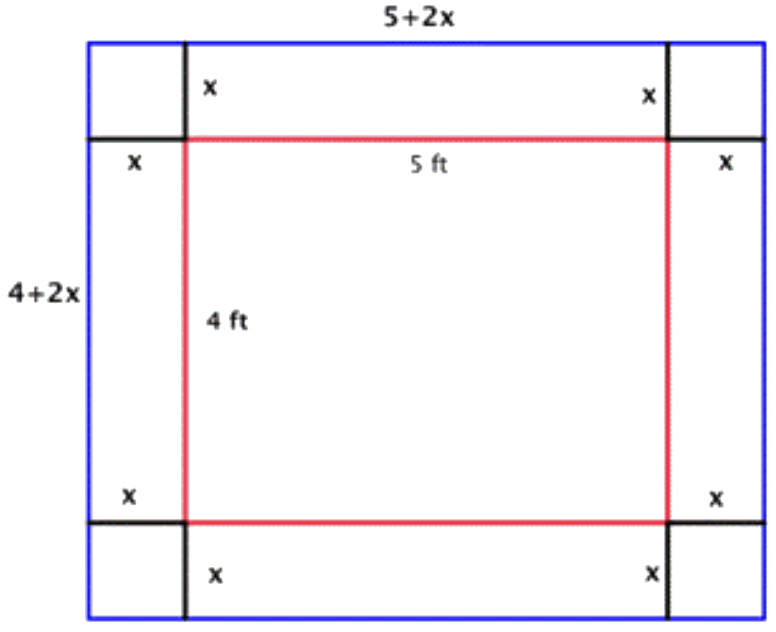$Screen Shot 2021-07-15 en 1.03.34 PM.png$	Dado que cada lado de la colcha original 4 por 5 tiene el borde de ancho$\ x$ agregado, la longitud de la colcha con el borde será$\ 5+2 x$, y la anchura será$\ 4+2 x$. (Ambas dimensiones están escritas en términos de una misma variable, ¡y las multiplicarás para obtener un área! Aquí es donde podrías empezar a pensar que se podría usar una ecuación cuadrática para resolver este problema).
Área de borde = Área del rectángulo azul menos el área del rectángulo rojo Zona de frontera$\ =(4+2 x)(5+2 x)-(4)(5)$	Solo te interesa la zona de las franjas fronterizas. Escribir una expresión para el área de la frontera.
$\ 10=(4+2 x)(5+2 x)-20$	Hay 10 pies cuadrados de tela para el borde, así que establece el área de borde en 10.
$\ 10=20+8 x+10 x+4 x^{2}-20$	Multiplicar$\ (4+2 x)(5+2 x)$.
$\ 10=18 x+4 x^{2}$	Simplificar.
\ (\\ begin {array} {r} 0=18 x+4 x^ {2} -10\\ \ texto {o}\\ 4 x^ {2} +18 x-10=0 \ end {array}\)	Resta 10 de ambos lados para que tengas una ecuación cuadrática en forma estándar y puedas aplicar la Fórmula Cuadrática para encontrar las raíces de la ecuación.
\ (\\ comenzar {alineado} 2\ izquierda (2 x^ {2} +9 x-5\ derecha) &=0\\ \ frac {2\ izquierda (2 x^ {2} +9 x-5\ derecha)} {2} &=\ frac {0} {2}\\ 2 x^ {2} +9 x-5 &=0 \ end {alineado}\)	Factorizar el mayor factor común, 2, para que puedas trabajar con la ecuación equivalente más simple,$\ 2 x^{2}+9 x-5=0$.
\ (\\ begin {array} {r} x=\ frac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\ x=\ frac {-9\ pm\ sqrt {9^ {2} -4 (2) (-5)}} {2 (2)} \ end {array}\)	Usa la Fórmula Cuadrática. En este caso,$\ a=2$,$\ b=9$, y$\ c=-5$.
$\ x=\frac{-9 \pm \sqrt{121}}{4}=\frac{-9 \pm 11}{4}$	Simplificar.
\ (\\ begin {array} {r} x=\ frac {-9+11} {4} =\ frac {2} {4} =\ frac {1} {2} =0.5\\ \ texto {o}\\ x=\ frac {-9-11} {4} =-\ frac {20} {4} =-5 \ end {array}\)	Encuentre las soluciones, asegurándose de que el$\ \pm$ sea evaluado para ambos valores.
El ancho del borde debe ser de 0.5 pies.	Ignorar la solución$\ x=-5$, ya que el ancho no podría ser negativo.

Ejercicio

Una pelota se lanza hacia arriba a 48 pies/segundo desde una plataforma que mide 100 pies de altura. La ecuación que da su altura$\ t$ segundos después del lanzamiento es$\ h=-16 t^{2}+48 t+100$. El balón disparará hasta 136 pies de altura, luego comenzará a volver a bajar. ¿Acerca de cuánto tiempo tardará la pelota en llegar a esa altura máxima?

1.5 segundos
3.6 segundos
4.4 segundos
Este problema no se puede resolver.

Contestar

Correcto. Cuando la altura es de 136 pies, la ecuación se vuelve$\ 136=-16 t^{2}+48 t+100$. Restar 136 de ambos lados da$\ 0=-16 t^{2}+48 t-36$. Factorizar -4 resultados en la ecuación más simple$\ 0=4 t^{2}-12 t+9$ y el uso de la Fórmula Cuadrática da$\ t=\frac{-(-12) \pm \sqrt{(-12)^{2}-4(4)(9)}}{2(4)}$. Esto simplifica a$\ t=\frac{12 \pm \sqrt{0}}{8}=1.5$. (Dado que el discriminante es 0, sólo hay una solución.) El balón alcanzará su altura máxima en 1.5 segundos.
Incorrecto. Probablemente configuraste la ecuación correctamente,$\ 136=-16 t^{2}+48 t+100$. Sin embargo, probablemente olvidaste un signo negativo para los valores de$\ a$ o$\ c$, o bien evaluaste incorrectamente$\ -4 a c$ en el discriminante. Restar 136 de ambos lados de la ecuación da$\ 0=-16 t^{2}+48 t-36$. Factorizar -4 resulta en la ecuación más simple$\ 0=4 t^{2}-12 t+9$, entonces$\ a=4$,$\ b=-12$, y$\ c=9$. Usando la Fórmula Cuadrática da$\ t=\frac{-(-12) \pm \sqrt{(-12)^{2}-4(4)(9)}}{2(4)}$. Esto simplifica a$\ t=\frac{12 \pm \sqrt{0}}{8}=1.5$. (Dado que el discriminante es 0, sólo hay una solución.) La respuesta correcta es de 1.5 segundos.
Incorrecto. Probablemente resolviste correctamente la ecuación$\ 0=-16 t^{2}+48 t+100$, pero estás buscando el momento en que la altura sea 136, no 0. La ecuación a resolver es$\ 136=-16 t^{2}+48 t+100$. Restar 136 de ambos lados da$\ 0=-16 t^{2}+48 t-36$. Factorizar -4 resultados en la ecuación más simple$\ 0=4 t^{2}-12 t+9$ y el uso de la Fórmula Cuadrática da$\ t=\frac{-(-12) \pm \sqrt{(-12)^{2}-4(4)(9)}}{2(4)}$. Esto simplifica a$\ t=\frac{12 \pm \sqrt{0}}{8}=1.5$. (Dado que el discriminante es 0, sólo hay una solución.) La respuesta correcta es de 1.5 segundos.
Incorrecto. Este problema se puede resolver si se sustituye 136 in por$\ h$ en la ecuación original. Esto te da:$\ 136=-16 t^{2}+48 t+100$. Restar 136 de ambos lados da$\ 0=-16 t^{2}+48 t-36$. Factorizar -4 resultados en la ecuación más simple$\ 0=4 t^{2}-12 t+9$ y el uso de la Fórmula Cuadrática da$\ t=\frac{-(-12) \pm \sqrt{(-12)^{2}-4(4)(9)}}{2(4)}$. Esto simplifica a$\ t=\frac{12 \pm \sqrt{0}}{8}=1.5$. (Dado que el discriminante es 0, sólo hay una solución.) La respuesta correcta es de 1.5 segundos.

Resumen

Las ecuaciones cuadráticas pueden aparecer en diferentes aplicaciones. La Fórmula Cuadrática es una manera útil de resolver estas ecuaciones, ¡o cualquier otra ecuación cuadrática! La Fórmula Cuadrática,$\ x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$, se encuentra completando el cuadrado de la ecuación cuadrática$\ a x^{2}+b x+c=0$.

El discriminante de la Fórmula Cuadrática es la cantidad bajo el radical,$\ b^{2}-4 a c$. Determina el número y el tipo de soluciones que tiene una ecuación cuadrática. Si el discriminante es positivo, hay 2 soluciones reales. Si es 0, hay 1 solución real. Si el discriminante es negativo, hay 2 soluciones complejas (pero no soluciones reales).

\(\ x^{2}+\frac{b}{a} x+\frac{c}{a}=0\)	Divide ambos lados de la ecuación por\(\ a\), de modo que el coeficiente de\(\ x^{2}\) sea 1.
\(\ x^{2}+\frac{b}{a} x=-\frac{c}{a}\)	Reescribe para que el lado izquierdo esté en la forma\(\ x^{2}+b x\), (aunque en este caso\(\ bx\) es en realidad\(\ \frac{b}{a} x\)).
\(\ x^{2}+\frac{b}{a} x+\left(\frac{b}{2 a}\right)^{2}=-\frac{c}{a}+\left(\frac{b}{2 a}\right)^{2}\)	El coeficiente on\(\ x\) es\(\ \frac{b}{a}\), por lo que el valor a sumar a ambos lados es\(\ \left(\frac{b}{2 a}\right)^{2}\).
\(\ \left(x+\frac{b}{2 a}\right)^{2}=-\frac{c}{a}+\left(\frac{b}{2 a}\right)^{2}\)	Escribe el lado izquierdo como un binomio cuadrado.
\(\ \left(x+\frac{b}{2 a}\right)^{2}=-\frac{c}{a}+\frac{b^{2}}{4 a^{2}}\)	Evaluar\(\ \left(\frac{b}{2 a}\right)^{2}\) como\(\ \frac{b^{2}}{4 a^{2}}\).
\(\ \left(x+\frac{b}{2 a}\right)^{2}=-\frac{4 a c}{4 a^{2}}+\frac{b^{2}}{4 a^{2}}\)	Escribe las fracciones del lado derecho usando un denominador común.
\(\ \left(x+\frac{b}{2 a}\right)^{2}=\frac{b^{2}-4 a c}{4 a^{2}}\)	Agrega las fracciones a la derecha.
\(\ x+\frac{b}{2 a}=\pm \sqrt{\frac{b^{2}-4 a c}{4 a^{2}}}\)	Utilice la Propiedad Raíz Cuadrada. ¡Recuerda que quieres tanto las raíces cuadradas positivas como las negativas!
\(\ x=-\frac{b}{2 a} \pm \sqrt{\frac{b^{2}-4 a c}{4 a^{2}}}\)	Restar\(\ \frac{b}{2 a}\) de ambos lados para aislar\(\ x\).
\(\ x=-\frac{b}{2 a} \pm \frac{\sqrt{b^{2}-4 a c}}{2 a}\)	El denominador bajo el radical es un cuadrado perfecto, entonces:\(\ \sqrt{\frac{b^{2}-4 a c}{4 a^{2}}}=\frac{\sqrt{b^{2}-4 a c}}{\sqrt{4 a^{2}}}=\frac{\sqrt{b^{2}-4 a c}}{2 a}\)
\(\ x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)	Sumar las fracciones ya que tienen un denominador común.

\ (\\ begin {array} {r} x^ {2} -2 x=6 x-16\\ x^ {2} -2 x-6 x+16=0\\ x^ {2} -8 x+16=0 \ end {array}\)	Restar\(\ 6x\) de cada lado y sumar 16 a ambos lados para poner la ecuación en forma estándar.
\ (\\ begin {array} {l} x^ {2}\ quad-&8 x\ quad+&16=0\\ \ flecha abajo&\ flecha abajo&\ flecha abajo\\ a x^ {2}\ quad+&b x\ quad+&c=0 \ end {array}\)	Identificar los coeficientes\(\ a\),\(\ b\), y\(\ c\). \(\ x^{2}=1 x^{2}\), entonces\(\ a=1\). Ya que\(\ 8x\) se resta,\(\ b\) es negativo. \(\ a=1, b=-8, c=16\)
\ (\\ begin {array} {c} x=\ frac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\ x=\ frac {- (-8)\ pm\ sqrt {(-8) ^ {2} -4 (1) (16)}} {2 (1)} \ end {array}\)	Sustituir los valores en la Fórmula Cuadrática.
\(\ x=\frac{8 \pm \sqrt{64-64}}{2}\)	Simplificar.
\(\ x=\frac{8 \pm \sqrt{0}}{2}=\frac{8}{2}=4\)	Dado que la raíz cuadrada de 0 es 0, y tanto sumar como restar 0 dan el mismo resultado, solo hay un valor posible.

\ (\\ begin {array} {r} b^ {2} -4 a c\\ (-4) ^ {2} -4 (1) (10) \ end {array}\)	Evaluar\(\ b^{2}-4 a c\). Primero tenga en cuenta que\(\ a=1\)\(\ b=-4\),, y\(\ c=10\).
\(\ 16-40=-24\)	El resultado es un número negativo. El discriminante es negativo, por lo que la ecuación cuadrática tiene dos soluciones complejas.

\ (\\ begin {array} {l} h=-16 t^ {2} -10 t+200\\ 0=-16 t^ {2} -10 t+200\\ -16 t^ {2} -10 t+200=0 \ end {array}\)	Cuando la pelota golpea el suelo, la altura es 0. Sustituir 0 por\(\ h\).
\(\ t=\frac{-(-10) \pm \sqrt{(-10)^{2}-4(-16)(200)}}{2(-16)}\)	Esta ecuación es difícil de resolver factorizando o completando el cuadrado, así que resuelva aplicando la Fórmula Cuadrática,\(\ x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\). En este caso, la variable es\(\ t\) más bien que\(\ x\). \(\ a=-16\),\(\ b=-10\), y\(\ c=200\).
\ (\\ comenzar {alineado} t &=\ frac {10\ pm\ sqrt {100+12,800}} {-32}\\ &=\ frac {10\ pm\ sqrt {12,900}} {-32} \ final {alineado}\)	Simplificar. Ten mucho cuidado con las señales. Usa una calculadora para encontrar ambas raíces.
\(\ t\)es aproximadamente\(\ -3.86\) o\(\ 3.24\).	Considera las raíces lógicamente. Una solución, -3.86, no puede ser el tiempo porque es un número negativo. La otra solución, 3.24 segundos, debe ser cuando la pelota golpea el suelo.