17.2.3: Búsqueda de dominio y rango

Última actualización
Guardar como PDF

Page ID: 111252

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Encuentra el dominio de una función de raíz cuadrada.
Encuentra el dominio y rango de una función a partir de la forma algebraica.

Introducción

Las funciones son una correspondencia entre dos conjuntos, llamados dominio y rango. Al definir una función, generalmente se indica qué tipo de números pueden ser$\ (f(x))$ los valores de dominio$\ (x)$ y rango. Pero incluso si dices que son números reales, eso no significa que todos los números reales puedan ser utilizados para$\ x$. Tampoco significa que todos los números reales puedan ser valores de función,$\ f(x)$. Puede haber restricciones en el dominio y el rango. Las restricciones dependen en parte del tipo de función.

En este tema, todas las funciones estarán restringidas a valores de números reales. Es decir, solo se pueden usar números reales en el dominio, y solo los números reales pueden estar en el rango.

Restringir el dominio

Hay dos razones principales por las que los dominios están restringidos.

No se puede dividir por 0.
No se puede tomar la raíz cuadrada (u otra raíz par) de un número negativo, ya que el resultado no será un número real.

¿En qué tipo de funciones se producirían estos dos temas?

La división por 0 podría ocurrir siempre que la función tenga una variable en el denominador de una expresión racional. Es decir, es algo que hay que buscar en las funciones racionales. ¡Mira estos ejemplos y observa que “división por 0” no significa necesariamente que$\ x$ sea 0!

Función	Notas
$\ f(x)=\frac{1}{x}$	Si$\ x=0$, estarías dividiendo por 0, entonces$\ x \neq 0$.
$\ f(x)=\frac{2+x}{x-3}$	Si$\ x=3$, estarías dividiendo por 0, entonces$\ x \neq 3$.
$\ f(x)=\frac{2(x-1)}{x-1}$	Aunque se puede simplificar esta función a$\ f(x)=2$, cuando$\ x=1$ la función original incluiría la división por 0. Entonces$\ x \neq 1$.
$\ f(x)=\frac{x+1}{x^{2}-1}$	Ambos$\ x=1$ y$\ x=-1$ harían el denominador 0. Nuevamente, esta función se puede simplificar a$\ f(x)=\frac{1}{x-1}$, pero cuando$\ x=1$ o$\ x=-1$ la función original incluiría la división por 0, así$\ x \neq 1$ y$\ x \neq-1$.
$\ f(x)=\frac{2(x-1)}{x^{2}+1}$	Este es un ejemplo sin restricciones de dominio, a pesar de que hay una variable en el denominador. Ya que$\ x^{2} \geq 0$, nunca$\ x^{2}+1$ puede ser 0. Lo mínimo que puede ser es 1, así que no hay peligro de división por 0.

Las raíces cuadradas de números negativos pueden ocurrir siempre que la función tenga una variable bajo un radical con una raíz par. ¡Mira estos ejemplos, y observa que “raíz cuadrada de una variable negativa” no significa necesariamente que el valor bajo el signo radical sea negativo! Por ejemplo, si$\ x=-4$, entonces$\ -x=-(-4)=4$, un número positivo.

Función	Restricciones al Dominio
$\ f(x)=\sqrt{x}$	Si$\ x<0$, estarías tomando la raíz cuadrada de un número negativo, entonces$\ x \geq 0$.
$\ f(x)=\sqrt{x+10}$	Si$\ x<-10$, estarías tomando la raíz cuadrada de un número negativo, entonces$\ x \geq-10$.
$\ f(x)=\sqrt{-x}$	¿Cuándo es$\ -x$ negativo? Sólo cuando$\ x$ es positivo. (Por ejemplo, si$\ x=-3$, entonces$\ -x=3$. Si$\ x=1$, entonces$\ -x=-1$.) Esto significa$\ x \leq 0$.
$\ f(x)=\sqrt{x^{2}-1}$	$\ x^{2}-1$debe ser positivo,$\ x^{2}-1>0$. Entonces$\ x^{2}>1$. Esto ocurre sólo cuando$\ x$ es mayor que 1 o menor que -1:$\ x \leq-1$ o$\ x \geq 1$.
$\ f(x)=\sqrt{x^{2}+10}$	No hay restricciones de dominio, a pesar de que hay una variable bajo el radical. Ya que$\ x^{2} \geq 0$, nunca$\ x^{2}+10$ puede ser negativo. Lo mínimo que puede ser es 10, por lo que no hay peligro de tomar la raíz cuadrada de un número negativo.

Los dominios pueden restringirse si:

la función es una función racional y el denominador es 0 para algún valor o valores de$\ x$
la función es una función radical con un índice par (como una raíz cuadrada), y el radicando puede ser negativo para algún valor o valores de$\ x$.

Rango

Recuerda, aquí el rango está restringido a todos los números reales. El rango también está determinado por la función y el dominio. Considera estas gráficas, y piensa en qué valores de$\ y$ son posibles, y qué valores (si los hay) no lo son. En cada caso, las funciones son de valor real: es decir,$\ x$ y sólo$\ f(x)$ pueden ser números reales.

Función cuadrática,$\ f(x)=x^{2}-2 x-3$

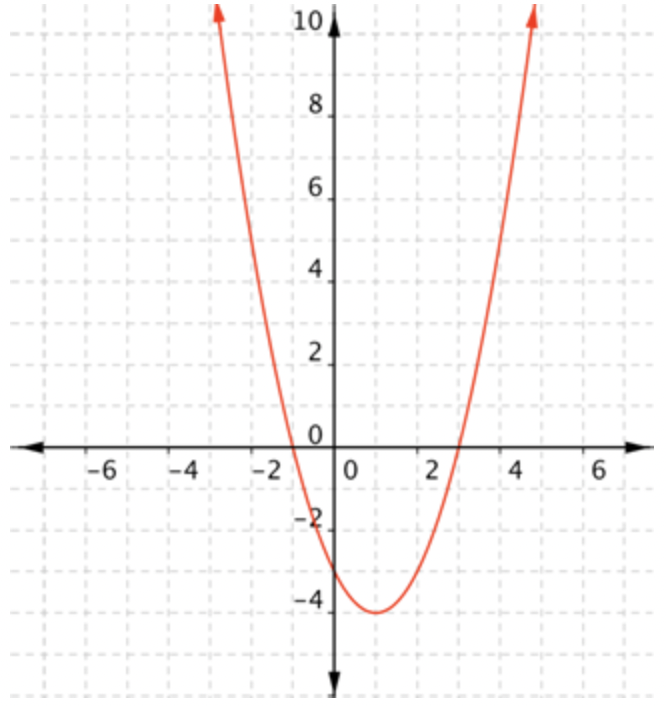
$Screen Shot 2021-07-16 a las 5.47.55 PM.png$

Recuerda la función cuadrática básica:$\ f(x)=x^{2}$ debe ser siempre positiva, así que$\ f(x) \geq 0$ en ese caso. En general, las funciones cuadráticas siempre tienen un punto con un valor máximo o mayor (si se abre hacia abajo) o un valor mínimo o mínimo (si se abre, como el anterior). Eso significa que el rango de una función cuadrática siempre estará restringido a estar por encima del valor mínimo o por debajo del valor máximo. Para la función anterior, el rango es$\ f(x) \geq-4$.

Otras funciones polinómicas con grados pares tendrán restricciones de alcance similares. Las funciones polinómicas con grados impares, como$\ f(x)=x^{3}$, no tendrán restricciones.

Función radical,$\ f(x)=-\sqrt{x}-2$

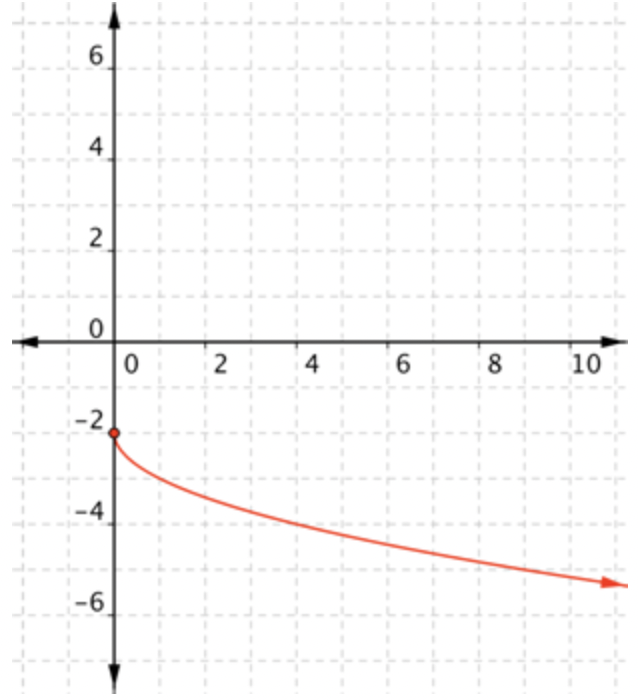
$Screen Shot 2021-07-16 a las 5.49.53 PM.png$

Las funciones de raíz cuadrada parecen la mitad de una parábola, girada de costado. El hecho de que la porción de raíz cuadrada siempre debe ser positiva restringe el rango de la función básica,$\ f(x)=\sqrt{x}$, a solo valores positivos. Los cambios en esa función, como el negativo frente al radical o la resta de 2, pueden cambiar el rango. El rango de la función anterior es$\ f(x) \leq-2$.

Función racional,$\ f(x)=\frac{x}{x-6}$

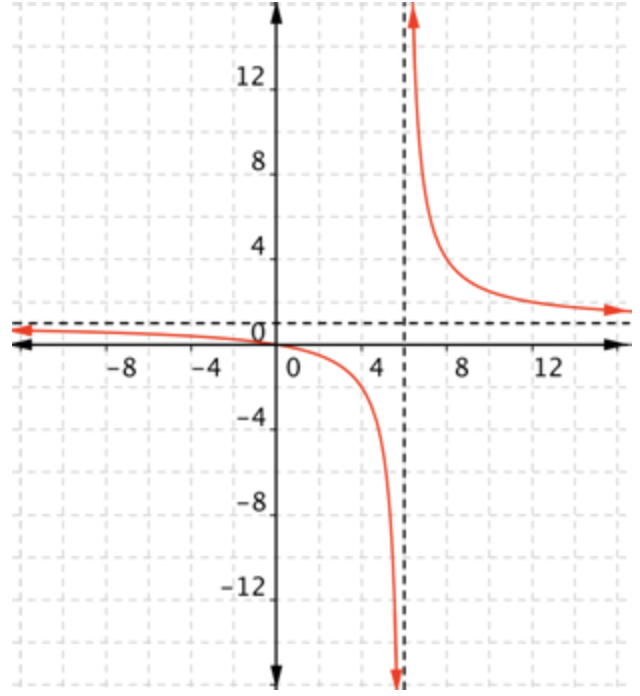
$Screen Shot 2021-07-16 a las 5.51.52 PM.png$

Las funciones racionales pueden parecer complicadas. No hay nada en la función que obviamente restrinja el rango. No obstante, las funciones racionales tienen asíntotas: líneas a las que la gráfica se acercará, pero nunca se cruzará ni siquiera tocará. En la gráfica anterior, la restricción de dominio proporciona una asíntota,$\ x=6$. El otro es la línea$\ y=1$, que proporciona una restricción al rango. En este caso, no hay valores de$\ x$ para los cuales$\ f(x)=1$. Entonces, el rango para esta función son todos los números reales excepto 1.

Determinar el dominio y el rango

Encontrar el dominio y rango de diferentes funciones suele ser cuestión de preguntarse, ¿qué valores puede no tener esta función?

Ejemplo

¿Cuáles son el dominio y el rango de la función de valor real$\ f(x)=x+3$?

Solución

Esta es una función lineal. Recuerda que las funciones lineales son líneas que continúan para siempre en cada dirección.

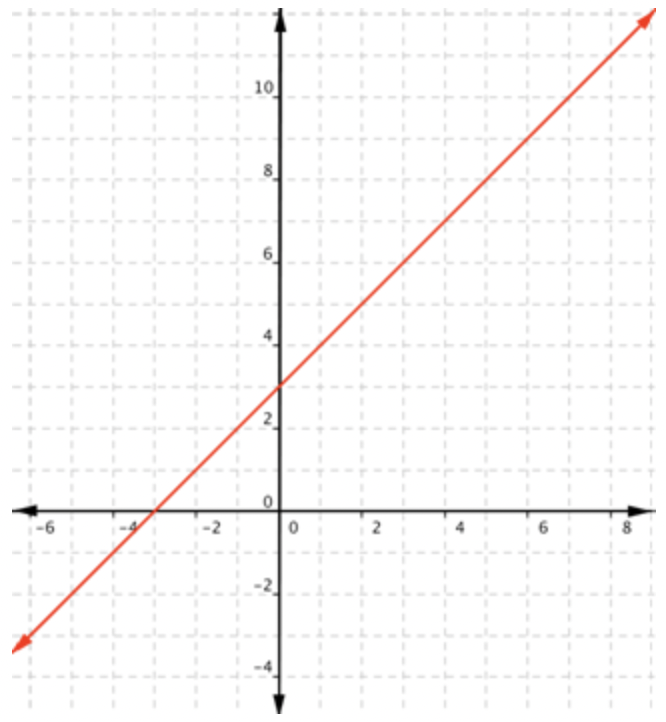
$Screen Shot 2021-07-16 a las 5.55.23 PM.png$

Cualquier número real puede ser sustituido$\ x$ y obtener una salida significativa. Para cualquier número real, siempre puedes encontrar un$\ x$ valor que te dé ese número para la salida. A menos que una función lineal sea una constante, como$\ f(x)=2$, no hay restricción en el rango.

El dominio y el rango son todos números reales.

Ejemplo

¿Cuáles son el dominio y el rango de la función de valor real$\ f(x)=-3 x^{2}+6 x+1$?

Solución

Esta es una función cuadrática. No hay expresiones racionales ni radicales, por lo que no hay nada que restrinja el dominio. Cualquier número real se puede utilizar$\ x$ para obtener una salida significativa.

Debido a que el coeficiente de$\ x^{2}$ es negativo, se abrirá a la baja. Con las funciones cuadráticas, recuerde que existe un valor máximo (mayor), o un valor mínimo (mínimo). En este caso, hay un valor máximo.

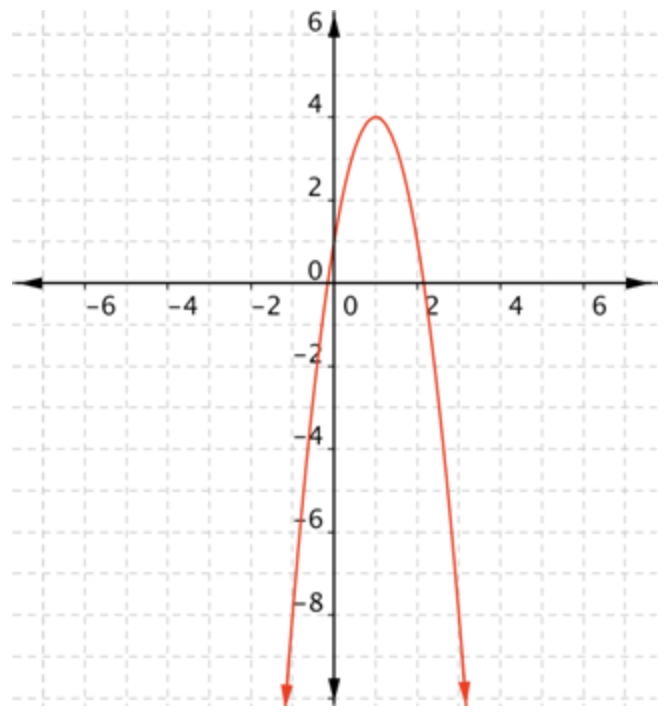
$Screen Shot 2021-07-16 at 5.58.32 PM.png$

El vértice, o punto de inflexión, está en$\ (1,4)$. De la gráfica, se puede ver eso$\ f(x) \leq 4$.

El dominio es todo números reales, y el rango es todo números reales$\ f(x)$ tales que$\ f(x) \leq 4$.

Se puede comprobar que el vértice está efectivamente en$\ (1,4)$. Dado que una función cuadrática tiene dos mitades de imagen especular, la línea de reflexión tiene que estar en medio de dos puntos con el mismo$\ y$ valor. El vértice debe estar en la línea de reflexión, ¡porque es el único punto que no tiene imagen especular!

En el ejemplo anterior, observe que cuando$\ x=2$ y cuando$\ x=0$, el valor de la función es 1. (Puede verificar esto evaluando$\ f(2)$ y$\ f(0)$.) Es decir, ambos$\ (2,1)$ y$\ (0,1)$ están en la gráfica. La línea de reflexión aquí es$\ x=1$, por lo que el vértice debe estar en el punto$\ \text { (1, } f(1)$). Evaluando$\ f(1)$ da$\ f(1)=4$, por lo que el vértice está en$\ (1,4)$.

Ejemplo

¿Cuáles son el dominio y el rango de la función de valor real$\ f(x)=-2+\sqrt{x+5}$?

Solución

Esta es una función radical. El dominio de una función radical es cualquier$\ x$ valor para el cual el radicando (el valor bajo el signo radical) no es negativo. Eso quiere decir$\ x+5 \geq 0$, entonces$\ x \geq-5$.

Ya que la raíz cuadrada siempre debe ser positiva o 0,$\ \sqrt{x+5} \geq 0$. Eso quiere decir$\ -2+\sqrt{x+5} \geq-2$.

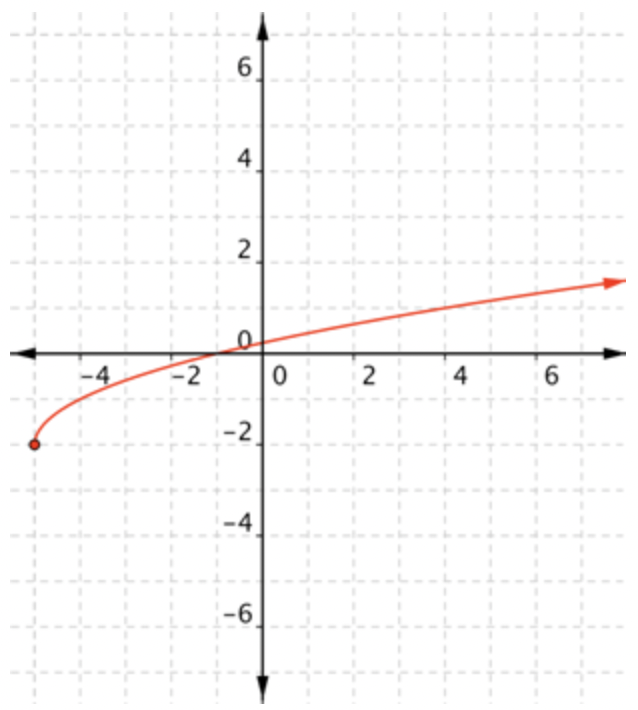
$Screen Shot 2021-07-16 a las 6.14.37 PM.png$

El dominio es todo números reales$\ x$ donde$\ x \geq-5$, y el rango es todo números reales$\ f(x)$ tales que$\ f(x) \geq-2$.

Ejemplo

¿Cuáles son el dominio y el rango de la función de valor real$\ f(x)=\frac{3 x}{x+2}$?

Solución

Esta es una función racional. El dominio de una función racional está restringido donde el denominador es 0. En este caso,$\ x+2$ es el denominador, y esto es 0 sólo cuando$\ x=-2$.

Para el rango, cree una gráfica usando una utilidad gráfica y busque asíntotas:

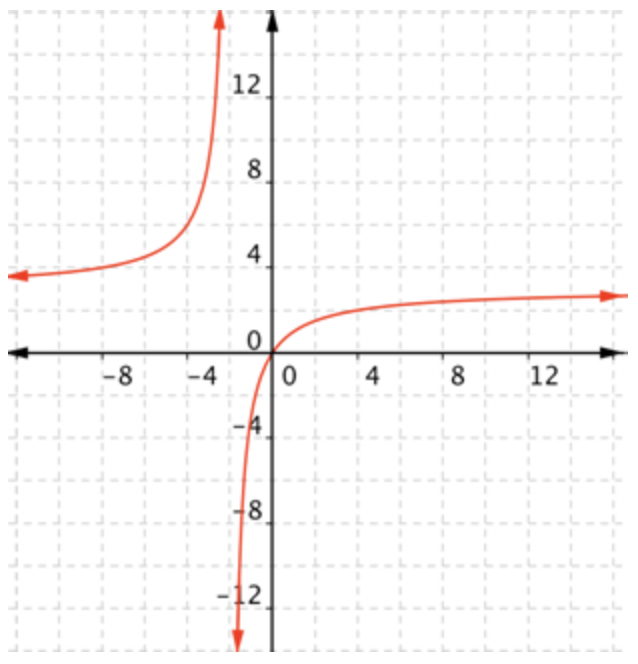
$Screen Shot 2021-07-16 a las 6.20.25 PM.png$

Una asíntota, una asíntota vertical, está en$\ x=-2$, como se debe esperar de la restricción de dominio. La otra, una asíntota horizontal, parece estar alrededor$\ y=3$. (De hecho, lo es$\ y=3$.)

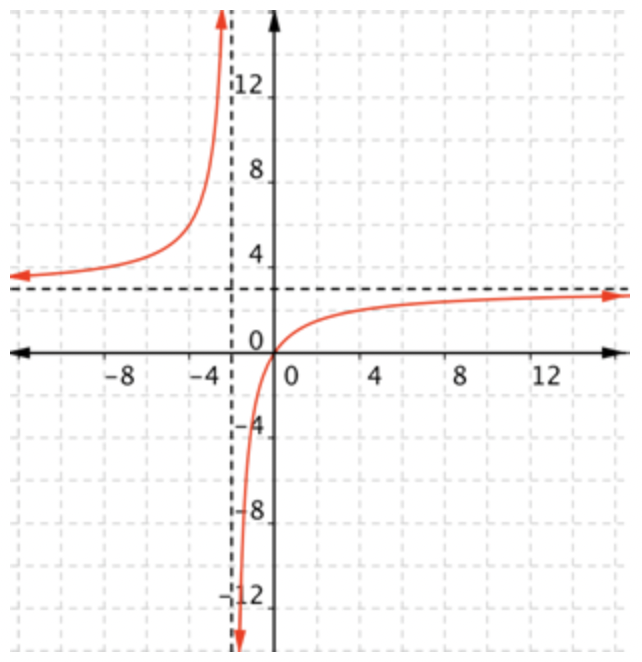
$Screen Shot 2021-07-16 at 6.22.16 PM.png$

El dominio es todos números reales excepto -2, y el rango es todos números reales excepto 3.

Se puede comprobar la asíntota horizontal,$\ y=3$. ¿Es posible$\ \frac{3 x}{x+2}$ que sea igual a 3? Escribe una ecuación y trata de resolverla.

\ (\\ begin {array} {c}
\ frac {3 x} {x+2} =3\\
(x+2)\ frac {3 x} {x+2} =( x+2) 3\\
3 x=3 x+6\\
0=6
\ end {array}\)

Dado que el intento de resolver termina con una declaración falsa, 0 no puede ser igual a 6, la ecuación no tiene solución. No hay valor$\ x$ para el cual$\ \frac{3 x}{x+2}=3$, por lo que esto demuestra que el rango está restringido.

Ejercicio

Encuentra el dominio y el rango de la función de valor real$\ f(x)=x^{2}+7$.

El dominio es todo números reales y el rango es todo números reales$\ f(x)$ tal que$\ f(x) \geq 7$.
El dominio es todo números reales$\ x$ tal que$\ x \geq 0$ y el rango es todo números reales$\ f(x)$ tales que$\ f(x) \geq 7$.
El dominio es todo números reales$\ x$ tal que$\ x \geq 0$ y el rango es todo números reales.
El dominio y el rango son todos números reales.

Contestar

El dominio es todo números reales y el rango es todo números reales$\ f(x)$ tal que$\ f(x) \geq 7$.
Correcto. Las funciones cuadráticas no tienen restricciones de dominio. Ya que$\ x^{2} \geq 0$,$\ x^{2}+7 \geq 7$.
El dominio es todo números reales$\ x$ tal que$\ x \geq 0$ y el rango es todo números reales$\ f(x)$ tales que$\ f(x) \geq 7$.
Incorrecto. Los valores negativos se pueden utilizar para$\ x$. La respuesta correcta es: El dominio es todo números reales y el rango es todo números reales$\ f(x)$ tal que$\ f(x) \geq 7$.
El dominio es todo números reales$\ x$ tal que$\ x \geq 0$ y el rango es todo números reales.
Incorrecto. Los valores negativos se pueden utilizar para$\ x$, pero el rango está restringido porque$\ x^{2} \geq 0$. La respuesta correcta es: El dominio es todo números reales y el rango es todo números reales$\ f(x)$ tal que$\ f(x) \geq 7$.
El dominio y el rango son todos números reales.
Incorrecto. Si bien es cierto que las funciones cuadráticas no tienen restricciones de dominio, el rango está restringido porque$\ x^{2} \geq 0$. La respuesta correcta es: El dominio es todo números reales y el rango es todo números reales$\ f(x)$ tal que$\ f(x) \geq 7$.

Resumen

Aunque una función puede ser dada como “valorada real”, puede ser que la función tenga restricciones a su dominio y rango. Puede haber algunos números reales que no pueden ser parte del dominio o parte del rango. Esto es particularmente cierto con funciones racionales y radicales, que pueden tener restricciones de dominio, rango, o ambos. Otras funciones, como las funciones cuadráticas y las funciones polinómicas de grado par, también pueden tener restricciones en su rango.

Función	Notas
\(\ f(x)=\frac{1}{x}\)	Si\(\ x=0\), estarías dividiendo por 0, entonces\(\ x \neq 0\).
\(\ f(x)=\frac{2+x}{x-3}\)	Si\(\ x=3\), estarías dividiendo por 0, entonces\(\ x \neq 3\).
\(\ f(x)=\frac{2(x-1)}{x-1}\)	Aunque se puede simplificar esta función a\(\ f(x)=2\), cuando\(\ x=1\) la función original incluiría la división por 0. Entonces\(\ x \neq 1\).
\(\ f(x)=\frac{x+1}{x^{2}-1}\)	Ambos\(\ x=1\) y\(\ x=-1\) harían el denominador 0. Nuevamente, esta función se puede simplificar a\(\ f(x)=\frac{1}{x-1}\), pero cuando\(\ x=1\) o\(\ x=-1\) la función original incluiría la división por 0, así\(\ x \neq 1\) y\(\ x \neq-1\).
\(\ f(x)=\frac{2(x-1)}{x^{2}+1}\)	Este es un ejemplo sin restricciones de dominio, a pesar de que hay una variable en el denominador. Ya que\(\ x^{2} \geq 0\), nunca\(\ x^{2}+1\) puede ser 0. Lo mínimo que puede ser es 1, así que no hay peligro de división por 0.

Función	Restricciones al Dominio
\(\ f(x)=\sqrt{x}\)	Si\(\ x<0\), estarías tomando la raíz cuadrada de un número negativo, entonces\(\ x \geq 0\).
\(\ f(x)=\sqrt{x+10}\)	Si\(\ x<-10\), estarías tomando la raíz cuadrada de un número negativo, entonces\(\ x \geq-10\).
\(\ f(x)=\sqrt{-x}\)	¿Cuándo es\(\ -x\) negativo? Sólo cuando\(\ x\) es positivo. (Por ejemplo, si\(\ x=-3\), entonces\(\ -x=3\). Si\(\ x=1\), entonces\(\ -x=-1\).) Esto significa\(\ x \leq 0\).
\(\ f(x)=\sqrt{x^{2}-1}\)	\(\ x^{2}-1\)debe ser positivo,\(\ x^{2}-1>0\). Entonces\(\ x^{2}>1\). Esto ocurre sólo cuando\(\ x\) es mayor que 1 o menor que -1:\(\ x \leq-1\) o\(\ x \geq 1\).
\(\ f(x)=\sqrt{x^{2}+10}\)	No hay restricciones de dominio, a pesar de que hay una variable bajo el radical. Ya que\(\ x^{2} \geq 0\), nunca\(\ x^{2}+10\) puede ser negativo. Lo mínimo que puede ser es 10, por lo que no hay peligro de tomar la raíz cuadrada de un número negativo.