17.2.2: Graficando Tipos de Funciones

Última actualización
Guardar como PDF

Page ID: 111253

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Gráfica funciones lineales.
Gráfica funciones cuadráticas.
Graficar funciones radicales.

Introducción

Cuando tanto la entrada (variable independiente) como la salida (variable dependiente) son números reales, una función puede ser representada por un gráfico de coordenadas. La entrada se traza en el eje x y la salida se traza en el eje y.

Funciones Lineales

Un primer paso útil para graficar una función es hacer una tabla de valores. Esto es particularmente útil cuando no se conoce la forma general que tendrá la función. Probablemente ya sepas que una función lineal será una línea recta, pero primero hagamos una tabla para ver cómo puede ser útil.

Al hacer una tabla, es una buena idea incluir valores negativos, valores positivos y cero para asegurarse de que tiene una función lineal.

Ejemplo

Hacer una tabla de valores para$\ f(x)=3 x+2$.

Solución

\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline & \ end {array}\)	Hacer una tabla de dos columnas. Etiquetar las columnas$\ x$ y$\ f(x)$.
\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline-2 &\\ -1 &\\ 0 &\\ 1 &\\ 3 & \ final {matriz}\)	Elija varios valores para$\ x$ y colóquelos como filas separadas en la$\ x$ columna. Consejo: Siempre es bueno incluir 0, valores positivos y valores negativos, si puedes.
\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline-2 & -4\\ -1 & -1\\ 0 & 2\\ 1 & 5\\ 3 & 11 \ end {array}\)	Evalúe la función para cada valor de$\ x$, y escriba el resultado en la$\ f(x)$ columna junto al$\ x$ valor que utilizó. Cuándo$\ x=0, f(0)=3(0)+2=2$,$\ f(1)=3(1)+2=5$,$\ f(-1)=3(-1)+2=-3+2=-1$ y así sucesivamente.
\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline-2 & -4\\ -1 & -1\\ 0 & 2\\ 1 & 5\\ 3 & 11 \ end {array}\)	(Tenga en cuenta que su tabla de valores puede ser diferente de la de otra persona. Cada uno puede elegir diferentes números para$\ x$.)

Ahora que tienes una tabla de valores, puedes utilizarlos para ayudarte a dibujar tanto la forma como la ubicación de la función. Importante: La gráfica de la función mostrará todos los valores posibles de$\ x$ y los valores correspondientes de$\ y$. Es por ello que la gráfica es una línea y no sólo los puntos que componen los puntos en nuestra tabla.

Ejemplo

Gráfica$\ f(x)=3 x+2$.

Solución

\ (\\ begin {array} {c|c}
x & f (x)\\
\ hline-2 & -4\\
-1 & -1\\
0 & 2\\
1 & 5\\
3 & 11
\ end {array}\)

Comienza con una tabla de valores, como la del ejemplo anterior.

Si piensas en eso$\ y$, cada fila forma un par ordenado que puedes trazar en una cuadrícula de coordenadas.$\ f(x)$

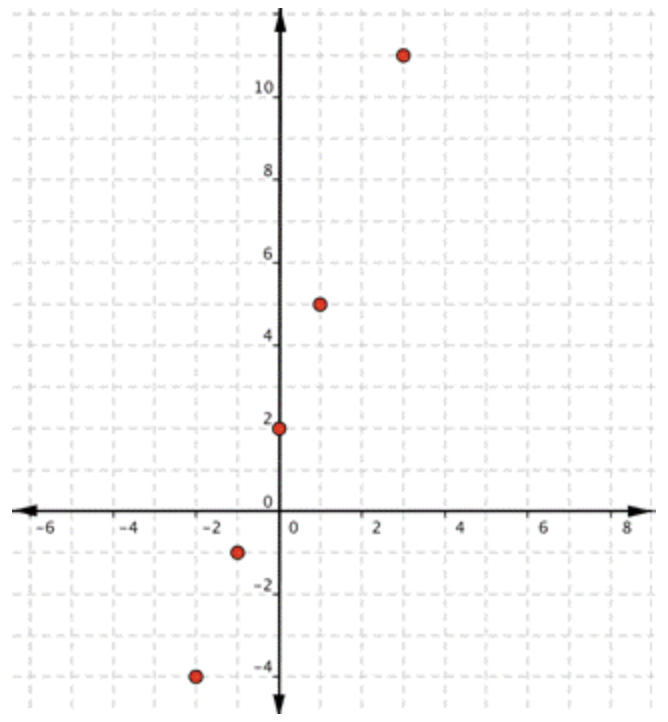$Screen Shot 2021-07-16 a las 12.26.17 AM.png$

Trazar los puntos.

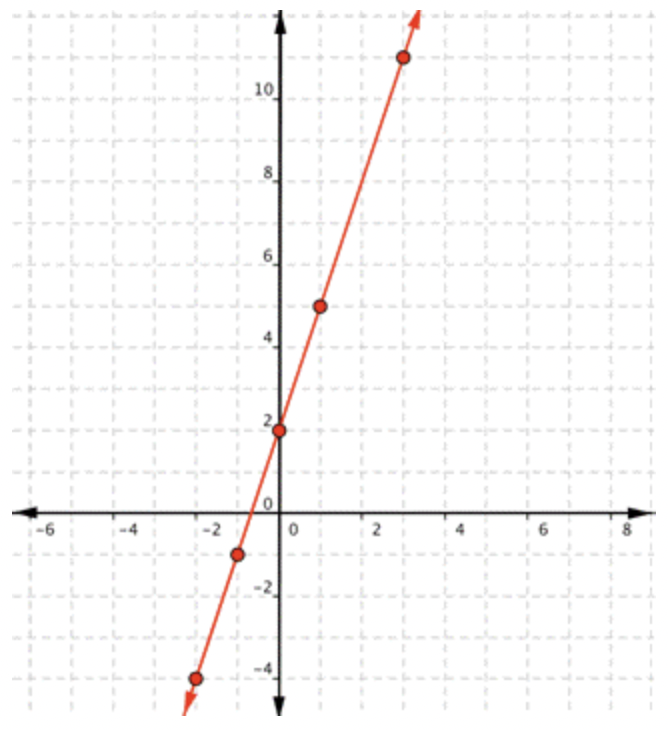$Screen Shot 2021-07-16 a las 12.27.07 AM.png$

Dado que los puntos se encuentran en una línea, use un borde recto para dibujar la línea. Intenta atravesar cada punto sin mover el borde recto.

Intentemos con otro.

Ejemplo

Gráfica$\ f(x)=-x+1$.

Solución

\ (\\ begin {array} {c}
f (-2) =- (-2) +1=2+1=3\\
f (-1) =- (-1) +1=1+1=2\\
f (0) =- (0) +1=0+1=1\\
f (1) =- (1) +1=-1+1=0\\
f (2) =- (2) +1=-2+1=-1
\ end {array}\)

\ (\\ begin {array} {c|c}
x & f (x)\\
\ hline-2 & 3\\
-1 & 2\\
0 & 1\\
1 & 0\\
2 & -1
\ end {array}\)

Comience con una tabla de valores. Puedes elegir diferentes valores para$\ x$, pero una vez más, es útil incluir 0, algunos valores positivos y algunos valores negativos. Si piensas que$\ y$, cada fila forma un par ordenado que puedes trazar en una cuadrícula de coordenadas.$\ f(x)$

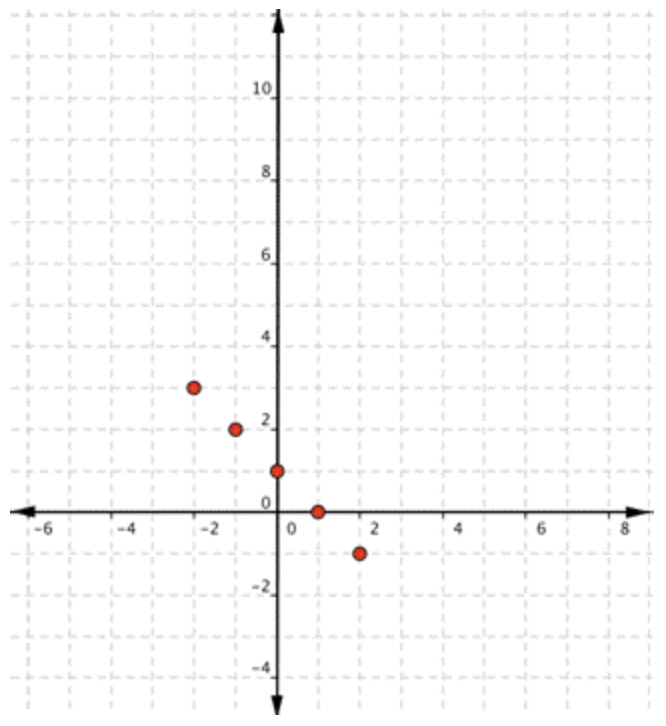$Screen Shot 2021-07-16 a las 12.31.06 AM.png$

Trazar los puntos.

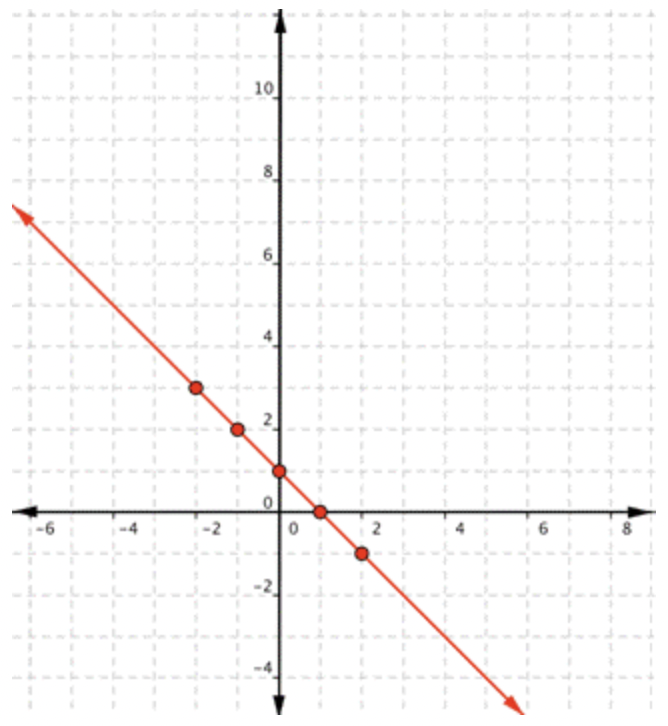$Screen Shot 2021-07-16 at 12.31.53 AM.png$

Dado que los puntos se encuentran en una línea, use un borde recto para dibujar la línea. Intenta atravesar cada punto sin mover el borde recto.

Estas gráficas son representaciones de una función lineal. Recuerde que una función es una correspondencia entre dos variables, como$\ x$ y$\ y$.

Ejercicio

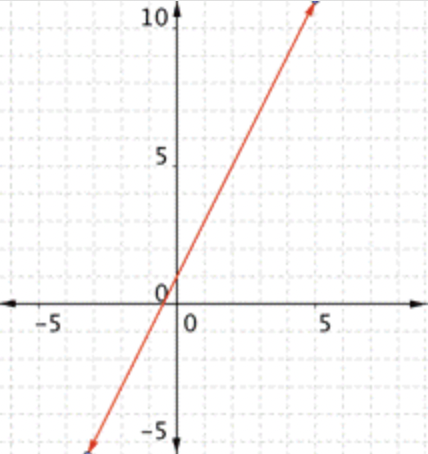
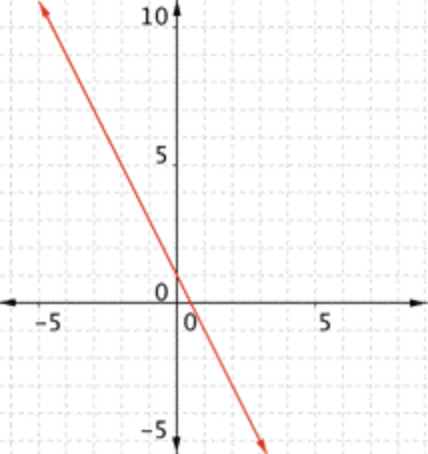
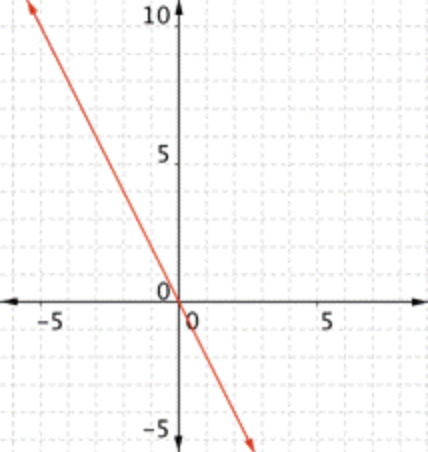
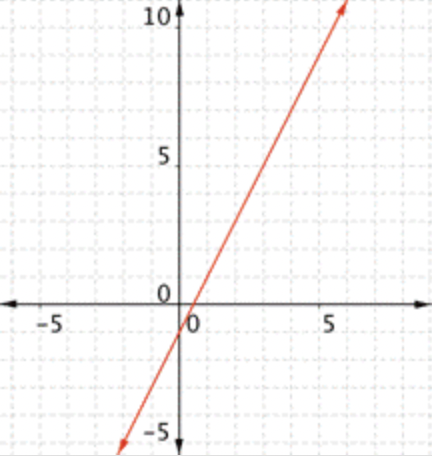
Gráfica$\ f(x)=2 x-1$. ¿Cuál de las siguientes gráficas es la correcta?

$Screen Shot 2021-07-16 a las 12.35.30 AM.png$
$Screen Shot 2021-07-16 a las 12.35.49 AM.png$
$Screen Shot 2021-07-16 a las 12.36.12 AM.png$
$Screen Shot 2021-07-16 a las 12.36.31 AM.png$

Contestar

Incorrecto.
Dos buenos puntos a verificar son cuándo$\ x=0$ y cuándo$\ y=0$. En este caso, eso sería$\ (0,-1)$ y$\ \left(\frac{1}{2}, 0\right)$. La respuesta correcta es Gráfica D.
Incorrecto.
Dos buenos puntos a verificar son cuándo$\ x=0$ y cuándo$\ y=0$. En este caso, eso sería$\ (0,-1)$ y$\ \left(\frac{1}{2}, 0\right)$. La respuesta correcta es Gráfica D.
Incorrecto.
Dos buenos puntos a verificar son cuándo$\ x=0$ y cuándo$\ y=0$. En este caso, eso sería$\ (0,-1)$ y$\ \left(\frac{1}{2}, 0\right)$. La respuesta correcta es Gráfica D.
Correcto.
Dos buenos puntos a verificar son cuándo$\ x=0$ y cuándo$\ y=0$. En este caso, eso sería$\ (0,-1)$ y$\ \left(\frac{1}{2}, 0\right)$. Entonces, la Gráfica D es la respuesta correcta.

Funciones cuadráticas

Las funciones no lineales también se pueden graficar. Es útil tener una idea de cuál debe ser la forma, para que puedas estar seguro de que has elegido suficientes puntos para trazar como guía. Empecemos con la función cuadrática más básica,$\ f(x)=x^{2}$.

Ejemplo

Gráfica$\ f(x)=x^{2}$.

Solución

\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline-2 & 4\\ -1 & 1\\ 0 & 0\\ 1 & 1\\ 2 & 4 \ end {array}\)	Comience con una tabla de valores. Entonces piensa en la mesa como pares ordenados.
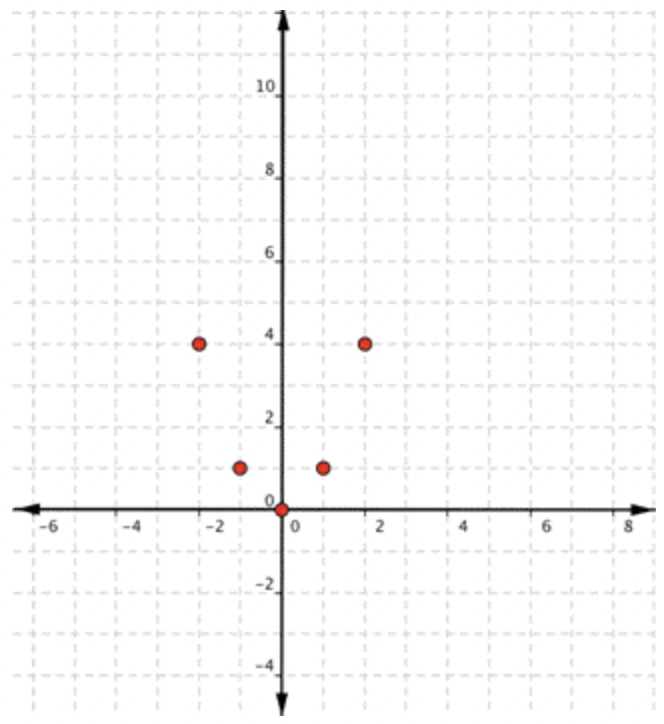$Screen Shot 2021-07-16 a las 12.48.31 AM.png$	Trazar los puntos.
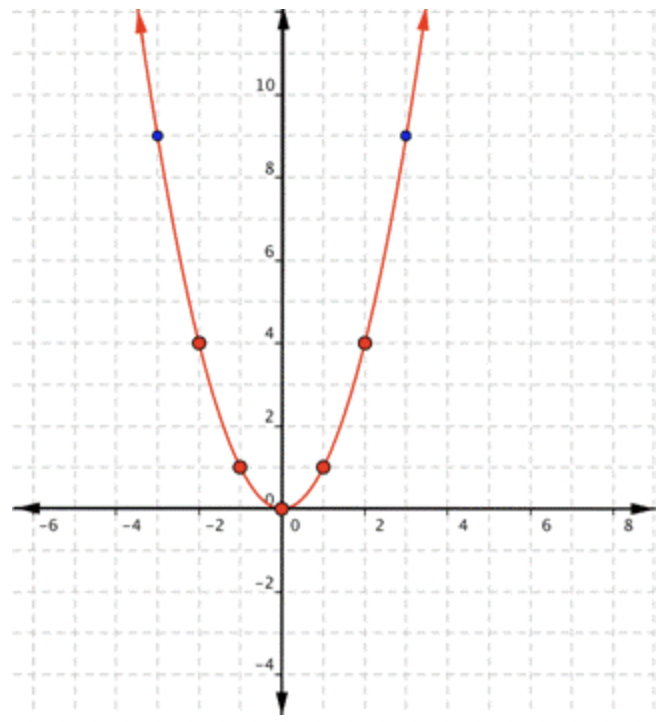$Screen Shot 2021-07-16 a las 12.49.12 AM.png$	Dado que los puntos no están en una línea, no se puede usar un borde recto. Conecta los puntos lo mejor que puedas, usando una curva suave (no una serie de líneas rectas). Es posible que desee encontrar y trazar puntos adicionales (como los que están en azul aquí).

Observe que la forma es como la letra U. Esto se llama parábola. La mitad de la parábola es una imagen especular de la otra mitad. A la línea que baja por el medio se le llama la línea de reflexión. En este caso esa línea es el eje y.

Las ecuaciones para funciones cuadráticas tienen la forma$\ f(x)=a x^{2}+b x+c$ donde$\ a \neq 0$. En la gráfica básica anterior,$\ a=1$,$\ b=0$, y$\ c=0$. Aquí hay algunas gráficas con diferentes valores para$\ a$,$\ b$, y$\ c$. Observe cómo cada valor cambia la forma y ubicación de la parábola.

Cambiando$\ a$ cambia el ancho de la parábola y si se abre hacia arriba$\ (a>0)$ o hacia abajo$\ (a<0)$.

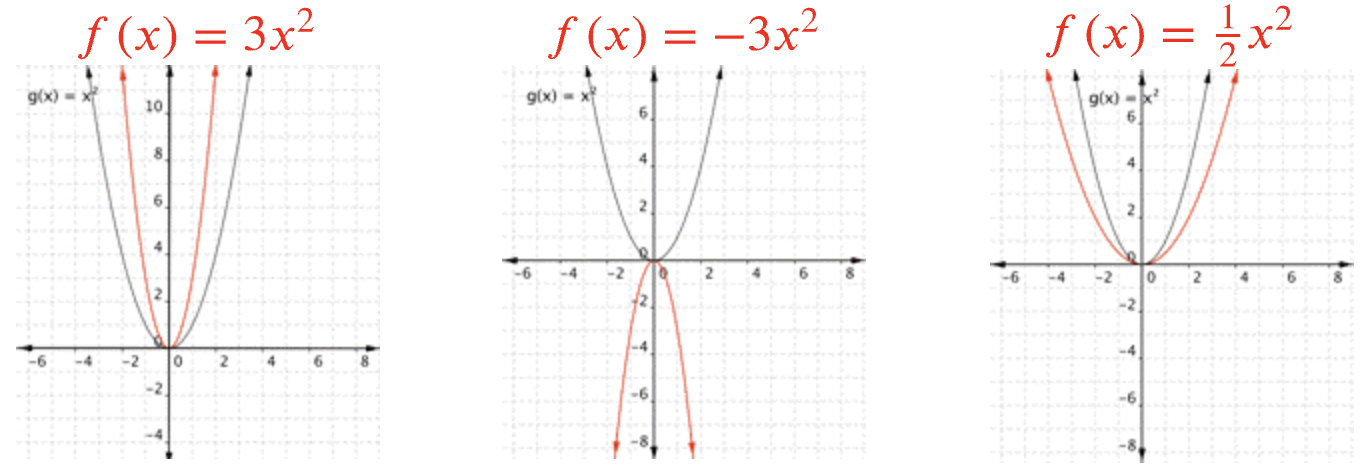
$Screen Shot 2021-07-16 a las 12.55.36 AM.png$

Si no hay$\ b$ término, el cambio$\ c$ mueve la parábola hacia arriba o hacia abajo para que la$\ y$ interceptación sea$\ (0, c)$.

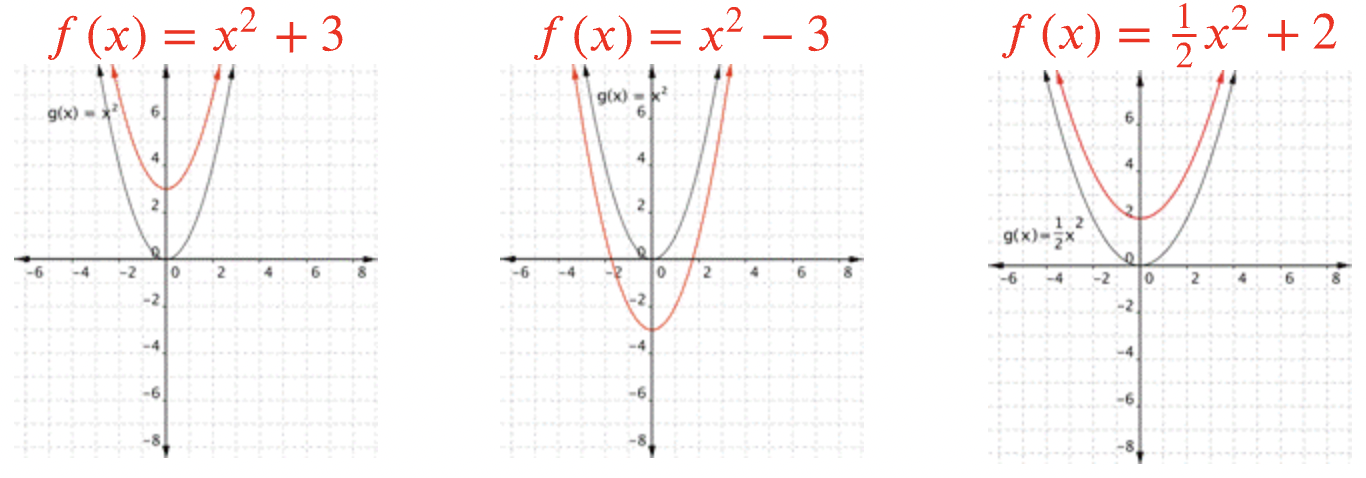
$Screen Shot 2021-07-16 a las 12.57.20 AM.png$

El cambio$\ b$ mueve la línea de reflexión. La forma en que se mueve depende también de$\ a$.

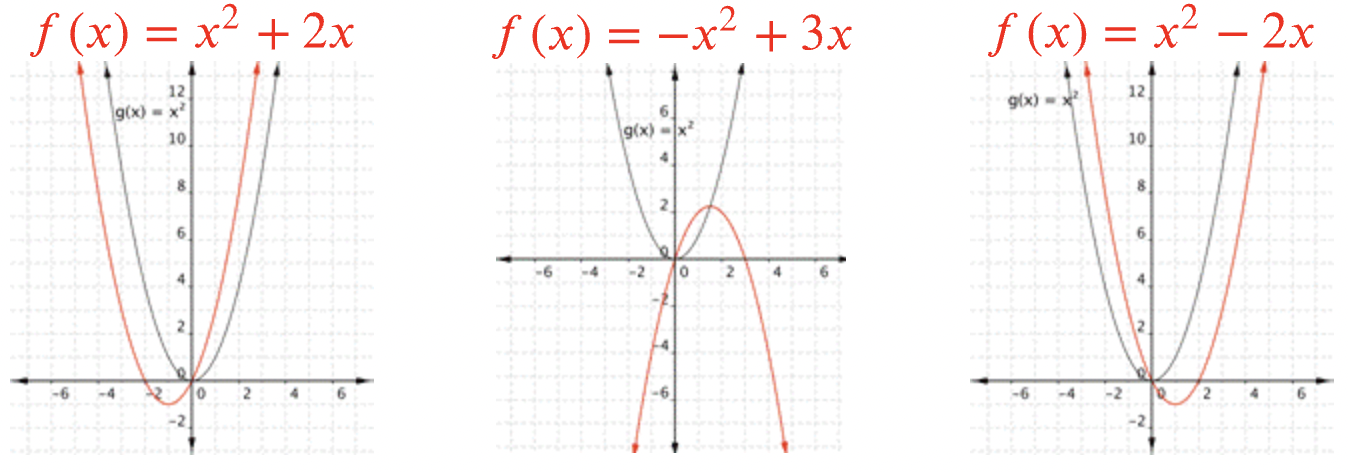
$Screen Shot 2021-07-16 a las 12.58.32 AM.png$

Propiedades de una Parabola

Para$\ f(x)=a x^{2}+b x+c$, donde$\ a$,$\ b$, y$\ c$ son números reales.

La parábola se abre hacia arriba si$\ a>0$ y hacia abajo si$\ a<0$.
$\ a$cambia el ancho de la parábola. La parábola se vuelve más estrecha si$\ |a|>1$ y más ancha si$\ |a|<1$.
El vértice depende de los valores de$\ a$,$\ b$, y$\ c$. El vértice es$\ \left(\frac{-b}{2 a}, f\left(\frac{-b}{2 a}\right)\right)$.

Ejemplo

Gráfica$\ f(x)=-2 x^{2}+3 x-3$.

Solución

$\ a=-2$, por lo que la gráfica se abrirá hacia abajo y será más delgada que$\ f(x)=x^{2}$. $\ c=-3$, por lo que se moverá para interceptar el eje y en$\ (0,-3)$.	Antes de hacer una tabla de valores, mira los valores de$\ a$ y$\ c$ para tener una idea general de cómo debería ser la gráfica.
\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline-2 & -17\\ -1 & -8\\ 0 & -3\\ 1 & -2\\ 2 & -5 \ end {array }\)	Crear una tabla de valores. Observe que en esta tabla, los$\ x$ valores aumentan. Los$\ y$ valores aumentan y luego comienzan a disminuir de nuevo. Eso indica una parábola.
$\ \text { Vertex formula }=\left(\frac{-b}{2 a}, f\left(\frac{-b}{2 a}\right)\right)$ coordenada x del vértice:$\ \frac{-b}{2 a}=\frac{-(3)}{2(-2)}=\frac{-3}{-4}=\frac{3}{4}$ coordenada y del vértice: \ (\\ begin {array} {r} f\ left (\ frac {-b} {2 a}\ right) =f\ left (\ frac {3} {4}\ right)\ f\ left (\ frac {3} {4}\ right) =-2\ left (\ frac {3} {4}\ right) ^ {2} +3\ left (\ frac {3}} {4}\ derecha) -3\\ =-2\ izquierda (\ frac {9} {16}\ derecha) +\ frac {9} {4} -3\\ =\ frac {-18} {16} +\ frac {9} {4} -3\\ =\ frac {-9} {8} +\ frac {18} {8} -\ frac {24} {8} {8}\ =-\ frac {15} {8} \ end {array}\) Vértice:$\ \left(\frac{3}{4},-\frac{15}{8}\right)$	Para encontrar el vértice de la parábola, usa la fórmula$\ \left(\frac{-b}{2 a}, f\left(\frac{-b}{2 a}\right)\right)$. Encontrar el vértice puede facilitar la representación gráfica de la parábola.
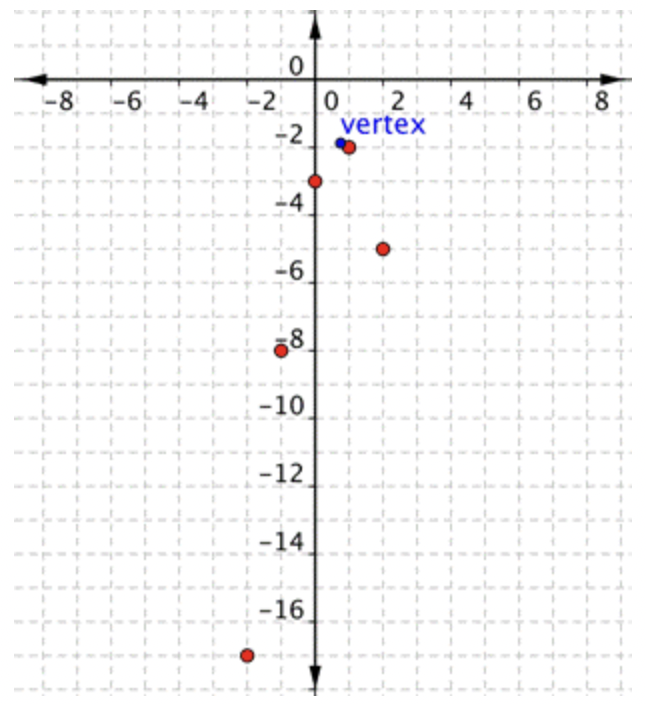$Screen Shot 2021-07-16 en 1.48.27 PM.png$	Utilice los pares de tablas para trazar puntos. Anote el vértice,$\ \left(\frac{3}{4},-\frac{15}{8}\right)$, en azul.
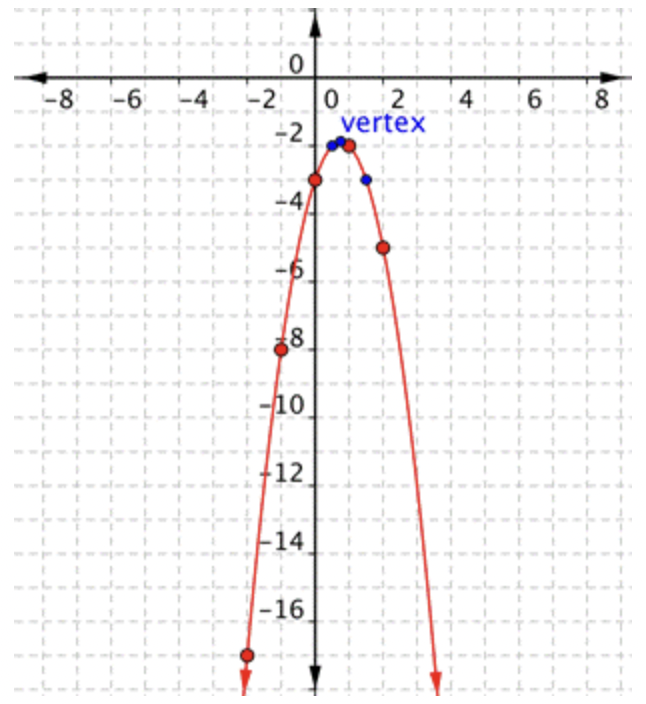$Screen Shot 2021-07-16 en 1.49.34 PM.png$	Conecta los puntos lo mejor que puedas, usando una curva suave. Recuerda que la parábola son dos imágenes especulares, así que si tus puntos no tienen pares con el mismo valor, es posible que quieras incluir puntos adicionales (como los que están en azul aquí). Trazar puntos a cada lado del vértice. $\ x=\frac{1}{2}$y$\ x=\frac{3}{2}$ son buenos valores para incluir.

Ejercicio

¿La gráfica se$\ f(x)=-3 x^{2}+2 x-1$ abriría hacia arriba o hacia abajo, y por qué?

Arriba, porque$\ a$ (el coeficiente de$\ x^{2}$) es negativo.
Abajo, porque$\ a$ (el coeficiente de$\ x^{2}$) es negativo.
Arriba, porque$\ b$ (el coeficiente de$\ x$) es positivo.
Abajo, porque$\ b$ (el coeficiente de$\ x$) es positivo.

Contestar

Arriba, porque$\ a$ (el coeficiente de$\ x^{2}$) es negativo.
Incorrecto. El coeficiente de$\ x^{2}$ es el lugar correcto para mirar, pero un coeficiente negativo significa que la gráfica se abre hacia abajo. La respuesta correcta es abajo, porque$\ a$ (el coeficiente de$\ x^{2}$) es negativo.
Abajo, porque$\ a$ (el coeficiente de$\ x^{2}$) es negativo.
Correcto. Un coeficiente negativo de$\ x^{2}$ medias que la gráfica abre hacia abajo.
Arriba, porque$\ b$ (el coeficiente de$\ x$) es positivo.
Incorrecto. Mira el coeficiente para$\ x^{2}$, no el coeficiente para$\ x$. La respuesta correcta es abajo, porque$\ a$ (el coeficiente de$\ x^{2}$) es negativo.
Abajo, porque$\ b$ (el coeficiente de$\ x$) es positivo.
Incorrecto. Mira el coeficiente para$\ x^{2}$, no el coeficiente para$\ x$. La respuesta correcta es abajo, porque$\ a$ (el coeficiente de$\ x^{2}$) es negativo.

Funciones radicales

También puede graficar funciones radicales (como las funciones de raíz cuadrada) eligiendo valores para$\ x$ y encontrando puntos que estarán en la gráfica. Nuevamente, es útil tener alguna idea sobre cómo será la gráfica.

Piense en la función básica de raíz cuadrada,$\ f(x)=\sqrt{x}$. Echemos un vistazo a una tabla de valores para$\ x$$\ y$ y luego graficemos la función. (Observe que todos los valores para$\ x$ en la tabla son cuadrados perfectos. Ya que estás tomando la raíz cuadrada de$\ x$, usar cuadrados perfectos tiene más sentido que solo encontrar las raíces cuadradas de 0 ,1, 2 ,3 ,4, etc.)

$\ x$	$\ f(x)$
0	0
1	1
4	2
9	3
16	4

Recordemos que aquí nunca$\ x$ puede ser negativo porque la raíz cuadrada de un número negativo sería imaginaria, y los números imaginarios no se pueden graficar. Tampoco hay valores para$\ x$ eso resultará en$\ y$ ser un número negativo. Echa un vistazo a la gráfica.

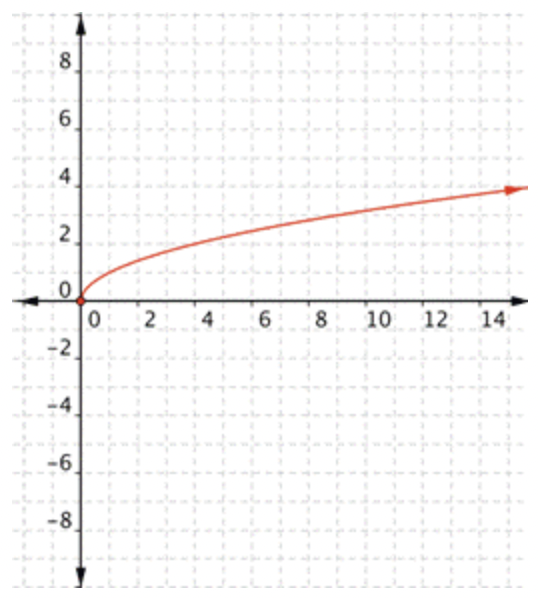
$Screen Shot 2021-07-16 a las 2.07.48 PM.png$

Al igual que con las paráolas, multiplicar y sumar números hace algunos cambios, pero la forma básica sigue siendo la misma. Aquí hay algunos ejemplos.

$\ \sqrt{x}$Al multiplicar por un valor positivo, se cambia el ancho de la media parábola. Multiplicar$\ \sqrt{x}$ por un número negativo te da la otra mitad de una parábola horizontal.

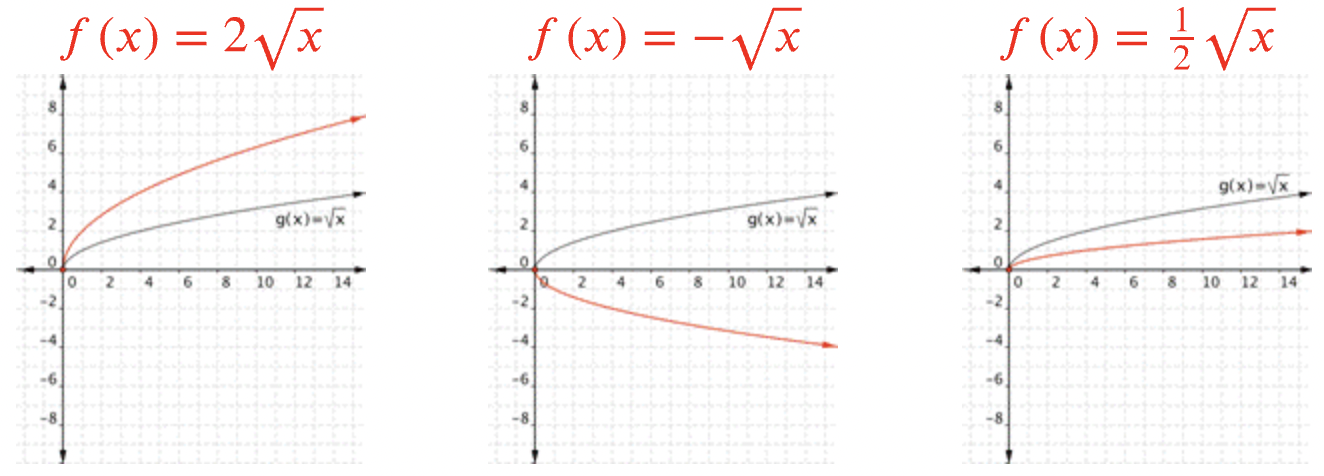
$Screen Shot 2021-07-16 a las 2.14.11 PM.png$

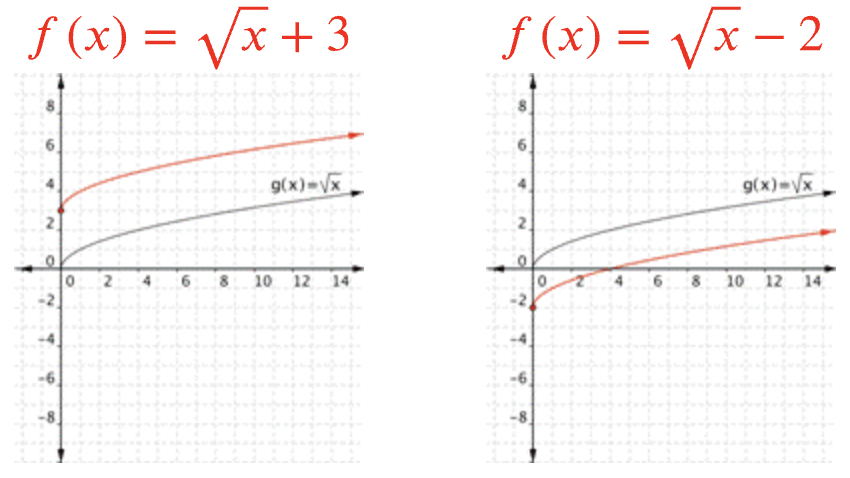
Agregar un valor fuera del radical mueve la gráfica hacia arriba o hacia abajo. Piense en ello como agregar el valor al$\ y$ valor básico de$\ \sqrt{x}$, por lo que un valor agregado positivo mueve la gráfica hacia arriba.

$Screen Shot 2021-07-16 a las 2.15.53 PM.png$

Agregar un valor dentro del radical mueve la gráfica hacia la izquierda o hacia la derecha. Piense en ello como agregar un valor$\ x$ antes de tomar la raíz cuadrada, por lo que el$\ y$ valor se mueve a un$\ x$ valor diferente. Por ejemplo, para$\ f(x)=\sqrt{x}$, la raíz cuadrada es 3 si$\ x=9$. Porque$\ f(x)=\sqrt{x+1}$, la raíz cuadrada es 3 cuando$\ x+1$ es 9, así$\ x$ es 8. Cambiar$\ x$ a$\ x+1$ desplaza la gráfica a la izquierda en 1 unidad (de 9 a 8). Cambiar$\ x$ a$\ x-2$ desplaza la gráfica hacia la derecha en 2 unidades.

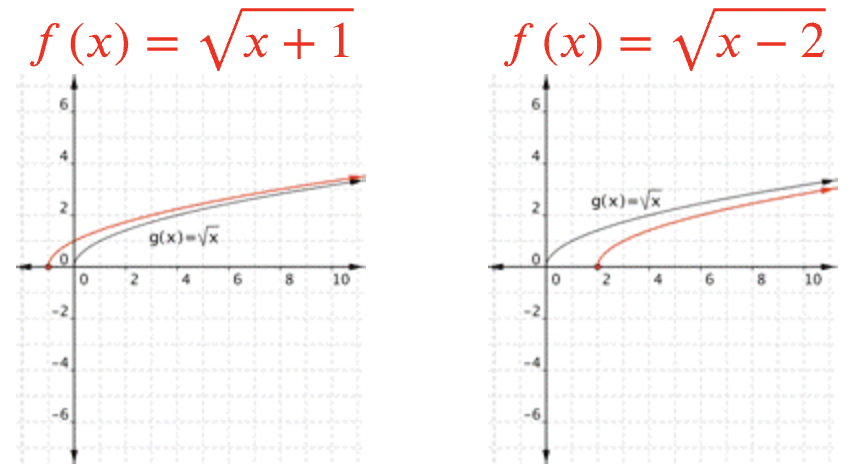
$Screen Shot 2021-07-16 a las 2.22.29 PM.png$

Observe que a medida$\ x$ que aumenta, sumar o restar un número dentro de la raíz cuadrada tiene menos efecto en el valor de$\ y$!

Ejemplo

Gráfica$\ f(x)=-2+\sqrt{x-1}$.

Solución

Dentro de la raíz cuadrada, estás restando 1, por lo que la gráfica se moverá a la derecha 1 de la$\ f(x)=\sqrt{x}$ gráfica básica. También estás agregando -2 fuera de la raíz cuadrada, por lo que la gráfica se moverá dos hacia abajo desde la$\ f(x)=\sqrt{x}$ gráfica básica.	Antes de hacer una tabla de valores, mira la ecuación de la función para tener una idea general de cómo debería ser la gráfica.
\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline 1 & -2\\ 2 & -1\\ 5 & 0\\ 10 & 1 \ end {array}\)	Crear una tabla de valores. Elige valores que faciliten tus cálculos. $\ x-1$Quieres ser un cuadrado perfecto, como 0, 1, 4, 9, y así sucesivamente, para que puedas tomar la raíz cuadrada. Dado que los valores de$\ x$ menos de 1 hacen que el valor dentro de la raíz cuadrada sea negativo, no habrá puntos en la gráfica de coordenadas a la izquierda de$\ x=1$. ¡No hay necesidad de elegir$\ x$ valores menores a 1 para tu mesa!
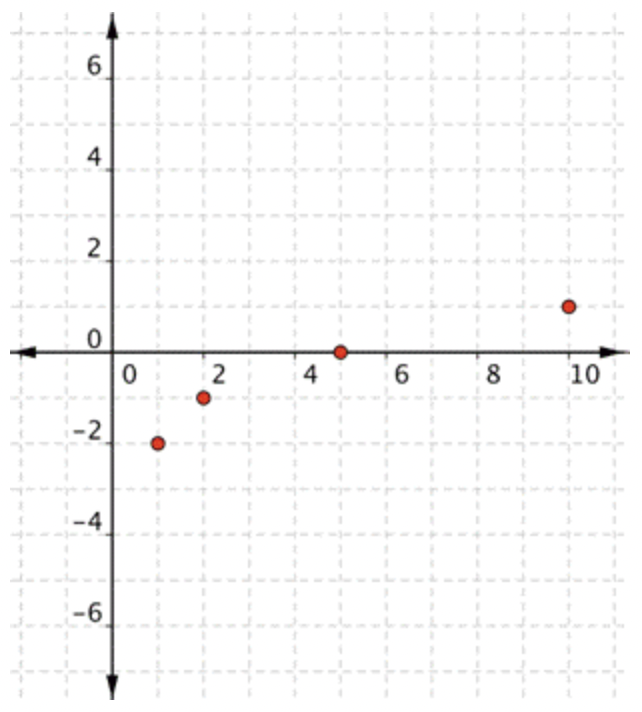$Screen Shot 2021-07-16 a las 2.27.58 PM.png$	Utilice los pares de tablas para trazar puntos.
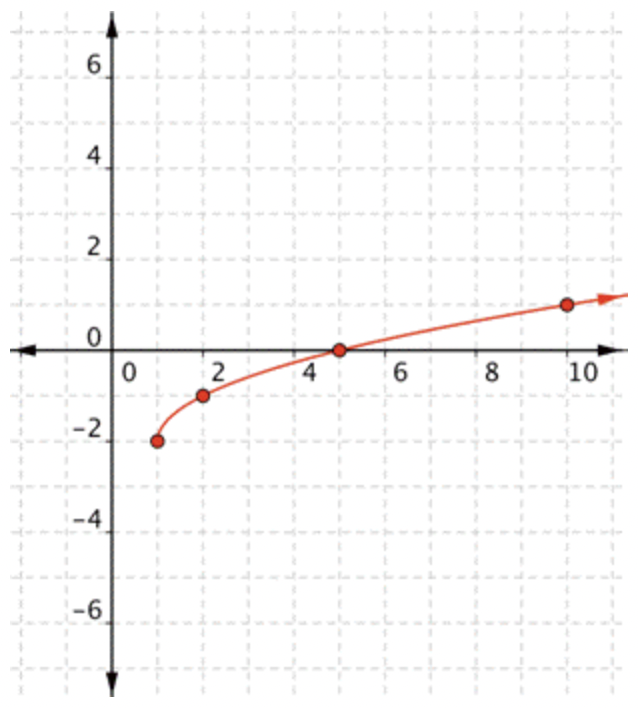$Screen Shot 2021-07-16 a las 2.29.17 PM.png$	Conecta los puntos lo mejor que puedas, usando una curva suave.

Ejercicio

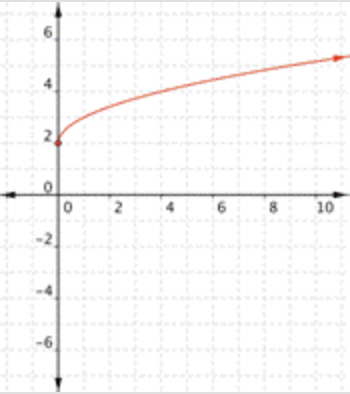
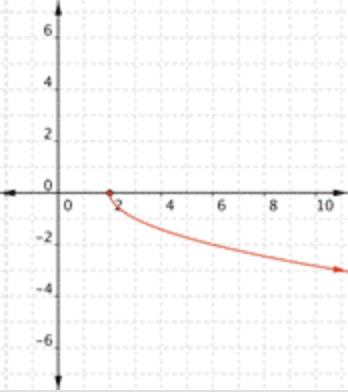
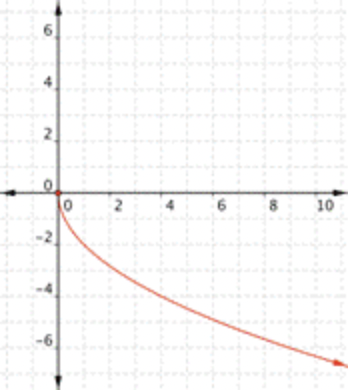
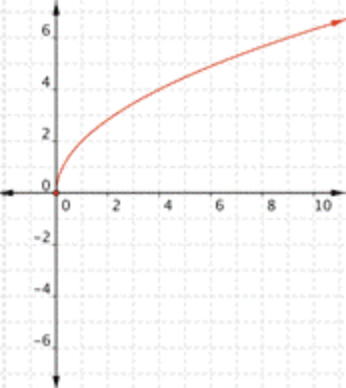
¿Cuál de las siguientes es una gráfica$\ f(x)=-2 \sqrt{x}$?

$Screen Shot 2021-07-16 a las 2.31.07 PM.png$
$Screen Shot 2021-07-16 a las 2.31.45 PM.png$
$Screen Shot 2021-07-16 en 2.32.06 PM.png$
$Screen Shot 2021-07-16 en 2.32.28 PM.png$

Contestar

Incorrecto.
Recordemos que la gráfica de$\ f(x)=-\sqrt{x}$ está completamente bajo el eje x, en el Cuadrante IV. La gráfica de$\ f(x)=-2 \sqrt{x}$ será similar pero más amplia. La respuesta correcta es Gráfica C.
Incorrecto.
En la función$\ f(x)=-2 \sqrt{x}$,$\ f(0)=0$. Este punto no está representado en esta gráfica. Encuentra una gráfica que se vea similar a la Gráfica B, pero que recorra el punto$\ (0,0)$. La respuesta correcta es Gráfica C.
Correcto.
La gráfica de$\ f(x)=-2 \sqrt{x}$ será similar a la gráfica de$\ f(x)=-\sqrt{x}$, aunque será un poco más amplia.
Incorrecto.
Esta es la gráfica de$\ f(x)=2 \sqrt{x}$. La gráfica de$\ f(x)=-2 \sqrt{x}$ estará por debajo del eje x. La respuesta correcta es Gráfica C.

Resumen

Crear una gráfica de una función es una forma de entender la relación entre las entradas y salidas de esa función. La creación de una gráfica se puede hacer eligiendo valores para$\ x$, encontrando los$\ y$ valores correspondientes y trazándolos. Sin embargo, ayuda a entender la forma básica de la función. Conocer el efecto de los cambios en la ecuación de función básica también es útil.

Una forma común que verás es una parábola. Las parábolas tienen la ecuación$\ f(x)=a x^{2}+b x+c$$\ a$, dónde$\ b$,, y$\ c$ son números reales y$\ a \neq 0$. El valor de$\ a$ determina el ancho y la dirección de la parábola, mientras que el vértice depende de los valores de$\ a$,$\ b$, y$\ c$. El vértice es$\ \left(-\frac{b}{2 a}, f\left(-\frac{b}{2 a}\right)\right)$.

\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline & \ end {array}\)	Hacer una tabla de dos columnas. Etiquetar las columnas\(\ x\) y\(\ f(x)\).
\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline-2 &\\ -1 &\\ 0 &\\ 1 &\\ 3 & \ final {matriz}\)	Elija varios valores para\(\ x\) y colóquelos como filas separadas en la\(\ x\) columna. Consejo: Siempre es bueno incluir 0, valores positivos y valores negativos, si puedes.
\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline-2 & -4\\ -1 & -1\\ 0 & 2\\ 1 & 5\\ 3 & 11 \ end {array}\)	Evalúe la función para cada valor de\(\ x\), y escriba el resultado en la\(\ f(x)\) columna junto al\(\ x\) valor que utilizó. Cuándo\(\ x=0, f(0)=3(0)+2=2\),\(\ f(1)=3(1)+2=5\),\(\ f(-1)=3(-1)+2=-3+2=-1\) y así sucesivamente.
\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline-2 & -4\\ -1 & -1\\ 0 & 2\\ 1 & 5\\ 3 & 11 \ end {array}\)	(Tenga en cuenta que su tabla de valores puede ser diferente de la de otra persona. Cada uno puede elegir diferentes números para\(\ x\).)

\(\ a=-2\), por lo que la gráfica se abrirá hacia abajo y será más delgada que\(\ f(x)=x^{2}\). \(\ c=-3\), por lo que se moverá para interceptar el eje y en\(\ (0,-3)\).	Antes de hacer una tabla de valores, mira los valores de\(\ a\) y\(\ c\) para tener una idea general de cómo debería ser la gráfica.
\ (\\ begin {array} {c\|c} x & f (x)\\ \ hline-2 & -17\\ -1 & -8\\ 0 & -3\\ 1 & -2\\ 2 & -5 \ end {array }\)	Crear una tabla de valores. Observe que en esta tabla, los\(\ x\) valores aumentan. Los\(\ y\) valores aumentan y luego comienzan a disminuir de nuevo. Eso indica una parábola.
\(\ \text { Vertex formula }=\left(\frac{-b}{2 a}, f\left(\frac{-b}{2 a}\right)\right)\) coordenada x del vértice:\(\ \frac{-b}{2 a}=\frac{-(3)}{2(-2)}=\frac{-3}{-4}=\frac{3}{4}\) coordenada y del vértice: \ (\\ begin {array} {r} f\ left (\ frac {-b} {2 a}\ right) =f\ left (\ frac {3} {4}\ right)\ f\ left (\ frac {3} {4}\ right) =-2\ left (\ frac {3} {4}\ right) ^ {2} +3\ left (\ frac {3}} {4}\ derecha) -3\\ =-2\ izquierda (\ frac {9} {16}\ derecha) +\ frac {9} {4} -3\\ =\ frac {-18} {16} +\ frac {9} {4} -3\\ =\ frac {-9} {8} +\ frac {18} {8} -\ frac {24} {8} {8}\ =-\ frac {15} {8} \ end {array}\) Vértice:\(\ \left(\frac{3}{4},-\frac{15}{8}\right)\)	Para encontrar el vértice de la parábola, usa la fórmula\(\ \left(\frac{-b}{2 a}, f\left(\frac{-b}{2 a}\right)\right)\). Encontrar el vértice puede facilitar la representación gráfica de la parábola.
$Screen Shot 2021-07-16 en 1.48.27 PM.png$	Utilice los pares de tablas para trazar puntos. Anote el vértice,\(\ \left(\frac{3}{4},-\frac{15}{8}\right)\), en azul.
$Screen Shot 2021-07-16 en 1.49.34 PM.png$	Conecta los puntos lo mejor que puedas, usando una curva suave. Recuerda que la parábola son dos imágenes especulares, así que si tus puntos no tienen pares con el mismo valor, es posible que quieras incluir puntos adicionales (como los que están en azul aquí). Trazar puntos a cada lado del vértice. \(\ x=\frac{1}{2}\)y\(\ x=\frac{3}{2}\) son buenos valores para incluir.