18.2.1: Introducción a las funciones logarítmicas

Objetivos de aprendizaje

• Convertir ecuaciones logarítmicas en ecuaciones exponenciales.
• Convertir ecuaciones exponenciales en ecuaciones logarítmicas.
• Gráfica funciones logarítmicas.
• Resolver ecuaciones logarítmicas.

Introducción

Una familia útil de funciones que se relaciona con funciones exponenciales son las funciones logarítmicas. Usted ha estado calculando el resultado de\(b^x\), y esto nos dio las funciones exponenciales. Un logaritmo es un cálculo del exponente en la ecuación\(y = b^x\). Dicho de otra manera, encontrar un logaritmo es lo mismo que encontrar el exponente al que se debe elevar la base dada para obtener el valor deseado. El exponente se convierte en la salida en lugar de la entrada.

Cálculo de exponentes

Considera estas tablas de valores utilizando una base de 2.

Tabla 1

Entrada\(x\), un exponente:\(x\)	Salida\(y\):\(y = 2^x\)
-3	\(\frac{1}{8}\)
-2	\(\frac{1}{4}\)
-1	\(\frac{1}{2}\)
0	1
1	2
2	4
3	8

Entrada\(x\), un número que es una potencia de 2:\(x = 2y\)	Salida\(y\), el exponente de 2:\(y\)
\(\frac{1}{8}\)	-3
\(\frac{1}{4}\)	-2
\(\frac{1}{2}\)	-1
1	0
2	1
4	2
8	3

Tenga en cuenta que las dos tablas son iguales excepto que las columnas se invierten: el punto (1,2) tomado de la primera tabla será el punto (2,1) en la segunda tabla.

Las gráficas de estas dos relaciones deben tener la misma forma general. Como se muestra en la gráfica, las dos curvas son simétricas alrededor de la línea\(y=x\). Otra forma de decirlo, si giras la curva roja alrededor de la línea\(y=x\), coincidirá con la curva azul. (Esto tiene sentido, porque\(y\) en la primera tabla se convierte en la segunda tabla, y viceversa).

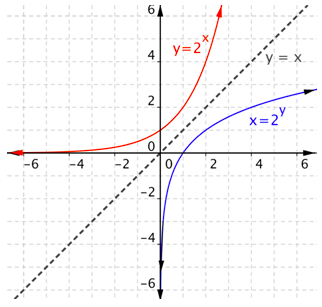
La ecuación a menudo\(x = 2^y\) se escribe como una función logarítmica (llamada función log para abreviar). La función logarítmica para\(x = 2^y\) se escribe como\(y = \log_{2} x\) o\(f(x) = \log_{2} x\). El número 2 todavía se llama la base. En general,\(y = \log_{b} x\) se lee, “\(y\)equivale a log a la base\(b\) de” \(x\), o más simplemente, “\(y\)es igual a log base\(b\) de” \(x\). Al igual que con las funciones exponenciales,\(b>0\) y\(b \neq 1\).

Se puede ver en la gráfica que el rango (\(y\)valores) de la función exponencial (en rojo) es números reales positivos. Dado que la entrada y la salida han sido conmutadas, el dominio (\(x\)valores) de la función logarítmica (en azul) son números reales positivos.

De igual manera, el dominio de la función exponencial (en rojo) es todo números reales. El rango de la función logarítmica (en azul) es todo números reales.

Definición de logaritmo

El logaritmo de\(x\) in base\(b\) está escrito\(\log _{b} x\) y se define como:

\(\log _{b} x=y\)si y sólo si\(b^{y}=x\), donde\(x>0\) y\(b>0\),\(b \neq 1\).

Conexión de ecuaciones exponenciales y logarítmicas

¡Es importante recordar que el resultado de un logaritmo es el exponente! Es decir,\(\log _{b} x\) pregunta: “¿Qué exponente en la base\(b\) dará el resultado\(x\)?”

\ (\ underbrackets {y=\ log _ {b} x} _ _ {\ begin {array} {c}
\ texto {logarítmico}
\\ texto {forma}
\ end {array}}\ texto {significa}\ underbrackets {b^ {y} =x} _ {\ begin {array} {c}
\ texto {exponencial}
\\ texto {forma}
\ final {array}\)

En ocasiones, necesitarás convertir\(\log _{b} x=y\) a\(b^{y}=x\). Otras veces, te convertirás\(b^{y}=x\) a\(\log _{b} x=y\). Los ejemplos de la tabla muestran la forma logarítmica y la forma exponencial correspondiente de varias ecuaciones.

Forma logarítmica	Forma Exponencial
\(\log _{2} 16=4\)	\(2^{4}=16\)
\(\log _{7} 1=0\)	\(7^{0}=1\)
\(\log _{5} 5=1\)	\(5^{1}=5\)
\(\log _{4} (\frac{1}{4}\)=-1	\(4^{-1}=\frac{1}{4}\)
\(\log _{10} 0.01=\log _{10} (\frac{1}{100})=-2\)	\(10^{-2}=0.01\)

Conocer esta conexión es esencial para comprender y trabajar con logaritmos.

Ejemplo

Problema: Reescribir\(\log _{3} 9=2\) como ecuación exponencial.

Contestar

Es necesario cambiar\(\log _{3} 9=2\) al formulario\(b^{y}=x\).

\(\log _{b} x=y \Leftrightarrow b^{y}=x\)

Aquí la base es 3 y el exponente es 2.

\ (\ begin {array} {lcc}
\ log _ {3} & 9 & = & 2\\
b=3 & x=9 & &y=2
\ end {array}\)

Sustituto de\(b\)\(y\),, y\(x\) en la ecuación exponencial,\(b^{y}=x\).

\(b^{y}=x \Rightarrow 3^{2}=9\)

Consulta el resultado: ¿\(3^2\)En realidad es igual a 9? ¡Sí!

\(3^{2}=9\)

Aunque la entrada de un logaritmo siempre debe ser positiva, el resultado (¡un exponente!) puede ser negativo.

Ejemplo

Problema: Convertir\(\log _{4}\left(\frac{1}{16}\right)=-2\) en una ecuación exponencial.

Contestar

Es necesario reescribir\(\log _{4}\left(\frac{1}{16}\right)=-2\) en el formulario\(b^{y}=x\).

\(\log _{b} x=y \Leftrightarrow b^{y}=x\)

Aquí la base es 4 y el exponente es -2.

\ (\ begin {array} {lcc}
\ log _ {4} &\ frac {1} {16} & =&-2\
b=4 & x=\ frac {1} {16} && y=-2
\ end {array}\)

Sustituto de\(b\)\(y\),, y\(x\) en la ecuación exponencial,\(b^{y}=x\).

\(b^{y}=x \Rightarrow 4^{-2}=\frac{1}{16}\)

Compruebe el resultado:\(4^{-2}=\left(\frac{1}{4}\right)^{2}=\frac{1}{4^{2}}=\frac{1}{16}\)

\(4^{-2}=\frac{1}{16}\)

Ejercicio

Convertir\(\log _{3}\left(\frac{1}{81}\right)=-4\) en una ecuación exponencial.

1. \(3^{4}=\frac{1}{81}\)
2. \(81^{\frac{1}{4}}=3\)
3. \(3^{-4}=\frac{1}{81}\)
4. \(3^{4}=81\)

Contestar

1. Incorrecto. El exponente es negativo, no positivo. La respuesta correcta es\(3^{-4}=\frac{1}{81}\).
2. Incorrecto. Si bien esta es una afirmación verdadera, la base en esta respuesta es 81, mientras que la base en la ecuación logarítmica original es 3. La respuesta correcta es\(3^{-4}=\frac{1}{81}\).
3. Correcto. La base es 3 y el exponente es -4, entonces\(3^{-4}=\frac{1}{81}\).
4. Incorrecto. Si bien esta es una afirmación verdadera, el exponente en la ecuación logarítmica original es -4, no 4. La respuesta correcta es\(3^{-4}=\frac{1}{81}\).

Como acabas de ver, es posible convertir ecuaciones logarítmicas en ecuaciones exponenciales. También es posible convertir la ecuación exponencial en ecuaciones logarítmicas.

Ejemplo

Problema: Reescribir\(5^{3}=125\) como una ecuación logarítmica.

Contestar

Necesitas reescribir\(5^{3}=125\) en el formulario _{\(\log _{b} x=y\)}.

\(b^{y}=x \Leftrightarrow \log _{b} x=y\)

Aquí la base es 5 y el exponente es 3.

\(5^{3}=125\)

Sustituir por\(b\),\(y\), y\(x\) en la ecuación logarítmica,\(\log _{b} x=y\).

\(\log _{b} x=y \Rightarrow \log _{5} 125=3\)

\(\log _{b} 125=3\)

Ejemplo

Problema: Convertir\(10^{-3}=\frac{1}{1,000}\) en una ecuación logarítmica.

Contestar

Es necesario reescribir\(10^{-3}=\frac{1}{1,000}\) en el formulario\(\log _{b} x=y\).

\(b^{y}=x \Leftrightarrow \log _{b} x=y\)

Aquí la base es 10 y el exponente es -3.

\ (
10^ {-3} =\ frac {1} {1,000}\
\ text {Donde} b=10^ {-3}\ texto {y} y=-3\ texto {y}\\
x=\ frac {1} {1,000}
\)

Sustituir por\(b\),\(y\), y\(x\) en la ecuación logarítmica,\(\log _{b} x=y\).

\(\log _{b} x=y \Rightarrow \log _{10}\left(\frac{1}{1,000}\right)=-3\)

\(\log _{10} \frac{1}{1,000}=-3\)

Recuerda que las raíces también son exponentes.

Ejemplo

Problema: Convertir\(\sqrt{49}=7\) en una ecuación logarítmica.

Contestar

Reescribe la raíz cuadrada usando un exponente fraccionario. Es necesario reescribir\(49^{\frac{1}{2}}=7\) en el formulario\(\log _{b} x=y\).

\(\sqrt{49}=49^{\frac{1}{2}}\)

\ (\ begin {array} {c}
b^ {y} =x\ Leftrightarrow\ log _ {b} x=y\\
49^ {\ frac {1} {2}} =7
\ end {array}\)

Aquí, la base es 49 y el exponente lo es\(\frac{1}{2}\).

Dónde\(b=49\) y\(y=\left(\frac{1}{2}\right)\) y\(x = 7\)

Sustituir por\(b\),\(y\), y\(x\) en la ecuación logarítmica,\(\log _{b} x=y\).

\(\log _{49} 7=\frac{1}{2}\)

Ejercicio

Convertir\(11^{2}=121\) en una ecuación logarítmica.

1. \(\log _{11} 2=121\)
2. \(\log _{121} 11=2\)
3. \(\log _{11} 121=2\)
4. \(\log _{121} 2=11\)

Contestar

1. Incorrecto. Encontrar un logaritmo es lo mismo que encontrar el exponente al que se debe elevar la base dada para obtener el valor deseado, por lo que 2 debe estar por sí mismo en un lado de la ecuación. La respuesta correcta es\(\log _{11} 121=2\).
2. Incorrecto. La base de la ecuación exponencial, 11, es también la base (el pequeño número de subíndice al final de “log”) en la ecuación logarítmica. La respuesta correcta es\(\log _{11} 121=2\).
3. Correcto. La base es 11, y el resultado del logaritmo, 2, es el exponente.
4. Incorrecto. La base de la ecuación exponencial, 11, es también la base (el pequeño número de subíndice al final de “log”) en la ecuación logarítmica. La respuesta correcta es\(\log _{11} 121=2\).

Graficar funciones logarítmicas

Mira la gráfica a continuación. Debería parecer familiar: ¡lo viste antes en este tema! El gráfico azul es la función logarítmica, y el gráfico rojo es la función exponencial correspondiente.

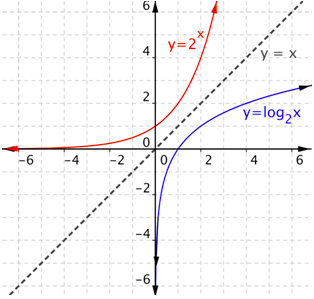
Al graficar funciones logarítmicas, es importante recordar lo siguiente:

• La gráfica sólo puede aparecer a la derecha del\(y\) eje -axis. Esto se debe a que el dominio está restringido a valores positivos de\(x\).
• La gráfica se acerca al\(y\) eje -para valores pequeños de\(x\) (cerca de\(x=0\)).

Recuerde que las funciones logarítmicas casi actúan como funciones exponenciales. Sólo hay que cambiar los\(y\) valores\(x\) y. Por ejemplo, el segundo elemento con viñetas anterior es como la función exponencial que se acerca al\(x\) eje -( cerca de\(y=0\)).

Ejemplo

Problema: Gráfica\(f(x)=\log _{3} x\).

Contestar

Para facilitar los cálculos, primero haga de esta una ecuación logarítmica en\(y\). Después convierte el logaritmo en una ecuación exponencial.

Gráfica\(y=\log _{3} x\). Esto es lo mismo que\(3^{y}=x\).

Comience con una tabla de valores. Con funciones logarítmicas, suele ser más fácil elegir los\(y\) valores en lugar de los\(x\) valores. Asegúrese de incluir algunos valores negativos para\(y\).

\(x = 3^y\)	\(y\)
	-2
	-1
	0
	1
	2

¡Cuidado con los exponentes negativos!

\(x = 3^y\)	\(y\)
\(\frac{1}{9}\)	-2
\(\frac{1}{3}\)	-1
1	0
3	1
9	2

Utilice la tabla como pares ordenados. Recuerde que la gráfica de la función mostrará todas las\(x - y\) correspondencias, por lo que cualquier par que pudiera estar en la tabla debe estar en la gráfica.

Trazar los puntos.

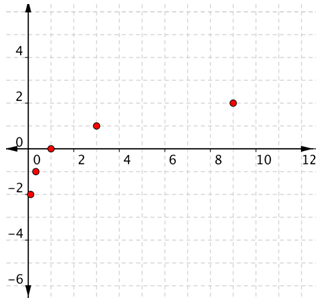
Como los puntos no están en una línea, no se puede usar una recta. Conecta los puntos lo mejor que puedas, usando una curva suave (no una serie de líneas rectas).

Recuerda que las funciones logarítmicas se acercan al\(y\) eje -( pero no lo tocarán ni cruzarán).

Ejemplo

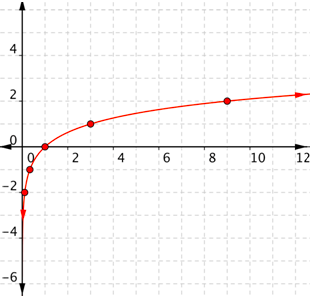
Problema: Gráfica\(f(x)=\log _{4} x\).

Contestar

Para facilitar los cálculos, primero haga de esta una ecuación logarítmica en\(y\). Después convierte el logaritmo en una ecuación exponencial.

Gráfica\(y=\log _{4} x\). Esto es lo mismo que\(4^y = x\).

Comience con una tabla de valores, eligiendo los\(y\) valores y calculando\(x\). ¡Cuidado con los exponentes negativos!

\(x = 4^y\)	\(y\)
\(\frac{1}{16}\)	-2
\(\frac{1}{4}\)	-1
1	0
4	1
16	2

Usa la tabla como pares ordenados y traza los puntos.

En este caso, (16, 2) no se mostrará en la gráfica. Porque conoces la raíz cuadrada de 4, inténtalo\(x = \frac{3}{2}\). En este caso, lo sería\(4^{\frac{3}{2}}=(\sqrt{4})^{3}=2^{3}=8\). Ese punto se muestra en azul.

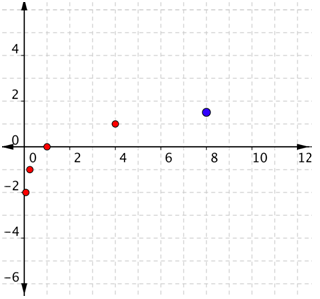
Como los puntos no están en una línea, no se puede usar una recta. Conecta los puntos lo mejor que puedas, usando una curva suave (no una serie de líneas rectas).

Recuerda que las funciones logarítmicas se acercan al\(y\) eje -( pero no lo tocarán ni cruzarán).

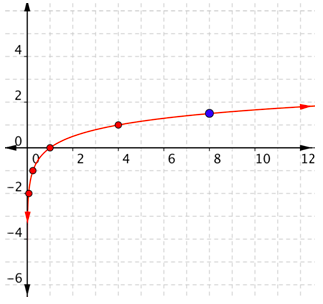
Comparemos las gráficas logarítmicas que has visto:\(f(x)=\log _{2} x\),\(f(x)=\log _{3} x\), y\(f(x)=\log _{4} x\).

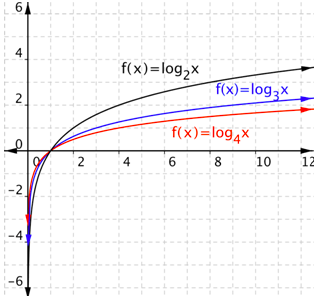
Observe que una base más grande hace que la gráfica sea menos empinada. (Esto es lo opuesto a las funciones exponenciales, donde una base más grande significaba una gráfica más pronunciada). Una base más grande también hace que la gráfica esté más cerca\(x\) del eje -para\(y > 0\) (o\(x > 1\)) y más cerca del\(y\) eje -para\(y < 0\) (o\(x < 1\)). Todas las gráficas pasan por (1, 0), mientras que las funciones exponenciales siempre pasan por (0, 1).

Con funciones exponenciales, las gráficas fueron crecientes (crecimiento exponencial) cuando la base\(b\) fue mayor a 1. Las gráficas fueron decrecientes (decaimiento exponencial) cuando la base\(b\) era menor a 1. Las gráficas logarítmicas anteriores son todas crecientes, y todas tienen una base mayor a 1. Veamos qué pasa con una base menor a 1.

Ejemplo

Problema: Gráfica\(f(x)=\log _{\frac{1}{4}} x\).

Contestar

Escribe una ecuación exponencial\(y\) para ayudarte.

\ (\ begin {array} {l}
y=\ log _ {\ frac {1} {4}} x\\
\ izquierda (\ frac {1} {4}\ derecha) ^ {y} =x
\ end {array}\)

Crear una tabla de valores. Nuevamente, recuerda tener cuidado con los exponentes negativos. Recuerda tomar el recíproco de la base para hacer positivo al exponente. \(\left(\frac{1}{4}\right)^{-2}=\left(\frac{4}{1}\right)^{2}=4^{2}=16\)

\(x\)	\(y\)
16	-2
4	-1
1	0
\(\frac{1}{4}\)	1
\(\frac{1}{16}\)	2

Observe que en esta tabla, los\(x\) valores disminuyen a medida que aumentan los\(y\) valores.

Utilice los pares de tablas para trazar puntos. Es posible que desee incluir nuevos puntos, especialmente cuando uno de los puntos de la tabla no cabe en su gráfica. (16, -2) está fuera de la gráfica. Porque conoces la raíz cuadrada de 4, prueba\(x = -\frac{3}{2}\):\(\left(\frac{1}{4}\right)^{-\frac{3}{2}}=\left(\frac{4}{1}\right)^{\frac{3}{2}}=4^{\frac{3}{2}}=(\sqrt{4})^{3}=2^{3}=8\)

El punto (8, -\(\frac{3}{2}\)) ha sido incluido en azul. Es posible que no sienta necesario incluir puntos adicionales. También es posible que necesites usar una calculadora, dependiendo de la base.

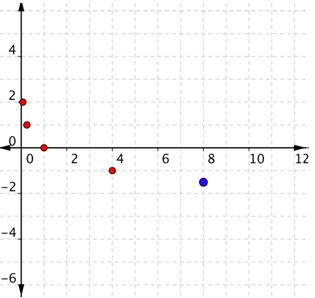
Conecta los puntos lo mejor que puedas, usando una curva suave.

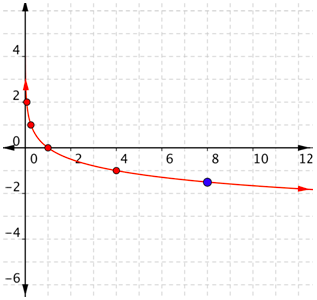
Si la base es menor que 1, la función logarítmica es decreciente. La gráfica se acerca al\(y\) eje -cuando\(x\) es pequeña, pero con\(y\) valores positivos en lugar de negativos.

Ejercicio

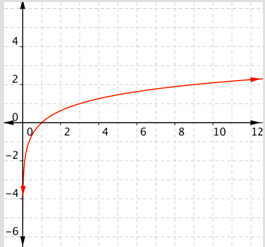
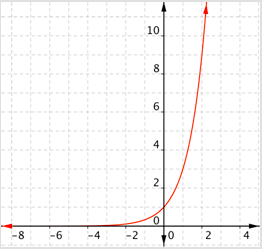
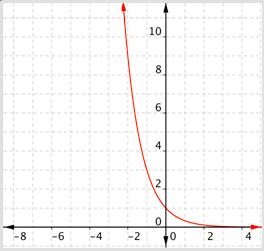
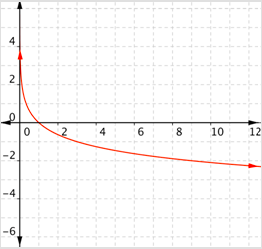
¿Cuál de las siguientes es una gráfica\(f(x)=\log _{\frac{1}{3}} x\)?

1. 
2. 
3. 
4. 

Contestar

1. Incorrecto. Esta gráfica va en aumento debido a que los\(f(x)\) valores van aumentando a medida que\(x\) aumenta. (Compare los valores para\(x = 1\) y\(x = 2\).) Esta es una gráfica de\(f(x)=\log _{3} x\). La respuesta correcta es Gráfica D.
2. Incorrecto. Esta función tiene un dominio de todos los números reales y un rango de números reales positivos. Las funciones logarítmicas tienen dominios de números reales positivos y rangos de todos los números reales. La respuesta correcta es Gráfica D.
3. Incorrecto. Esta gráfica es decreciente, pero tiene un dominio de todos los números reales y un rango de números reales positivos. Las funciones logarítmicas tienen dominios de números reales positivos y rangos de todos los números reales. La respuesta correcta es Gráfica D.
4. Correcto. La base es menor que 1, por lo que la gráfica muestra una función decreciente. El dominio son números reales positivos, y el rango es todo números reales.

Resolver ecuaciones logarítmicas

Como has visto, hay tres cantidades esenciales en una ecuación logarítmica\(y=\log _{b} x\): la base\(b\), el exponente\(y\) y la entrada\(x\). Cualquiera de estos podría faltar en una ecuación que necesites resolver. A menudo, la forma más fácil de resolverlos es convertir la ecuación logarítmica en una ecuación exponencial.

Ejemplo

Problema: Resolver\(4=\log _{5} x\).

Contestar

Convierta la ecuación logarítmica en una ecuación exponencial.

\(4=\log _{5} x \text { means } 5^{4}=x\)

En este caso, solo necesitas evaluar\(5^4\) para resolver\(x\).

\ (\ begin {array} {c}
5^ {4} =5\ cdot 5\ cdot 5\ cdot 5\ cdot 5\\
5^ {4} =25\ cdot 25\
5^ {4} =625
\ end {array}\)

\(x=625\)

Al resolver por\(b\) o\(y\), es útil conocer muchas relaciones exponenciales, como\(5^3 = 125\) y\(2^5 = 32\), de la parte superior de tu cabeza. Sin embargo, aunque no lo hagas, puedes pensar un poco para aproximar, o incluso encontrar exactamente, las soluciones.

Ejemplo

Problema: Resolver\(3=\log _{b} 64\).

Contestar

Convierta la ecuación logarítmica en una ecuación exponencial.

\(3=\log _{b} 64 \text { means } b^{3}=64\)

Quizá no sepas qué número a la tercera potencia es 64. Sin embargo, puedes probar algunos y ponértelo rápidamente. \(1^3\)y\(10^3\) son fáciles de calcular, así que empecemos por ahí.

\ (\ begin {array} {c}
1^ {3} =1\\
10^ {3} =1,000
\ end {array}\)

64 está mucho más cerca de 1 que de 1,000, por lo que la base correcta estará más cerca de 1 que de 10.

Probemos algunos otros valores bajos. Ya que 64 es par, sabes que no necesitas probar ningún número impar. Un número impar a cualquier potencia siempre será impar, y un número par para cualquier potencia siempre será par.

Entonces probemos 2 y 4.

\ (\ begin {array} {c}
2^ {3} =8\\
4^ {3} =4\ cdot 16=64
\ end {array}\)

¡Lo encontré! Asegúrese de proporcionar el número correcto para su respuesta. ¡Sería fácil responder erróneamente al “64” aquí!

\(b=4\)

Vamos a probar uno más:

Ejemplo

Problema: Resolver\(y=\log _{5} 125\).

Contestar

Convierta la ecuación logarítmica en una ecuación exponencial.

\(y=\log _{5} 125 \text { means } 5^{y}=125\)

¿Qué potencia de 5 es 125? Puede que sepas, pero si no lo haces, haz una tabla de valores para\(y\) y\(5^y\). Busque 125, o cerca de él, en la\(5^y\) columna.

\(y\)	\(5^y\)
1	5
2	25
3	125

Nuevamente, asegúrese de proporcionar el número correcto. ¡Sería fácil equivocarse y escribir 125 aquí!

\(y = 3\)

Ejercicio

Resolver\(4=\log _{2} x\) para\(x\).

1. \(\frac{1}{2}\)
2. 2
3. 8
4. 16

Contestar

1. \(\frac{1}{2}\). Incorrecto. La ecuación exponencial equivalente es\(2^4 = x\). Es posible que hayas escrito incorrectamente\(4^x = 2\). La respuesta correcta es 16.
2. 2. Incorrecto. La ecuación exponencial equivalente es\(2^4 = x\). Es posible que hayas escrito incorrectamente\(2^x = 4\). La respuesta correcta es 16.
3. 8. Incorrecto. La ecuación exponencial equivalente es\(2^4 = x\). La respuesta correcta es 16.
4. 16. Correcto. La ecuación exponencial equivalente es\(2^4 = x\), que es 16.

Resumen

Las funciones logarítmicas están estrechamente relacionadas con las ecuaciones exponenciales. De hecho,\(\log _{b} x=y\) dice lo mismo que\(b^{y}=x\). Las gráficas se ven similares, pero con características como el dominio y el rango cambiados entre los\(x\) valores y los\(y\) valores. Convertir una ecuación logarítmica a la ecuación exponencial equivalente es útil tanto para graficar como para resolver ecuaciones.