19.1.1: Identificación de las Seis Funciones Trigonométricas

Objetivos de aprendizaje

• Identificar la hipotenusa, lado adyacente y lado opuesto de un ángulo agudo en un triángulo rectángulo.
• Determinar las seis relaciones trigonométricas para un ángulo dado en un triángulo rectángulo.
• Reconocer la relación recíproca entre seno/cosecante, coseno/secante y tangente/cotangente.
• Utilice una calculadora para encontrar el valor de las seis funciones trigonométricas para cualquier ángulo agudo.
• Usa una calculadora para encontrar la medida de un ángulo dado el valor de una función trigonométrica.

Introducción

Supongamos que desea construir una rampa para acceder a un muelle de carga que se encuentra a 4 pies sobre el nivel del suelo. Quieres poder empujar fácilmente un carro sobre ruedas por la rampa, y el ángulo de elevación no debe ser mayor de 20\(^{\circ}\). ¿Cuánto tiempo tiene que durar la rampa?

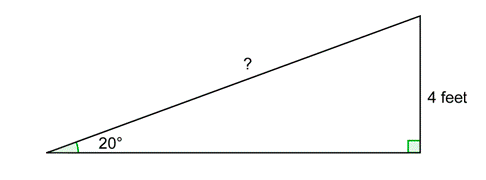
En este diagrama, tienes un triángulo rectángulo para el que conoces la longitud de un lado y la medida de un ángulo agudo. Se quiere encontrar la longitud de la hipotenusa. Quizás sepas que el Teorema de Pitágoras te permite encontrar la longitud de un lado de un triángulo rectángulo, dadas las longitudes de los otros dos lados. Ahora aprenderás trigonometría, que es una rama de las matemáticas que estudia la relación entre los ángulos y los lados de los triángulos. De hecho, la trigonometría te permitirá encontrar longitudes de lado y medidas de ángulo desconocidas en triángulos rectos en una variedad de casos, como en el problema anterior.

Los lados de un triángulo rectángulo

En el ejemplo anterior, uno de los ángulos agudos tiene una medida de 20\(^{\circ}\). Podrías describir el lado (o pierna del triángulo rectángulo) con longitud 4 pies como la altura del triángulo, o podrías decir que es “opuesto” al\(^{\circ}\) ángulo de 20. Se dice que la otra pata es “adyacente” al\(^{\circ}\) ángulo 20. En la trigonometría, este tipo de relación entre lados y ángulos es muy importante.

La relación general entre lados y ángulos se muestra en el siguiente diagrama.

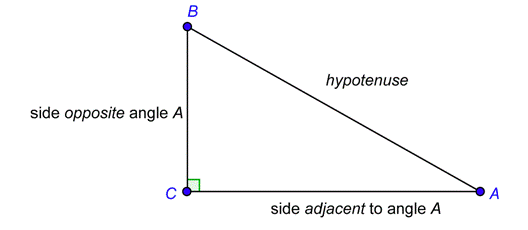
\(A\)El ángulo está formado por la hipotenusa y la pierna\(\overline{CA}\). Decimos que la pierna\(\overline{CA}\) es el lado adyacente al ángulo\(A\). Decimos que la pierna\(\overline{BC}\) es el lado opuesto al ángulo\(A\). Es decir, el lado adyacente es la pata que forma parte del ángulo; el lado opuesto es la pata que no forma parte del ángulo.

Ejemplo

Problema: ¿Cuál es la longitud del lado opuesto al ángulo\(X\) y la longitud del lado adyacente al ángulo\(X\)?

Contestar

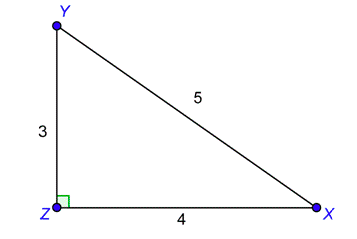
El lado opuesto al ángulo\(X\) es\(\overline{YZ}\). Su longitud es de 3. El lado adyacente al ángulo\(X\) es\(\overline{ZX}\). Su longitud es de 4.

Largo lado opuesto: 3

longitud del lado adyacente: 4

Ten en cuenta que las etiquetas “opuestas” y “adyacentes” dependen del ángulo del que estés hablando. El lado opuesto a un ángulo no necesita ser la altura del triángulo. Considera el siguiente ejemplo:

Ejemplo

Problema: ¿Cuál es el nombre del lado opuesto al\(^{\circ}\) ángulo 40 y el nombre del lado adyacente al\(^{\circ}\) ángulo 40?

Contestar

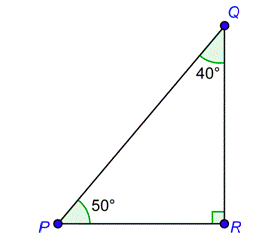
El\(^{\circ}\) ángulo 40 está formado por la hipotenusa y\(\overline{QR}\), así lo\(\overline{QR}\) está el lado adyacente. Ya\(\overline{PR}\) que no forma parte del\(^{\circ}\) ángulo 40, es el lado opuesto.

lado opuesto:\(\overline{PR}\)

lado adyacente:\(\overline{QR}\)

Cada pata en un triángulo rectángulo es adyacente a uno de los ángulos agudos y opuesta al otro ángulo agudo.

Ejemplo

Problema: En\(\bigtriangleup AB\),\(\overline{DA}\) ¿lado está adyacente a qué ángulo y opuesto a qué ángulo?

Contestar

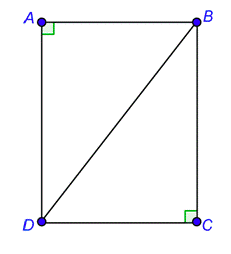
Lado\(\overline{DA}\) y la hipotenusa\(\overline{DB}\) se forman juntos\(\angle ADB\). Así\(\overline{DA}\) es adyacente a\(\angle ADB\). Ya\(\overline{DA}\) que no forma parte del ángulo agudo\(\angle ABD\),\(\overline{DA}\) es el lado opuesto\(\angle ABD\).

adyacente a\(\angle ADB\)

opuesto\(\angle ABD\)

Las seis relaciones trigonométricas

Supongamos que su profesor le pide a usted y a otro alumno que dibujen un triángulo con medidas de ángulo 35\(^{\circ}\)\(^{\circ}\), 55 y 90\(^{\circ}\). Usted y su amigo probablemente dibujarán triángulos de diferentes tamaños. No obstante, debido a que los triángulos tendrán las mismas medidas de ángulo, serán similares.

Recuerda que esto significa que los triángulos tendrán lados proporcionales correspondientes. Por ejemplo, un triángulo podría tener lados que son todos dos veces más largos que los lados del otro, como se ve a continuación.

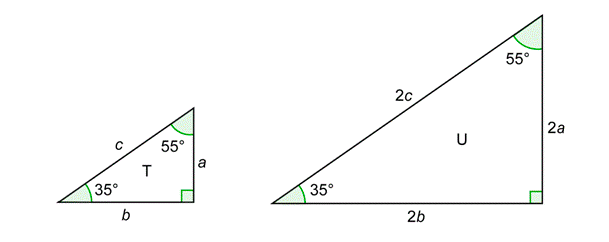
Ahora supongamos que a cada uno de ustedes se le ha pedido encontrar la relación del lado opuesto al\(^{\circ}\) ángulo 35 sobre la hipotenusa. Aunque estés usando diferentes triángulos y tendrás diferentes números en el numerador y denominador, seguirás acabando con el mismo resultado. Ustedes dos obtendrán:

\(\dfrac{\text { opposite } 35^{\circ} \text { in } \mathrm{T}}{\text { hypotenuse of } \mathrm{T}}=\dfrac{a}{c} \text { and } \dfrac{\text { opposite } 35^{\circ} \text { in } \mathrm{U}}{\text { hypotenuse of } \mathrm{U}}=\dfrac{2 a}{2 c}=\dfrac{a}{c}\)

Los dos ratios son los mismos porque los 2s cancelan. Si dibujas un triángulo con los mismos ángulos y lados que son tres veces más largos que los del triángulo T, la relación del lado opuesto 35\(^{\circ}\) sobre la hipotenusa será\(\frac{3a}{3c} = \frac{a}{c}\). Esta relación será la misma para todos los triángulos similares, y esta relación se denomina seno de 35\(^{\circ}\). Seno se abrevia como\(\sin {35^{\circ}}\).

El mismo tipo de resultado ocurrirá si usas otras proporciones de lados. Por ejemplo, si tomas la proporción del lado adyacente a 35\(^{\circ}\) sobre la hipotenusa, obtendrás\(\frac{b}{c}\) sin importar cuál de los triángulos anteriores uses.

Además de la relación sinusoidal, hay otras cinco proporciones que puedes calcular: cos, tan, cot, sec y csc. Así como el pecado es una abreviatura de seno, cos es la abreviatura de coseno, el bronceado es la abreviatura de tangente, csc es la abreviatura de cosecante, sec es la abreviatura de secante y cot es la abreviatura de cotangente. (Al leer estas abreviaturas en voz alta, es necesario decir la palabra completa). Estas seis proporciones te ayudarán a encontrar longitudes de lado desconocidas y medidas de ángulo desconocidas en triángulos rectos. Veamos las definiciones para estas seis proporciones, comenzando con un triángulo rectángulo típico como el de abajo.

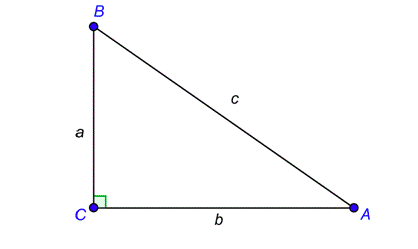
Las definiciones son las siguientes:

\ (\ begin {array} {cc}
\ sin A=\ dfrac {\ text {opuesto}} {\ texto {hipotenusa}} =\ dfrac {a} {c} &\ csc A=\ dfrac {\ texto {hipotenusa}} {\ texto {opuesto}} =\ dfrac {c} {a}\\ cos A=\ dfrac {
\ texto {\ texto {\ texto {\ texto {opuesto}} adyacente}} {\ texto {hipotenusa}} =\ dfrac {b} {c} &\ seg A=\ dfrac {\ texto {hipotenusa}} {\ texto {adyacente}} =\ dfrac {c} {b}\
\ tan A=\ dfrac {\ texto {opuesto}} {\ texto {adyacente}} =\ dfrac {a} {b} &\ cot A=\ dfrac {\ texto {adyacente}} {\ texto {opuesto}} =\ dfrac {b} {a}
\ end {array}\)

Dadas estas definiciones, practiquemos aplicándolas.

Ejemplo

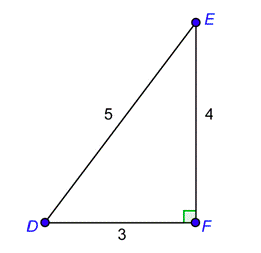
Problema: Determinar las seis relaciones trigonométricas para el ángulo\(D\) en el triángulo rectángulo abajo.

RESPUESTAS

Lo primero que hay que hacer es reconocer que\(\overline{EF}\) es ángulo opuesto\(D\) y\(\overline{DF}\) es adyacente al ángulo\(D\). Después anote sus longitudes.

longitud del lado opuesto\(D\) = 4

longitud del lado adyacente a\(D\) = 3

longitud de la hipotenusa = 5

Sustituir estos valores en las definiciones para las seis proporciones.

\ (\ begin {array} {c}
\ sin D=\ frac {\ text {opuesto}} {\ texto {hipotenusa}} =\ frac {4} {5}
\\ cos D=\ frac {\ texto {adyacente}} {\ texto {hipotenusa}} =\ frac {3} {5}
\\ tan D=\ frac {\ texto {opuesto}} {texto {adyacente}} =\ frac {4} {3}\
\ csc D=\ frac {\ texto { hipotenusa}} {\ texto {opuesto}} =\ frac {5} {4}\
\ seg D=\ frac {\ texto {hipotenusa}} {\ texto {adyacente}} =\ frac {5} {3}\
\ cuna D=\ frac {\ texto {adyacente}} {\ texto {opuesto}} =\ frac {3} {4}
\ end {array}\)

\(\sin D = \frac{4}{5}\),\(\cos D = \frac{3}{5}\),\(\tan D = \frac{4}{3}\)

\(\csc D = \frac{5}{4}\),\(\sec D = \frac{5}{3}\),\(\cot D = \frac{3}{4}\)

Observe que los valores de seno y coseno están entre 0 y 1. Los encontraste dividiendo la longitud de una pierna por la hipotenusa. La hipotenusa es el lado más largo, por lo que el numerador es menor que el denominador. Eso significa que la salida de la función seno o coseno es siempre menor que 1.

Tenga en cuenta que el lado opuesto para un ángulo agudo es el lado adyacente del otro ángulo agudo. En el ejemplo anterior, lado\(EF\) era el lado opuesto para ángulo\(D\). Pero, como verás en el siguiente ejemplo, será el lado adyacente para ángulo\(E\).

Ejemplo

Problema: Determinar las seis relaciones trigonométricas para el ángulo en el triángulo rectángulo abajo.

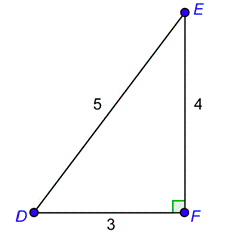
Contestar

Este es el mismo triángulo que viste en el ejemplo anterior, por lo que la hipotenusa es la misma. La diferencia es que estás mirando el triángulo desde la perspectiva de ángulo\(E\) en lugar de ángulo\(D\). Entonces los lados opuestos y adyacentes cambian de lugar. Es decir,\(\overline{EF}\) es adyacente al ángulo\(E\) y\(\overline{DF}\) es opuesto al ángulo\(E\).

longitud del lado opuesto\(E\) = 3

longitud del lado adyacente a\(E\) = 4

longitud de la hipotenusa = 5

Sustituir los nuevos valores en las definiciones para las seis proporciones.

\ (\ begin {array} {c}
\ sin E=\ frac {\ text {opuesto}} {\ texto {hipotenusa}} =\ frac {3} {5}
\\ cos E=\ frac {\ texto {adyacente}} {\ texto {hipotenusa}} =\ frac {4} {5}
\\ tan E=\ frac {\ texto {opuesto}} {texto {adyacente}} =\ frac {3} {4}\
\ csc E=\ frac {\ texto { hipotenusa}} {\ texto {opuesto}} =\ frac {5} {3}\
\ seg E=\ frac {\ texto {hipotenusa}} {\ texto {adyacente}} =\ frac {5} {4}\
\ cuna E=\ frac {\ texto {adyacente}} {\ texto {opuesto}} =\ frac {4} {3}
\ end {array}\)

\(\sin E = \frac{3}{5}\),\(\cos E = \frac{4}{5}\),\(\tan E = \frac{3}{4}\)

\(\csc E = \frac{5}{3}\),\(\sec E = \frac{5}{4}\),\(\cot E = \frac{4}{3}\)

Si comparas las respuestas con los dos últimos ejemplos, verás lo siguiente:

\(\sin D = \frac{4}{5} = \cos E\)

Estas dos funciones trigonométricas son iguales porque el lado opuesto al ángulo\(D\) (que es 4) es el lado adyacente al ángulo\(E\). Porque son los dos ángulos agudos en un triángulo rectángulo,\(D\) y\(E\) son complementarios. Es decir:

\(D + E = 90^{\circ}\)

o

\(E = 90^{\circ} - D\)

Sustituya esto en la ecuación anterior:

\(\sin D = \cos (90^{\circ} - D)\)

Nuevamente, la razón por la que estas dos funciones son iguales es que el lado opuesto a un ángulo agudo es el lado adyacente al otro ángulo agudo. Esto es cierto en cualquier triángulo rectángulo. Entonces, si\(A\) hay algún ángulo agudo, siempre es cierto que:

\(\sin A = \cos (90^{\circ} - A)\)

Comparando más respuestas de los dos últimos ejemplos, puedes encontrar estas relaciones:

\(\sec D = \frac{5}{3} = \csc E and \tan D = \frac{4}{3} = \cot E\)

Obtienes estas igualdades porque (1) el lado adyacente al ángulo\(D\) es 3, mientras que este es el lado opuesto al ángulo\(E\), y (2) el lado opuesto al ángulo\(D\) es 4, mientras que este es el lado adyacente al ángulo\(E\). Estos son ejemplos de la relación general que hemos expuesto: el lado opuesto a un ángulo agudo es el lado adyacente al otro ángulo agudo. Usando el mismo razonamiento anterior, si\(A\) hay algún ángulo agudo, siempre es cierto que:

\ (\ begin {array} {l}
\ sin A=\ cos\ izquierda (90^ {\ circ} -A\ derecha)\\
\ seg A=\ csc\ izquierda (90^ {\ circ} -A\ derecha)\\
\ tan A=\ cot\ izquierda (90^ {\ circ} -A\ derecha)
\ end {array}\)

Una ecuación, como cualquiera de las tres anteriores, que es cierta para cualquier valor de la variable se denomina identidad. Anote los nombres completos de estas funciones: seno y coseno, secante y cosecante, tangente y cotangente. Estos pares se conocen como cofunciones. Los ángulos\(A\) y\(90^{\circ} - A\) son complementarios. En otras palabras, las cofunciones de cualquier par de ángulos complementarios son iguales.

Puede utilizar estas relaciones para encontrar valores de funciones trigonométricas a partir de valores de otras funciones sin dibujar un triángulo. Tenga en cuenta que puede reemplazar\(A\) y\(90^{\circ} - A\) por\(B\) y\(90^{\circ} - B\). La letra diferente no va a cambiar la relación, porque estos ángulos siguen siendo complementarios.

Ejemplo

Problema: Un triángulo rectángulo tiene ángulos agudos\(A\) y\(B\). Si\(\sin A = \frac{7}{25}\) y\(\tan B = \frac{24}{7}\), ¿qué son\(\cos B\) y\(\cot A\)?

Contestar

Dado que\(A\) y\(B\) son los ángulos agudos en un triángulo rectángulo, son ángulos complementarios.

\ (\ begin {array} {c}
A+B=90^ {\ circ}\\
\ text {o}\\
B=90^ {\ circ} -A\\
\ text {o}\\
A=90^ {\ circ} -B
\ end {array}\)

Sustituto de\(B\). Usa la identidad (las cofunciones son iguales). Sustituir el valor dado.

\ (\ begin {array} {c}
\ cos B=\ cos\ left (90^ {\ circ} -A\ derecha)\\
=\ sin A\\
=\ frac {7} {25}
\ end {array}\)

Sustituto de\(A\). Las cofunciones de cualquier par de ángulos complementarios son iguales. Sustituir el valor dado.

\ (\ begin {array} {c}
\ cot A=\ cot\ left (90^ {\ circ} -B\ derecha)\\
=\ tan B\\
=\ frac {24} {7}
\ end {array}\)

\ (\ cos B =\ frac {7} {25},\ cuna A =\ frac {24} {7}

Ejercicio

¿Cuáles son los valores de\(\cos U\) y\(\csc U\)?

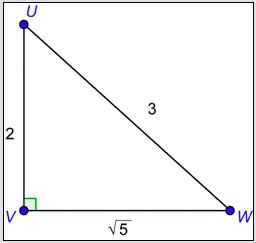
1. \(\cos U=\frac{\sqrt{5}}{3} \text { and } \csc U=\frac{3}{2}\)
2. \(\cos U=\frac{3}{2} \text { and } \csc U=\frac{\sqrt{5}}{3}\)
3. \(\cos U=\frac{2}{3} \text { and } \csc U=\frac{3}{\sqrt{5}}\)
4. \(\cos U=\frac{3}{\sqrt{5}} \text { and } \csc U=\frac{2}{3}\)

Contestar

1. \(\cos U=\frac{\sqrt{5}}{3} \text { and } \csc U=\frac{3}{2}\). Incorrecto. Probablemente usaste el ángulo agudo\(W\), y encontraste\(\cos W\) y\(\csc W\). Recuerda que obtienes diferentes proporciones para los dos ángulos agudos, así que presta mucha atención a qué ángulo estás usando. La respuesta correcta es C.
2. \(\cos U=\frac{3}{2} \text { and } \csc U=\frac{\sqrt{5}}{3}\). Incorrecto. Es posible que hayas usado el ángulo agudo\(W\) y también cambiaste coseno y cosecante. Recuerda que obtienes diferentes proporciones para los dos ángulos agudos, así que presta mucha atención a qué ángulo estás usando. La respuesta correcta es C.
3. \(\cos U=\frac{2}{3} \text { and } \csc U=\frac{3}{\sqrt{5}}\). Correcto. Usando la definición de coseno,\(\cos U = \frac{\text { adjacent }}{\text { hypotenuse }} = \frac{2}{3}\). Utilizando la definición de cosecante,\(\csc U = \frac{\text { hypotenuse }}{\text { opposite }} = \frac{3}{\sqrt{5}}\).
4. \(\cos U=\frac{3}{\sqrt{5}} \text { and } \csc U=\frac{2}{3}\). Incorrecto. Parece que cambiaste los valores de coseno y cosecante. Los nombres son muy similares, así que ten cuidado de usar la definición correcta. La respuesta correcta es C.

Relaciones entre las funciones trigonométricas

Las seis proporciones o funciones suelen considerarse como dos grupos de tres funciones. El primer grupo es:

\(\sin A=\dfrac{\text { opposite }}{\text { hypotenuse }}=\dfrac{o}{h}, \cos A=\dfrac{\text { adjacent }}{\text { hypotenuse }}=\dfrac{a}{h}, \tan A=\dfrac{\text { opposite }}{\text { adjacent }}=\dfrac{o}{a}\)

Una forma de recordar estas tres definiciones es con un dispositivo de memoria que utilice la primera letra de cada palabra. La definición de seno está representada por soh (seno equivale a opuesto sobre hipotenusa). Asimismo, la definición de coseno está representada por cah (coseno es igual a adyacente sobre hipotenusa), y la definición de tangente se representa por toa (tangente es igual a opuesta sobre adyacente). Armar estos te da sohcahtoa.

El segundo grupo es:

\(\csc A=\dfrac{\text { hypotenuse }}{\text { opposite }}=\dfrac{h}{o}, \sec A=\dfrac{\text { hypotenuse }}{\text { adjacent }}=\dfrac{h}{a}, \cot A=\dfrac{\text { adjacent }}{\text { opposite }}=\dfrac{a}{o}\)

Si comparas estas tres proporciones con las tres por encima de ellas, verás que estas tres fracciones son los recíprocos de las tres fracciones por encima de ellas. Es decir, cosecante es el recíproco de seno, secante es el recíproco del coseno, y cotangente es el recíproco de tangente. Escribir esto da tres identidades más:

\(\csc A=\frac{1}{\sin A}\)	\(\sec A=\frac{1}{\cos A}\)	\(\cot A=\frac{1}{\tan A}\)

Si recuerdas sohcahtoa más estas tres identidades, puedes encontrar los valores de cualquier función trigonométrica, como se ve en el siguiente ejemplo.

Ejemplo

Problema: Para ángulo agudo\(A\),\(\sin A = \frac{7}{25}\) y\(\cos A = \frac{24}{25}\). Encuentra los valores de las otras cuatro relaciones trigonométricas para el ángulo\(A\).

Contestar

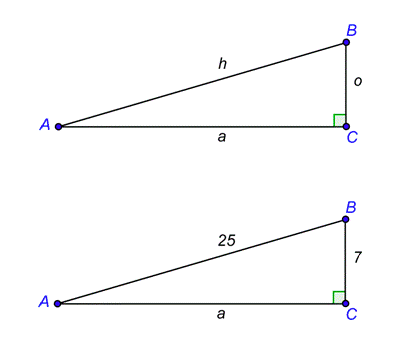
Eso te dice la definición de seno\(\sin A = \frac{o}{h} = \frac{7}{25}\). Un triángulo con o = 7 y h = 25 tendrá esta relación.

Eso también lo sabes\(\cos A = \frac{a}{h} = \frac{a}{25}\). Se te da\(\cos A = \frac{24}{25}\), entonces\(a = 24}\).

Ahora tienes los tres lados del triángulo y puedes usar la definición de tangente.

\(\tan A = \frac{o}{a} = \frac{7}{24}\)

A continuación, utilice las tres identidades recíprocas para obtener las otras tres proporciones.

\ (\ begin {array} {l}
\ csc A=\ frac {1} {\ sin A} =\ frac {1} {\ frac {7} {25}} =\ frac {25} {7}\
\ seg A=\ frac {1} {\ cos A} =\ frac {1} {24} =\ frac {25} {24}
\ cuna A=\ frac {1} {\ tan A} =\ frac {1} {\ frac {7} {24}} =\ frac {24} {7}
\ end {array}\)

\(\tan A=\frac{7}{24}, \csc A=\frac{25}{7}, \sec A=\frac{25}{24}, \cot A=\frac{24}{7}\)

El valor de cualquier función trigonométrica es una relación, o una fracción. Recuerda que las fracciones se pueden reducir.

Ejemplo

Problema: Para ángulo agudo\(A\),\(\cos A=\frac{3}{\sqrt{13}}\) y\(\tan A=\frac{4}{6}\). Encuentra los valores de\(\sin A\) y\(\csc A\).

Contestar

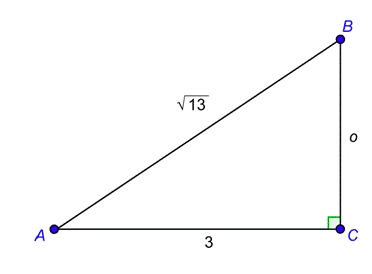
Quieres un triángulo rectángulo donde esté la relación del lado adyacente al ángulo\(A\) sobre la hipotenusa\(\frac{3}{\sqrt{13}}\). Un triángulo con lados\(a = 3\) y\(h = \sqrt{13}\) tendría esta relación.

Se puede utilizar la definición de tangente para encontrar el lado opuesto. Sustituya el valor que se le da por tangente y luego resuelva la ecuación.

\ (\ begin {array} {c}
\ tan A=\ frac {\ text {opuesto}} {\ texto {adyacente}} =\ frac {o} {3}\
\ frac {4} {6} =\ frac {o} {3}\
\ frac {12} {6} =o\\
2=o
\ end {array}\)

Ahora tienes los tres lados. Usa la definición de seno para encontrar su valor.

\(\sin A=\frac{o}{h}=\frac{2}{\sqrt{13}}\)

Ahora usando la identidad recíproca, la se\(\csc\) puede encontrar tomando el recíproco de la\(\sin\).

\(\sin A=\frac{2}{\sqrt{13}}, \csc A=\frac{\sqrt{13}}{2}\)

Recuerda que los lados de un triángulo rectángulo satisfacen el Teorema de Pitágoras. Entonces si\(a\) y\(b\) son las longitudes de las piernas, y\(c\) es la hipotenusa, debes tener\(a^2 + b^2 = c^2\). En el último ejemplo, las longitudes de las piernas eran 2 y 3, y la hipotenusa lo fue\(\sqrt{13}\), y es cierto que\(2^2 + 3^2 = \sqrt{13}^2\).

Ejercicio

¿Cuáles de las siguientes podrían ser los valores de las funciones trigonométricas del mismo ángulo?

1. \(\sin W=\frac{1}{\sqrt{5}}, \tan W=\frac{1}{2}, \csc W=\frac{\sqrt{5}}{2}\)
2. \(\sin X=\frac{4}{5}, \cos X=\frac{2}{5}, \sec X=\frac{5}{2}\)
3. \(\sin Y=\frac{12}{13}, \cos Y=\frac{5}{13}, \tan Y=\frac{5}{12}\)
4. \(\tan Z=1, \cos Z=\frac{1}{\sqrt{2}}, \cot Z=1\)

Contestar

1. \(\sin W=\frac{1}{\sqrt{5}}, \tan W=\frac{1}{2}, \csc W=\frac{\sqrt{5}}{2}\). Incorrecto. Se pueden tener estos valores de seno y tangente para el mismo ángulo. Sin embargo, los valores de seno y cosecante del mismo ángulo son recíprocos. Si\(\sin W = \frac{1}{\sqrt{5}}\), entonces\(\csc W = \frac{\sqrt{5}}{1}\), no\(\frac{\sqrt{5}}{2}\). La respuesta correcta es D.
2. \(\sin X=\frac{4}{5}, \cos X=\frac{2}{5}, \sec X=\frac{5}{2}\). Incorrecto. Los valores de coseno y secante son recíprocos, como deberían ser. Sin embargo, no se pueden tener los valores dados de seno y coseno para el mismo ángulo. Si\(\sin X = \frac{4}{5}\), puedes dibujar un triángulo rectángulo con el ángulo opuesto de la pierna\(X\) teniendo longitud 4 y teniendo la hipotenusa longitud 5. Si tiene\(\cos X = \frac{2}{5}\), entonces la longitud de la pierna adyacente es 2. Sin embargo, las longitudes 2, 4 y 5 no satisfacen el Teorema de Pitágoras. La respuesta correcta es D.
3. \(\sin Y=\frac{12}{13}, \cos Y=\frac{5}{13}, \tan Y=\frac{5}{12}\). Incorrecto. Se puede dibujar un triángulo rectángulo con el ángulo lateral opuesto\(Y\) teniendo longitud 12, el lado adyacente teniendo longitud 5, y teniendo la hipotenusa longitud 13. Esto te dará\(\sin Y=\frac{12}{13} \text { and } \cos Y=\frac{5}{13}\). Usando la definición de tangente\(\tan Y=\frac{\text { opposite }}{\text { adjacent }}\),, entonces tendrías\(\tan Y=\frac{12}{5}, \text { not } \frac{5}{12}\). La respuesta correcta es D.
4. \(\tan Z=1, \cos Z=\frac{1}{\sqrt{2}}, \cot Z=1\). Correcto. Si\(\tan Z = 1\), entonces\(\cot Z = 1\), porque son recíprocos. Se puede dibujar un triángulo rectángulo con ambas piernas teniendo longitud 1, y la hipotenusa tendrá longitud\(\sqrt{2}\) debido al Teorema de Pitágoras. Usando la definición de coseno\(\cos Z=\frac{\text { adjacent }}{\text { hypotenuse }}\),, entonces tendrás\(\cos Z=\frac{1}{\sqrt{2}}\).

Uso de una calculadora para encontrar los valores de las funciones trigonométricas

Sabes que si dibujas triángulos similares con medidas de ángulo\(35^{\circ}\),\(55^{\circ}\), y\(90^{\circ}\), la relación del lado opuesto\(35^{\circ}\) a la hipotenusa será la misma para todos esos triángulos. Esto es\(\sin 35^{\circ}\). La forma más fácil de encontrar lo que realmente equivale esta proporción es con una calculadora científica o gráfica.

Al mirar una calculadora, encontrarás una clave que dice SIN en ella. Puedes usar esto para encontrar el valor de\(\sin 35^{\circ}\). Ten esto en cuenta: necesitas saber que existen diferentes unidades para medir ángulos. Para nuestros propósitos, asegúrese de que su calculadora esté establecida en el “modo grado”. (Las siguientes instrucciones son generalizadas, pero es posible que deba consultar el manual de instrucciones de su calculadora para saber cómo realizar estos cálculos en su calculadora particular).

Si usa una calculadora científica, mire en la pantalla y vea si dice DEG en letras minúsculas por encima del 0 (a diferencia de RAD o GRAD). Si no lo hace, presione la tecla DRG hasta que la pantalla diga DEG. Ahora ingrese 35, y luego presione la tecla SIN. El resultado es\(\sin 35^{\circ}\):

\(\sin 35^{\circ}=0.573576436\)

Si tiene una calculadora gráfica, presione la tecla MODE. La tercera línea de la pantalla dirá RADIAN GRADO. Usa las flechas para seleccionar GRADO, luego presiona ENTER, 2ND, QUIT. Ahora la calculadora está en modo grados. En una calculadora gráfica, ingresas las cosas de la misma manera que las escribirías. Entonces presione las teclas para darle\(\sin (35)\) en la pantalla y luego presione ENTRAR. Ahora debería ver el valor en la siguiente línea de la pantalla.

Debido a que seno es una función, dada una medida de ángulo\(X\) (la entrada), su calculadora le dará el valor de\(\sin X\) (la salida). Todos los triángulos rectos con medida de ángulo agudo\(X\) serán similares, por lo que la relación del lado opuesto a la hipotenusa será la misma para todos esos triángulos. Por lo tanto, la relación depende únicamente del valor de\(X\); no depende del triángulo.

Asimismo, las otras cinco relaciones trigonométricas son funciones. Puedes usar tu calculadora para encontrar el valor de esas funciones. Notarás que junto a la clave SIN hay claves COS y TAN, las cuales pueden ser utilizadas para encontrar los valores de coseno y tangente.

Ejemplo

Problema: Usa tu calculadora para encontrar los valores de\(\cos 35^{\circ}\) y\(\tan 35^{\circ}\) a la milésima más cercana.

Contestar

En una calculadora científica, ingrese 35, luego presione COS. Haga esto en el orden inverso para una calculadora gráfica.

\(\cos 35^{\circ}=0.819152044\)

Recuerda mirar el lugar de las diez milésimas para ayudarte a redondear a la milésima más cercana.

\(\cos 35^{\circ} \approx 0.819\)

Utilice el mismo procedimiento para tangente.

\ (\ comenzar {alineado}
\ tan 35^ {\ circ} &=0.700207538\\
&\ aproximadamente 0.700
\ final {alineado}\)

\(\cos 35^{\circ} \approx 0.819 \text { and } \tan 35^{\circ} \approx 0.700\)

Es posible que hayas notado que tu calculadora no tiene claves para\(\csc\),\(\sec\), o\(\cot\). Aún puedes usarlo para encontrar los valores de estas funciones. Esto se puede hacer usando la calculadora en combinación con las identidades recíprocas. Primero debes encontrar el valor de\(\sin\),, o\(\cos\)\(\tan\), y luego encontrar el recíproco, como muestra este siguiente ejemplo.

Ejemplo

Problema: Usa tu calculadora para encontrar los valores de\(\csc 50^{\circ}\),\(\sec 50^{\circ}\), y\(\cot 50^{\circ}\) a la milésima más cercana.

Contestar

Primero usa tu calculadora para encontrar el valor de\(\sin 50^{\circ}\). No redondee este valor hasta que esté escribiendo la respuesta final.

\(\sin 50^{\circ}=0.766044443\)

Presiona la tecla que dice\(\frac{1}{x}\) o\(x^{-1}\). Esto te dará el valor de cosecante.

\(\csc 50^{\circ}=\frac{1}{\sin 50^{\circ}}=1.305407289\)

Ahora redondee su respuesta final a la milésima más cercana.

\(\csc 50^{\circ} \approx 1.305\)

Encuentra el valor de\(\cos 50^{\circ}\). Entonces encuentra el recíproco y redondear.

\ (\ begin {array} {c}
\ cos 50^ {\ circ} =0.64278761\\
\ sec 50^ {\ circ} =\ frac {1} {\ cos 50^ {\ circ}}\\
=1.555723827\
\ aproximadamente 1.556
\ final {array}\)

Encuentra el valor de\(\tan 50^{\circ}\). Entonces encuentra el recíproco y redondear.

\ (\ begin {array} {c}
\ tan 50^ {\ circ} =1.191753593\\
\ cot 50^ {\ circ} =\ frac {1} {\ tan 50^ {\ circ}}\\
=0.839099631\
\ aprox 0.839
\ end {array}\)

\(\csc 50^{\circ} \approx 1.305, \sec 50^{\circ} \approx 1.556, \text { and } \cot 50^{\circ} \approx 0.839\)

Ejercicio

¿Cuál es el valor de\(\csc 17^{\circ}\) a la milésima más cercana?

1. 3.420
2. 1.046
3. 0.001
4. -1.040

Contestar

1. 3.420. Correcto. Primero usa la calculadora para encontrar\(\sin 17^{\circ}=0.292371705\). Encuentra el recíproco de esto:\(\csc 17^{\circ}=3.42030362 \approx 3.420\)
2. 1.046. Incorrecto. Encontraste el valor de\(\sec 17^{\circ}\). Recuerda que cosecante es el recíproco de seno (no coseno). La respuesta correcta es 3.420.
3. 0.001. Incorrecto. Encontraste el valor de\(\sin \left(\frac{1}{17^{\circ}}\right)\). Primero hay que encontrar\(\sin 17^{\circ}\), luego encontrar el recíproco. La respuesta correcta es 3.420.
4. -1.040. Incorrecto. Su calculadora no estaba establecida en grados. Antes de hacer cualquier cálculo, asegúrate de que primero lo tienes establecido en grados. La respuesta correcta es 3.420.

Uso de una calculadora para encontrar medidas de ángulo

Hasta el momento has aprendido las definiciones de las seis funciones trigonométricas. Recuerda que una función tiene una entrada y una salida. Para cada una de estas funciones, la entrada es la medida del ángulo y la salida equivale a una cierta proporción de lados. Su calculadora puede ser utilizada para encontrar los valores de estas funciones. Por ejemplo, si el ángulo mide\(60^{\circ}\), el coseno del ángulo es 0.5. Esto se puede representar como\(\cos 60^{\circ}=0.5\).

Ahora, ¿y si la situación se revivirtiera? ¿Y si supieras el valor de la relación y quisieras saber el ángulo que la produjo? Es decir, ¿y si conocieras la salida de una función trigonométrica, y quisieras conocer la entrada? Por ejemplo, podrías saber que el coseno de algún ángulo es de 0.5 y quieres averiguar cuál es el ángulo. También puedes usar tu calculadora para encontrar estos valores.

En general, cuando inviertes la entrada y la salida de una función, lo que obtienes se llama función inversa. Su calculadora puede encontrar los inversos de seno, coseno y tangente. En el ejemplo anterior, en una calculadora científica ingresarías 0.5, presionarías la tecla 2ND, luego presionarías COS. El display mostraría 60. (¡Asegúrate de que tu calculadora esté establecida en grados!) Esto te dice que el ángulo es\(60^{\circ}\). En una calculadora gráfica, presionaría 2ND, luego COS, luego 0.5, y finalmente ENTRAR. (Tenga en cuenta que es posible que deba consultar el manual de instrucciones de su calculadora para saber cómo realizar estos cálculos en su calculadora particular).

Por encima de las claves SIN, COS, y TAN verás\(\sin ^{-1}, \cos ^{-1}\) y\(\tan ^{-1}\). Estas son las funciones trigonométricas inversas, y la manera de leerlas en voz alta es: arcoseno, arcoseno y arcoseno. El resultado mencionado anteriormente puede escribirse como\(\cos ^{-1} 0.5=60^{\circ}\) o\(\arccos 0.5=60^{\circ}\).

Si se le diera el valor de la función seno (o tangente) y quisiera saber qué ángulo la produjo, seguiría un procedimiento similar al descrito anteriormente. Entonces en una calculadora científica, ingresarías el valor, presionarías la tecla 2ND, luego presionarías SIN (o TAN).

Ejemplo

Problema: Usa tu calculadora para encontrar el ángulo, al grado más cercano, cuyo valor tangente es 0.75.

Contestar

En una calculadora científica, ingrese 0.75, luego presione la tecla 2ND y TAN. Haga esto en el orden inverso para una calculadora gráfica.

\(\tan ^{-1} 0.75=36.86989765^{\circ}\)

Mira el décimo lugar para ayudarte a redondear al grado más cercano.

\(36.86989765^{\circ} \approx 37^{\circ}\)

\(\tan ^{-1} 0.75 \approx 37^{\circ}\)

Si se le da la expresión\(\cos ^{-1} 0.24\), por ejemplo, puede interpretar esto como diciendo: “Encuentra el ángulo cuyo coseno es igual a 0.24”.

Ejemplo

Problema: Determinar\(\cos ^{-1} 0.24\) al décimo de grado más cercano.

Contestar

En una calculadora científica, ingrese 0.24, luego presione la tecla 2ND y COS. Haga esto en el orden inverso para una calculadora gráfica.

\(\cos ^{-1} 0.24=76.11345964^{\circ}\)

Mira el lugar de las centésimas para ayudarte a redondear a la décima más cercana.

\(76.11345964^{\circ} \approx 76.1^{\circ}\)

Recuerda que esto significa\(\cos 76.1^{\circ} \approx 0.24\).

\(\cos ^{-1} 0.24 \approx 76.1^{\circ}\)

Aquí hay un ejemplo del mundo real usando una función inversa.

Ejemplo

Problema: Una rampa para monopatín mide 7 pies de largo con un extremo en el suelo y el otro a 2 pies sobre el suelo. ¿Cuál es el ángulo de elevación al décimo de grado más cercano?

Contestar

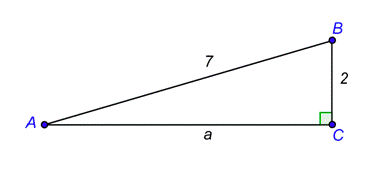
El ángulo de elevación es ángulo\(A\). Porque conoces el lado opuesto y la hipotenusa, puedes usar la función sinusoidal.

Usa la definición de seno. Lo desconocido es la entrada.

\(\sin A=\frac{2}{7}\)

Puedes reescribir esta ecuación usando arcsine. Es necesario invertir la entrada y la salida.

\(A=\sin ^{-1}\left(\frac{2}{7}\right)\)

En una calculadora científica, divida 2 por 7, luego presione la tecla 2ND y SIN. Haga esto en el orden inverso para una calculadora gráfica.

\ (\ begin {alineado}
A=&\ sin ^ {-1} 0.285714286\\
=& 16.6015496^ {\ circ}\\
&\ aproximadamente 16.6^ {\ circ}
\ end {alineado}\)

\(16.6^{\circ}\)

Recuerde que la función seno o coseno no puede tener una salida mayor a 1. Con arcsine y arccosine, está invirtiendo entradas y salidas. En consecuencia, la entrada de estas funciones no puede ser un número mayor que 1. Si intentas calcular\(\sin ^{-1} 2\) con tu calculadora, por ejemplo, recibirás un mensaje de error.

Ejercicio

Si\(\sin x = \frac{1}{3}\), ¿qué es\(x\) a la centésima de grado más cercana?

1. \(0.01^{\circ}\)
2. \(0.34^{\circ}\)
3. \(19.47^{\circ}\)
4. \(70.53^{\circ}\)

Contestar

1. \(0.01^{\circ}\). Incorrecto. En lugar de encontrar\(\sin ^{-1}\left(\frac{1}{3}\right)\), encontraste\(\sin \left(\frac{1}{3}\right)\). La respuesta correcta es\(19.47^{\circ}\).
2. \(0.34^{\circ}\). Incorrecto. No tenía su calculadora establecida en grados. Antes de hacer cualquier cálculo, asegúrate de que primero lo tienes establecido en grados. La respuesta correcta es\(19.47^{\circ}\).
3. \(19.47^{\circ}\). Correcto. La solución a la ecuación viene dada por la computación\(\sin ^{-1}\left(\frac{1}{3}\right)\).
4. \(70.53^{\circ}\). Incorrecto. En lugar de encontrar\(\sin ^{-1}\left(\frac{1}{3}\right)\), encontraste\(\cos ^{-1}\left(\frac{1}{3}\right)\). La respuesta correcta es\(19.47^{\circ}\).

Resumen

Las seis funciones trigonométricas se definen como relaciones de lados en un triángulo rectángulo. Sus valores dependen únicamente del ángulo y no de ningún triángulo rectángulo en particular. Una buena manera de recordar las definiciones de seno, coseno y tangente es con el dispositivo de memoria sohcahtoa. Las otras tres funciones, cosecante, secante y cotangente, son recíprocas de las tres primeras.

Puedes usar una calculadora para encontrar los valores de estas funciones o ratios. También puede utilizar una calculadora para encontrar los valores de las funciones trigonométricas inversas. Es decir, dada la relación, se puede encontrar el ángulo que la produjo.