19.1.2: Trigonometría de Triángulo Recto

Objetivos de aprendizaje

• Usa el Teorema de Pitágoras para encontrar las longitudes que faltan de los lados de un triángulo rectángulo.
• Encuentra las longitudes y ángulos faltantes de un triángulo rectángulo.
• Encuentre los valores exactos de la función trigonométrica para los ángulos que miden\(30^{\circ}\),\(45^{\circ}\), y\(60^{\circ}\).
• Resolver problemas aplicados mediante trigonometría de triángulo rectángulo.

Introducción

Supongamos que tienes que construir una rampa y no sabes cuánto tiempo tiene que ser. Conoces ciertas medidas de ángulo y longitudes laterales, pero necesitas encontrar las piezas de información que faltan.

Hay seis funciones trigonométricas, o ratios, que puedes usar para calcular lo que no sabes. Ahora aprenderá a usar estas seis funciones para resolver problemas de aplicaciones de triángulo rectángulo.

Uso del Teorema de Pitágoras en Problemas de Trigonometría

Hay varias formas de determinar la información faltante en un triángulo rectángulo. Una de estas formas es el Teorema de Pitágoras, que afirma que\(a^2 + b^2 = c^2\).

Supongamos que tiene un triángulo rectángulo en el que a y b son los largos de las piernas, y c es la longitud de la hipotenusa, como se muestra a continuación.

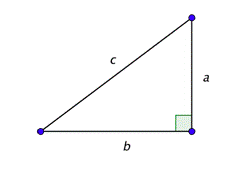
Si conoces la longitud de cualquiera de los dos lados, entonces puedes usar el Teorema de Pitágoras (\(a^2 + b^2 = c^2\)) para encontrar la longitud del tercer lado. Una vez que conoces todas las longitudes laterales, puedes calcular todas las funciones trigonométricas.

Ejemplo

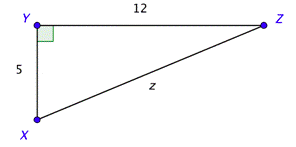
Problema: Encontrar los valores de\(tan X\) y\(\sec X\).

Responder

De inmediato se puede encontrar la tangente a partir de la definición y la información en el diagrama.

\(\tan X=\frac{\text { opposite }}{\text { adjacent }}=\frac{12}{5}\)

Para encontrar el valor de la secante, necesitarás la longitud de la hipotenusa. Usa el Teorema de Pitágoras para encontrar la longitud de la hipotenusa.

\ (\ begin {array} {c}
5^ {2} +12^ {2} =z^ {2}\\
25+144=z^ {2}\\
169=z^ {2}\\
13=z
\ end {array}\)

Ahora calcula\(\sec X\) usando la definición de secante.

\(\sec X=\frac{\text { hypotenuse }}{\text { adjacent }}=\frac{z}{5}=\frac{13}{5}\)

\(\tan X=\frac{12}{5}, \sec X=\frac{13}{5}\)

Ejercicio

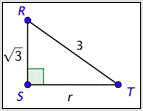
¿Cuál es el valor de\(\csc R\)?

1. \(\frac{\sqrt{3}}{3}\)
2. \(\frac{3}{\sqrt{3}}\)
3. \(\frac{3}{\sqrt{6}}\)
4. \(\frac{3}{\sqrt{12}}\)

Responder

1. \(\frac{\sqrt{3}}{3}\). Incorrecto. Encontraste\(\cos R\) en vez de\(\csc R\). Usa el Teorema de Pitágoras para encontrar la longitud del lado opuesto. Luego divide la hipotenusa por la longitud opuesta. La respuesta correcta es\(\frac{3}{\sqrt{6}}\).
2. \(\frac{3}{\sqrt{3}}\). Incorrecto. Parece que usaste el ángulo equivocado y lo encontraste\(\csc T\). Recuerda que los dos ángulos agudos te darán diferentes valores de función trigonométrica. Usa el Teorema de Pitágoras para encontrar la longitud del lado opuesto. Divida la hipotenusa por la longitud opuesta. La respuesta correcta es\(\frac{3}{\sqrt{6}}\).
3. \(\frac{3}{\sqrt{6}}\). Correcto. Necesitas conocer la longitud del lado opuesto, así que usa el Teorema de Pitágoras:\((\sqrt{3})^{2}+r^{2}=3^{2}\). Esto simplifica a\(3 + r^2 = 9\). Resolver esta ecuación te da\(r = \sqrt{6}\). Utilizando la definición de cosecante,\(\csc R=\frac{\text { hypotenuse }}{\text { opposite }}=\frac{3}{r}=\frac{3}{\sqrt{6}}\).
4. \(\frac{3}{\sqrt{12}}\). Incorrecto. Probablemente usó la definición correcta,\(\csc R=\frac{\text { hypotenuse }}{\text { opposite }}\), y usó el Teorema de Pitágoras para encontrar la longitud del lado opuesto,\(r\), pero configuró la ecuación incorrectamente. Debería serlo\((\sqrt{3})^{2}+r^{2}=3^{2}\). La respuesta correcta es\(\frac{3}{\sqrt{6}}\).

Algunos problemas pueden proporcionarle los valores de dos relaciones trigonométricas para un ángulo y pedirle que encuentre el valor de otras relaciones. Sin embargo, realmente solo necesitas conocer el valor de una relación trigonométrica para encontrar el valor de cualquier otra relación trigonométrica para el mismo ángulo.

Ejemplo

Problema: Para ángulo agudo\(A\),\(\tan A = \frac{2}{5}\). Encuentra los valores de\(\cos A\) y\(\sec A\).

Responder

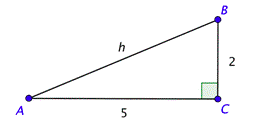
Primero necesitas dibujar un triángulo rectángulo en el que\(\tan A = \frac{2}{5}\).

La tangente es la relación del lado opuesto al lado adyacente. Se muestra el triángulo más simple que puedes usar que tenga esa proporción. Tiene un lado opuesto de longitud 2 y un lado adyacente de longitud 5. Podrías haber usado un triángulo que tiene un lado opuesto de longitud 4 y un lado adyacente de longitud 10. (Solo necesitas la relación para reducir a\(\frac{2}{5}\)).

Puedes usar el Teorema de Pitágoras para encontrar la hipotenusa.

\ (\ begin {array} {c}
5^ {2} +2^ {2} =h^ {2}\\
25+4 = h^ {2}\\
29=h^ {2}\
\ sqrt {29} =h
\ end {array}\)

Entonces usa la definición de coseno para encontrar\(\cos A\).

\(\cos A=\frac{\text { adjacent }}{\text { hypotenuse }}=\frac{5}{\sqrt{29}}\)

Ahora usa el hecho de que\(\sec A=\frac{1}{\cos A}\) para encontrar\(\sec A\).

\(\sec A=\frac{1}{\cos A}=\frac{1}{\frac{5}{\sqrt{29}}}=\frac{\sqrt{29}}{5}\)

\(\cos A=\frac{5}{\sqrt{29}}, \sec A=\frac{\sqrt{29}}{5}\)

Ejemplo

Problema: Si el ángulo\(X\) es un ángulo agudo con\(\sin X = \frac{3}{4}\), ¿cuál es el valor de\(\cot X\)?

Responder

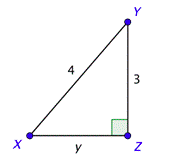
En este triángulo rectángulo, porque\(\sin X = \frac{3}{4}\), la relación del lado opuesto a la hipotenusa es\(\frac{3}{4}\). El triángulo más simple que podemos usar que tenga esa relación sería el triángulo que tiene un lado opuesto de longitud 3 y una hipotenusa de longitud 4.

Podemos usar el Teorema de Pitágoras para encontrar la longitud desconocida de la pierna.

\ (\ begin {array} {c}
y^ {2} +3^ {2} =4^ {2}\
y^ {2} +9=16\\
y^ {2} =7\\
y=\ sqrt {7}
\ end {array}\)

Puedes encontrar la cotangente usando la definición.

\(\cot X=\frac{\text { adjacent }}{\text { opposite }}=\frac{y}{3}=\frac{\sqrt{7}}{3}\)

O puedes encontrar la cotangente encontrando primero la tangente y luego tomando la recíproca.

\ (\ begin {array} {l}
\ tan X=\ frac {\ text {opuesto}} {\ texto {adyacente}} =\ frac {3} {y} =\ frac {3} {\ sqrt {7}}\
\ cot X=\ frac {1} {\ tan X} =\ frac {1} {\ frac {3} {\ sqrt {7}}} =\ frac {\ sqrt {7}} {3}
\ end {array}\)

\(\cot X=\frac{\sqrt{7}}{3}\)

Solución de triángulos rectos

Determinar todas las longitudes laterales y las medidas de ángulo de un triángulo rectángulo se conoce como resolver un triángulo rectángulo. Veamos cómo hacer esto cuando te dan una longitud lateral y una medida de ángulo agudo. Una vez que aprendas a resolver un triángulo rectángulo, podrás resolver muchas aplicaciones del mundo real, como el problema de rampa al comienzo de esta lección, y las únicas herramientas que necesitarás son las definiciones de las funciones trigonométricas, el Teorema de Pitágoras y una calculadora.

Ejemplo

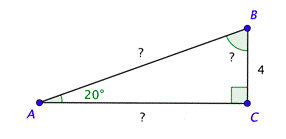
Problema: Es necesario construir una rampa con las siguientes dimensiones. Resuelve el triángulo rectángulo que se muestra a continuación. Usa las aproximaciones\(\csc 20^{\circ} \approx 2.92\) y\(\tan 20^{\circ} \approx 0.364\), y da las longitudes a la décima más cercana.

Responder

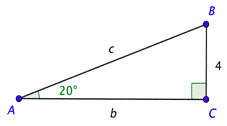
Recuerde que los ángulos agudos en un triángulo rectángulo son complementarios, lo que significa que su suma es\(90^{\circ}\). Ya que\(m \angle A=20^{\circ}\), se deduce que\(m \angle B=90^{\circ}-20^{\circ}=70^{\circ}\).

Puedes usar la definición de cosecante para encontrar\(c\). Sustituye la medida del ángulo en el lado izquierdo de la ecuación y usa el triángulo para establecer la relación a la derecha. Resolver la ecuación y redondear al décimo más cercano te da\(c \approx 11.7\).

\ (\ begin {array} {c}
\ csc 20^ {\ circ} =\ frac {\ text {hipotenusa}} {\ text {opuesto}}\\
2.92\ approx\ frac {c} {4}\\
4 (2.92)\ c aprox\\
11.68\ c aprox
\ end {array}\)

De manera similar, se puede utilizar la definición de tangente y la medida del ángulo para encontrar\(b\). Resolver la ecuación y redondear al décimo más cercano te da\(b \approx 11.0\).

\ (\ begin {array} {c}
\ tan 20^ {\ circ} =\ frac {\ text {opuesto}} {\ texto {adyacente}}\\
0.364\ approx\ frac {4} {b}\
0.364 b\ approx 4\\
b\ approx\ frac {4} {0.364}\ approx 10.989
\ end {array}\)

La rampa debe tener 11.7 pies de largo.

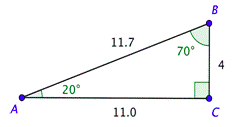
En el problema anterior, se le dieron los valores de las funciones trigonométricas. En el siguiente problema, necesitarás usar las teclas de función trigonométricas de tu calculadora para encontrar esos valores.

Ejemplo

Problema: Resuelve el triángulo rectángulo que se muestra a continuación. Dar las longitudes a la décima más cercana.

Responder

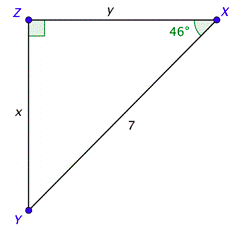
Los ángulos agudos son complementarios, lo que significa que su suma es\(90^{\circ}\). Ya que\(\text { Since } m \angle X=46^{\circ}\), se deduce que\(m \angle Y=90^{\circ}-46^{\circ}=44^{\circ}\).

Puedes usar la definición de seno para encontrar\(x\). Usa tu calculadora para encontrar el valor de\(\sin 46^{\circ}\) y el triángulo para configurar la relación a la derecha. Resolver la ecuación y redondear al décimo más cercano te da\(x \approx 5.0\).

\ (\ begin {array} {c}
\ sin 46^ {\ circ} =\ frac {\ texto {opuesto}} {\ texto {hipotenusa}}\\
0.72\ approx\ frac {x} {7}\\
7 (0.72)\ x aprox\\
5.04\ x aprox
\ end {array}\)

Para encontrar\(y\), puedes usar otra función trigonométrica (como el coseno) o bien puedes usar el Teorema de Pitágoras. Resolver la ecuación y redondear al décimo más cercano te da\(y \approx 4.9\).

\ (\ begin {array} {c}
5.0^ {2} +y^ {2}\ approx 7^ {2}\
25+y^ {2}\ approx 49\\
y^ {2}\ approx 24\\
y\ approx\ sqrt {24}\\
y\ approx 4.899
\ fin {array}\)

Ahora conocemos los tres lados y los tres ángulos. Sus valores se muestran en el dibujo.

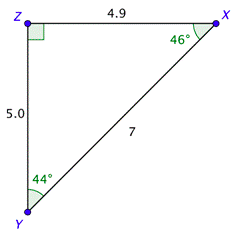
A veces se le puede dar suficiente información sobre un triángulo rectángulo para resolver el triángulo, pero esa información puede no incluir las medidas de los ángulos agudos. En esta situación, necesitarás usar las teclas de función trigonométricas inversas en tu calculadora para resolver el triángulo.

Ejemplo

Problema: Resuelve el triángulo rectángulo que se muestra a continuación, dado eso\(\cot N =\frac{4}{5}\). Encuentra las longitudes exactas de los lados y aproxima los ángulos al grado más cercano.

Responder

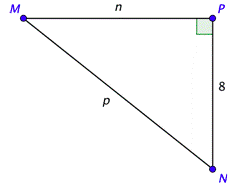
No se le da una medida de ángulo, pero puede usar la definición de cotangente para encontrar el valor de\(n\).

Usa la relación que te dan en el lado izquierdo y la información del triángulo en el lado derecho. Multiplicar y resolver para\(n\).

\ (\ comenzar {alineado}
\ cot N &=\ frac {\ texto {adyacente}} {\ texto {opuesto}}\\
\ frac {4} {5} &=\ frac {8} {n}\\
4 n &=40\\
n &=10
\ end {alineado}\)

Utilice el Teorema de Pitágoras para encontrar el valor de\(p\).

\ (\ begin {array} {c}
10^ {2} +8^ {2} =p^ {2}\\
100+64=p^ {2}\\
164=p^ {2}\
\ sqrt {164} =p
\ end {array}\)

Podemos usar el triángulo para encontrar un valor de la tangente y la clave de tangente inversa en su calculadora para encontrar el ángulo que produce ese valor. El redondeo al grado más cercano,\(\angle M\) es aproximadamente\(39^{\circ}\),\(M \approx 39^{\circ}\). Restar\(39^{\circ}\), de\(90^{\circ}\) a obtener\(N \approx 51^{\circ}\).

\ (\ begin {array} {c}
\ tan M=\ frac {8} {10} =0.8\\
M=\ tan ^ {-1} 0.8\\
M\ aproximadamente 38.7^ {\ circ}
\ end {array}\)

Ahora conocemos los tres lados y los tres ángulos. Sus valores se muestran en el dibujo.

Ejercicio

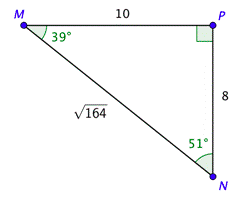
¿Cuál es el valor de\(x\) a la centésima más cercana?

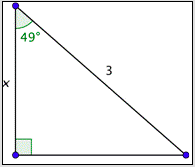
1. 4.57
2. 1.97
3. 0.90
4. 0.22

Responder

1. 4.57. Incorrecto. Probablemente configuraste la relación incorrectamente, igualando\(\cos 49^{\circ}\) y\(\frac{3}{x}\). Una forma correcta de configurar la ecuación es\(\cos 49^{\circ}=\frac{x}{3}\). La respuesta correcta es 1.97.
2. 1.97. Correcto. Una forma de establecer una ecuación correcta es usar la definición de coseno. Esto te dará\(\cos 49^{\circ}=\frac{x}{3}\). La solución a esta ecuación es:\(x=3 \cdot \cos 49^{\circ} \approx 3 \cdot(0.656)=1.968\). Esto ronda a 1.97.
3. 0.90. Incorrecto. Probablemente configuraste la ecuación correcta,\(\cos 49^{\circ}=\frac{x}{3}\), y la resolviste correctamente. Sin embargo, su calculadora no estaba establecida en grados. La respuesta correcta es 1.97.
4. 0.22. Incorrecto. Es posible que haya configurado correctamente su ecuación como\(\cos 49^{\circ}=\frac{x}{3}\), pero luego la resolvió incorrectamente como\(x=\frac{\cos 49^{\circ}}{3}\). La respuesta correcta es 1.97.

Ángulos Especiales

Como regla general, es necesario utilizar una calculadora para encontrar los valores de las funciones trigonométricas para cualquier medida de ángulo en particular. No obstante, los ángulos que miden\(30^{\circ}\)\(45^{\circ}\)\(60^{\circ}\), y, que verás en muchos problemas y aplicaciones, son especiales. Puedes encontrar los valores exactos de estas funciones sin una calculadora. Veamos cómo.

Supongamos que tenías un triángulo rectángulo con un ángulo agudo que medía\(45^{\circ}\). Dado que los ángulos agudos son complementarios, el otro también debe medir\(45^{\circ}\). Debido a que los dos ángulos agudos son iguales, las piernas deben tener la misma longitud, por ejemplo, 1 unidad.

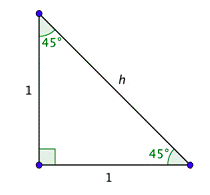
Se puede determinar la hipotenusa usando el Teorema de Pitágoras.

\ (\ begin {array} {c}
1^ {2} +1^ {2} =h^ {2}\\
1+1=h^ {2}\\
2=h^ {2}\
\ sqrt {2} =h
\ end {array}\)

Ahora tienes todos los lados y ángulos en este triángulo rectángulo.

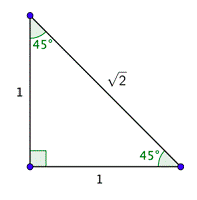
Puedes usar este triángulo (que a veces se llama\(90^{\circ}\) triángulo\(45^{\circ}\)\(45^{\circ}\) - -) para encontrar todas las funciones trigonométricas para\(45^{\circ}\). Una forma de recordar este triángulo es notar que la hipotenusa es\(\sqrt{2}\) multiplicada por la longitud de cualquiera de las piernas.

Ejemplo

Problema: Encontrar los valores de las seis funciones trigonométricas para denominadores\(45^{\circ}\) y racionalizar, si es necesario.

Responder

Usa las definiciones de seno, coseno y tangente. Observe que debido a que los lados opuestos y adyacentes son iguales, seno y coseno son iguales.

\ (\ begin {array} {c}
\ sin 45^ {\ circ} =\ frac {\ text {opuesto}} {\ texto {hipotenusa}} =\ frac {1} {\ sqrt {2}} =\ frac {1} {\ sqrt {2}}\ cdot\ frac {\ sqrt {2}} {\ sqrt {2}} =\ frac {\ sqrt {2}} {2}\
\ cos 45^ {\ circ} =\ frac {\ texto {adyacente}} {\ texto {hipotenusa}} =\ frac {1} {\ sqrt {2}} =\ frac {1} {\ sqrt {2}}\ cdot\ frac {\ sqrt {2}} {\ sqrt {2}} =\ frac {\ sqrt {2}} {2}\\
\ tan 45^ {\ circ} =\ frac {1} {1} =1
\ end {array}\)

Utilizar las identidades recíprocas. Observe que debido a que los lados opuestos y adyacentes son iguales, cosecante y secante son iguales.

\ (\ begin {array} {r}
\ csc 45^ {\ circ} =\ frac {1} {\ sin 45^ {\ circ}} =\ frac {1} {\ frac {1} {\ sqrt {2}}} =\ frac {\ sqrt {2}} {1} =\ sqrt {2}\
\ sec 45^ {\ circ} =\ frac {1} {\ cos 45^ {\ circ}} =\ frac {1} {\ frac {1} {\ sqrt {2}}} =\ frac {\ sqrt {2}} {1} =\ sqrt {2}\
\ cuna 45^ {\ circ} =\ frac {1} {tan\ 45^ {\ circ}} =\ frac {1} {1} =1
\ end {array}\)

\ (\ begin {array} {l}
\ sin 45^ {\ circ} =\ cos 45^ {\ circ} =\ frac {\ sqrt {2}} {2},\ tan 45^ {\ circ} =1\
\ csc 45^ {\ circ} =\ sec 45^ {\ circ} =\ sqrt {2},\ cot 45^ {\ circ} =1
\ end {array}\)

Puedes construir otro triángulo que puedas usar para encontrar todas las funciones trigonométricas para\(30^{\circ}\) y\(60^{\circ}\). Comienza con un triángulo equilátero con longitudes laterales iguales a 2 unidades. Si divide el triángulo equilátero por la mitad, produce dos triángulos con\(30^{\circ}\),\(60^{\circ}\) y\(90^{\circ}\) ángulos. Estos dos triángulos rectos son congruentes. Ambos tienen una hipotenusa de longitud 2 y una base de longitud 1.

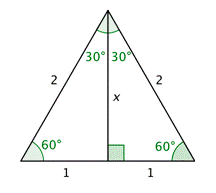
Se puede determinar la altura usando el Teorema de Pitágoras.

\ (\ begin {array} {c}
x^ {2} +1^ {2} =2^ {2}\
x^ {2} +1=4\
x^ {2} =3\\
x=\ sqrt {3}
\ end {array}\)

Aquí está la mitad izquierda del triángulo equilátero girada de costado.

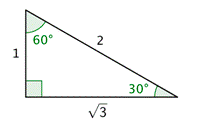
Puedes usar este triángulo (que a veces se llama\(90^{\circ}\) triángulo\(30^{\circ}\) -\(60^{\circ}\) -) para encontrar todas las funciones trigonométricas para\(30^{\circ}\) y\(60^{\circ}\). Tenga en cuenta que la hipotenusa es el doble de larga que la pierna más corta, que es opuesta al\(30^{\circ}\) ángulo, de manera que eso\(\sin 30^{\circ}=\frac{1}{2}\). La longitud de la pierna más larga, que es opuesta al\(60^{\circ}\) ángulo, es\(\sqrt{3}\) multiplicada por la longitud de la pierna más corta.

Ejemplo

Problema: Encontrar los valores de\(\cos 30^{\circ}\),\(\tan 60^{\circ}\),\(\sec 30^{\circ}\), y\(\cot 60^{\circ}\). Racionalizar los denominadores, si es necesario.

Responder

Usa las definiciones de seno, coseno y tangente. Para cada ángulo, asegúrese de usar las patas opuestas y adyacentes a ese ángulo. Por ejemplo,\(\sqrt{3}\) es opuesto a\(60^{\circ}\), pero adyacente a\(30^{\circ}\).

\ (\ begin {array} {r}
\ cos 30^ {\ circ} =\ frac {\ sqrt {3}} {2}\
\ tan 60^ {\ circ} =\ frac {\ sqrt {3}} {1} =\ sqrt {3}
\ end {array}\)

Recuerde que secante es el recíproco del coseno y que la cotangente es el recíproco de la tangente. Racionalizar los denominadores.

\ (\ begin {array} {r}
\ sec 30^ {\ circ} =\ frac {1} {\ frac {\ sqrt {3}} {2}} =\ frac {2} {\ sqrt {3}} =\ frac {2} {\ sqrt {3}}\ cdot\ frac {\ sqrt {3}} {\ sqrt {3} =\ frac {2\ sqrt {3}} {3}
\\ cuna 60^ {\ circ} =\ frac {1} {\ sqrt {3}} =\ frac {1} {\ sqrt {3}}\ cdot\ frac {\ sqrt {3}} {\ sqrt {3}} =\ frac {\ sqrt {3}}
\ end { matriz}\)

\ (\ begin {array} {l}
\ cos 30^ {\ circ} =\ frac {\ sqrt {3}} {2},\ seg 30^ {\ circ} =\ frac {2\ sqrt {3}} {3}\
\ tan 60^ {\ circ} =\ sqrt {3},\ cot 60^ {\ circ} =\ frac\ sqrt {3}} {3}
\ end {array}\)

Se puede utilizar la información de los\(90^{\circ}\) triángulos\(30^{\circ}\)\(60^{\circ}\) -\(45^{\circ}\) -\(90^{\circ}\) y\(45^{\circ}\) - - para resolver triángulos similares sin necesidad de utilizar una calculadora.

Ejemplo

Problema: ¿Cuál es el valor de\(x\) en el triángulo de abajo?

Responder

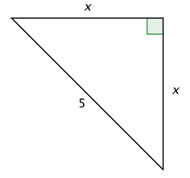
Dado que las dos patas tienen la misma longitud, los dos ángulos agudos deben ser iguales, por lo que son cada una\(45^{\circ}\).

En un\(45^{\circ}\)\(90^{\circ}\) triángulo, la longitud de la hipotenusa es multiplicada por la longitud de una pierna.\(45^{\circ}\) Puedes usar esta relación para encontrar\(x\). Recuerda racionalizar el denominador.

\ (\ comenzar {alineado}
\ sqrt {2}\ cdot x &=5\\
x &=\ frac {5} {\ sqrt {2}}\\
&=\ frac {5} {\ sqrt {2}}\ cdot\ frac {\ sqrt {2}} {\ sqrt {2}}\\
&=\ frac {5\ sqrt {2}} {2}
\ final {alineado}\)

Aquí hay otra forma de resolver este problema. Puedes usar la definición de seno para encontrar\(x\).

\ (\ begin {alineado}
\ sin 45^ {\ circ} &=\ frac {x} {5}\\
5\ cdot\ sin 45^ {\ circ} &=x\\
5\ cdot\ frac {1} {\ sqrt {2}} &=x\
\ frac {5} {\ sqrt {2}} &=x\\
x &= frac ac {5\ sqrt {2}} {2}
\ final {alineado}\)

\(x=\frac{5 \sqrt{2}}{2}\)

También podrías haber resuelto el último problema usando el Teorema de Pitágoras, que habría producido la ecuación\(x^2 + x^2 = 5^2\).

Ejemplo

Problema: Resuelve el triángulo rectángulo que se muestra a continuación.

Responder

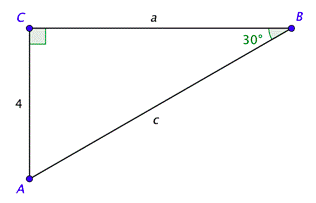
Los ángulos agudos son complementarios, entonces\(m \angle A=60^{\circ}\). Se trata\(30^{\circ}\) de\(60^{\circ}\) un\(90^{\circ}\) triángulo. Ahora podemos usar las funciones trigonométricas para encontrar las longitudes de los lados faltantes.

Como conocemos todas las medidas de los ángulos, ahora necesitamos encontrar las longitudes de los lados faltantes. Para encontrar\(c\) (la longitud de la hipotenusa), podemos usar la función sinusoidal porque sabemos eso\(\sin 30^{\circ}=\frac{1}{2}\) y conocemos la longitud del lado opuesto.

\ (\ begin {array} {c}
\ sin 30^ {\ circ} =\ frac {4} {c}\
\ frac {1} {2} =\ frac {4} {c}\
c=8
\ end {array}\)

Para encontrar\(a\) (la longitud del lado opuesto al ángulo\(A\)), podemos usar la función tangente porque sabemos eso\(\tan 60^{\circ}=\sqrt{3}\) y sabemos la longitud del lado adyacente.

\ (\ begin {array} {c}
\ tan 60^ {\ circ} =\ frac {a} {4}\
\ sqrt {3} =\ frac {a} {4}\\
4\ sqrt {3} =a
\ end {array}\)

Ahora conocemos los tres lados y los tres ángulos. Sus valores se muestran en el dibujo.

Ejercicio

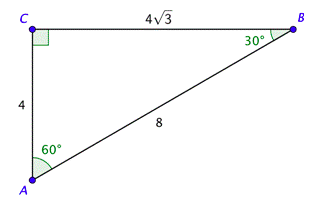
Si\(\cos x = \frac{1}{2}\), ¿cuál es el valor de\(\csc x\)?

1. 2
2. \(\frac{\sqrt{3}}{3}\)
3. \(\frac{\sqrt{6}}{3}\)
4. \(\frac{2 \sqrt{3}}{3}\)

Responder

1. 2. Incorrecto. Consulte el\(90^{\circ}\) triángulo\(30^{\circ}\)\(60^{\circ}\) - -. A partir de ahí se puede ver eso\(\cos 60^{\circ}=\frac{1}{2}\). De ello se deduce que\(x = 60^{\circ}\). Es posible que haya usado el ángulo incorrecto y encontrado\(\csc 30^{\circ}\) o usado el ángulo correcto pero encontrado\(\sec 60^{\circ}\). Necesitas encontrar\(\csc 60^{\circ}\). La respuesta correcta es\(\frac{2 \sqrt{3}}{3}\).
2. \(\frac{\Incorrect. Refer to the \(30^{\circ}\)-\(60^{\circ}\) -\(90^{\circ}\) triángulo. A partir de ahí se puede ver eso\(\cos 60^{\circ}=\frac{1}{2}\). De ello se deduce que\(x=60^{\circ}\). Es posible que hayas encontrado erróneamente\(\cot 60^{\circ}\). Necesitas encontrar\(\csc 60^{\circ}\). La respuesta correcta es\(\frac{2 \sqrt{3}}{3}\).
3. \(\frac{\sqrt{6}}{3}\). Incorrecto. Puede que hayas encontrado correctamente\(\csc 60^{\circ}\), pero cometiste un error al racionalizar el denominador. La respuesta correcta es\(\frac{2 \sqrt{3}}{3}\).
4. \(\frac{2 \sqrt{3}}{3}\). Correcto. Consulte el\(90^{\circ}\) triángulo\(30^{\circ}\)\(60^{\circ}\) - -. A partir de ahí se puede ver eso\(\cos 60^{\circ}=\frac{1}{2}\). De ello se deduce que\(x=60^{\circ}\). Entonces\(\csc x=\csc 60^{\circ}=\frac{2}{\sqrt{3}}=\frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{2 \sqrt{3}}{3}\).

Uso de la trigonometría en problemas del mundo real

Hay situaciones en el mundo real, como construir una rampa para un muelle de carga, en la que tienes un triángulo rectángulo con cierta información sobre los lados y ángulos, y deseas encontrar medidas desconocidas de lados o ángulos. Aquí es donde entender la trigonometría puede ayudarte.

Ejemplo

Problema: Ben y Emma están fuera volando una cometa. Emma puede ver que la cuerda de cometa que sostiene está haciendo un\(70^{\circ}\) ángulo con el suelo. La cometa está directamente encima de Ben, quien está parado a 50 pies de distancia. Al pie más cercano, ¿cuántos pies de cuerda ha soltado Emma?

Responder

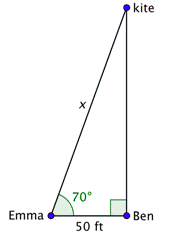
Queremos encontrar la longitud de la cuerda suelta. Es la hipotenusa del triángulo rectángulo que se muestra.

Dado que la distancia de 50 pies mide el lado adyacente al\(70^{\circ}\) ángulo, puede usar la función coseno para encontrar\(x\).

\(\cos 70^{\circ}=\frac{50}{x}\)

Resuelve la ecuación para\(x\). Usa una calculadora para encontrar un valor numérico. La respuesta ronda a 146.

\ (\ begin {array} {c}
x\ cdot\ cos 70^ {\ circ} =50\
x=\ frac {50} {\ cos 70^ {\ circ}}\\
x=\ frac {50} {0.342\ ldots}\\
x=146.19\ ldots
\ end {array}\)

Emma ha soltado aproximadamente 146 pies de cuerda.

En el ejemplo anterior, se le dio un lado y un ángulo agudo. En el siguiente, se le dan dos lados y se le pide que encuentre un ángulo. Encontrar un ángulo generalmente implica el uso de una función trigonométrica inversa. La letra griega theta,\(\theta\), se usa comúnmente para representar un ángulo desconocido. En este ejemplo,\(\theta\) representa el ángulo de elevación.

Ejemplo

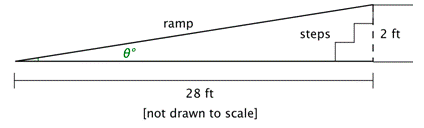
Problema: Se coloca una rampa para silla de ruedas sobre un conjunto de escaleras para que un extremo quede a 2 pies del suelo. El otro extremo está en un punto que está a una distancia horizontal de 28 pies de distancia, como se muestra en el diagrama. ¿Cuál es el ángulo de elevación al décimo de grado más cercano?

Responder

El ángulo de elevación está etiquetado\(\theta ^{\circ}\) en el diagrama. Las longitudes dadas son los lados opuestos y adyacentes a este ángulo, por lo que puede usar la función tangente para encontrar\(\theta\).

Quieres encontrar la medida de un ángulo que te dé un cierto valor tangente. Esto significa que necesitas encontrar la tangente inversa. Recuerda que tienes que usar las teclas 2ND y TAN en tu calculadora. Mira el lugar de las centésimas para redondear a la décima más cercana.

\ (\ begin {alineado}
\ tan\ theta^ {\ circ} &=\ frac {2} {28}\\\ tan\ theta^ {
\ circ} &=\ frac {1} {14}\\ theta^ {\ circ} &=\ tan ^ {-1}
\ izquierda (\ frac {1} {14}\ derecha)\\ theta^\ theta^ {\ theta^ {\ theta^ {\ theta^ {
\ theta^ {eta &=4.0856
\ ldots\ end {alineado}\)

El ángulo de elevación es aproximadamente\(4.1^{\circ}\).

Recuerde que los problemas que involucran triángulos con ciertos ángulos especiales se pueden resolver sin el uso de una calculadora.

Ejemplo

Problema: Se utiliza una barda para hacer un cerramiento triangular con el lado más largo igual a 30 pies, como se muestra a continuación. ¿Cuál es la longitud exacta del lado opuesto al\(60^{\circ}\) ángulo?

Responder

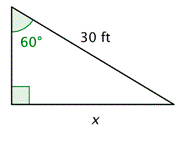
Llama a la longitud desconocida\(x\). Ya que conoces la longitud de la hipotenusa, puedes usar la función sinusoidal.

Se trata\(30^{\circ}\) de\(60^{\circ}\) un\(90^{\circ}\) triángulo. Por lo tanto, puede encontrar el valor exacto de la función trigonométrica sin usar una calculadora.

\ (\ begin {array} {l}
\ sin 60^ {\ circ} =\ frac {x} {30}\
\ frac {\ sqrt {3}} {2} =\ frac {x} {30}
\ end {array}\)

Resuelve la ecuación para\(x\).

\(x=\frac{30 \sqrt{3}}{2}=15 \sqrt{3}\)

La longitud exacta del lado opuesto al\(60^{\circ}\) ángulo es de 15\(\sqrt{3}\) pies.

A veces el triángulo rectángulo puede ser parte de un panorama más amplio.

Ejercicio

Un cable de sujeción está unido a un poste telefónico a 3 pies por debajo de la parte superior del poste, como se muestra a continuación. El cable tensor está anclado a 14 pies del poste telefónico y forma un\(64^{\circ}\) ángulo con el suelo. ¿Qué tan alto del poste está conectado el cable de sujeción? Redondea tu respuesta a la décima de pie más cercana.

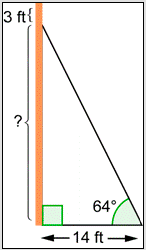
1. \(14 \cdot \sin 64^{\circ} \approx 12.6 \text { feet }\)
2. \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\)
3. \(14 \cdot \tan 64^{\circ}+3 \approx 31.7 \text { feet }\)
4. \(\frac{14}{\cos 64^{\circ}} \approx 31.9 \text { feet }\)

Responder

1. \(14 \cdot \sin 64^{\circ} \approx 12.6 \text { feet }\). Incorrecto. Es posible que te hayas confundido en cuanto a qué proporción corresponde a qué función trigonométrica. Es necesario resolver la ecuación\(\tan 64^{\circ}=\frac{x}{14}\), donde\(x\) representa la distancia vertical desde la base del poste telefónico hasta donde está unido el cable de tensado. La respuesta correcta es\(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
2. \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\). Correcto. Dejar\(x\) representar la distancia vertical desde la base del poste telefónico hasta donde está conectado el cable de sujeción. Entonces\(\tan 64^{\circ}=\frac{x}{14}\). Resolver esta ecuación para te\(x\) da\(x=14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
3. \(14 \cdot \tan 64^{\circ}+3 \approx 31.7 \text { feet }\). Incorrecto. Parece que configuraste y resolviste la ecuación correcta para encontrar la longitud desconocida. No obstante, malinterpretó el problema. Cuando agregaste el 3 encontraste la altura de todo el poste. La respuesta correcta es\(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
4. \(\frac{14}{\cos 64^{\circ}} \approx 31.9 \text { feet }\). Incorrecto. Parece que configuraste y resolviste una ecuación para encontrar la longitud del cable (la hipotenusa del triángulo). Es necesario resolver la ecuación\(\tan 64^{\circ}=\frac{x}{14}\), donde\(x\) representa la distancia vertical desde la base del poste telefónico hasta donde está unido el cable de tensado. La respuesta correcta es\(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).

Resumen

Hay muchas maneras de encontrar las longitudes laterales faltantes o las medidas de ángulo en un triángulo rectángulo. La resolución de un triángulo rectángulo se puede lograr utilizando las definiciones de las funciones trigonométricas y el Teorema de Pitágoras. Este proceso se llama resolver un triángulo rectángulo. Poder resolver un triángulo rectángulo es útil para resolver una variedad de problemas del mundo real, como la construcción de una rampa para sillas de ruedas.

Se pueden encontrar los valores exactos de las funciones trigonométricas para los ángulos que miden\(30^{\circ}\),\(45^{\circ}\), y\(60^{\circ}\). Puedes encontrar valores exactos para los lados en\(30^{\circ}\),\(45^{\circ}\), y\(60^{\circ}\) triángulos si recuerdas eso\(\sin 45^{\circ}=\frac{1}{\sqrt{2}}\) y\(\sin 30^{\circ}=\frac{1}{2}\). Para otras medidas de ángulo, es necesario utilizar una calculadora para encontrar valores aproximados de las funciones trigonométricas.