19.2.3: Amplitud y Periodo
- Page ID
- 111210
- Comprender la amplitud y el periodo.
- Grafica la función sinusoidal con cambios en amplitud y periodo.
- Grafica la función coseno con cambios en amplitud y periodo.
- Hacer coincidir una función sinusoidal o coseno con su gráfica y viceversa.
Introducción
Ya sabes graficar las funciones\(y = \sin x\) y\(y = \cos x\). Ahora aprenderás a graficar toda una “familia” de funciones sinusoidales y cosenales. Estas funciones tienen la forma\(y = a\sin bx\) o\(y = a\cos bx\), donde\(a\) y\(b\) son constantes.
Funciones Periódicas
Se utilizó la variable\(\theta\) anteriormente para mostrar un ángulo en posición estándar, y también nos referimos a las funciones seno y coseno como\(y = \sin \theta\) y\(y = \cos \theta\). A menudo las funciones seno y coseno se utilizan en aplicaciones que no tienen nada que ver con triángulos o ángulos, y la letra\(x\) se usa en lugar de\(\theta\) para la entrada (así como para etiquetar el eje horizontal). Entonces a partir de este punto en adelante, nos referiremos a estas mismas funciones como\(y = \sin x\) y\(y = \cos x\). Este cambio no afecta a las gráficas; siguen siendo las mismas.
Ya sabes que las gráficas de las funciones seno y coseno tienen un patrón de cerros y valles que se repiten. La longitud de este patrón repetitivo es\(2\pi\). Es decir, la gráfica de\(y = \sin x\) (o\(y = \cos x\)) en el intervalo [0,\(2\pi\)] se parece a la gráfica en el intervalo [\(2\pi, 4\pi\)] o [\(4\pi, 6\pi\)] o [\(-2\pi, 0\)]. Este patrón continúa en ambas direcciones para siempre.
La gráfica siguiente muestra cuatro repeticiones de un patrón de longitud\(2\pi\). Cada uno contiene exactamente una copia completa del patrón “cerro y valle”.
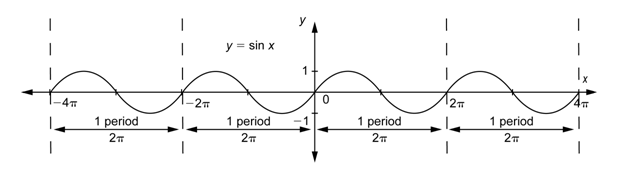
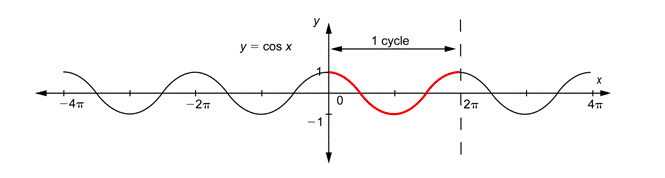
Si una función tiene un patrón repetitivo como seno o coseno, se llama función periódica. El periodo es la longitud del intervalo más pequeño que contiene exactamente una copia del patrón de repetición. Entonces el periodo de\(y = \sin x\) o\(y = \cos x\) es\(2\pi\). Cualquier parte de la gráfica que muestre este patrón a lo largo de un periodo se denomina ciclo. Por ejemplo, la gráfica de\(y = \cos x\) en el intervalo [0,\(2\pi\)] es un ciclo.
Sabes por graficar las funciones cuadráticas de la forma\(y = ax^2\) que a medida que cambiaste el valor de\(a\), cambiaste el “ancho” de la gráfica. Ahora veremos las funciones del formulario\(y = \sin bx\) y veremos cómo\(b\) afectarán los cambios a la gráfica. Por ejemplo, es\(y = \sin 2x\) periódico, y si es así, ¿cuál es el periodo? Aquí hay una tabla con algunas entradas y salidas para esta función.
para esta función.
| \(x\)(en radianes) | \(2x\)(en radianes) | \(\sin 2x\) |
| 0 | 0 | 0 |
| \(\frac{\pi}{6}\) | \(\frac{\pi}{3}\) | \(\frac{\sqrt{3}}{2}\) |
| \(\frac{\pi}{4}\) | \(\frac{\pi}{2}\) | 1 |
| \(\frac{\pi}{3}\) | \(\frac{2\pi}{3}\) | \(\frac{\sqrt{3}}{2}\) |
| \(\frac{\pi}{2}\) | \(\pi\) | 0 |
| \(\frac{2\pi}{3}\) | \(\frac{4\pi}{3}\) | \(-\frac{\sqrt{3}}{2}\) |
| \(\frac{3\pi}{4}\) | \(\frac{3\pi}{2}\) | -1 |
| \(\frac{5\pi}{6}\) | \(\frac{5\pi}{3}\) | \(-\frac{\sqrt{3}}{2}\) |
| \(\pi\) | \(2\pi\) | 0 |
Como los valores de\(x\) van de 0 a\(\pi\), los valores de\(2x\) van de 0 a\(2\pi\). Podemos ver en la gráfica que la función\(y = \sin 2x\) es una función periódica, y pasa por un ciclo completo en el intervalo [0,\(\pi\)], por lo que su periodo es\(\pi\). Si sustituyeras valores\(x\) de de\(\pi\) a\(2\pi\), los valores de\(2x\) pasarían de\(2\pi\) a\(4\pi\), y\(\sin 2x\) pasarían por otro ciclo completo de la función sinusoidal.
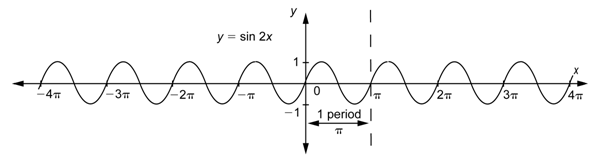
Observe que\(y = \sin 2x\) tiene dos ciclos en el intervalo [0,\(2\pi\)] que es el intervalo que\(y = \sin x\) necesita para completar un ciclo completo.
¿Cuál es el valor positivo más pequeño para\(x\) dónde\(y = \sin 2x\) está en su mínimo?
- \(-\frac{\pi}{4}\)
- \(\frac{\pi}{4}\)
- \(\frac{3\pi}{4}\)
- \(\frac{\pi}{2}\)
- Responder
-
- \(-\frac{\pi}{4}\). Incorrecto. La función sí alcanza su valor mínimo en este punto, pero no\(-\frac{\pi}{4}\) es un valor positivo. La respuesta correcta es\(\frac{3\pi}{4}\).
- \(\frac{\pi}{4}\). Incorrecto. Quizás confundiste mínimo y máximo. La respuesta correcta es\(\frac{3\pi}{4}\).
- \(\frac{3\pi}{4}\)Correcto. El valor mínimo para la función sinusoidal es -1. Mira la gráfica de\(y = \sin 2x\). Logra este mínimo en el fondo de cada valle. El fondo del primer valle donde\(x\) es positivo está en\(x = \frac{3\pi}{4}\).
- \(\frac{\pi}{2}\). Incorrecto. Puede que hayas pensado en 0 como el valor mínimo, pero la función sinusoidal toma valores negativos. La respuesta correcta es\(\frac{3\pi}{4}\).
¿Cuál es el periodo de la función\(y = \sin 3x\)? Aquí hay una tabla con algunas entradas y salidas para esta función.
| \(x\)(en radianes) | \(3x\)(en radianes) | \(\sin 3x\) |
| 0 | 0 | 0 |
| \(\frac{\pi}{9}\) | \(\frac{\pi}{3}\) | \(\frac{\sqrt{3}}{2}\) |
| \(\frac{\pi}{6}\) | \(\frac{\pi}{2}\) | 1 |
| \(\frac{2\pi}{9}\) | \(\frac{2\pi}{3}\) | \(\frac{\sqrt{3}}{2}\) |
| \(\frac{\pi}{3}\) | \(\pi\) | 0 |
| \(\frac{4\pi}{9}\) | \(\frac{4\pi}{3}\) | \(-\frac{\sqrt{3}}{2}\) |
| \(\frac{\pi}{2}\) | \(\frac{3\pi}{2}\) | -1 |
| \(\frac{5\pi}{9}\) | \(\frac{5\pi}{3}\) | \(-\frac{\sqrt{3}}{2}\) |
| \(\frac{2\pi}{3}\) | \(2\pi\) | 0 |
Como los valores de\(x\) van de 0 a\(\frac{2\pi}{3}\), los valores de\(3x\) van de 0 a\(2\pi\). Podemos ver a partir de la gráfica que\(y = \sin 3x\) pasa por un ciclo completo en el intervalo [0,\(\frac{2\pi}{3}\)], así es su periodo\(\frac{2\pi}{3}\).
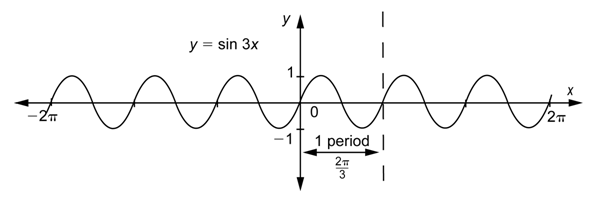
Observe que\(y = \sin 3x\) tiene tres ciclos en el intervalo [0,\(2\pi\)], que es el intervalo que\(y = \sin x\) necesita para completar un ciclo completo.
¿Cuál es el periodo de la función\(y=\sin \left(\frac{1}{2}\right) x\)? Aquí hay una tabla con algunas entradas y salidas para esta función.
| \(x\)(en radianes) | \(\frac{1}{2}x\)(en radianes) | \(\sin \left(\frac{1}{2}\right)\) |
| 0 | 0 | 0 |
| \(\frac{2\pi}{3}\) | \(\frac{\pi}{3}\) | \(\frac{\sqrt{3}}{2}\) |
| \(\pi\) | \(\frac{\pi}{2}\) | 1 |
| \(\frac{4\pi}{3}\) | \(\frac{2\pi}{3}\) | \(\frac{\sqrt{3}}{2}\) |
| \(2\pi\) | \(\pi\) | 0 |
| \(\frac{8\pi}{3}\) | \(\frac{4\pi}{3}\) | \(-\frac{\sqrt{3}}{2}\) |
| \(3\pi\) | \(\frac{3\pi}{2}\) | -1 |
| \(\frac{10\pi}{3}\) | \(\frac{5\pi}{3}\) | \(-\frac{\sqrt{3}}{2}\) |
| \(4\pi\) | \(2\pi\) | 0 |
Como los valores de\(x\) van de 0 a\(4\pi\), los valores de\(\frac{1}{2}x\) van de 0 a\(2\pi\).
Podemos ver a partir de la gráfica que\(y=\sin \left(\frac{1}{2} x\right)\) pasa por un ciclo completo en el intervalo\([0,4 \pi]\), así es su periodo\(4\pi\).
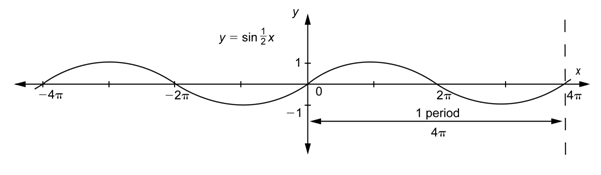
Observe que\(y=\sin \left(\frac{1}{2} x\right)\) tiene la mitad de un ciclo completo en el intervalo\(\left[0,2^{\pi}\right]\), que es el intervalo\(y=\sin x\)
Pongamos estos resultados en una tabla. Para las tres primeras funciones, hemos reescrito sus periodos con el numerador\(2\pi\) para que el patrón quede claro. ¿Se ve una relación entre la función y el denominador en los periodos? necesita completar un ciclo completo.
| Función | Periodo |
|---|---|
| \(y=\sin \left(\frac{1}{2} x\right)\) | \(4 \pi=\frac{2 \pi}{\frac{1}{2}}\) |
| \(y=\sin 1 x\) | \(2 \pi=\frac{2 \pi}{1}\) |
| \(y=\sin 2 x\) | \(\pi=\frac{2 \pi}{2}\) |
| \(y=\sin (3 x)\) | \(\frac{2 \pi}{3}=\frac{2 \pi}{3}\) |
En cada caso, el periodo se pudo encontrar dividiendo\(2\pi\) por el coeficiente de\(x\). En general, el periodo de\(y=\sin b x\) es\(\frac{2 \pi}{|b|}\), y el periodo de\(y=\cos b x\) es\(\frac{2 \pi}{|b|}\). Dado que el periodo es la longitud de un intervalo, siempre debe ser un número positivo. Ya que es posible\(b\) que sea un número negativo, debemos usar\(|b|\) en la fórmula para asegurarnos que el periodo,\(\frac{2 \pi}{|b|}\), sea siempre un número positivo.
El periodo de\(y=\sin b x\) o\(y=\cos b x\) es\(\frac{2 \pi}{|b|}\).
Se puede pensar en los diferentes valores de\(b\) como tener un efecto de “acordeón” (o un resorte) en las gráficas de seno y coseno. Un gran valor de los\(b\) aprieta y un pequeño valor de los\(b\) estira.
Hay otra manera de describir este efecto. En el intervalo [0,\(2\pi\)],\(y=\sin x\) pasa por un ciclo mientras que\(y=\sin 2 x\) pasa por dos ciclos. Si vuelves atrás y revisas todos los ejemplos anteriores, verás que\(y=\sin b x\) tiene\(|b|\) ciclos en el intervalo\([0,2 \pi]\). Asimismo,\(y=\cos b x\) tiene\(|b|\) ciclos en el intervalo [0,\(2\pi\)].
Problema: ¿Cuáles son los periodos de\(y=\sin 4 x\) y\(y=\cos \left(-\frac{1}{2} x\right)\)?
Responder
Para\(y=\sin 4 x\),\(b = 4\). Sustituya este valor en la fórmula.
\(\text { period }=\frac{2 \pi}{|b|}=\frac{2 \pi}{4}=\frac{\pi}{2}\)
Para\(y=\cos \left(-\frac{1}{2} x\right)\),\(b = -\frac{1}{2}\).
\ (\ begin {array} {c}
\ text {period} =\ frac {2\ pi} {|b|} =\ frac {2\ pi} {\ izquierda|-\ frac {1} {2}\ derecha|} =\ frac {2\ pi} {\ frac {1} {2}}\\
=\ frac {2\ pi} {1}\ cdot\ frac {2} {1} =4\ pi
\ end {array}\)
El periodo de\(y=\sin 4 x\) es\(\frac{\pi}{2}\), y el periodo de\(y=\cos \left(-\frac{1}{2} x\right)\) es\(4\pi\).
Amplitud
Como has visto, las gráficas de todas estas funciones seno y coseno alternan entre cerros y valles. La altura de un cerro (que equivale a la profundidad de un valle) se llama amplitud. Se puede ver que para todas las gráficas que hemos mirado hasta ahora, la amplitud es igual a 1.
La forma formal de decir esto para cualquier función periódica es:
\(\text { amplitude }=\frac{\operatorname{maximum}-\operatorname{minimum}}{2}\)
Se sabe que el valor máximo de\(y=\sin x\) o\(y=\cos x\) es 1 y el valor mínimo de cualquiera es -1. Entonces, si aplicas la definición anterior, obtendrías:
\(\text { amplitude }=\frac{1-(-1)}{2}=\frac{1+1}{2}=\frac{2}{2}=1\)
Este resultado concuerda con lo observado a partir de la gráfica.
Has visto que cambiando el valor de\(b\) en\(y=\sin b x\) o\(y=\cos b x\) bien estira o aprieta la gráfica como un acordeón o un resorte, pero no cambia los valores máximos o mínimos. Para todas estas funciones, el máximo es 1 y el mínimo es -1. Entonces, si aplicas la definición de amplitud, estarías haciendo exactamente el mismo cálculo que acabamos de hacer anteriormente. La amplitud de cualquiera de estas funciones es 1.
Veamos un tipo diferente de cambio a una función graficando la función\(y=2 \sin x\). Aquí hay una tabla con algunos valores de esta función.
| \(x\)(en radianes) | \(\sin x\) | \(2 \sin x\) |
| 0 | 0 | 0 |
| \(\frac{\pi}{6}\) | \(\frac{1}{2}\) | 1 |
| \(\frac{\pi}{4}\) | \(\frac{\sqrt{2}}{2}\) | \(\sqrt{2}\) |
| \(\frac{\pi}{3}\) | \(\frac{\sqrt{3}}{2}\) | \(\sqrt{3}\) |
| \(\frac{\pi}{2}\) | 1 | 2 |
| \(\frac{2\pi}{3}\) | \(\frac{\sqrt{3}}{2}\) | \(\sqrt{3}\) |
| \(\frac{3\pi}{4}\) | \(\frac{\sqrt{2}}{2}\) | \(\sqrt{2}\) |
| \(\frac{5\pi}{6}\) | \(\frac{1}{2}\) | 1 |
| \(\pi\) | 0 | 0 |
Tomaremos la primera y tercera columnas para formar parte de la gráfica y luego extender ese patrón hacia la izquierda y hacia la derecha.
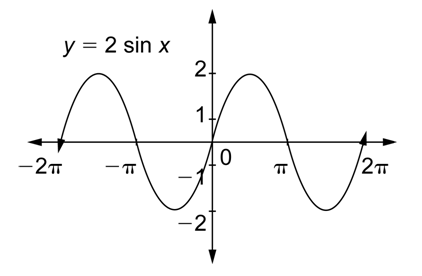
Ahora puedes usar esta gráfica en el siguiente ejemplo.
Problema: ¿Cuál es la amplitud de\(y = 2\sin x\)?
Responder
Puedes encontrar los valores máximo y mínimo de la función en la gráfica. Por ejemplo, en\(x = \frac{\pi}{2}\) el valor es 2, y en\(x = -\frac{\pi}{2}\) el valor es -2.
\ (\ begin {array} {c}
\ text {maximum} =2\\
\ text {mínimo} =-2
\ end {array}\)
Usa la definición de amplitud.
\(\text { amplitude }=\frac{2-(-2)}{2}=\frac{2+2}{2}=\frac{4}{2}=2\)
Observe que la altura de cada cerro es 2, y la profundidad de cada valle es 2. Esto es igual a la amplitud, como mencionamos al inicio.
Observe también que la amplitud es igual al coeficiente de la función:\(y = 2\sin x\)
Esto no es una coincidencia.
La amplitud es 2.
Comparemos la gráfica de esta función con la gráfica de la función sinusoidal.
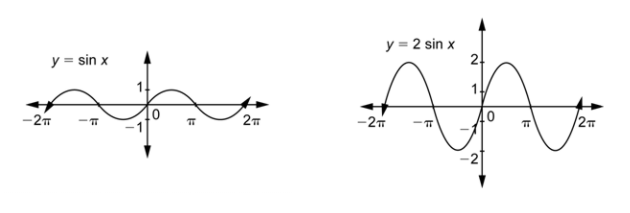
El efecto de multiplicar\(\sin x\) por 2 es estirar la gráfica verticalmente por un factor de 2. Debido a que se ha estirado verticalmente por este factor, la amplitud es el doble, o 2. Si hubiéramos mirado\(y = 3\sin x\), la gráfica se habría estirado verticalmente por un factor de 3, y la amplitud de esta función es 3. Nuevamente, esto es igual al coeficiente de la función. En general, tenemos la siguiente regla.
La amplitud de\(y = a\sin bx\) o\(y = a\cos bx\) es |\(a\) |.
Como el último ejemplo,\(y = 2\sin x\), muestra, multiplicar por una constante en el exterior afecta la amplitud. Si multiplicas por una constante en el exterior y en el interior, como en\(y = -3\sin 2x\), afectarás tanto a la amplitud como al periodo. Aquí está la gráfica de\(y = -3\sin 2x\):
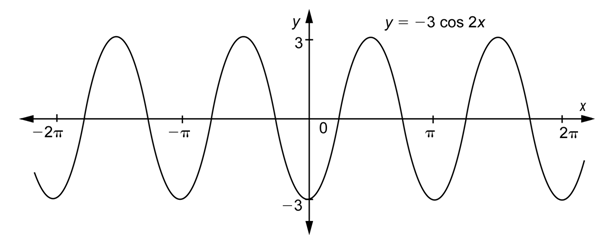
Problema: Determinar la amplitud y periodo de\(y = -3\cos 2x\).
Responder
Utilice la fórmula para la amplitud, con\(a = -3\).
\(\text { amplitude }=|a|=|-3|=3\)
Utilice la fórmula para periodo, con\(b = 2\).
\(\text { period }=\frac{2 \pi}{|b|}=\frac{2 \pi}{2}=\pi\)
La amplitud es 3 y el periodo es\(\pi\).
En este ejemplo, podrías haber encontrado el periodo mirando la gráfica anterior. Se muestra un ciclo completo, por ejemplo, en el intervalo [0,\(\pi\)], así es el periodo\(\pi\).
En las funciones\(y = a\sin bx\) y\(y = a\cos bx\), multiplicar por la constante\(a\) sólo afecta la amplitud, no el periodo. Como dijimos antes, cambiar el valor de\(b\) sólo afecta al periodo, no a la amplitud. El resultado general es el siguiente.
La amplitud de\(y = a\sin bx\) o\(y = a\cos bx\) es |\(a\) |.
El periodo de\(y = a\sin bx\) o\(y = a\cos bx\) es\(\frac{2 \pi}{|b|}\).
Actividad interactiva suplementaria
Para ayudarte a entender los cambios en la amplitud y el periodo tanto para la función sinusoidal como para la función coseno, prueba el siguiente ejercicio interactivo.
* Insertar Actividad Interactiva
¿Cuáles son la amplitud y el periodo de\(y = \frac{1}{2}\sin 4x\)?
- La amplitud es\(\frac{1}{2}\), y el periodo es\(\frac{\pi}{2}\).
- La amplitud es\(\frac{1}{2}\), y el periodo es\(8\pi\).
- La amplitud es 1, y el periodo es\(\frac{\pi}{2}\).
- La amplitud es 1, y el periodo es\(8\pi\).
- Responder
-
- Correcto. En esta función,\(a = \frac{1}{2}\), entonces esta es la amplitud. El periodo es igual\(\frac{2 \pi}{|b|}=\frac{2 \pi}{4}=\frac{\pi}{2}\).
- Incorrecto. La amplitud es correcta, pero el periodo no lo es. Probablemente multiplicaste\(2\pi\) por 4 en vez de dividirlo. La respuesta correcta es A.
- Incorrecto. El periodo es correcto, pero la amplitud no lo es. Puede que hayas pensado que la amplitud es la máxima menos la mínima, pero es la mitad de esto. La respuesta correcta es A.
- Incorrecto. Puede que hayas pensado que la amplitud es la máxima menos la mínima, pero es la mitad de esto. Probablemente multiplicaste\(2\pi\) por 4, en lugar de dividir, para encontrar el periodo. La respuesta correcta es A.
Gráficas de Funciones Senoidales
Sabes que la función\(y=a \sin b x\) tiene amplitud\(|a|\) y periodo\(\frac{2 \pi}{|b|}\). Puede utilizar estos hechos para dibujar la gráfica de cualquier función en el formulario\(y=a \sin b x\) iniciando con la gráfica de\(y = \sin x\) y modificándola.
Por ejemplo, supongamos que quería la gráfica de\(y=4 \sin x\). Ya que\(b = 1\), esta función tiene el mismo periodo que\(y = \sin x\). Ya que\(a = 4\), la amplitud es 4. Por lo tanto, tomarías la gráfica de\(y = \sin x\) y simplemente la estirarías verticalmente por un factor de 4. Aquí hay un ciclo para estas dos funciones.
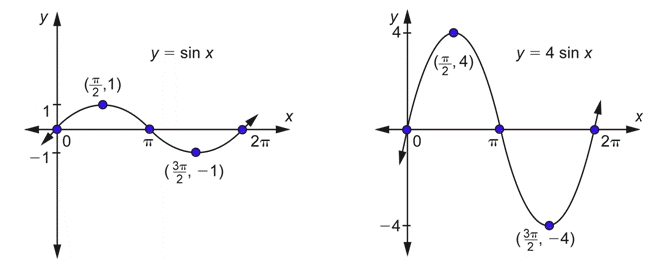
Tenga en cuenta que los puntos que estaban en el\(x\) eje -eje “permanecen” en el\(x\) eje. En estos puntos (donde\(x=0, \pi, 2 \pi\)), el valor de\(\sin x\) es 0. Si multiplicas 0 por 4 (o cualquier otra cosa), seguirás teniendo un valor de 0. Por lo que los puntos seguirán estando en el\(x\) eje -eje. Por otro lado, los puntos más altos y más bajos se han alejado del\(x\) eje -eje. Tenían\(y\) -valores de 1 y -1 para\(\sin x\), y tienen\(y\) -valores de 4 y -4 para\(4\sin x\).
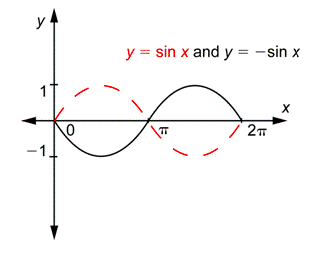
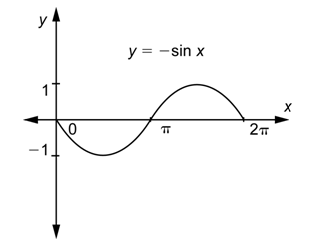
Problema: Gráfica\(y = -\sin x\) sobre el intervalo [0,\(2\pi\)].
Responder
El valor de\(b\) es 1, por lo que la gráfica tiene un periodo de\(2\pi\), al igual que lo hace\(y = \sin x\).
El valor de\(a\) es -1, por lo que la gráfica tiene una amplitud de 1, al igual que lo hace\(y = \sin x\).
Aunque la amplitud y el periodo son los mismos que la función\(y = \sin x\), la gráfica no es exactamente la misma. El efecto de multiplicar por -1 es reemplazar\(y\) -valores por sus opuestos. Entonces la gráfica de\(y = \sin x\) se refleja sobre el\(x\) eje -eje.
Si desea verificar estos gráficos con una calculadora gráfica, asegúrese de que la ventana gráfica tenga la configuración correcta. Para este último ejemplo, usarías\(0 \leq x \leq 2 \pi\) y\(-1 \leq y \leq 1\). En general, probablemente querrás ajustar los\(x\) valores -para mostrar un ciclo completo y los\(y\) valores -usando la amplitud.
Si los valores de\(a\) y\(b\) son ambos diferentes de 1, entonces necesitas combinar los efectos de los dos cambios.
Problema: Gráfica\(y=3 \sin \left(\frac{1}{2} x\right)\) sobre el intervalo [0,\(4\pi\)].
Responder
El valor de\(a\) es 3, por lo que la gráfica tiene una amplitud de 3. Esto tiene el efecto de tomar la gráfica de\(y = \sin x\) y estirarla verticalmente por un factor de 3.
El valor de\(b\) es\(\frac{1}{2}\), por lo que la gráfica tiene un periodo de\(\frac{2 \pi}{\frac{1}{2}}=\frac{2 \pi}{1} \cdot \frac{2}{1}=4 \pi\). Esto es el doble del periodo de\(y = \sin x\). Esto tiene el efecto de tomar la gráfica de\(y = \sin x\) y estirarla horizontalmente por un factor de 2. (La forma alternativa de decir esto es que\(y=3 \sin \left(\frac{1}{2} x\right)\) tiene\(\frac{1}{2}\) de un ciclo en el intervalo [0,\(2\pi\)].)
Para hacer la gráfica de\(y=3 \sin \left(\frac{1}{2} x\right)\), se deben combinar los dos efectos descritos anteriormente.
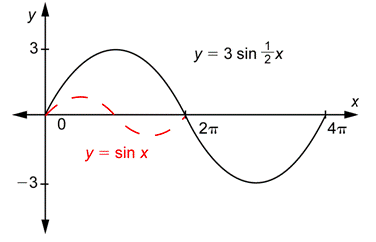
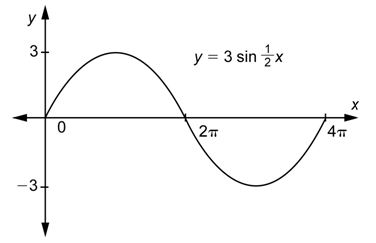
A veces necesitas estirar la gráfica de la función sinusoidal, y a veces necesitas encogerla.
Problema: Grafica dos ciclos de una función sinusoidal cuya amplitud es\(\frac{1}{2}\) y cuyo periodo es\(\frac{2 \pi}{3}\).
Responder
Existen diferentes funciones de la forma\(y=a \sin b x\) que se ajustan a esta descripción porque\(a\) y\(b\) podrían ser positivas o negativas. Dibujaremos la gráfica asumiendo que estos son positivos.
Debido a que la amplitud es\(\frac{1}{2}\), esto tiene el efecto de tomar la gráfica de\(y = \sin x\) y encogerla verticalmente en un factor de 2.
El periodo es\(\frac{2 \pi}{3}=\frac{1}{3} \cdot 2 \pi\), que es\(\frac{1}{3}\) el periodo de\(y = \sin x\). Esto tiene el efecto de tomar la gráfica de\(y = \sin x\) y encogerla horizontalmente por un factor de 3.
Para hacer la gráfica, se deben combinar los dos efectos descritos anteriormente.
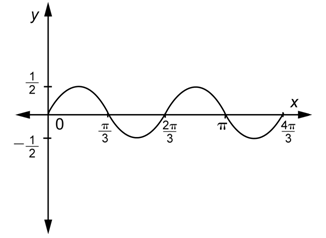
Incluso sin conocer el valor específico de una constante, a veces aún se pueden reducir las posibilidades de la forma de una gráfica.
La gráfica de una función\(y = a \sin x\), donde\(a\) es una constante, se dibuja en el intervalo\(0 \leq x \leq 2 \pi\). ¿Cuál de las siguientes opciones podría ser esta gráfica?
- Responder
-
- Incorrecto. Esto tiene la forma y el período correctos, pero está en la posición equivocada. Independientemente del valor de\(a\), la gráfica debe pasar por el\(x\) eje -en\(x=0, \pi, 2 \pi\), lo que no lo hace. La respuesta correcta es D.
- Incorrecto. Esta es la gráfica de una función coseno. Independientemente del valor de\(a\), la gráfica debe pasar por el\(x\) eje -en\(x=0, \pi, 2 \pi\). La respuesta correcta es D.
- Incorrecto. Debido a que el coeficiente de\(x\) es 1, la gráfica debe tener un periodo de\(2\pi\), pero esta gráfica tiene un periodo de\(\pi\). La respuesta correcta es D.
- Correcto. Debido a que el coeficiente de\(x\) es 1, la gráfica tiene un periodo de\(2\pi\), que tiene esta opción. El factor\(a\) podría estirar o encoger la gráfica, pero aún debe pasar por el\(x\) eje -en los puntos\(x=0, \pi, 2 \pi\), lo que hace.
Gráficas de Funciones de Coseno
Sabes que la función\(y=a \cos b x\) tiene amplitud\(|a|\) y periodo\(\frac{2 \pi}{|b|}\). Así como lo hiciste con las funciones sinusoidales, puedes usar estos hechos para dibujar la gráfica de cualquier función en el formulario\(y=a \cos b x\) comenzando con la gráfica de\(y = \cos x\) y modificándola.
Por ejemplo, supongamos que quería la gráfica de\(y=\cos \left(\frac{1}{2} x\right)\). Ya que\(a = 1\), tiene la misma amplitud que\(y = \cos x\). Y, porque\(b=\frac{1}{2}\), el periodo viene dado por:
\(\frac{2 \pi}{|b|}=\frac{2 \pi}{\frac{1}{2}}=\frac{2 \pi}{1} \cdot \frac{2}{1}=4 \pi\)
Dado que esto es el doble del periodo de\(y = \cos x\), tomarías la gráfica de\(y = \cos x\) y la estirarías horizontalmente por un factor de 2. Aquí hay una comparación lado a lado de estas dos gráficas.
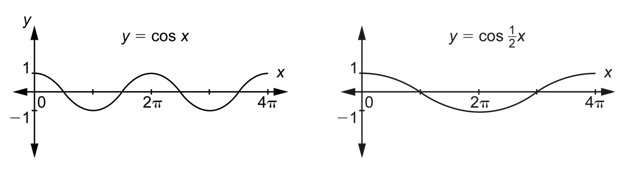
Tenga en cuenta que en el intervalo [0,\(2\pi\)], la gráfica de\(y = \cos x\) tiene un ciclo completo. Ya que\(b=\frac{1}{2}\), la gráfica de\(y=\cos \left(\frac{1}{2} x\right)\) has\(\frac{1}{2}\) de un ciclo en ese intervalo.
Si está utilizando una calculadora gráfica, debe ajustar la configuración de cada gráfica para obtener una ventana gráfica que muestre todas las características del gráfico. Para el último ejemplo, usarías\(0 \leq x \leq 4 \pi\) y\(-1 \leq y \leq 1\). En general, probablemente querrás ajustar los\(x\) valores -para mostrar un ciclo completo y los\(y\) -valores para mostrar los puntos más altos y más bajos. En el siguiente ejemplo, usarías\(-\pi \leq x \leq \pi\) y\(-2 \leq y \leq 2\) para la ventana gráfica porque se te pide específicamente que la grafiques sobre el dominio\([-\pi, \pi]\) y la gráfica tendrá una amplitud de 2, yendo tan baja como -2 y tan alta como +2.
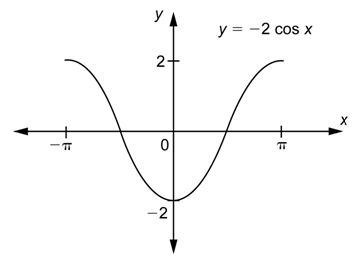
Problema: Gráfica\(y = -2 \cos x\) sobre el intervalo\([-\pi, \pi]\).
Responder
La amplitud es igual\(|a|=|-2|=2\). Esto tiene el efecto de tomar la gráfica de\(y = \cos x\) y estirarla verticalmente por un factor de 2. El signo negativo en el “exterior” tiene un efecto adicional: los\(y\) valores -son reemplazados por sus opuestos, por lo que la gráfica también se voltea sobre el\(x\) eje -eje.
El valor de\(b\) es 1, por lo que la gráfica tiene un periodo de\(2\pi\), al igual que lo hace\(y = \cos x\).
Cuando el único cambio es un estiramiento vertical, compresión o volteo, las\(x\) intercepciones siguen siendo las mismas. Entonces la gráfica pasará por el\(x\) eje -en\(-\frac{\pi}{2}\) y\(\frac{\pi}{2}\).
Nuevamente, si los valores de\(a\) y\(b\) son ambos diferentes de 1, es necesario combinar los efectos de los dos cambios. En el siguiente ejemplo, verás una variación que no has visto antes. Hasta este punto, todos los valores de\(b\) han sido números racionales, pero aquí estamos usando el número irracional\(\pi\). Esta situación no cambia realmente el procedimiento, pero verás que cambia la escala en el\(x\) eje -de una manera nueva.
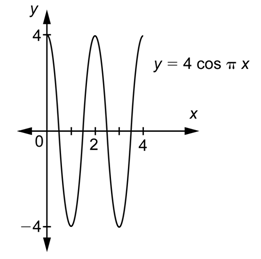
Problema: Gráfica\(y = 4 \cos \pi x\) sobre el intervalo [0, 4].
Responder
El valor de\(a\) es 4, por lo que la gráfica tiene una amplitud de 4. Esto tiene el efecto de tomar la gráfica de\(y = \cos x\) y estirarla verticalmente por un factor de 4.
El valor de\(b\) es\(\pi\), por lo que la gráfica tiene un periodo de\(\frac{2 \pi}{\pi}=2\). Esto tiene el efecto de reducir la gráfica de\(y = \cos x\) horizontalmente por un factor de\(\pi\), provocando que complete un ciclo completo en el intervalo [0, 2].
Observe el efecto sobre los\(x\) valores -de las intercepciones, los puntos altos y los puntos bajos. Debido a que el periodo es 2, el primer ciclo de la gráfica tendrá puntos altos en\(x = 0\) y 2. El punto bajo seguirá estando a medio camino entre estos, por lo que está en\(x = 1\). Los\(x\) -interceptos siguen a medio camino entre los puntos altos y bajos, por lo que estarán en\(x=\frac{1}{2}\) y\(\frac{3}{2}\). El segundo ciclo de la gráfica tiene todos estos puntos desplazados a la derecha 2 unidades.
Para hacer la gráfica de\(y = 4 \cos \pi x\), se deben combinar los efectos descritos anteriormente.
En dos ejemplos anteriores (\(y = -\sin x\)y\(y = -\cos x\)), viste que un signo negativo en el exterior (un valor negativo de\(a\)) tiene el efecto de voltear la gráfica alrededor del\(x\) eje -eje. En el siguiente ejemplo, verá el efecto de un signo negativo en el “interior” (un valor negativo de\(b\)).
Una última pista: además de intentar averiguar el efecto general del valor de\(a\) o\(b\) en la gráfica, es posible que desee verificar puntos específicos. Por ejemplo, simplemente sustituya\(x = 0\) en la función y vea dónde terminará ese punto.
¿Cuál de las siguientes opciones es\(y=\frac{3}{2} \cos (-x)\) la gráfica del intervalo\(-\pi \leq x \leq \pi\)?
- Responder
-
- Incorrecto. Esta es la gráfica de\(y=\frac{3}{2} \sin (-x)\). Recuerda revisar puntos específicos como\( = 0\). En ese punto,\(y=\frac{3}{2} \cos (0)=\frac{3}{2} \cdot 1=\frac{3}{2}\). Entonces el punto\(\left(0, \frac{3}{2}\right)\) debería estar en la gráfica. La respuesta correcta es C.
- Incorrecto. Confundiste los efectos de\(a\) y\(b\). Esta es la gráfica de\(y=-\cos \left(\frac{3}{2} x\right)\). La respuesta correcta es C.
- Correcto. El valor de\(a\) is\(\frac{3}{2}\), que estirará la gráfica verticalmente por un factor de\(\frac{3}{2}\). El periodo de la gráfica es\(\frac{2 \pi}{|-1|}=2 \pi\), al igual que el periodo de\(y = \cos x\). El efecto del signo negativo en el interior es reemplazar\(x\) -valores por sus opuestos. Esto volteará la gráfica alrededor del\(y\) eje. Sin embargo, debido a que la gráfica del coseno es simétrica alrededor del\(y\) eje -eje, esto no tiene ningún efecto en absoluto. Entonces el único cambio a la gráfica de\(y = \cos x\) es el estiramiento vertical.
- Incorrecto. Esta gráfica tiene el periodo y amplitud correctos. Sin embargo, has confundido el efecto de un signo menos en el interior con un signo menos en el exterior. La respuesta correcta es C.
Gráficas y funciones coincidentes
Dada cualquier función de la forma\(y=a \sin b x\) o\(y=a \cos b x\), ya sabes cómo encontrar la amplitud y el periodo y cómo usar esta información para graficar las funciones.
Dada una gráfica de una función sinusoidal o coseno, también se puede determinar la amplitud y el período de la función. A partir de esta información, puede encontrar valores de\(a\) y\(b\), y luego una función que coincida con la gráfica.
Recuerda que además de encontrar la amplitud y el periodo, es una buena idea mirar lo que está sucediendo\(x = 0\). Si\(a\) y\(b\) son constantes distintas de cero, las funciones\(y=a \sin b x\) y\(y=a \cos b x\) tendrán los siguientes valores en\(x = 0\):
\ (\ begin {array} {c}
y=a\ sin (b\ cdot 0) =a\ sin 0=a\ cdot 0=0\\
y=a\ cos (b\ cdot 0) =a\ cos 0=a\ cdot 1=a\ neq 0
\ end {array}\)
Esto te dice que la gráfica de\(y=a \sin b x\) pasa por (0, 0) independientemente de los valores de\(a\) y\(b\), y la gráfica de\(y=a \cos b x\) nunca pasa por (0, 0) independientemente de los valores de\(a\) y\(b\). Entonces, por ejemplo, si se le da una gráfica que pasa por el origen y se le pide que determine qué función representa, sabe de inmediato que no está en la forma\(y=a \cos b x\).
Hay que tener cuidado con el signo de\(a\). Podría determinar que una función tiene una amplitud de 4, por ejemplo. Aunque es posible eso\(a = 4\), también es posible eso\(a = -4\). Aquí un ejemplo de cada una de estas dos posibilidades.
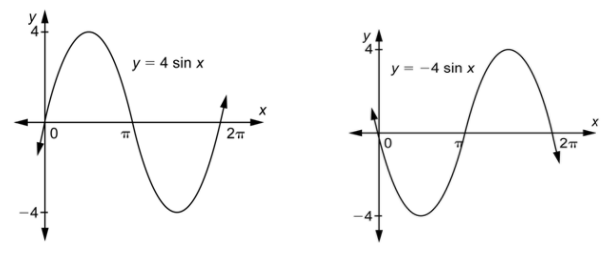
Necesitará comparar la gráfica con la de\(y = \sin x\) o\(y = \cos x\) para ver si, además de algún estiramiento o contracción, ha habido una reflexión sobre el\(x\) eje. La gráfica de arriba a la derecha se puede considerar como el resultado de estirar y reflejar la gráfica de\(y = \sin x\) a través del\(x\) eje. Si ha habido una reflexión, entonces el valor de\(a\) será negativo. Una vez que hayas determinado si\(a\) es positivo o negativo, siempre puedes elegir un valor positivo de\(b\).
Estos son algunos ejemplos de este proceso.
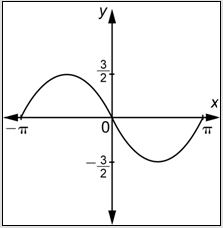
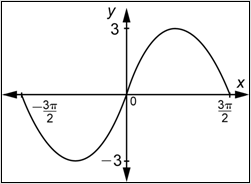
Problema: Determinar una función del formulario\(y=a \sin b x\) o\(y=a \cos b x\) cuya gráfica se muestra a continuación.
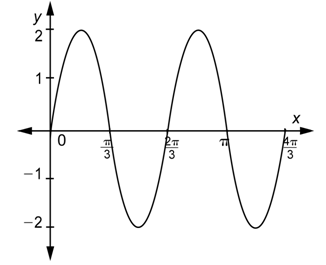
Responder
Primero, observa que la gráfica pasa por el origen, por lo que estás buscando una función de la forma\(y=a \sin b x\).
A continuación, observe que el valor máximo de la función es 2 y el mínimo es -2, por lo que la amplitud es 2. La gráfica tiene la misma “orientación” que\(y = \sin x\). (Comienza con un cerro a la derecha del\(y\) eje.) Esto implica que\(a\) es positivo, y en particular,\(a = 2\).
Finalmente, observe que la gráfica muestra dos ciclos y que un ciclo completo está contenido en el intervalo\(\left[0, \frac{2 \pi}{3}\right]\). Por lo tanto, el periodo es\(\frac{2 \pi}{3}\). Ya que\(\frac{2 \pi}{3}=\frac{2 \pi}{|b|}\),\(b=\pm 3\). De acuerdo con nuestro proceso, una vez que hayas determinado si\(a\) es positivo o negativo, siempre puedes elegir un valor positivo de\(b\). Entonces\(b = 3\).
Combina estas tres piezas de información.
\(y=2 \sin 3 x\)
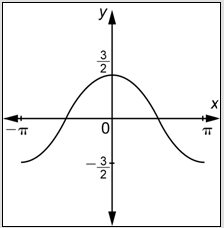
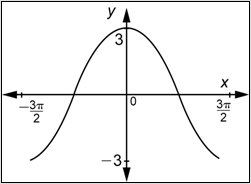
Problema: Determinar una función del formulario\(y=a \sin b x\) o\(y=a \cos b x\) cuya gráfica se muestra a continuación.
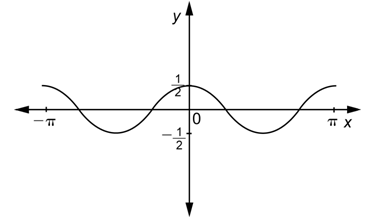
Responder
Primero, observa que la gráfica no pasa por el origen, sino crestas, alcanzando un máximo cuando\(x = 0\), por lo que estás buscando una función de la forma\(y=a \cos b x\).
A continuación, observar que el valor máximo de la función es\(\frac{1}{2}\) y el mínimo es\(-\frac{1}{2}\), por lo que la amplitud es\(\frac{1}{2}\). La gráfica tiene la misma “orientación” que\(y = \cos x\). (Tiene un cerro con el\(y\) eje -eje recorriendo el medio.) Esto implica que\(a\) es positivo, y en particular,\(a = \frac{1}{2}\).
Finalmente, observe que la gráfica muestra dos ciclos y que un ciclo completo está contenido en el intervalo [0,\(\pi\)]. Por lo tanto, el periodo es\(\pi\). Porque\(\pi=\frac{2 \pi}{|b|}\),\(b=\pm 2\). De acuerdo con nuestro proceso, una vez que hayas determinado si\(a\) es positivo o negativo, siempre puedes elegir un valor positivo de\(b\). Entonces\(b = 2\).
Combina estas tres piezas de información.
\(y=\frac{1}{2} \cos 2 x\)
Asegúrate de reconocer dónde comienza y termina un ciclo. El periodo es la duración del intervalo durante el cual transcurre un ciclo.
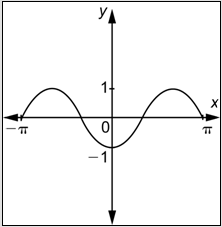
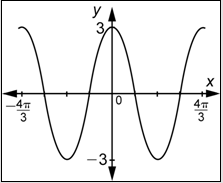
Problema: ¿Cuál de las siguientes funciones está representada por la siguiente gráfica?
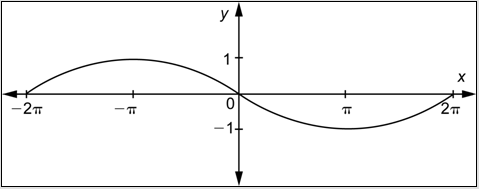
- \(y=-\sin x\)
- \(y=\sin \left(\frac{1}{2} x\right)\)
- \(y=-\sin 2 x\)
- \(y=-\sin \left(\frac{1}{2} x\right)\)
- Responder
-
- \(y=-\sin x\). Incorrecto. Reconoció correctamente la gráfica como una función sinusoidal reflejada, pero el periodo es incorrecto. Quizás viste el de\(2\pi\) la derecha y lo usaste como la duración de un ciclo. Sin embargo, toda la gráfica es de un ciclo, y el periodo es igual\(2 \pi-(-2 \pi)=4 \pi\). La respuesta correcta es D.
- \(y=\sin \left(\frac{1}{2} x\right)\). Incorrecto. Encontraste correctamente la amplitud y el periodo de esta función sinusoidal. Sin embargo, también es necesario verificar la orientación de la gráfica. Observe que a la derecha del\(y\) eje se tiene un valle en lugar de un cerro. La respuesta correcta es D.
- \(y=-\sin 2 x\). Incorrecto. Encontraste correctamente la amplitud y la orientación de esta función sinusoidal. No obstante, el periodo es incorrecto. Quizás reconoció que el periodo de la gráfica es el doble del periodo de\(y = \sin x\), y pensó que el valor de\(b\) sería 2. No obstante, para encontrar el valor de\(b\), se debe establecer el periodo igual a\(\frac{2 \pi}{|b|}\). La respuesta correcta es D.
- \(y=-\sin \left(\frac{1}{2} x\right)\). Correcto. La gráfica pasa por el origen, por lo que la función podría tener la forma\(y=a \sin b x\), pero no\(y=a \cos b x\). La amplitud es 1. La gráfica tiene un valle a la derecha, que podría ser el resultado de una reflexión\(y = \sin x\) sobre el\(x\) eje -eje. Por lo tanto,\(a = -1\). La gráfica muestra un ciclo, por lo que el periodo es\(4\pi\). Ya que\(4 \pi=\frac{2 \pi}{|b|}\), el valor de\(b\) podría ser\(\frac{1}{2}\). Entonces esta podría ser la gráfica de\(y=-\sin \left(\frac{1}{2} x\right)\).
Recuerda que al escribir una función puedes usar la notación\(f(x)\) en lugar de la variable\(y\).
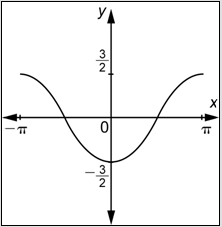
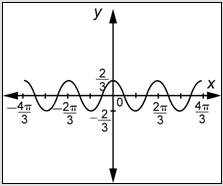
¿Cuál de las siguientes gráficas representa\(f(x)=3 \cos \left(\frac{2}{3} x\right)\)?
- Responder
-
- Incorrecto. Esta es la gráfica de una función de la forma\(f(x)=a \sin b x\). Recuerde verificar el valor de la función en\(x = 0\). Ya que\(f(0) = 3\), la función\(f(x)=3 \cos \left(\frac{2}{3} x\right)\) pasa a través de (0, 3), no el origen como se muestra en esta gráfica. La respuesta correcta es B.
- Correcto. En primer lugar, esta gráfica tiene la forma de una función coseno. Segundo, porque\(a = 3\) en la ecuación, la amplitud es 3. Por último, porque\(b=\frac{2}{3},\), el periodo de esta función es\(\frac{2 \pi}{\frac{2}{3}}=\frac{2 \pi}{1} \cdot \frac{3}{2}=3 \pi\). La gráfica en esta respuesta completa un ciclo completo entre\(x=-\frac{3}{2} \pi\) y\(x=\frac{3}{2} \pi\) así su periodo es\(\frac{3}{2} \pi-\left(-\frac{3}{2} \pi\right)=3 \pi\) según sea necesario.
- Incorrecto. Esta gráfica sí tiene la forma de una función coseno, y la amplitud es 3, lo cual es correcto. No obstante, el periodo es incorrecto. Probablemente multiplicaste\(2\pi\) por\(\frac{2}{3}\) en lugar de dividirte. La respuesta correcta es B.
- Incorrecto. Esta gráfica tiene la forma de una función coseno. Sin embargo, al determinar la gráfica, parece que cambiaste los valores de\(a\) y\(b\). La respuesta correcta es B.
Resumen
Las funciones\(y=a \sin b x\) y\(y=a \cos b x\) son funciones periódicas: sus gráficas tienen un patrón repetitivo de cerros y valles que continúa en ambas direcciones para siempre. La altura del cerro o la profundidad del valle se llama amplitud, y es igual a\(|a|\). Cualquier patrón completo en la gráfica se llama ciclo, y la longitud de un intervalo sobre el cual ocurre un ciclo se llama período. El periodo es igual al valor\(\frac{2 \pi}{|b|}\).
Puede usar esta información para graficar cualquiera de estas funciones comenzando con la gráfica básica de\(y = \sin x\) o\(y = \cos x\) y luego haciendo una combinación de estirar o encoger la gráfica verticalmente en función del valor de\(a\), estirando o encogiendo la gráfica horizontalmente en función del valor de \(b\), o reflejarlo en base a los signos de\(a\) y\(b\).
También puede comenzar con una gráfica, determinar los valores de\(a\) y\(b\), y luego determinar una función que representa.