19.2.2: Graficar las funciones de seno y coseno
- Page ID
- 111209
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Determinar las coordenadas de los puntos en el círculo unitario.
- Grafica la función sinusoidal.
- Grafica la función coseno.
- Compara las gráficas de las funciones seno y coseno.
Introducción
Ya sabes graficar muchos tipos de funciones. Los gráficos son útiles porque pueden tomar información complicada y mostrarla de una manera simple y fácil de leer. Ahora aprenderás a graficar las funciones seno y coseno, y verás que las gráficas de la función sinusoidal y la función coseno son muy similares.
Valores de las funciones de seno y coseno
Hemos visto un punto (\(x,y\)) en una gráfica de una función. La primera coordenada es la entrada o valor de la variable, y la segunda coordenada es la salida o valor de la función.
Cada punto en la gráfica de la función sinusoidal tendrá el form (\(\theta , \sin \theta\)), y cada punto en la gráfica de la función coseno tendrá el form (\(\theta , \cos \theta\)). Se acostumbra utilizar la letra griega theta\(\theta\),, como símbolo para el ángulo. Graficar puntos en el form (\(\theta , \sin \theta\)) es igual que graficar puntos en el form (\(x,y\)). A lo largo del\(x\) eje, estaremos trazando\(\theta\), y a lo largo del\(y\) eje, estaremos trazando el valor de\(\sin \theta\). Las gráficas que dibujaremos usarán valores de\(\theta\) en radianes. Antes de dibujar las gráficas, será útil encontrar algunos valores de\(\sin \theta\) y\(\cos \theta\), para luego reunirlos en una tabla.
Revisemos las definiciones generales de estas funciones. Dado cualquier ángulo\(\theta\), dibuje en posición estándar junto con un círculo unitario. El lado terminal cruzará el círculo en algún punto (\(x,y\)), como se muestra a continuación.
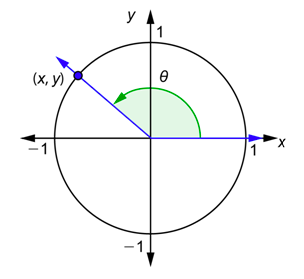
El valor de se\(\cos \theta\) ha definido como la\(x\) coordenada de este punto, y el valor de se\(\sin \theta\) ha definido como la\(y\) coordenada de este punto.
Problema: Encontrar los valores de\(\sin \theta\) y\(\cos \theta\) para\(\theta=\frac{\pi}{6}, \frac{5 \pi}{6}, \frac{7 \pi}{6}\), y\(\frac{11\pi}{6}\).
Responder
Podría resultarte útil convertir estos ángulos a grados. Los cuatro ángulos tienen un ángulo de referencia\(30^{\circ}\) o\(\frac{\pi}{6}\) radianes.
\ (\ begin {alineado}
\ frac {\ pi} {6} &=30^ {\ circ}\
\ frac {5\ pi} {6} &=150^ {\ circ}\
\ frac {7\ pi} {6} &=210^ {\ circ}\
\ frac {11\ pi} {6} &=330^ {\ circ} final
\ {alineado}\)
Usa la definición de triángulo rectángulo para encontrar el\(\sin \theta\) y\(\cos \theta\) para\(\theta=\frac{\pi}{6}\).
\ (\ begin {array} {c}
\ frac {\ cos\ pi} {6} =\ cos 30^ {\ circ} =\ frac {\ sqrt {3}} {2}\
\ frac {\ sin\ pi} {6} =\ sin 30^ {\ circ} =\ frac {1} {2}
\ end {array}\)
Grafica los cuatro ángulos en posición estándar. Las coordenadas del punto en el primer cuadrante se encontraron arriba. La\(x\) coordenada -es el valor de\(\cos \theta\), y la\(y\) coordenada -es el valor de\(\sin \theta\). Los otros puntos son reflexiones del primer punto sobre el\(x\) eje -axis, el\(y\) -axis, o ambos.
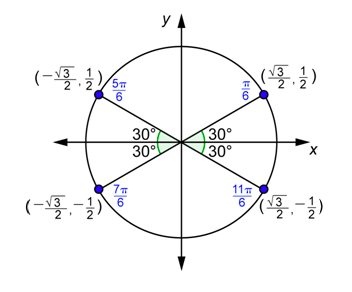
\ (\ begin {array} {l}
\ cos\ izquierda (\ frac {\ pi} {6}\ derecha) =\ cos\ izquierda (\ frac {11\ pi} {6}\ derecha) =\ frac {\ sqrt {3}} {2}\\ cos\ izquierda (\ frac {5\
pi} {6}\ derecha) =\ cos\ izquierda (\ frac {5\ pi} {6}\ derecha) =\ cos\ izquierda (\ frac {5\ pi} {6}\ derecha) =\ 7\ pi} {6}\ derecha) =-\ frac {
\ sqrt {3}} {2}\\\ sin\ izquierda (\ frac {\ pi} {6}\ derecha) =\ sin\ izquierda (\ frac {5\ pi} {6}\ derecha) =\ frac {1} {2},\ sin\ izquierda (\ frac {7\ pi} {6}\ derecha) =\ sin\ izquierda (\ frac {11\ pi} {6}\ derecha) =-\ frac {1} {2}
\ end {array}\)
Se puede pasar por un procedimiento similar para encontrar los valores de\(\cos \theta\) y\(\sin \theta\) para\(\theta=\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \text { and } \frac{7 \pi}{4}\). Los cuatro ángulos tienen un ángulo de referencia de\(\frac{\pi}{4}\) radianes o\(45^{\circ}\).
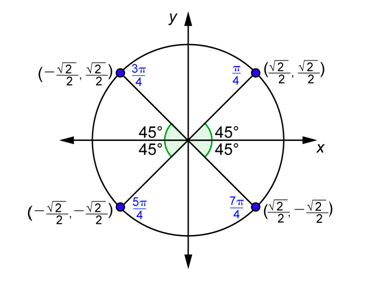
Utilizando el hecho que te\(\cos \left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}=\sin \left(\frac{\pi}{4}\right)\) da las coordenadas del punto en el primer cuadrante. Dado que los otros puntos son reflejos de éste, las coordenadas tienen los mismos valores o los valores opuestos.
El siguiente diagrama se puede utilizar para encontrar los valores de\(cos \theta\) y\(sin \theta\) para\(\theta=0, \frac{\pi}{2}, \pi, \frac{3 \pi}{2}, \text { and } 2 \pi\). Tenga en cuenta que porque\(2 \pi=360^{\circ}\), cuando dibuja el ángulo\(2\pi\) en posición estándar, termina de nuevo en el\(x\) eje -axis. \(2\pi\)radianes o\(360^{\circ}\) corresponde al mismo punto que 0 radianes, es decir, (1,0).
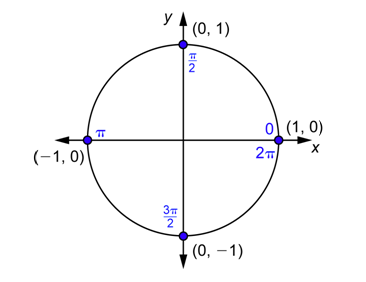
El uso de las coordenadas de los cuatro puntos te da:
\ (\ begin {array} {cc}
\ cos 0=\ cos 2\ pi=1 &\ sin\ izquierda (\ frac {\ pi} {2}\ derecha) =1\
\ cos\ izquierda (\ frac {\ pi} {2}\ derecha) =\ cos\ izquierda (\ frac {3\ pi} {2}\ derecha) =0 &\ sin 0=\ sin\ pi= 2\ pi=0\\
\ cos\ pi=-1 &\ sin\ izquierda (\ frac {3\ pi} {2}\ derecha) =-1
\ end {array }\)
Actividad Interactiva Suplementaria
Para familiarizarse más con las coordenadas de los puntos en el círculo unitario, pruebe el siguiente ejercicio interactivo.
*Insertar módulo de actividad interactiva
La Gráfica de la Función Sinusoidal
Nuestro objetivo en estos momentos es graficar la función\(y = \sin \theta\). Cada punto en la gráfica de esta función tendrá la forma (\(\theta, \sin \theta\)) con los valores de\(\theta\) en radianes. El primer paso es reunir en una tabla todos los valores de lo\(\sin \theta\) que conoces. Para comenzar, usaremos valores de\(\theta\) entre\(0^{\circ}\) y\(180^{\circ}\) (o\(0 \leq \theta \leq \pi\)).
| \(\theta\)(en grados) | \(\theta\)(en radianes) | \(\sin \theta\) | (\(\theta, \sin \theta\)) |
|---|---|---|---|
| \ (\ theta\) (en grados) “>\(0^{\circ}\) | \ (\ theta\) (en radianes) ">0 | \ (\ sin\ theta\) ">0 | \ (\ theta,\ sin\ theta\)) "> (0,0) |
| \ (\ theta\) (en grados) “>\(30^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{\pi}{6}\) | \ (\ sin\ theta\) ">\(\frac{1}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{6}\),\(\frac{1}{2}\)) |
| \ (\ theta\) (en grados) “>\(45^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{\pi}{4}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{2}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{4}\),\(\frac{\sqrt{2}}{2}\)) |
| \ (\ theta\) (en grados) “>\(60^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{\pi}{3}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{3}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{3}\),\(\frac{\sqrt{3}}{2}\)) |
| \ (\ theta\) (en grados) “>\(90^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{\pi}{2}\) | \ (\ sin\ theta\) ">1 | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{2}\), 1) |
| \ (\ theta\) (en grados) “>\(120^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{2\pi}{3}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{3}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{2\pi}{3}\),\(\frac{\sqrt{3}}{2}\)) |
| \ (\ theta\) (en grados) “>\(135^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{3\pi}{4}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{2}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{3\pi}{4}\),\(\frac{\sqrt{2}}{2}\)) |
| \ (\ theta\) (en grados) “>\(150^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{5\pi}{6}\) | \ (\ sin\ theta\) ">\(\frac{1}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{5\pi}{6}\),\(\frac{1}{2}\)) |
| \ (\ theta\) (en grados) “>\(180^{\circ}\) | \ (\ theta\) (en radianes) ">\(\pi\) | \ (\ sin\ theta\) ">0 | \ (\ theta,\ sin\ theta\)) "> (\(\pi\), 0) |
Cuando graficamos funciones, a menudo decimos graficar la función en un intervalo. Usamos notación de intervalo para describir el intervalo. La notación de intervalo tiene la forma [\(a,b\)], lo que significa que el intervalo comienza en\(a\) y termina en\(b\). En el ejemplo, la notación [\(0, \pi\)] tiene el mismo significado que\(0 \leq \theta \leq \pi\).
Problema: Grafica la función sinusoidal en el intervalo [\(0, \pi\)]. Describir los valores de la función como\(\theta\) va de 0 a\(\pi\).
Responder
Trazar todos los puntos de la última columna de la tabla anterior. Tenga en cuenta eso\(\frac{\sqrt{2}}{2} \approx 0.7\) y eso\(\frac{\sqrt{3}}{2} \approx 0.9\). Conecte los puntos con una curva suave.
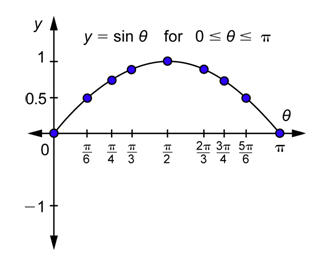
Los valores aumentan de 0 a 1 y luego disminuyen de 1 a 0.
Tenga en cuenta que nuestra entrada es\(\theta\), la medida del ángulo en radianes, y que el eje horizontal está etiquetado\(\theta\), no\(x\). A continuación reuniremos todos los valores de lo\(\sin \theta\) que conoces\(\pi \leq \theta \leq 2\pi\) en una tabla.
| \(\theta\)(en grados) | \(\theta\)(en radianes) | \(\sin \theta\) | (\(\theta, \sin \theta\)) |
|---|---|---|---|
| \ (\ theta\) (en grados) “>\(180^{\circ}\) | \ (\ theta\) (en radianes) ">\(\pi\) | \ (\ sin\ theta\) ">0 | \ (\ theta,\ sin\ theta\)) "> (\(\pi\),0) |
| \ (\ theta\) (en grados) “>\(210^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{7\pi}{6}\) | \ (\ sin\ theta\) ">\(-\frac{1}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{7\pi}{6}\),\(-\frac{1}{2}\)) |
| \ (\ theta\) (en grados) “>\(225^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{5\pi}{4}\) | \ (\ sin\ theta\) ">\(-\frac{\sqrt{2}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{5\pi}{4}\),\(-\frac{\sqrt{2}}{2}\)) |
| \ (\ theta\) (en grados) “>\(240^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{4\pi}{3}\) | \ (\ sin\ theta\) ">\(-\frac{\sqrt{3}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{4\pi}{3}\),\(-\frac{\sqrt{3}}{2}\)) |
| \ (\ theta\) (en grados) “>\(270^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{3\pi}{2}\) | \ (\ sin\ theta\) ">-1 | \ (\ theta,\ sin\ theta\)) "> (\(3\frac{\pi}{2}\), -1) |
| \ (\ theta\) (en grados) “>\(300^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{5\pi}{3}\) | \ (\ sin\ theta\) ">\(-\frac{\sqrt{3}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{5\pi}{3}\),\(-\frac{\sqrt{3}}{2}\)) |
| \ (\ theta\) (en grados) “>\(315^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{7\pi}{4}\) | \ (\ sin\ theta\) ">\(-\frac{\sqrt{2}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{7\pi}{4}\),\(-\frac{\sqrt{2}}{2}\)) |
| \ (\ theta\) (en grados) “>\(330^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{11\pi}{6}\) | \ (\ sin\ theta\) ">\(-\frac{1}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{11\pi}{6}\),\(-\frac{1}{2}\)) |
| \ (\ theta\) (en grados) “>\(360^{\circ}\) | \ (\ theta\) (en radianes) ">\(2\pi\) | \ (\ sin\ theta\) ">0 | \ (\ theta,\ sin\ theta\)) "> (\(2\pi\), 0) |
Simplemente podrías trazar todos los puntos de la última columna y continuar la gráfica en el último ejemplo. Pero fíjese lo siguiente: los valores en la tercera columna (o\(y\) -coordenadas de los puntos) tienen los valores opuestos de los puntos que acabamos de graficar. Esto significa que en lugar de trazar puntos por encima del\(\theta\) eje -eje, estarás trazando puntos debajo del\(\theta\) eje -axis. Además, las entradas y salidas están espaciadas de la misma manera para esta parte de la gráfica que para la primera parte de la gráfica. Entonces, en vez de tener un “cerro” que va de 0 hasta 1 y abajo a 0, tendrás un “valle” que baja de 0 a -1 y luego hasta 0.
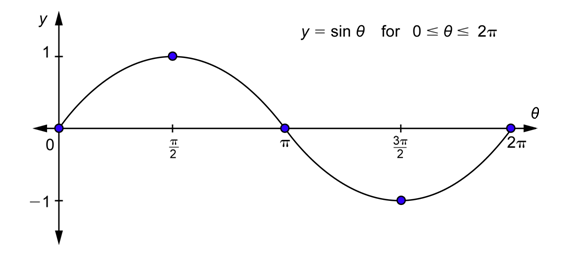
Hemos utilizado valores\(\theta\) de 0\(2\pi\) a para dibujar la gráfica de la función sinusoidal. ¿Cómo se ve la gráfica si seguimos a la derecha de\(2\pi\) for\(2\pi \leq \theta \leq 4\pi\), que es una vez más alrededor del círculo unitario? En cuanto a grados, estos son ángulos entre\(360^{\circ}\) y\(720^{\circ}\). Regresemos y veamos uno de estos ángulos en posición estándar con el círculo unitario. A continuación se muestra un\(400^{\circ}\) ángulo.
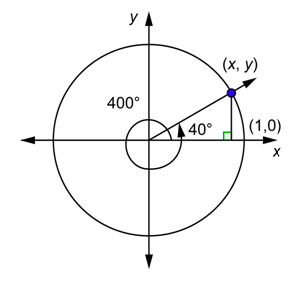
Porque\(400^{\circ}=360^{\circ}+40^{\circ}\), el ángulo recorre una rotación completa más otra\(40^{\circ}\), como lo muestra la flecha curva en el diagrama. Imagina que estás en (1,0) y caminas alrededor del círculo una vez completa y luego caminas un poco más para terminar en (\(x,y\)). Este punto donde el lado terminal se cruza con el círculo unitario es el mismo punto que obtendrías para un\(40^{\circ}\) ángulo. Todas las funciones trigonométricas para estos dos ángulos se calculan utilizando las coordenadas de este punto. Esto significa que\(\sin 400^{\circ}=\sin 40^{\circ}\),\(\cos 400^{\circ}=\cos 40^{\circ}\),\(\tan 400^{\circ}=\tan 40^{\circ}\), y lo mismo es cierto para las tres funciones recíprocas.
No hay nada de especial en\(400^{\circ}\). Podrías dibujar otros ángulos que sean mayores que\(360^{\circ}\) y encontrar resultados similares. Los resultados anteriores para seno y coseno se pueden reescribir como\(\sin \left(40^{\circ}+360^{\circ}\right)=\sin 40^{\circ}\) y\(\cos \left(40^{\circ}+360^{\circ}\right)=\cos 40^{\circ}\). En general, es cierto que\(\sin \left(\theta^{\circ}+360^{\circ}\right)=\sin \theta^{\circ}\) y\(\cos \left(\theta^{\circ}+360^{\circ}\right)=\cos \theta^{\circ}\), o, usando radianes:
\(\sin (\theta+2 \pi)=\sin \theta \quad \text { and } \quad \cos (\theta+2 \pi)=\cos \theta\)
Estas dos ecuaciones nos dicen que cuando damos la vuelta al círculo por segunda vez, vamos a obtener los mismos valores para\(\sin (\theta+2 \pi)\) como lo hicimos para\(\sin \theta\) y los mismos valores para\(\cos (\theta+2 \pi)\) como lo hicimos para\(\cos \theta\). Es decir, a medida que recorremos el mismo círculo por segunda vez, en las mismas ubicaciones del círculo obtendremos los mismos valores para la\(y\) coordenada y la\(x\) coordenada que hicimos la primera vez alrededor del círculo.
Problema: Esboza la gráfica de la función sinusoidal en el intervalo [\(0, 4\pi\)] y encuentra el rango.
Responder
Debido a que los valores de la función seno entre\(2\pi\) y\(4\pi\) son los mismos que los valores entre 0 y\(2\pi\), la forma de la gráfica entre\(2\pi\) y\(4\pi\) es la misma que la forma de la gráfica entre 0 y\(2\pi\).
El rango es el conjunto de todos los\(y\) -valores que puede tener la función, por lo que el rango de\(y = \sin \theta\) es\(-1 \leq y \leq 1\).
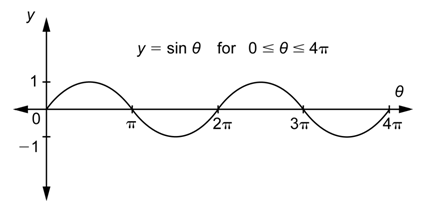
El rango de\(y = \sin \theta\) es\(-1 \leq y \leq 1\).
El mismo razonamiento que usamos anteriormente funciona para ángulos negativos. Por ejemplo, los ángulos\(-225^{\circ}\) y\(135^{\circ}\) se dibujan en posición estándar con el círculo unitario debajo.
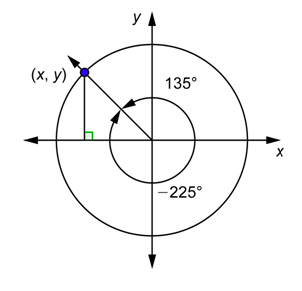
Debido a que son ángulos coterminales, intersectan el círculo unitario en el mismo punto y por lo tanto tienen las mismas coordenadas. Por lo tanto\(\sin \left(-225^{\circ}\right)=\sin 135^{\circ}\),\(\cos \left(-225^{\circ}\right)=\cos 135^{\circ}\), y así sucesivamente para las demás funciones trigonométricas. Observe que podríamos reescribir la primera ecuación como\(\sin \left(-225^{\circ}\right)=\sin \left(-225^{\circ}+360^{\circ}\right)\). Del mismo modo\(\sin \theta=\sin \left(\theta+360^{\circ}\right)\), o\(\sin \theta=\sin (\theta+2 \pi)\), es cierto para cualquier ángulo\(\theta\) incluyendo ángulos negativos. La ecuación nos\(\sin \theta=\sin (\theta+2 \pi)\) dice que cada vez que vamos una revolución completa adicional alrededor del círculo, obtenemos los mismos valores para el seno y el coseno que hicimos la primera vez alrededor del círculo.
Problema: Dibuje la gráfica de la función sinusoidal en el intervalo [\(-2\pi, 2\pi\)].
Responder
Debido a que\(\sin \theta=\sin (\theta+2 \pi)\) es cierto tanto para ángulos negativos como para ángulos positivos, los valores de la función sinusoidal entre\(-2\pi\) y 0 son los mismos que los valores de la función sinusoidal entre 0 y\(2\pi\).
Por lo tanto, la forma de la gráfica entre\(-2\pi\) y 0 es la misma que la forma de la gráfica entre 0 y\(2\pi\).
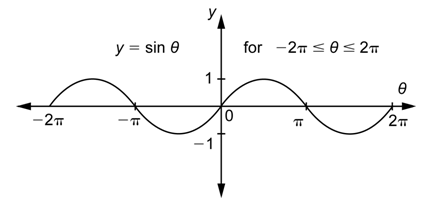
Dado que la ecuación\(\sin (\theta+2 \pi)=\sin \theta\) es cierta para cualquier ángulo, es una identidad. Podemos usar esta identidad para continuar la gráfica de la función sinusoidal en cualquier dirección. Este patrón de “colina y valle” a lo largo de un intervalo de longitud\(2\pi\) continuará en ambas direcciones para siempre.
Cada vez que añadimos\(2\pi\) a un ángulo, digamos\(\frac{\pi}{6}\) o\(30^{\circ}\), obtendremos el mismo valor de función.
\(\sin \left(\frac{\pi}{6}\right)=\sin \left(\frac{\pi}{6}+2 \pi\right)=\sin \left(\frac{\pi}{6}+4 \pi\right)=\sin \left(\frac{\pi}{6}+6 \pi\right)=\ldots=\frac{1}{2}\)
También puede usar la identidad anterior para simplificar los cálculos de la función sinusoidal restando repetidamente\(2\pi\) del ángulo. Por ejemplo:
\(\sin \left(\frac{17 \pi}{4}\right)=\sin \left(4 \pi+\frac{\pi}{4}\right)=\sin \left(2 \pi+\frac{\pi}{4}\right)=\sin \left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)
¿Cuál es el valor de\(\sin \left(\frac{25 \pi}{6}\right)\)?
- \(\frac{1}{2}\)
- \(-\frac{1}{2}\)
- \(\frac{\sqrt{3}}{2}\)
- \(-\frac{\sqrt{3}}{2}\)
- Responder
-
- \(\frac{1}{2}\). Correcto. Reescribir\(\frac{25 \pi}{6}\) como\(4 \pi+\frac{\pi}{6}\). El\(4\pi\) representa haber dado la vuelta al círculo dos veces. Usando la identidad\(\sin (\theta+2 \pi)=\sin \theta\) para eliminar una revolución a la vez, obtenemos\(\sin \left(4 \pi+\frac{\pi}{6}\right)=\sin \left(2 \pi+\frac{\pi}{6}\right)=\sin \left(\frac{\pi}{6}\right)=\sin 30^{\circ}=\frac{1}{2}\).
- \(-\frac{1}{2}\). Incorrecto. Quizás simplificaste incorrectamente y pensaste que esto era igual a\(\sin \left(\frac{7 \pi}{6}\right)\). Usa la identidad\(\sin (\theta+2 \pi)=\sin \theta\) para simplificar\(\sin \left(4 \pi+\frac{\pi}{6}\right)\). La respuesta correcta es\(\frac{1}{2}\).
- \(\frac{\sqrt{3}}{2}\). Incorrecto. Es posible que haya convertido incorrectamente de grados a radianes o confuso seno y coseno. Usa la identidad\(\sin (\theta+2 \pi)=\sin \theta\) para simplificar\(\sin \left(4 \pi+\frac{\pi}{6}\right)\). Recuerda eso\(\frac{\pi}{6} \text { radians }=30^{\circ}\). La respuesta correcta es\(\frac{1}{2}\).
- \(-\frac{\sqrt{3}}{2}\). Incorrecto. Es posible que hayas simplificado incorrectamente y pensaste que esto era igual a\(\sin \left(\frac{4 \pi}{3}\right)\). Usa la identidad\(\sin (\theta+2 \pi)=\sin \theta\) para simplificar\(\sin \left(4 \pi+\frac{\pi}{6}\right)\). La respuesta correcta es\(\frac{1}{2}\).
La Gráfica de la Función del Coseno
Ahora nuestro objetivo es graficar\(y = \cos \theta\). Pasaremos por el mismo procedimiento que hicimos para la función sinusoidal, y el resultado será similar.
Cada punto en la gráfica de la función tendrá la forma (\(\theta, \cos \theta\)) con los valores de\(\theta\) en radianes. El primer paso es reunir en una tabla todos los valores de lo\(\cos \theta\) que conoces. Para comenzar, usaremos valores de\(\theta\) entre\(0^{\circ}\) y\(180^{\circ}\) (o\(0 \leq \theta \leq \pi\)).
| \(\theta\)(en grados) | \(\theta\)(en radianes) | \(\sin \theta\) | (\(\theta, \sin \theta\)) |
|---|---|---|---|
| \ (\ theta\) (en grados) “>\(0^{\circ}\) | \ (\ theta\) (en radianes) ">0 | \ (\ sin\ theta\) ">1 | \ (\ theta,\ sin\ theta\)) "> (0,1) |
| \ (\ theta\) (en grados) “>\(30^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{\pi}{6}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{3}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{6}\),\(\frac{\sqrt{3}}{2}\)) |
| \ (\ theta\) (en grados) “>\(45^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{\pi}{4}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{2}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{4}\),\(\frac{\sqrt{2}}{2}\)) |
| \ (\ theta\) (en grados) “>\(60^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{\pi}{3}\) | \ (\ sin\ theta\) ">\(\frac{1}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{3}\),\(\frac{1}{2}\)) |
| \ (\ theta\) (en grados) “>\(90^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{\pi}{2}\) | \ (\ sin\ theta\) ">0 | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{2}\), 0) |
| \ (\ theta\) (en grados) “>\(120^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{2\pi}{3}\) | \ (\ sin\ theta\) ">\(-\frac{1}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{2\pi}{3}\),\(-\frac{1}{2}\)) |
| \ (\ theta\) (en grados) “>\(135^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{3\pi}{4}\) | \ (\ sin\ theta\) ">\(-\frac{\sqrt{2}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{3\pi}{4}\),\(-\frac{\sqrt{2}}{2}\)) |
| \ (\ theta\) (en grados) “>\(150^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{5\pi}{6}\) | \ (\ sin\ theta\) ">\(-\frac{\sqrt{3}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{5\pi}{6}\),\(-\frac{\sqrt{3}}{2}\)) |
| \ (\ theta\) (en grados) “>\(180^{\circ}\) | \ (\ theta\) (en radianes) ">\(\pi\) | \ (\ sin\ theta\) ">-1 | \ (\ theta,\ sin\ theta\)) "> (\(\pi\), -1) |
Problema: Grafica la función coseno en el intervalo [\(0, \pi\)]. Describir los valores de la función como\(\theta\) va de 0 a\(\pi\).
Responder
Trazar todos los puntos de la última columna de la tabla anterior. Tenga en cuenta eso\(\frac{\sqrt{2}}{2} \approx 0.7\) y eso\(\frac{\sqrt{3}}{2} \approx 0.9\). Conéctelos con una curva suave.
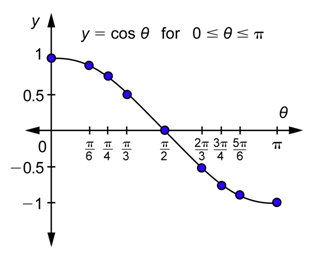
Los valores disminuyen de 1 a 0 y también continúan disminuyendo de 0 a -1.
Una vez más, nuestra entrada es\(\theta\), la medida del ángulo en radianes, y el eje horizontal está etiquetado\(\theta\), no\(x\). A continuación, reuniremos todos los valores de lo\(\cos \theta\) que conoces\(\pi \leq \theta \leq 2 \pi\) en una sola tabla.
| \(\theta\)(en grados) | \(\theta\)(en radianes) | \(\sin \theta\) | (\(\theta, \sin \theta\)) |
|---|---|---|---|
| \ (\ theta\) (en grados) “>\(180^{\circ}\) | \ (\ theta\) (en radianes) ">\(\pi\) | \ (\ sin\ theta\) ">-1 | \ (\ theta,\ sin\ theta\)) "> (0, -1) |
| \ (\ theta\) (en grados) “>\(210^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{7\pi}{6}\) | \ (\ sin\ theta\) ">\(-\frac{\sqrt{3}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{6}\),\(-\frac{\sqrt{3}}{2}\)) |
| \ (\ theta\) (en grados) “>\(225^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{5\pi}{4}\) | \ (\ sin\ theta\) ">\(-\frac{\sqrt{2}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{4}\),\(-\frac{\sqrt{2}}{2}\)) |
| \ (\ theta\) (en grados) “>\(240^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{4\pi}{3}\) | \ (\ sin\ theta\) ">\(-\frac{1}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{3}\),\(-\frac{1}{2}\)) |
| \ (\ theta\) (en grados) “>\(270^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{3\pi}{2}\) | \ (\ sin\ theta\) ">0 | \ (\ theta,\ sin\ theta\)) "> (\(\frac{\pi}{2}\), 0) |
| \ (\ theta\) (en grados) “>\(300^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{5\pi}{3}\) | \ (\ sin\ theta\) ">\(\frac{1}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{2\pi}{3}\),\(\frac{1}{2}\)) |
| \ (\ theta\) (en grados) “>\(315^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{7\pi}{4}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{2}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{3\pi}{4}\),\(\frac{\sqrt{2}}{2}\)) |
| \ (\ theta\) (en grados) “>\(330^{\circ}\) | \ (\ theta\) (en radianes) ">\(\frac{11\pi}{6}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{3}}{2}\) | \ (\ theta,\ sin\ theta\)) "> (\(\frac{5\pi}{6}\),\(\frac{\sqrt{3}}{2}\)) |
| \ (\ theta\) (en grados) “>\(360^{\circ}\) | \ (\ theta\) (en radianes) ">\(2\pi\) | \ (\ sin\ theta\) ">1 | \ (\ theta,\ sin\ theta\)) "> (\(\pi\), 1) |
Nuevamente, podrías simplemente trazar todos los puntos de la última columna y continuar con la gráfica. En cambio, compare los valores en las terceras columnas de las dos tablas: son los mismos números, pero en el orden inverso. Estas son las\(y\) coordenadas 1 de los puntos. Esto significa que mientras la primera parte que graficamos disminuyó de 1 a -1, esta segunda parte que estamos graficando aumentará de -1 a 1 y tendrá la “misma forma” (girada al revés). Aquí está:
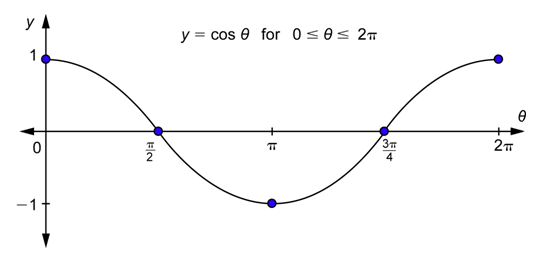
El siguiente paso es continuar con la gráfica para los valores de entrada\(2\pi \leq \theta \leq 4 \pi\). Cuando estábamos en el proceso de graficar la función sinusoidal, establecimos la siguiente identidad:
\(\cos (\theta+2 \pi)=\cos \theta\)
Esta ecuación nos dice que cuando damos la vuelta al círculo por segunda vez, vamos a obtener los mismos valores para que\(\cos (\theta+2 \pi)\) lo hicimos para\(\cos \theta\).
Es decir, a medida que vamos dando la vuelta al mismo círculo por segunda vez, en las mismas ubicaciones del círculo obtendremos los mismos valores para la\(x\) coordenada -que hicimos la primera vez alrededor del círculo.
Problema: Esbozar la gráfica de la función coseno en el intervalo [\(0, 4\pi\)].
Responder
Debido a que las salidas entre\(2\pi\) y\(4\pi\) son las mismas que las salidas entre 0 y\(2\pi\), la forma de la gráfica entre\(2\pi\) y\(4\pi\) es la misma que la forma de la gráfica entre 0 y\(2\pi\).
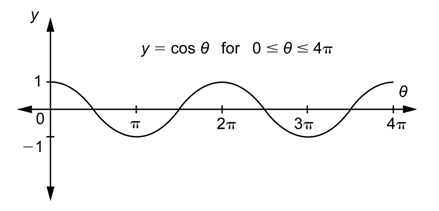
Así como la identidad\(\sin \theta=\sin (\theta+2 \pi)\) es cierta para los ángulos negativos, la identidad también\(\cos (\theta+2 \pi)=\cos \theta\) es cierta para cualquier ángulo negativo\(\theta\).
Problema: Esbozar la gráfica de la función coseno en el intervalo [\(-2\pi, 2\pi\)].
Responder
Debido a que\(\cos \theta=\cos (\theta+2 \pi)\) es cierto tanto para ángulos negativos como para ángulos positivos, los valores de la función coseno entre\(-2\pi\) y 0 son los mismos que los valores de la función coseno entre 0 y\(2\pi\).
Por lo tanto, la forma de la gráfica entre\(-2\pi\) y 0 es la misma que la forma de la gráfica entre 0 y\(2\pi\).
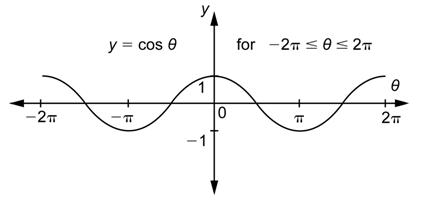
La identidad\(\cos (\theta+2 \pi)=\cos \theta\) se utilizó anteriormente para extender la gráfica de la función coseno hacia la derecha y hacia la izquierda. Puedes usar esto para continuar extendiendo la gráfica en ambas direcciones. Obtendrás otro patrón de “colina y valle” que se repite después de intervalos de longitud\(2\pi\) en ambas direcciones.
Otra característica importante de la gráfica de\(y = \cos \theta\) es que las mitades izquierda y derecha son imágenes especular entre sí sobre el\(y\) eje -eje. La gráfica de\(y = x^2\) tiene esta misma propiedad. Otra forma de describir esto es decir que si sustitues un número y su opuesto en la función, obtendrá el mismo valor que la ecuación anterior. Por ejemplo,\(\cos \left(-\frac{\pi}{4}\right)=\cos \left(\frac{\pi}{4}\right)\),\(\cos (-\pi)=\cos \pi\), o en general,\(\cos (-\theta)=\cos \theta\). Decimos que la gráfica es simétrica alrededor del eje y. El siguiente diagrama muestra dos puntos tomados de una gráfica simétrica.
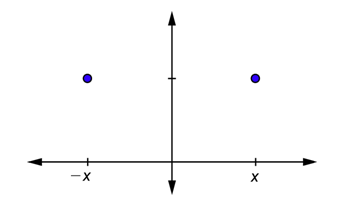
La altura de los puntos en entradas opuestas es la misma. La altura es el valor de la función. Una función cuya gráfica es simétrica alrededor del\(y\) eje -tiene\(f(-x)=f(x)\).
¿Cuál es el rango de la función coseno?
- todos los valores en el intervalo [0,1]
- todos los valores en el intervalo [-1,1]
- todos los valores en el intervalo [0,\(2\pi\)]
- todos los números reales
- Responder
-
- todos los valores en el intervalo [0,1]. Incorrecto. Probablemente estabas mirando los\(y\) -valores, que es lo correcto que hay que hacer. Sin embargo, elegiste solo una parte de la gama. El rango es el conjunto de todos los\(y\) -valores que puede tener la función; en este caso eso sería\(-1 \leq y \leq 1\). La respuesta correcta es B.
- todos los valores en el intervalo [-1,1]. Correcto. La gráfica de la función se extiende para siempre en ambas direcciones, por lo que su dominio es todo números reales. Consiste en un patrón repetitivo de colinas y valles. El valle baja a un\(y\) -valor de -1, y el cerro sube a un\(y\) -valor de 1. Todos los\(y\) valores -entre estos dos\(y\) -valores también son salidas de la función. Entonces el conjunto de salidas, o rango, son todos los números de -1 a 1.
- todos los valores en el intervalo [0,\(2\pi\)]. Incorrecto. Este intervalo, como conjunto de entradas, te dará un patrón completo. Es el conjunto de salidas que buscas. La respuesta correcta es B.
- todos los números reales. Incorrecto. Quizás estabas pensando en el dominio de la función, que es todo números reales. El rango es el conjunto de todas las salidas o\(y\) -valores. La respuesta correcta es B.
Una comparación de las gráficas de seno y coseno
Las gráficas de seno y coseno tienen colinas y valles en un patrón repetitivo.
Dado que este patrón de repetición se puede extender indefinidamente a la izquierda y a la derecha, el dominio para ambas funciones son los números reales. El rango para ambos es el intervalo [-1,1].
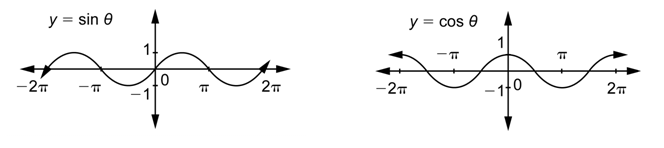
Ahora comparemos estas gráficas de otras maneras.
Primero, queremos ver qué sucede con la gráfica de una función cuando cambias la entrada agregándole una constante. Comparar\(y = \sin \theta\) y\(y=\sin \left(\theta+\frac{\pi}{2}\right)\). Aquí hay una tabla con algunos valores para estas dos funciones.
| \(\theta\)(en radianes) | \(\sin \theta\) | \(\theta + \frac{\pi}{2}\)(en radianes) | \(\sin \left(\theta+\frac{\pi}{2}\right)\) |
|---|---|---|---|
| \ (\ theta\) (en radianes) ">0 | \ (\ sin\ theta\) ">0 | \ (\ theta +\ frac {\ pi} {2}\) (en radianes) ">\(\frac{\pi}{2}\) | \ (\ sin\ izquierda (\ theta+\ frac {\ pi} {2}\ derecha)\) ">1 |
| \ (\ theta\) (en radianes) ">\(\frac{\pi}{6}\) | \ (\ sin\ theta\) ">\(\frac{1}{2}\) | \ (\ theta +\ frac {\ pi} {2}\) (en radianes) ">\(\frac{2\pi}{3}\) | \ (\ sin\ izquierda (\ theta+\ frac {\ pi} {2}\ derecha)\) ">\(\frac{\sqrt{3}}{2}\) |
| \ (\ theta\) (en radianes) ">\(\frac{\pi}{4}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{2}}{2}\) | \ (\ theta +\ frac {\ pi} {2}\) (en radianes) ">\(\frac{3\pi}{4}\) | \ (\ sin\ izquierda (\ theta+\ frac {\ pi} {2}\ derecha)\) ">\(\frac{\sqrt{2}}{2}\) |
| \ (\ theta\) (en radianes) ">\(\frac{\pi}{3}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{3}}{2}\) | \ (\ theta +\ frac {\ pi} {2}\) (en radianes) ">\(\frac{5\pi}{6}\) | \ (\ sin\ izquierda (\ theta+\ frac {\ pi} {2}\ derecha)\) ">\(\frac{1}{2}\) |
| \ (\ theta\) (en radianes) ">\(\frac{\pi}{2}\) | \ (\ sin\ theta\) ">1 | \ (\ theta +\ frac {\ pi} {2}\) (en radianes) ">\(\pi\) | \ (\ sin\ izquierda (\ theta+\ frac {\ pi} {2}\ derecha)\) ">0 |
| \ (\ theta\) (en radianes) ">\(\frac{2\pi}{3}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{3}}{2}\) | \ (\ theta +\ frac {\ pi} {2}\) (en radianes) ">\(\frac{7\pi}{6}\) | \ (\ sin\ izquierda (\ theta+\ frac {\ pi} {2}\ derecha)\) ">\(-\frac{1}{2}\) |
| \ (\ theta\) (en radianes) ">\(\frac{3\pi}{4}\) | \ (\ sin\ theta\) ">\(\frac{\sqrt{2}}{2}\) | \ (\ theta +\ frac {\ pi} {2}\) (en radianes) ">\(\frac{5\pi}{4}\) | \ (\ sin\ izquierda (\ theta+\ frac {\ pi} {2}\ derecha)\) ">\(-\frac{\sqrt{2}}{2}\) |
| \ (\ theta\) (en radianes) ">\(\frac{5\pi}{6}\) | \ (\ sin\ theta\) ">\(\frac{1}{2}\) | \ (\ theta +\ frac {\ pi} {2}\) (en radianes) ">\(\frac{4\pi}{3}\) | \ (\ sin\ izquierda (\ theta+\ frac {\ pi} {2}\ derecha)\) ">\(-\frac{\sqrt{3}}{2}\) |
| \ (\ theta\) (en radianes) ">\(\pi\) | \ (\ sin\ theta\) ">0 | \ (\ theta +\ frac {\ pi} {2}\) (en radianes) ">\(\frac{3\pi}{2}\) | \ (\ sin\ izquierda (\ theta+\ frac {\ pi} {2}\ derecha)\) ">-1 |
Ahora vamos a graficar estas dos funciones. Como recordatorio, la entrada es\(\theta\) para ambas funciones. Para graficar\(y = \sin \theta\), usa los números en la primera y segunda columnas. Para graficar\(y=\sin \left(\theta+\frac{\pi}{2}\right)\), usa los números en la primera y cuarta columnas. (La tercera columna se acaba de escribir como un paso intermedio conveniente. No se usa eso para la gráfica.)
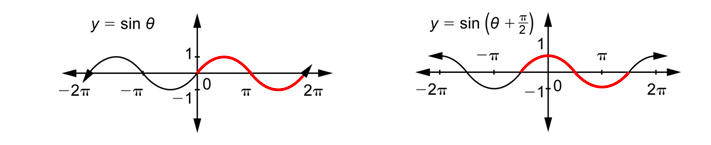
Primero observe, como muestran las piezas en rojo, que el efecto de\(\frac{\pi}{2}\) sumar a la entrada es desplazar la gráfica hacia la izquierda por\(\frac{\pi}{2}\) unidades. Tal vez recuerdes haber visto este efecto cuando graficaste funciones radicales como\(y = \sqrt{x}\) y\(y = \sqrt{x+1}\) (agregar el 1 a la entrada desplazó la gráfica de\(y = \sqrt{x}\) a la izquierda 1 unidad). En general, si agregas una constante positiva\(c\) a la entrada de una función, eso tendrá el efecto de desplazar la gráfica original hacia la izquierda por\(c\) unidades. Si restas una constante positiva de la entrada de una función, eso tendrá el efecto de desplazar la gráfica original hacia la derecha por\(c\) unidades.
A continuación, observe que la gráfica de la derecha ya le resulta familiar. Es la gráfica de\(y=\cos \theta\)! Entonces se puede decir que la gráfica de\(y=\sin \left(\theta+\frac{\pi}{2}\right)\) es la misma que la gráfica de\(y=\cos \theta\), o se puede decir que la gráfica de\(y=\sin \theta\) desplazada a la izquierda por\(\frac{\pi}{2}\) unidades es la gráfica de\(y=\cos \theta\).
El siguiente ejemplo mira un cambio en la otra dirección.
Problema: Esbozar la gráfica de\(y=\cos \left(\theta-\frac{\pi}{2}\right)\) en el intervalo [\(-2\pi, 2\pi\)]. ¿Cómo se compara la gráfica con la gráfica de\(y=\sin \theta\)?
Responder
La gráfica de\(y=\cos \left(\theta-\frac{\pi}{2}\right)\) es la misma que la gráfica de\(\frac{\pi}{2}\) unidades\(y=\cos \theta\) desplazadas a la derecha.
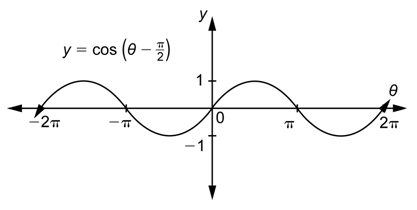
La gráfica de\(y=\cos \left(\theta-\frac{\pi}{2}\right)\) es la misma que la gráfica de\(y=\sin \theta\).
Debido a que los patrones se repiten, podrías comenzar con la gráfica de seno o coseno y desplazarla por diferentes cantidades hacia la derecha o hacia la izquierda para obtener la gráfica de la otra función.
¿Cuál comparación de las gráficas de\(y=\sin \theta\) y\(y=\cos \theta\) es cierta?
- Ellos son lo mismo.
- La gráfica de\(\frac{\pi}{2}\) unidades\(y=\sin \theta\) desplazadas a la derecha es la gráfica de\(y=\cos \theta\).
- La gráfica de\(\pi\) unidades\(y=\sin \theta\) desplazadas a la derecha es la gráfica de\(y=\cos \theta\).
- La gráfica de\(\frac{\pi}{2}\) unidades\(y=\sin \theta\) desplazadas a la izquierda es la gráfica de\(y=\cos \theta\).
- Responder
-
- Ellos son lo mismo. Incorrecto. Las dos gráficas tienen el mismo patrón repetitivo o la misma forma general, pero no son idénticas. La respuesta correcta es D.
- La gráfica de\(\frac{\pi}{2}\) unidades\(y=\sin \theta\) desplazadas a la derecha es la gráfica de\(y=\cos \theta\). Incorrecto. Si cambias seno y coseno en esta opción obtienes una declaración correcta. Las dos gráficas descritas en esta opción tienen la misma forma, pero los cerros y valles no coinciden. La respuesta correcta es D.
- La gráfica de\(\pi\) unidades\(y=\sin \theta\) desplazadas a la derecha es la gráfica de\(y=\cos \theta\). Incorrecto. Si desplazas la gráfica de la función sinusoidal por\(\pi\) unidades hacia la derecha, obtienes una gráfica que “comienza” (at\(\theta = 0\)) con un valle. Esta no es la gráfica de la función coseno. La respuesta correcta es D.
- La gráfica de\(\frac{\pi}{2}\) unidades\(y=\sin \theta\) desplazadas a la izquierda es la gráfica de\(y=\cos \theta\). Correcto. Si desplaza la gráfica de\(y=\sin \theta\) por\(\frac{\pi}{2}\) unidades hacia la izquierda, obtendrá una gráfica que “comienza” (a\(\theta = 0\)) en la cima de una colina. Esta es la gráfica de\(y=\cos \theta\).
Actividad Interactiva Suplementaria
Para practicar graficar seno y coseno, prueba el siguiente ejercicio interactivo.
*Insertar módulo de actividad interactiva
Resumen
Las gráficas de seno y coseno tienen la misma forma: un patrón repetitivo de “colina y valle” a lo largo de un intervalo en el eje horizontal que tiene una longitud de\(2\pi\). Las funciones seno y coseno tienen el mismo dominio, los números reales, y el mismo rango, el intervalo de valores [-1,1].
Las gráficas de las dos funciones, aunque similares, no son idénticas. Una forma de describir su relación es decir que la gráfica de\(y=\cos \theta\) es idéntica a la gráfica de\(\frac{\pi}{2}\) unidades\(y=\sin \theta\) desplazadas a la izquierda. Otra forma de describir su relación es decir que la gráfica de\(y=\sin \theta\) es idéntica a la gráfica de\(\frac{\pi}{2}\) unidades\(y=\cos \theta\) desplazadas a la derecha.


