6.4: Circuitos Hamiltonianos
- Page ID
- 109948
El problema del vendedor ambulante (TSP) es cualquier problema en el que debes visitar cada vértice de una gráfica ponderada una vez y solo una vez, y luego terminar de nuevo en el vértice inicial. Ejemplos de situaciones de TSP son entregas de paquetes, fabricación de placas de circuitos, programación de trabajos en una máquina y hacer recados por la ciudad.
| Circuito Hamilton: un circuito que debe pasar por cada vértice de una gráfica una y sólo una vez |
| Camino de Hamilton: un camino que debe pasar por cada vértice de una gráfica una y sólo una vez |
Ejemplo\(\PageIndex{1}\): Camino de Hamilton:
| a. |
b. |
c. |
Figura\(\PageIndex{1}\): Ejemplos de Hamilton Paths
No todas las gráficas tienen un circuito o trayectoria de Hamilton. No hay manera de saber con solo mirar una gráfica si tiene un circuito o camino de Hamilton como se puede con un circuito o camino de Euler. Debe hacer prueba y error para determinar esto. Por cierto si una gráfica tiene un circuito de Hamilton entonces tiene un camino Hamilton. Simplemente no vuelvas a casa.
La gráfica a. tiene un circuito Hamilton (un ejemplo es ACDBEA)
El gráfico b. no tiene circuitos Hamilton, aunque tiene una ruta Hamilton (un ejemplo es ABCDEJGIFH)
El gráfico c. tiene un circuito Hamilton (un ejemplo es AGFECDBA)
| Gráfica completa: Una gráfica completa es una gráfica con N vértices en la que cada par de vértices se une exactamente por un borde. El símbolo utilizado para denotar una gráfica completa es KN. |
Ejemplo\(\PageIndex{2}\): Gráficas Completas
| a. K\(_2\) | b. K\(_3\) | c. K\(_4\) | d. K\(_5\) |
| dos vértices y un borde | tres vértices y tres aristas | cuatro vértices y seis aristas | cinco vértices y diez aristas |
Figura\(\PageIndex{2}\): Gráficas completas para N = 2, 3, 4 y 5
En cada gráfica completa mostrada arriba, hay exactamente una arista que conecta cada par de vértices. No hay bucles o múltiples aristas en las gráficas completas. Las gráficas completas sí tienen circuitos Hamilton.
| Punto de referencia: el punto de partida de un circuito de Hamilton |
Ejemplo\(\PageIndex{3}\): Punto de referencia en una gráfica completa
Muchos circuitos de Hamilton en una gráfica completa son el mismo circuito con diferentes puntos de partida. Por ejemplo, en la gráfica K3, que se muestra a continuación en la Figura\(\PageIndex{3}\), ABCA es el mismo circuito que BCAB, solo con un punto de partida diferente (punto de referencia). Normalmente asumiremos que el punto de referencia es A.
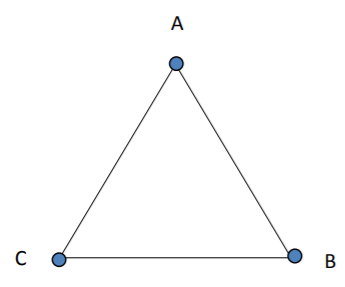
Figura\(\PageIndex{3}\): K\(_3\)
| Número de Circuitos Hamilton: ¡Una gráfica completa con N vértices es (N-1)! Circuitos Hamilton. Dado que la mitad de los circuitos son imágenes especulares de la otra mitad, en realidad solo hay la mitad de estos muchos circuitos únicos. |
Ejemplo\(\PageIndex{4}\): Número de circuitos Hamilton
¿Cuántos circuitos Hamilton tiene una gráfica con cinco vértices?
(N — 1)! = (5 — 1)! = 4! = 4*3*2*1 = 24 circuitos Hamilton.
Cómo resolver un problema de vendedor ambulante (TSP):
Un problema de vendedor ambulante es un problema en el que imaginas que un vendedor ambulante va de viaje de negocios. Comienza en su ciudad natal (A) y luego necesita viajar a varias ciudades diferentes para vender sus mercancías (las otras ciudades son B, C, D, etc.). Para resolver un TSP, necesitas encontrar la forma más barata para que el vendedor ambulante comience en casa, A, viaje a las otras ciudades, y luego regrese a casa a A al final del viaje. Esto es simplemente encontrar el circuito de Hamilton en una gráfica completa que tenga el menor peso total. Existen varios algoritmos diferentes que se pueden utilizar para resolver este tipo de problemas.
A. Algoritmo de fuerza bruta
- Enumere todos los circuitos Hamilton posibles de la gráfica.
- Para cada circuito encuentra su peso total.
- El circuito con el menor peso total es el circuito óptimo de Hamilton.
Ejemplo\(\PageIndex{5}\): Algoritmo de fuerza bruta:
Supongamos que un repartidor necesita entregar paquetes a tres ubicaciones y regresar a la oficina en casa A. Usando el gráfico que se muestra arriba en la Figura\(\PageIndex{4}\), encuentre la ruta más corta si los pesos en la gráfica representan la distancia en millas.
Recordemos la manera de saber cuántos circuitos Hamilton tiene esta gráfica completa. La gráfica completa anterior tiene cuatro vértices, por lo que el número de circuitos de Hamilton es:
(N — 1)! = (4 — 1)! = ¡3! = 3*2*1 = 6 circuitos Hamilton.
Sin embargo, tres de esos circuitos de Hamilton son el mismo circuito que va en dirección opuesta (la imagen especular).
| Circuito Hamilton | Imagen espejada | Peso Total (Millas) |
| ABCDA | ADCBA | 18 |
| ABDCA | ACDBA | 20 |
| ACBDA | ADBCA | 20 |
La solución es ABCDA (o ADCBA) con un peso total de 18 mi. Esta es la solución óptima.
B. Algoritmo del vecino más cercano:
- Elija un vértice como punto de partida.
- Desde el punto de partida ir al vértice con un borde con el menor peso. Si hay más de una opción, elija al azar.
- Continuar construyendo el circuito, un vértice a la vez de entre los vértices que aún no han sido visitados.
- Desde el último vértice, regresa al punto de partida.
Ejemplo\(\PageIndex{6}\): Algoritmo del vecino más cercano
Un repartidor necesita entregar paquetes a cuatro ubicaciones y regresar a la oficina A en casa como se muestra en la Figura\(\PageIndex{5}\) a continuación. Encuentra la ruta más corta si los pesos representan distancias en millas.
A partir de A, E es el vecino más cercano ya que tiene el menor peso, así que ve a E. De E, B es el vecino más cercano así que ve a B. De B, C es el vecino más cercano así que ve a C. De C, el primer vecino más cercano es B, pero acabas de llegar de ahí. El siguiente vecino más cercano es A, pero todavía no quieres ir allí porque ese es el punto de partida. El siguiente vecino más cercano es E, pero ya fuiste ahí. Así que ve a D. De D, vaya a A ya que todos los demás vértices han sido visitados.
La solución es AEBCDA con un peso total de 26 millas. Esta no es la solución óptima, pero está cerca y fue un método muy eficiente.
C. Algoritmo repetitivo del vecino más cercano:
- Deja que X sea cualquier vértice. Aplicar el Algoritmo de Vecino Más Cercano usando X como vértice de inicio y calcular el costo total del circuito obtenido.
- Repita el proceso usando cada uno de los otros vértices de la gráfica como vértice inicial.
- De los circuitos Hamilton obtenidos, mantén el mejor. Si hay un vértice inicial designado, reescriba este circuito con ese vértice como punto de referencia.
Ejemplo\(\PageIndex{7}\): Algoritmo repetitivo del vecino más cercano
Supongamos que un repartidor necesita entregar paquetes a cuatro ubicaciones y regresar a la oficina en casa A. Encuentra la ruta más corta si los pesos en la gráfica representan distancias en kilómetros.
A partir de A, la solución es AEBCDA con un peso total de 26 millas como encontramos en Ejemplo\(\PageIndex{6}\). Vea esta solución a continuación en la Figura\(\PageIndex{7}\).
A partir de B, la solución es BEDACB con un peso total de 20 millas.
A partir de C, la solución es CBEDAC con un peso total de 20 millas.
A partir de D, la solución es DEBCAD con un peso total de 20 millas.
A partir de E, la solución es EBCADE con un peso total de 20 millas.
Ahora, puede comparar todas las soluciones para ver cuál tiene el peso general más bajo. La solución es cualquiera de los circuitos que comienzan en B, C, D o E ya que todos tienen el mismo peso de 20 millas. Ahora que conoces la mejor solución usando este método, puedes reescribir el circuito comenzando por cualquier vértice. Dado que la oficina en casa en este ejemplo es A, reescribamos las soluciones comenzando por A. Así, la solución es ACBEDA o ADEBCA.
D. Algoritmo de enlace barato
- Escoge primero el enlace con el peso más pequeño (si hay empate, elige uno al azar). Marcar el borde correspondiente en rojo.
- Escoge el siguiente enlace más barato y marca el borde correspondiente en rojo.
- Continuar recogiendo el enlace más barato disponible. Marcar el borde correspondiente en rojo excepto cuando a) cierra un circuito o b) da como resultado que tres bordes salgan de un solo vértice.
- Cuando no haya más vértices para enlazar, cierre el circuito rojo.
Ejemplo\(\PageIndex{8}\): Algoritmo de enlace barato
Supongamos que un repartidor necesita entregar paquetes a cuatro ubicaciones y regresar a la oficina en casa A. Encuentre la ruta más corta si los pesos representan distancias en millas.
Paso 1: Encuentra el enlace más barato de la gráfica y márcala en azul. El enlace más barato es entre B y E con un peso de una milla.
Paso 2: Encuentra el siguiente enlace más barato de la gráfica y márcalo en azul. El siguiente enlace más barato es entre B y C con un peso de dos millas.
Paso 3: Encuentra el siguiente enlace más barato de la gráfica y márcalo en azul siempre que no haga un circuito o no sea un tercer borde saliendo de un solo vértice. El siguiente enlace más barato es entre D y E con un peso de tres millas.
Paso 4: Encuentra el siguiente enlace más barato de la gráfica y márcalo en azul siempre que no haga un circuito o no sea un tercer borde saliendo de un solo vértice. El siguiente enlace más barato es entre A y E con un peso de cuatro millas, pero sería un tercer borde saliendo de un solo vértice. El siguiente enlace más barato es entre A y C con un peso de cinco millas. Marcarlo en azul.
Paso 5: Como todos los vértices han sido visitados, cierra el circuito con borde DA para volver a la oficina en casa, A. Este es el único borde con el que pudimos cerrar el circuito porque AB crea tres bordes saliendo del vértice B y BD también creó tres bordes saliendo del vértice B.
La solución es ACBEDA o ADEBCA con un peso total de 20 millas.
| Algoritmo eficiente: un algoritmo para el cual el número de pasos necesarios para llevarlo a cabo crece en proporción al tamaño de la entrada al problema. |
| Algoritmo aproximado: cualquier algoritmo para el cual el número de pasos necesarios para llevarlo a cabo crece en proporción al tamaño de la entrada al problema. No existe un algoritmo conocido que sea eficiente y produzca la solución óptima. |


