3: Algunos problemas teaser
- Page ID
- 107779
Para ilustrar algunas de las formas en que podemos emplear un proceso deliberado de resolución de problemas, aplicar heurística general y mirar hacia el desarrollo de estrategias de solución, ofrezco algunos problemas teaser. Revisaremos estos problemas a lo largo del texto donde sirven como forraje para discusiones más específicas sobre estrategias de solución. Estos problemas varían en complejidad y en la mayoría de los casos son bastante abiertos. Como ya hemos comentado, estas son características de problemas reales y aunque podamos sentir un poco de ansiedad por eso, también debemos darnos cuenta de que esto presenta oportunidades para la creatividad y el ingenio.
3.1 Servidumbres de aves acuáticas
Para tener el mayor beneficio para las aves acuáticas migratorias, ¿es mejor asegurar las servidumbres que contengan muchos humedales pequeños o menos, humedales más grandes?
Una de las mayores amenazas para las poblaciones de aves acuáticas es la pérdida de hábitat. Organizaciones como Ducks Unlimited y The Nature Conservancy han abogado por la preservación y restauración de humedales en corredores migratorios clave y áreas de reproducción. Entre las estrategias que han utilizado organizaciones como esta se encuentra la adquisición de servidumbres de conservación, en donde un propietario privado de tierras acuerda limitar el desarrollo de terrenos que contengan hábitat de calidad a cambio de beneficios como asistencia a la gestión y deducciones fiscales. En la práctica, estas organizaciones no pueden aceptar todas las donaciones de servidumbre sino que necesitan priorizar aquellas que tendrán mayores beneficios a largo plazo para las aves acuáticas. Así la pregunta: si todo lo demás es igual, ¿es mejor priorizar una parcela con muchos humedales pequeños, o una parcela del mismo tamaño con menos humedales grandes (Figura 3.1)?
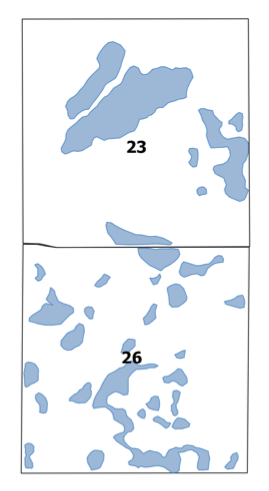
Figura 3.1: Dos tramos adyacentes, cada uno de aproximadamente 1 milla cuadrada, con diferente número y distribución de tamaño de humedales.
3.2 Compra de herbicidas
¿Cuánto herbicida se necesita para matar y suprimir el rebrote de arbustos leñosos invasores en un parque urbano arbolado?
Un problema común de manejo en los bosques urbanos es el control de la vegetación invasora o no deseada del sotobosque. En el medio oeste de Estados Unidos, las madreselvas arbustivas (género Lonicera) y la espina común europea (género Rhamnus) son particularmente difíciles de manejar, y el medio de control más efectivo suele ser con herbicida. El enfoque más simple para muchos de estos invasivos leñosos es cortar todos los tallos y pintar tocones con un herbicida general como el glifosato. Entonces, ¿qué debemos saber y determinar para decidir la cantidad de glifosato requerida?
3.3 Colisiones de ciervos y automóviles
¿Qué tan probables son las colisiones entre automóviles y venados cola blanca en su condado y cómo podrían verse influenciados por los cambios en el manejo de la población de ciervos?
Si vives en un entorno urbano sin espacios abiertos y corredores de vida silvestre, la respuesta a esto puede ser fácil: probabilidad cero. Pero en muchas zonas tanto periurbanas como rurales, los venados son un espectáculo familiar. En estos entornos, las colisiones de ciervos y automóviles pueden ser, lamentablemente, demasiado comunes. Podríamos inferir que la frecuencia de colisiones sería mayor donde tanto los ciervos como los conductores son más numerosos, pero ¿podemos cuantificar esto?
3.4 Plaga de perro pradera
¿Es posible evitar la propagación de la peste silvestre a través de las colonias de perros de la pradera?
Yersinia pestis es una bacteria transmitida por pulgas que causa la peste Silvática, una enfermedad a menudo mortal que afecta principalmente a los roedores. El perro de la pradera de cola negra (Cynomys ludivicianus), ya amenazado por el cambio de uso del suelo y la caza/envenenamiento dentro de su área de distribución nativa en las Grandes Llanuras de América del Norte, experimenta periódicamente epidemias de peste que pueden diezmar colonias. Sin embargo, además de dañar directamente a los perros de las praderas, la peste puede transmitirse tanto directamente como a través de las pulgas desde los perros de la pradera hasta sus depredadores, incluido el hurón de patas negras En poblaciones aisladas de perros de pradera, el monitoreo y el manejo activo pueden usarse potencialmente para reducir la propagación de la peste, pero diseñar una estrategia de este tipo requiere que primero entendamos la dinámica de transmisión de enfermedades dentro de las colonias.
3.5 Pérdidas por incendios forestales
¿Cuánto manejo de combustible es óptimo para minimizar el riesgo de daños por incendio en un bosque manejado para la producción maderera?
En muchos bosques occidentales gestionados para la producción maderera, la exclusión histórica de incendios ha llevado a una acumulación de leña, lo que ha llevado a un mayor riesgo de incendio destructivo. Cuando ocurren incendios en estos entornos, la alta densidad de combustible puede conducir a incendios destructivos de corona que disminuyen en gran medida el valor de la madera y pueden dañar o destruir la infraestructura circundante. Para combatir esto, los administradores forestales pueden emprender tratamientos de reducción de combustible como el adelgazamiento y la quema prescrita, y los administradores de emergencias pueden combatir agresivamente los incendios cuando inician. Sin embargo, tales esfuerzos de supresión y presupresión pueden ser costosos y pueden tener rendimientos decrecientes en términos de costo y refuentes (Figura 3.2). ¿Existe una cantidad óptima de reducción y supresión de combustible que brinde cierta protección contra el riesgo al tiempo que contiene costos?
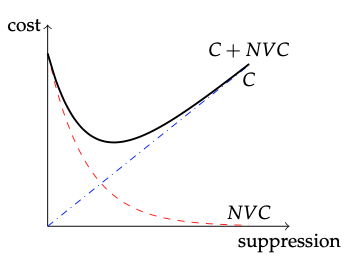
Figura 3.2: Ilustración esquemática de un modelo conceptual para el manejo óptimo de combustibles contra incendios. El costo total
C de la administración aumenta con el esfuerzo de supresión y presupresión. Sin embargo, con poco esfuerzo de supresión, el riesgo de altas pérdidas o cambio neto en el valor, NVC, es alto, disminuyendo con el esfuerzo de supresión. Esta visión de los incentivos de gestión indica que el costo general es de C + NVC.
\(^{1}\)Inspirado por Litwack et al., 2006, Journal of Environmental Engineering, 132 (4): 538-546.
3.6 Efluente maximizado
¿Qué cantidad de fósforo (P) se puede descargar de fuentes puntuales a una corriente urbana sin exceder las cargas máximas diarias totales (TMDL)? \(^{1}\)
La Ley de Agua Limpia de Estados Unidos de 1972 establece criterios para identificar cuerpos de agua contaminados y diseñar planes para reducir las cargas contaminantes y mejorar la calidad del agua. Una de las medidas disponibles para los administradores de recursos hídricos es el establecimiento de Cargas Diarias Máximas Totales (TMDL), que normalmente limitan la concentración permisible de un contaminante en una masa de agua deteriorada. Si el objetivo en este caso es limitar la cantidad de P entregado a los cuerpos de agua aguas abajo, necesitamos determinar cuánto P constituye la concentración máxima permisible.
3.7 Reclutamiento de trucha
Dados los datos de cuatro pases consecutivos de electropesca en un alcance aislado de arroyo, ¿cuál es la población de truchas de arroyo de 0 años del arroyo?
Un método para estimar las poblaciones de peces en arroyos es aislar un alcance de arroyo con barreras aguas arriba y aguas abajo y realizar un tránsito de electropesca del alcance, recolectando y midiendo cada pez recuperado. Cuando se necesitan detalles adicionales o los peces son esquivos, es posible que se requieran múltiples pases a través del alcance, y los peces recuperados se retiran a un pozo vivo o al alcance adyacente. A través de este método de costo, el cambio en la captura entre pasadas consecutivas se puede utilizar para estimar la población real dentro del alcance. Para aislar la población de peces de edad 0 (jóvenes del año), se debe evaluar la edad de cada pez ya sea directa\(^{2}\) o indirectamente a partir de las distribuciones de longitud en la captura en cada pasada.
\(^{2}\)Se puede obtener una estimación de la edad no letal recolectando y observando escamas de peces bajo un microscopio
Los problemas anteriores se refieren a una variedad de cuestiones prácticas que podrían ser abordadas por un profesional de recursos naturales. Ninguno de ellos se expresa explícitamente como problemas matemáticos, pero los métodos cuantitativos podrían ser instrumentales para resolver cada uno de ellos. En efecto, esto es característico de muchos problemas reales de ciencia y gestión. Antes de que se conviertan en problemas cuantitativos, deben ser interpretados y cuidadosamente re-enmarcados (Figura 3.3). Esto no solo es una parte importante del proceso, sino que en muchos casos es el paso más desafiante y fundamental. En la práctica, esto debe ser parte del proceso de comprensión del problema y tal vez incluso de planear una estrategia de solución. En la mayoría de los casos, no se da suficiente información por adelantado y las expectativas para el tipo de solución deseada son vagas. En este sentido, son problemas mal estructurados, que requieren alguna digestión y una cuidadosa reformulación antes de que puedan entenderse como problemas cuantitativos solucionables.
Recopilar la información que se considere necesaria para llegar a la solución es, por supuesto, un paso esencial en el proceso. Cuando sea posible, debemos esforzarnos por incluir este paso como parte del trabajo del curso. Sin embargo, el diseño de experimentos y la logística para hacer nuevas mediciones de campo pueden y deben abordarse en sus propios cursos, y no podemos esperar hacer justicia a esas preocupaciones aquí. Como consecuencia, donde se abordan los problemas teaser aquí y en los capítulos siguientes, trabajaremos con datos hipotéticos o recabaremos datos reales de la literatura o de documentos gubernamentales y recursos web.
Es importante destacar que estos problemas también varían en el grado en que podríamos esperar saber que tenemos la respuesta “correcta”. Por ejemplo, efectivamente puede ser posible conocer exactamente la carga máxima de P entregada en el Problema 3.6 o el volumen de herbicida necesario en el Problema 3.2, siempre que tuviéramos información perfecta sobre la descarga de la corriente y el área basal del tallo, respectivamente. Sin embargo, para la mayoría de los demás problemas, la confianza de que tenemos una buena solución debe provenir de la confianza de que hemos hecho interpretaciones y suposiciones bien razonadas y utilizado manipulaciones y análisis técnicamente correctos. Así, parte de la carga de resolver tal problema es articular cómo se interpreta el problema y cómo se desprende de esa interpretación la estrategia de solución elegida. Cada uno de estos problemas proporciona pistas o señales implícitas sobre qué
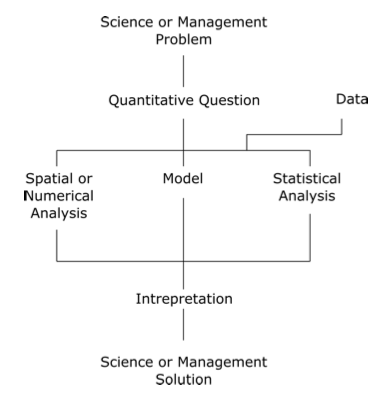
Figura 3.3: Una vía entre problemas y soluciones en el manejo práctico de los recursos naturales, incluyendo diversos enfoques cuantitativos.
tipos de estrategias son apropiadas para armar una solución. Por ejemplo, hay elementos espaciales claros para el Problema 3.1 y el Problema 3.2, pero también puede haber componentes espaciales más sutiles en otros. Por espacial, quiero decir que necesitamos incorporar información sobre qué tan grande o cuánto tiempo es algo en nuestra solución. Abordar estos elementos de problemas requiere de algunas herramientas desde la geometría y la trigonometría, así como quizás el lenguaje y convenciones de la geografía o la cartografía. Por lo tanto, este libro contiene varios capítulos que exploran los aspectos del razonamiento espacial que surgen frecuentemente en los recursos naturales.
El razonamiento espacial es el uso de información espacial o relaciones, como longitudes, áreas, volúmenes o direcciones, en la solución de problemas.
No es sorprendente que varios de estos problemas apunten a cuestiones de cuántos, particularmente el Problema 3.3 y el Problema 3.7. En estos y otros problemas, tal vez deseemos caracterizar individuos o poblaciones en términos de un valor representativo o distribución de valores, o tal vez necesitemos comparar valores o proporciones. Estas tareas involucran nuestra experiencia con la aritmética, estadística descriptiva y probabilidad, pero en muchos casos también requieren que seamos cuidadosos con las unidades y que podamos trabajar eficientemente con los números extremadamente grandes o pequeños que a veces se encuentran en las ciencias. Para estos temas, tenemos varios capítulos dedicados al razonamiento numérico.
El razonamiento numérico, como se usa en este libro, es la manipulación, caracterización, comparación e interpretación de valores numéricos (como los datos) al servicio de la resolución de problemas.
Aspectos de la mayoría de nuestros problemas se pueden expresar en términos de la relación entre múltiples variables, o relaciones entre causa y efecto. Por ejemplo, en Problema 3.5 podemos necesitar una forma de representar la relación entre cuánto esfuerzo se hace en las actividades de extinción de incendios y su costo. Como no necesariamente tenemos una idea anticipada de cuánto esfuerzo es apropiado, una expresión algebraica que relaciona la variable C (costo de los esfuerzos de supresión) con la cantidad de esfuerzo de supresión en sí (llamarlo S) podría interponerse y permitirnos emplear el razonamiento algebraico como un medio para una solución.
El razonamiento algebraico es el uso de variables generalizadas y relaciones formales entre ellas, más que números, como medio de restringir soluciones.
Finalmente, varios de estos problemas implican que buscamos una evaluación o predicción de cantidades o eventos futuros, hipotéticos o no observables. Por ejemplo, el Problema 3.4 parece preguntar si algo es posible incluso, aunque no sepamos qué es ese algo. En estos casos, encontrar una solución útil puede requerir modelado. Como se indica en el Capítulo 1, un modelo es la representación simplificada de sistemas reales y se construye con el propósito de explorar causa y efecto o relaciones funcionales entre variables a medida que se cambian las condiciones del sistema. Para modelar la propagación de la peste entre perros de pradera, entonces, es posible que necesitemos una forma de caracterizar la transferencia de pulgas entre un individuo infectado y un individuo no infectado, pero susceptible. Este tipo de razonamiento a menudo requerirá constructos algebraicos y suposiciones simplificadoras, y por lo tanto puede requerir competencia en el razonamiento algebraico. Aun así, sin embargo, se pueden obtener algunas ideas de la construcción del modelo incluso si las relaciones detalladas entre
El modelado en este libro se refiere a la construcción de una representación simplificada de sistemas reales o hipotéticos, a menudo descritos con una o más ecuaciones que relacionan variables entre sí y con propiedades del sistema, y utilizada para explorar fenómenos o relaciones complejos o inobservables.
las variables no se articulan formalmente con ecuaciones. Las Partes y Capítulos que siguen son elaboraciones y demostraciones de estrategias de resolución de problemas empleando cada uno de estos tipos de razonamientos. No todos serán aplicables a todos los problemas, y no hay necesariamente una secuencia de interdependencia. Por lo tanto, espero que más que leer el texto en orden, que lo consultes ya que surge la necesidad de ideas y perspicacia en los problemas que se te presentan. No proporciono soluciones completas a ninguno de los problemas teaser anteriores, pero sí uso partes de ellos para ilustrar conceptos y estrategias a medida que surgen.
¿Cuál de los problemas teaser descritos anteriormente te parece más interesante o convincente y por qué?
Usando como guía la tabla sobre la solución de problemas mal estructurados en el Capítulo 2, intente Comprender un problema teaser de su elección de la lista anterior. Escriba su respuesta a cada una de las preguntas bajo el mensaje Entender, o escriba “n/a” si no corresponde.
Intenta escribir uno o parte de uno de los problemas teaser como un problema matemático más convencional, con solo ecuaciones y sin palabras. ¿Qué tiene de desafiar hacer esto?
Escribe un problema propio en un formato similar a los problemas teaser anteriores: un título corto, una pregunta en negrita y un párrafo corto que elabore sobre el contexto o significado de la pregunta. Elige un tema de recursos naturales que te interese.


