4: Cantidades en el mundo real
( \newcommand{\kernel}{\mathrm{null}\,}\)
En este curso, buscamos resolver problemas prácticos en el manejo de recursos naturales y ecología, pero nos enfocamos en el uso de herramientas cuantitativas al servicio de este objetivo. Antes de sumergirnos demasiado en la resolución de problemas, debemos asegurarnos de saber qué se entiende por cantidades, herramientas cuantitativas y razonamiento cuantitativo. También estableceremos algunas convenciones sobre cómo se representan las cantidades en la ciencia y cómo se puede comunicar de manera más efectiva la información cuantitativa.
4.1 Cantidades en Recursos Naturales
Si podemos evaluar la presencia o ausencia de algo, contar su número, medir alguna propiedad que tiene, o compararla con otro objeto, se puede cuantificar. Esa cosa cuantificada se representa entonces por una cantidad que en sí misma ahora es propiedad de la cosa cuantificada. Si eso suena confuso, siga leyendo algunos de los ejemplos a continuación. Una cantidad completamente definida tiene cinco componentes:
- Nombre: como lo llamamos.
- Declaración procesal: cómo se mide o computa.
- Número: valor o valores numéricos correspondientes a magnitud o multitud.
- Unidades: cómo se escala.
- Símbolo: un carácter que representa la cantidad en ecuaciones.
Definir una cantidad puede parecer algo pedante, pero tiene implicaciones importantes para lo que podemos y no podemos hacer con ella. Esto contrasta fundamentalmente con las variables abstractas que encontramos en matemáticas de secundaria. En ese escenario, rara vez hay alguna razón para cuestionar si está bien y significativo agregar 3 x y 8 y, solo hacemos lo que nos piden. Pero en el mundo de las cantidades reales, si x significa “miligramos de cloruro de sodio” e y representa el número de huevos en un nido del Cardenal del Norte, no está tan claro que podamos realizar esa adición. Aunque lo hagamos, no está tan claro qué significa el resultado.
En el capítulo introductorio, reflexionamos sobre la encuesta de faisán en carretera de Iowa DNR y lo que significa para las poblaciones de faisán en todo el estado. El recuento de faisán produce un solo número cada año, por ejemplo 23.9 individuos por 30 millas en 2015. Descubrimos lo que significa esta cantidad y cómo se mide en la Introducción, por lo que ya tenemos la mayoría de los ingredientes de una cantidad completamente definida. Sólo necesitamos un símbolo. Este es un paso bastante trivial en problemas simples, donde la restricción principal es hacer que el símbolo sea inequívoco y sugerente de la cantidad que representa. Quizás entonces deberíamos elegir P para nuestro símbolo. Si tuviéramos que elaborar un documento que describa el levantamiento de faisán de carretera DNR, una vez que establezcamos cada una1 de las cinco propiedades de nuestra cantidad, podemos utilizar posteriormente P con la confianza de que la información transmitida por ese símbolo está claramente establecida: dentro del contexto de nuestro documento, P se referiría a la serie de estimaciones anuales de densidad de faisán según el método establecido por el DNR. Esta formalidad proporciona con ello un nombre taquigráfico y elimina cualquier ambigüedad en la discusión de cantidades. Tenga en cuenta que esto es diferente al P, el cual usamos anteriormente como símbolo químico para el elemento Fósforo. Si por casualidad estábamos trabajando en un problema que involucra tanto a faisanes como a Fósforo, podríamos seleccionar nuestro símbolo de manera diferente para evitar ambigüedades.
1Nombre, declaración procesal, número, unidades y símbolo
Como señalamos anteriormente, hay muchos tipos de cantidades que encontramos en la ciencia. Podemos tratar la información de presencia/ausencia como una cantidad, medida con una escala nominal2. ¿Había un garbanazo de cabeza negra en el comedero para pájaros a las 3:30 PM? ¿Hay algún escarabajo en la trampa que instalamos en un campo? Una cuantidad ordinal escalada es aquella en la que se clasifican u ordenan medidas individuales o componentes.
¿En qué orden llegaron y partieron diferentes aves del comedero3?
2Las cantidades nominales a escala toman la forma de categorías; algunos pares de categorías que se ajustan a esta definición pueden estar presentes o ausentes; infectados o no infectados
3Las cantidades a escala ordinaria tienen valores de acuerdo a su rango entre la población o datos.
En los casos anteriores, las distinciones entre las escalas son claras y obvias, pero en otros pueden ser más sutiles. Considera la expresión de la cantidad de temperatura. Tenemos varias escalas entre las que podemos elegir para medir y expresar la temperatura. Lo más importante y familiar son las escalas Fahrenheit, Celsius (Centígrados) y Kelvin (absoluta). La escala Celsius, por ejemplo, se define de acuerdo con los puntos de congelación y ebullición del agua, y las temperaturas a las que correspondieron esos fenómenos se definieron para tener valores de 0◦ C y 100◦ C, respectivamente. Por lo tanto, se define un grado de Celsius en una escala de intervalos4, donde una unidad de cambio de temperatura es 1/100 de la diferencia entre el punto de ebullición y el punto de congelación del agua. En contraste, Kelvin es una medida de la energía térmica absoluta contenida en una sustancia, en referencia a un estado teórico de energía cero5.
4Las cantidades escaladas a intervalos pueden tomar valores negativos.
5la escala Kelvin, llamada así por Lord Kelvin (William Thomson), se considera una escala de temperatura absoluta, midiendo la energía térmica absoluta en una sustancia.
Los kelvin son una escala de ratio, con un punto cero natural y una magnitud unitaria que representa el valor en una escala relativa a ese punto cero. Puede resultar confuso distinguir entre cantidades escaladas de intervalo y proporción, pero el siguiente ejemplo podría ayudar a iluminar la diferencia. Imagínese que midió la temperatura del agua superficial de un lago en un momento a mediados de marzo para ser de 1◦ C. Ahora suponga que regresó una semana después para encontrar que la temperatura ha aumentado a 2◦ C. Guau, la temperatura se duplicó, ya que 2 es dos veces más grande que 1! Bueno, no, no lo hizo Debido a que Celsius es una escala de intervalos, elegida arbitrariamente para tener un valor de cero a la temperatura de congelación del agua, no podemos decir que se duplicó. El problema con esto podría ser aún más claro si nuestra primera medición hubiera sido -0.1◦ C (¡superenfriada!) en lugar de 1◦ C. Entonces si aplicamos la misma lógica que antes para caracterizar el cambio a 2◦ C, tendríamos que decir que la temperatura es -20 veces el valor inicial, lo cual es ridículo. Es ridículo porque nuestra escala no tiene un punto cero natural, y en su lugar describe las diferencias de intervalo entre una temperatura medida y un punto de referencia estandarizado. En contraste, una temperatura de 300 K es en realidad dos veces más caliente que una temperatura de 150 K, ya que esta es una escala de relación7.
6Las cantidades con escala proporcional no pueden tener valores negativos; un valor no positivo indica una ausencia de la cantidad.
7Para una perspectiva tópica adicional sobre cantidades y escalamiento en ecología, consulte un recurso como Schneider, D.C., 2009, Quantitative Ecology, 2nd ed., Londres, Reino Unido, Academic Press, 415 p.
Puede parecer un poco esotérico definir cantidades y sus escalas unitarias con tanto detalle, pero ojalá ahora se pueda ver cómo diferentes escalas podrían conllevar reglas diferentes para qué manipulaciones son o no son significativas.
4.2 Qué es el razonamiento cuantitativo
El uso, la manipulación y la interpretación de la información cuantitativa son prerrogativas de científicos profesionales y gestores de recursos naturales. El término razonamiento cuantitativo se utiliza a menudo para describir los procesos de construcción y sentido de la información cuantitativa contextualizada8. Cuando buscamos patrones en los datos de calidad del agua, interpretamos tendencias poblacionales de faisán o estimamos el número de horas-persona requeridas para la remoción de arbustos invasivos en un bosque, estamos aplicando razonamiento cuantitativo. La aptitud de un individuo para el razonamiento cuantitativo a veces se denomina alfabetización cuantitativa.
8Un investigador describe el razonamiento cuantitativo como “razonamiento sofisticado con matemáticas elementales, en lugar de razonamiento elemental con matemáticas sofisticadas”. (Steen, L., 2004, Lograr la alfabetización cuantitativa: un desafío urgente para la educación superior, Washington, DC, MAA.)
Una premisa guía de este libro es que el valor de por vida de una alfabetización cuantitativa fuerte es mayor que el de las matemáticas puras para los profesionales de los recursos naturales. Sin duda, las habilidades matemáticas básicas son fundamentalmente esenciales para el razonamiento cuantitativo. Pero para la mayoría de los profesionales fuera de la ingeniería y las ciencias físicas, estas habilidades se aprenden principalmente en matemáticas de secundaria. Lo que a menudo no se aprende es cómo usar esas habilidades para dar sentido a las cosas en el mundo que nos rodea.
4.3 Unidades y dimensiones
Las cantidades con significado práctico para nosotros a menudo tendrán unidades. Considere algunos ejemplos aleatorios:
- Árbol de 71 pies de altura
- 16.4 gramos de suelo
- 42 gansos de nieve
- 39 respiraciones por minuto
- 385 ppm de dióxido de carbono
Cada uno de estos ejemplos perdería gran parte de su significado si solo dijéramos el número y no a qué correspondía el número: 71, 16.4, 42, 39, 385. Ciertamente podemos enchufar estos números en ecuaciones y trabajar con ellos en un sentido puramente matemático, pero probablemente ya no tengan un significado que nos importe. Por lo tanto, necesitamos hacer un seguimiento de las unidades. Las unidades pueden ser cualquier plantilla o escala estándar según la cual medimos una cantidad. Un pie, por ejemplo, aunque originalmente definido de manera holgada por la longitud del pie de un hombre griego o romano, ahora se define con referencia a un metro, que a su vez se define de acuerdo con la distancia que recorre la luz en un vacío durante un período de tiempo predefinido. Asimismo, los gramos y minutos son unidades de masa y tiempo definidos de acuerdo con referencias estandarizadas internacionalmente.
Prestar atención a las unidades y dimensiones no es mera formalidad. En las cantidades escaladas que utilizamos en la ciencia, las unidades y dimensiones constriñen qué operaciones matemáticas son permisibles.
Las dimensiones a veces se mezclan con unidades, pero el término es distinto y más amplio. En el uso casual, el término “dimensiones” de diez implica que deseamos saber qué tan grande es algo, es decir, su longitud, área o volumen. En las ciencias físicas, las dimensiones son una forma de agrupar diferentes tipos de unidades que pueden simplemente escalarse unas con otras. Pulgadas y centímetros son ambas longitudes. No importa qué objeto midas —tal vez la longitud total de una trucha joven de arroyo— si es de una pulgada de largo, es por simple conversión de unidades también de 2.54 centímetros de largo. Ambas son unidades de longitud. Pero sólo porque encuentro que el pez mide 1 pulgada o 2.54 centímetros de largo, eso no necesariamente me dice lo pesado que es. Entonces la masa es una dimensión fundamental diferente a la longitud, y ya sea que mida la masa en gramos o babosas, tiene dimensiones de masa. De hecho, la mayoría de las cantidades que tratan los científicos son compuestos de sólo tres dimensiones fundamentales: masa, longitud y tiempo. A veces usamos los símbolos [M], [L] y [T] entre corchetes para denotar cuando estamos hablando de dimensiones. También podemos tener cantidades adimensionales que podemos (por razones que veremos a continuación) denotar con [1], y que a menudo encontraremos cuando estamos tratando con escalas nominales, ordinales o multitudes.
La mayoría de las cantidades en las ciencias naturales tienen dimensiones que involucran masa [M], longitud [L] y tiempo [T]
Una cantidad compuesta por cualquier combinación de las dimensiones fundamentales puede denominarse cantidad derivada. La velocidad es un ejemplo de una cantidad derivada porque contiene implícitamente dos cantidades, una distancia o longitud recorrida durante un periodo de tiempo, [L T−1]. Tenga en cuenta que no hemos dicho si estamos midiendo la longitud en metros o pies o lo que sea, ni hemos dicho que el tiempo es en segundos, horas o milenios. Las dimensiones son más como categorías de unidades, y podemos convertir de un conjunto de unidades a otro dentro de cada categoría realizando multiplicación o división. La energía también es una cantidad derivada, y se puede expresar en unidades de Julios o Calorías. Pero independientemente de las unidades empleadas, cualquier cantidad de energía tiene dimensiones de [ML2 T−2]. Solo hay que tener cuidado si estamos trabajando con ecuaciones que no mezclamos unidades, o nos quedaremos con gobbledygook.
4.4 Comparación de manzanas y naranjas
Todos aprendemos en ciencias de secundaria o preparatoria a prestar atención a las unidades, y por una buena razón. Hacer un seguimiento de las unidades y asegurarnos de que nuestras unidades sean consistentes en cualquier cálculo que hagamos con las cantidades físicas puede evitar errores costosos. No estoy muy contento con ello, pero probablemente me paso unas horas al mes realizando minuciosamente conversiones de unidades en mi investigación —de hecho puede ser el tipo de cálculo más frecuente que hago, pero lo hago porque sé que es importante.
Consideremos un ejemplo simple artificial, similar al que encontraremos a finales de este semestre: supongamos que le dicen que el suelo en su patio trasero tiene 15.84 onzas de plomo por tonelada métrica de suelo. ¿Deberías preocuparte? Bueno, de acuerdo con las directrices de la EPA, se recomienda la remediación si las concentraciones de plomo en patios residenciales superan las 400 partes por millón. Partes por millón es una unidad adimensional similar a un porcentaje pero mucho más pequeña y puede corresponder a una masa (o volumen) de una sustancia contenida en una masa (o volumen) de alguna mezcla de sustancias. Nuestras medidas ya son ambas masas, por lo que 15.84 onzas/1 tonelada es [MM−1], y ya es adimensional, pero nuestras unidades no son consistentes. Podríamos arreglar esto de varias maneras diferentes, pero una simple podría ser convertir toneladas de tierra en onzas, para que tengamos onzas sobre onzas, produciendo unidades consistentes. Podríamos pasar mucho tiempo (no sabiamente, yo diría) configurando fracciones en papel para resolver esto (cuántas onzas en una libra, cuántas libras en un kilogramo, cuántos kilogramos en una tonelada.), pero mientras tengamos acceso a una computadora bien podríamos usarla. Muchas aplicaciones y sitios web harán conversiones de unidades básicas por usted, incluido el propio Google. Empleando uno de estos, vemos que hay 35274 onzas en una tonelada métrica, y ahora podemos expresar nuestra concentración medida como 15.84 onzas/35274 onzas, o aproximadamente 0.00045. Para convertir de este valor decimal a partes por millón, solo necesitamos multiplicar por un millón o 106 (al igual que se multiplicaría por 100 para obtener un porcentaje), dándonos aproximadamente 450 ppm de plomo. Entonces a 450 ppm, la concentración de plomo en nuestro suelo supera el umbral que la EPA ha considerado seguro, pero no es motivo de gran alarma.
4.5 Resolución de problemas sin números
Las dimensiones son tan útiles en la ciencia y la ingeniería que existen subdisciplinas enteras dedicadas al análisis dimensional. Si bien estas personas suelen utilizar el análisis dimensional como técnica para extraer relaciones entre variables en ecuaciones complejas que no se pueden resolver directamente, también podemos usar dimensiones para ayudar a resolver problemas más simples y detectar errores o inconsistencias. Esto se debe a que las ecuaciones físicamente significativas que describen las relaciones entre cuantitos deben ser dimensionalmente homogéneas9.
9La homogeneidad dimensional requiere ecuaciones, si se expresan solo en términos de las unidades que representan cada cantidad, para permanecer iguales
Es decir, las dimensiones de un lado de la ecuación deben ser las mismas que las del otro lado. Si conocemos las unidades de cada cantidad en una relación matemática y podemos calcular las dimensiones correspondientes, podemos comparar dimensiones a cada lado de la ecuación para verificar que es dimensionalmente homogénea. Esto puede parecer mucho como resolver una ecuación algebraica sin usar realmente ningún número, solo combinaciones de [M], [L] y [T]. ¡Hacer esto después de hacer algunas manipulaciones algebraicas en una ecuación es una forma práctica de verificar errores! De igual manera, si no estamos seguros de las dimensiones de una constante o variable en una ecuación, podemos resolver para esa constante en un lado de la ecuación y la agrupación dimensional en el otro lado, a través del requisito de homogeneidad dimensional, se aplicará a lo desconocido.
Al construir o manipular relaciones algebraicas, hacer cumplir y verificar la homogeneidad dimensional puede producir percepciones y detectar errores.
Las reglas para la manipulación algebraica de las dimensiones son sencillas. Se permite multiplicar, dividir o elevar a una potencia cualquier cantidad de cualquier dimensión, y la cantidad resultante tiene dimensiones que son el producto, cociente o potencia apropiado de las dimensiones originales. La suma y resta solo se puede hacer entre cantidades con dimensiones idénticas (y posteriormente se debe verificar que las unidades también sean idénticas). Consideremos un ejemplo donde deseamos encontrar las dimensiones de las entidades en una ecuación simple que describa la acumulación a lo largo del tiempo de insectos (medidos en masa) en una trampa de pozo:
m = m0 + kt (4.1)
donde sabemos que m es masa y así tiene dimensiones [M] y t es tiempo y así tiene dimensiones [T]. ¿Cuáles son las dimensiones de las otras dos variables? Bueno, asumiendo que la ecuación es dimensionalmente homogénea y sabiendo que el lado izquierdo tiene dimensiones [M], el lado derecho debe trabajar para tener dimensiones de [M] también. Además, dado que las cantidades agregadas deben tener dimensiones idénticas, sabemos que cada uno de los dos términos agregados en el lado derecho debe tener dimensiones de [M]. Entonces m0 es una masa, y k debe ser algo que, cuando se multiplica por un tiempo con dimensiones [T], da una masa. Por lo tanto, k debe tener dimensiones de [MT−1], o masa por tiempo.
Reorganizar ecuaciones algebraicamente con solo dimensiones o unidades en lugar de números es una manera útil de encontrar las unidades o dimensiones de variables desconocidas.
4.6 Comunicar información cuantitativa
Todos construimos nuestra comprensión de la información cuantitativa de manera un poco diferente. Yo personalmente capto patrones cuantitativos o relacionalidades mejor si lo veo en una gráfica. Otros podrían tener un tiempo más fácil leer o escuchar una descripción verbal de patrones y relación- barcos. Aún otros se verán más conmovidos por ecuaciones o listas de números. Podemos entender y comunicar información cuantitativa de todas estas maneras —y tal vez más (podemos codificar información cuantitativa en sonido, ¿verdad?)! Pero para ser científicos y gerentes bien redondeados, debemos ser capaces de crear e interpretar cada forma. El diagrama de la Figura 4.1 ilustra estas cuatro formas de comunicar información cuantitativa.
Esto es lo que significa cada uno de los nodos del triángulo:
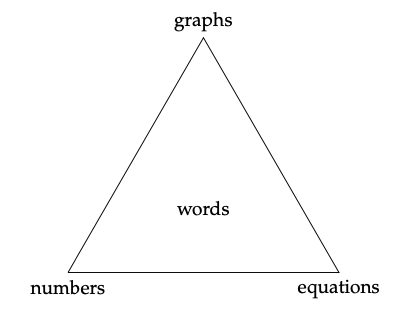
Figura 4.1: Formas de comunicar y entender la información cuantitativa.
• Gráficas, imágenes, figuras: cualquier exhibición visual de cantidades o relaciones entre ellas. Los gráficos estadísticos de una sola variable (por ejemplo, histogramas) y los gráficos bidimensionales (es decir, diagramas de dispersión x - y) serán los que más se encuentren, pero los mapas son otro ejemplo. A menudo la forma más eficiente de demostrar patrones o grandes volúmenes de datos.
- Números, en listas o tablas: para información numérica, la forma más directa, precisa e inequívoca de comunicar cantidades que no son demasiado numerosas (es decir, una lista corta).
- Ecuaciones, desigualdades o proporcionalidades: una forma formal y precisa de establecer relaciones hipotéticas, derivadas u observadas entre cantidades.
- Palabras, conceptos: descripciones e interpretaciones, ya sea de pie o para acompañar a otra forma de expresión.
En los informes técnicos, es una buena práctica emplear al menos dos o tres formas de expresión cuantitativa, donde una forma siempre serán palabras. Las palabras están en el centro del triángulo porque deben ser utilizadas para vincular conceptualmente las otras formas, y sin ellas no podemos afirmar ser comprensivos y comunicarnos de manera efectiva. Además, como profesionales, no podemos simplemente proporcionar gráficos o tablas de datos y esperar que hablen por sí mismos. Parte del papel de los científicos y gerentes es interpretar información cuantitativa y tomar decisiones o recomendaciones basadas en nuestras interpretaciones.
4.6.1 Ejemplo: reclutamiento de truchas de arroyo (teaser Problema 3.7)
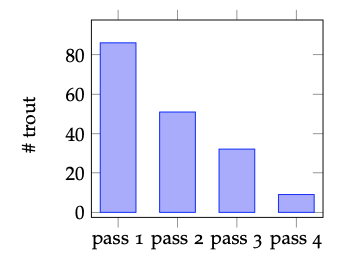
Figura 4.2: Gráfico de barras que muestra el número de truchas de arroyo extraídas de un alcance de arroyo durante cada uno de cuatro pases consecutivos de electropesca.
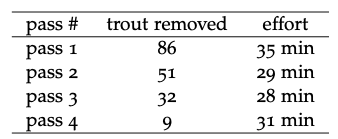
Cuadro 4.1: Remoción de trucha de arroyo de cuatro pasos de electropesca en un alcance de arroyos, incluyendo información sobre
el número de minutos (esfuerzo) transcurridos durante cada pasada.
Los datos de los estudios de electropesca de la población de peces y la estructura de edad pueden ser bastante simples. Una configuración típica comenzaría con el bloqueo del canal aguas arriba y aguas abajo con cercas o redes para evitar que los peces entren o salgan del alcance del estudio. Entonces los técnicos de pesca atravesarían lentamente el alcance del estudio con una persona aplicando los electrodos a través del agua y una segunda recogiendo los peces aturdidos en un cubo o vivirían bien. Los peces capturados se miden, pesan, envejecen (si se desea) y se devuelven al agua. En las encuestas de agotamiento, los peces son devueltos aguas arriba o aguas abajo de las redes de bloqueo, para evitar la re-captura inmediata. Los pases posteriores operarían de manera similar, y la presunción es que con cada remoción disminuye el número de peces que quedan en el alcance del estudio. La Figura 4.2 y la Tabla 4.1 muestran datos de cuatro pasadas consecutivas a través de un pequeño arroyo de trucha. El gráfico de barras (Figura 4.2) proporciona una indicación visual muy simple del cambio en el número de peces capturados en cada pasada. Gráficos como este pueden ser extremadamente valiosos para transmitir de manera eficiente tendencias o relaciones entre cantidades. Sin embargo, a menudo no permiten que los lectores o espectadores sepan con precisión cuáles son los valores de las cantidades mostradas. Además, las gráficas con demasiadas variables diferentes pueden llegar a ser demasiado complejas. Si queremos comunicar valores precisos de cantidades, particularmente donde hay múltiples tipos diferentes de variables, las tablas de datos como la Tabla 4.1 son quizás la mejor opción.
Dada sólo la información presentada ya sobre la captura electropesca de trucha de arroyo, la comunicación a través de ecuaciones es probablemente injustificada. Sin embargo, una narrativa textual es esencial para comunicar la naturaleza y el significado de los datos presentados en este ejemplo. Supongamos que no está familiarizado con los métodos de electropesca y agotamiento para la evaluación de la población de peces, ¿las barras de la Figura 4.2 y los números de la Tabla 4.1 contarían una historia clara? Los títulos de las figuras y los párrafos anteriores son esenciales para dibujar el significado de la figura y la tabla. Es por ello que las palabras están en el centro del triángulo en la Figura 4.1. Y es por eso también que la resolución cuantitativa de problemas es un esfuerzo intensivo en escritura. Si no podemos comunicarnos claramente sobre nuestras ideas, estrategias, resultados y conclusiones, la mayor parte del esfuerzo es para nada.
1. De nuestra lista con viñetas de ejemplos al inicio de la sección 4.3, ¿cuáles son las unidades y dimensiones para cada cantidad? Escríbelos con notación de corchetes cuadrados.
2. En estudios poblacionales, se reconoce que el número de individuos capturados depende fuertemente de cuánto tiempo (esfuerzo) se dedica a la persecución activa. Como resultado, una mejor variable para citar que el número de truchas capturadas es el número de truchas por unidad de esfuerzo, o captura por unidad de esfuerzo (CPUE). Si se define un minuto como la unidad de esfuerzo ba- sic para los datos del Cuadro 4.1, convertir los datos a una nueva variable, captura (trucha eliminada) por unidad de esfuerzo (minuto). Trace el resultado en una gráfica de barras similar a la Figura 4.2 y cree una tabla con esta variable adicional junto con las otras tres.
3. ¿Cuáles son las dimensiones de la nueva variable creada en #2?
4. ¿Qué tipo de cantidad se muestra en el eje horizontal de la Fig. 4.2? ¿Cómo cree que esto limita las formas adecuadas de visualizar estos datos gráficamente?


