8: Geometría y Geografía
- Page ID
- 107785
Uno de los tipos fundamentales de cantidades que utilizamos como científicos y profesionales de recursos naturales es una medida de distancia o tamaño. Ya sea que describamos los pies de tabla de la madera comercial en un pino ponderosa, la longitud de la horquilla de una trucha, el tamaño de la cordillera de un venado cola blanca o la capacidad de almacenamiento de un embalse de control de inundaciones, nos preocupan las cantidades espaciales que finalmente se manifiestan a partir de mediciones lineales en el espacio. Gran parte de esto puede resultarte familiar, pero hay mensajes importantes para llevar a casa al trabajar con cantidades espaciales simples y compuestas que te servirán bien para trabajar con mapas, fotos, planos de diseño y otras herramientas que utilizan los profesionales.
8.1 Longitud, área y volumen
Considera el humedal que se muestra en el siguiente mapa (Figura 8.1). ¿Cómo podríamos caracterizar su tamaño? Quizás la respuesta dependa del contexto de la pregunta. ¿Nos interesa hasta dónde está cruzarlo en una canoa? ¿Cuánto tiempo dura el hábitat de la costa para las aves acuáticas? ¿El número de acres que ocupa? ¿Y la cantidad de agua que contiene? A su vez estas preguntas apuntan a distancia lineal, distancia curvilínea, área y volumen, respectivamente. Cada uno de estos tipos de cantidades se puede expresar de diversas maneras\(^{1}\) según el entorno, la aplicación o el propósito de la comunicación.
\(^{1}\)Por ejemplo, podemos expresar todas las cantidades en términos de unidades SI de m, m\(^{2}\) y m\(^{3}\), o podemos usar unidades agrícolas más tradicionales de Estados Unidos como pies, acres y acre-pies.
Las distinciones entre longitud, área y volumen son más que simples trivialidades. Reflejan claramente no solo diferentes formas de estimar el tamaño, sino diferentes números de dimensiones espaciales. En el jerga común, la longitud es unidimensional o 1D, el área es bidimensional o 2D, y el volumen es tridimensional o 3D. Las unidades pueden ser una pista de cuántas dimensiones se indican en una descripción espacial. Del Capítulo 4, recordemos que podemos generalizar unidades en términos de las dimensiones fundamentales que conllevan. Desde esta perspectiva entonces, una longitud 1D tiene dimensiones de [L], un área 2D [L\(^{2}\),] y un volumen 3D [L\(^{3}\)].
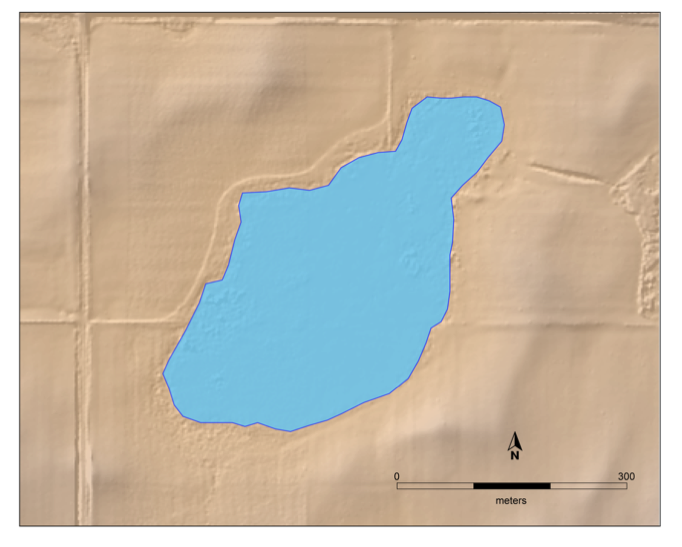
Figura 8.1: Mapa de un humedal en Iowa. El polígono azul muestra la extensión de las aguas abiertas estacionales superpuestas en relieve sombreado.
Esto es cierto independientemente de las unidades específicas utilizadas para describir la cantidad de interés, aunque a veces la dimensionalidad puede ser oscurecida por el uso de unidades compuestas. Por ejemplo, si nos dicen que un bosque es de 820,000 pies\(^{2}\), esa es una medida de área 2D directa. Si ese mismo bosque se describe como 126,000 pies de tabla\(^{2}\), ahora estamos hablando de un volumen de madera expresado en una unidad que no es particularmente transparente para los forasteros, aunque es habitual entre los silvicultores. Si necesitamos hacer cálculos que involucren cantidades de este tipo necesitamos estar seguros de que entendemos qué tiene sentido y qué no tiene sentido hacer; qué es permisible y qué no.
\(^{2}\)Un pie de tabla equivale a 144 pulgadas cúbicas de madera comercial; se puede visualizar como una tabla de 12 pulgadas de largo y 12 pulgadas de ancho que es de 1 pulgada de grosor.
Tenga en cuenta que algunas de nuestras unidades espaciales de uso común están compuestas por definición. Un acre, por ejemplo, es una unidad de área aunque no se exprese en forma de longitud cuadrada. Originalmente definida como el área de tierra que podría ser arada con bueyes en un día, un acre es de 43,560 pies\(^{2}\) o aproximadamente 4,047 m\(^{2}\). Si midieras un cuadrado de 208.7 pies en un lado, eso sería aproximadamente un acre. El primo del acre en unidades SI, la hectárea, es también una unidad de área con una definición más simple: una superficie de terreno de 100 m de ancho y 100 m de largo, o 10,000 m\(^{2}\). \(^{3}\)
Ni el acre ni la hectárea necesitan tener alguna forma particular, ni necesariamente necesitan ser contiguos, aunque suelen ser.
Ni el acre ni la hectárea necesitan tener una forma particular, ni necesariamente deben ser contiguos, aunque generalmente son.También estamos familiarizados con varias formas alternativas de expresar volumen con unidades derivadas, particularmente cuando se habla de líquidos. No es inaudito hablar de volúmenes de fluidos en metros cúbicos o pies cúbicos (particularmente si nos referimos al volumen por unidad de tiempo como lo hacemos al describir los flujos de los ríos en pies cúbicos por o), pero es más común escuchar volúmenes de fluidos expresados en galones, o litros. Todas estas son expresiones legítimas de volúmenes de fluidos (gas o líquidos) y algunas tienen relaciones relativamente sencillas con volúmenes en cubos de longitud: por ejemplo, 1 ml es lo mismo que 1 cm\(^{3}\) o cc. Sin embargo, si deseamos realizar cálculos más complejos que sumar o restar en tales cantidades, puede ser ventajoso convertirlos en unidades más fundamentales como metros cúbicos. Una interesante unidad de volumen mencionada anteriormente es el acre-pie, que (como se puede adivinar) es el volumen correspondiente a un área de un acre de algo que tiene un pie de profundidad. Esto significa que sus dimensiones son un área [L\(^{2}\)] veces una profundidad [L], por lo tanto es un volumen [L\(^{3}\)]. Nos encontramos con esta unidad de volumen a veces en descripciones de estanques o porque puede ser más fácil de visualizar, pero esto también puede dificultar la realización de cálculos.
8.1.1 Conversiones unitarias en el espacio
Aquí hay un ejercicio común que los estudiantes estadounidenses a menudo necesitan realizar en cursos de ciencias de la tierra, geografía o recursos naturales Mapa del\(^{4}\): measure a rectangular land area on a USGS con una escala en pies y millas, y convertirlo en metros cuadrados o kilómetros cuadrados.
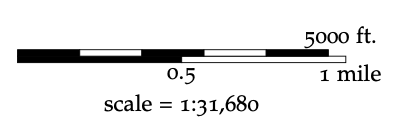
Figura 8.2:Una barra de escala de mapa genérica que muestra las distancias del mapa en pies y millas.
\(^{4}\)¡quizás este ejercicio va por el camino del mapa de papel en sí mismo ya que la gente interactúa cada vez más con solo mapas digitales en estos días!
Este ejercicio generalmente comenzará con cada estudiante a regañadientes haciendo marcas de marca en el borde de una hoja de papel que está alineada con la escala del mapa. A efectos de ilustración, seguiremos el camino hipotético (pero no infrecuente) de un estudiante que es propenso a cometer algunos errores comunes. Nuestro estudiante utiliza el papel marcado para estimar la longitud de cada lado de la superficie rectangular usando las unidades de mapa escalado\(^{5}\). Quizás los valores son 6.2 millas y 2.1 millas. Luego procede a multiplicarlos juntos, porque es consciente de que el área de un rectángulo es producto de sus lados. Por lo que golpea 6.2 × 2.1 en su calculadora y obtiene 13.02. Al pedirle abastecer unidades para su respuesta, razona que como las unidades en las que estaba midiendo distancias eran millas, la respuesta también está en millas. Su instructor señala que las millas son una unidad de longitud no área, y que debe escribir la ecuación completa con unidades para asegurar que su resultado salga en unidades de área. Entonces escribe:
6.2 mi × 2.1 km = 13,2 km\(^{2}\)
dejar las unidades fuera de cómputos puede generar errores en la asignación de unidades para soluciones.
y el instructor asiente con la aprobación pero dice, “y ahora necesitamos el área en kilómetros cuadrados”. Nuestro estudiante oprimido procede a buscar el factor de conversión entre millas y kilómetros: 1.609 km. Genial. Los botones de la calculadora hacen click de distancia hasta que el alumno, exasperado, indaga “entonces el área en km cuadrados es 13.02 × 1.609, lo que equivale a cerca de 20.95 ¿verdad?” El siempre paciente instructor sacude la cabeza: “hay 1.609 km en una milla, pero ¿cuántos km cuadrados en una milla cuadrada?”. Nuestro alumno mira fijamente el mapa y finge interés en la pregunta. Por capricho, pregunta “¿necesito cuadrar también los 1.609?” El instructor le da palmaditas en el hombro y comenta “sí, escríbalo todo, y no te olvides de las unidades” mientras ella se aleja. Nuestro alumno, aliviado de haber adivinado correctamente, escribe:
6.2 mi × 2.1 km = 13,02 m\(^{2}\)
\(13.02 \mathrm{mi}^{2} \times\left(1.609 \frac{\mathrm{km}}{\mathrm{mi}}\right)^{2}=33.71 \mathrm{~km}^{2}\)
Para ver por qué necesitamos cuadrar el factor de conversión como lo hizo nuestro estudiante en última instancia, escribamos la ecuación de conversión de la manera en que lo hizo al principio, pero usando solo las unidades (esta es una variación de la heurística de homogeneidad dimensional del Capítulo 4):
usando el factor de conversión de longitud para la conversión de área.
\ (\ {mi} ^ {2}\ veces\ {\ {km}} {\ {mi}} =\ {km} ^ {2}
Si cancelamos unidades comunes, deberíamos poder demostrar que las unidades del lado izquierdo son iguales a las unidades del lado derecho, pero aquí solo podemos cancelar millas en el numerador de millas en el denominador del lado izquierdo, dejando una ecuación unitaria sin sentido: mi km =\(^{2}\) km. Eso no puede ser cierto.
Si en cambio razonamos que nuestro factor de conversión necesita permitirnos cancelar a través para hacer las unidades equivalentes en ambos lados, cuadramos el factor de conversión y sus unidades para producir:
\(\mathrm{mi}^{2} \times\left(\frac{\mathrm{km}}{\mathrm{mi}}\right)^{2}=\mathrm{km}^{2}\)
Las conversiones de unidades se pueden escribir como ecuaciones con la cantidad actual y las unidades en el lado izquierdo y la cantidad en unidades deseadas en el lado derecho. Todos los factores de conversión deben incluir unidades y estar sujetos a operaciones tales que la expresión satisfaga la homogeneidad unitaria y dimensional.
Este enfoque también puede generalizarse para otros tipos de conversiones de unidades espaciales, siempre que nuestras unidades originales y deseadas no sean compuestas. Supongamos que estamos midiendo el tamaño de algo en unidades en función de la unidad de longitud U\(_{1}\) y necesitamos convertirlo en unidades en función de la unidad de longitud \(_{2}\)U.
Si el factor de conversión entre U\(_{1}\) y U\(_{2}\) es C\(_{1 → 2}\), la ecuación de conversión se puede escribir:
\(U_{1}^{d} \times C_{1 \rightarrow 2}^{d}=U_{2}^{d}\)(8.1)
En esta ecuación, d es la dimensionalidad espacial de la cantidad, por lo que es 1 para longitudes, 2 para áreas y 3 para volúmenes.
Es importante señalar que el factor de conversión C\(_{1 → 2}\) debe corresponder al número de unidades 2's por unidad 1, como hicimos para la conversión del área del mapa anterior.
Tenga en cuenta que los factores de conversión de unidades entre unidades compuestas como acres y hectáreas no están sujetos a estas preocupaciones. No existe tal cosa como un acre cuadrado porque un acre ya es una unidad de área, así que no hay que hacer nada al factor de conversión si estás convirtiendo de, por ejemplo, acres a hectáreas: hay 0.4047 hectáreas
en un acre, periodo. De esta manera estas unidades compuestas pueden hacer la vida más fácil, pero si estás trabajando simultáneamente con otras cantidades en metros, esta comodidad tiene un precio.
Se te podría haber ocurrido abordar el problema del mapa de una manera ligeramente diferente. Supongamos que en lugar de computar el área en millas cuadradas inmediatamente después de medir los lados del rectángulo, nuestro estudiante había convertido primero los lados de millas a kilómetros. ¿Esto hace alguna diferencia?
En este caso, las distancias del mapa son 6.2 × 1.609 = 9.976km y 2.1 × 1.609 = 3.379km. Su producto es de 33.71km\(^{2}\), que es el mismo resultado que antes. Eso no debería sorprender, ya que la única diferencia es que las conversiones unitarias de millas a km ocurrieron antes de encontrar la zona y no después. En efecto, esta es una forma de hacer que el problema sea un poco más sencillo de pensar, pero gracias a la propiedad conmutativa de la multiplicación no hay diferencia real entre los enfoques.
8.1.2 Escalas y Escalado
La barra de escala del mapa en la Figura 8.1.1 muestra no solo una escala gráfica que puede ser utilizada para medir directamente las distancias del mundo real desde la representación del mapa (escalado), sino que también indica una relación: 1:31 ,680. ¿Qué significa esta escala? ¿Tiene unidades?
Las escalas de mapa son como la mayoría de las demás proporciones adimensionales, como se discutió en el Capítulo 4 La belleza de muchas proporciones adimensionales es que podemos usar cualquier unidad que queramos en ellas siempre que ambas partes de la relación de escala o proporción tengan las mismas unidades. Entonces para la escala del mapa, podemos decir que 1 pulgada en el mapa es igual a 31,680 pulgadas en el mundo que representa el mapa\(^{6}\).
\(^{6}\)Para bien o para mal, EU aún persiste en usar pulgadas, pies y millas como medidas convencionales de distancia
en mapas y documentos oficiales. Aunque la mayoría de los científicos adoptaron el sistema métrico hace mucho tiempo, aquí retenemos unidades imperiales para reconocer la persistencia de unidades heredadas en nuestros mapas. Recordemos que el benchmarking es un proceso de conceptualización del tamaño de una cantidad comparándola con una cantidad de referencia conocida.
1 milla = 5280 pies
Si medimos un camino en el mapa que es de x pulgada de largo, la distancia que cubriríamos caminando por ese camino en el mundo real es de x × 31680 pulgadas. Esa no es una distancia muy fácil de imaginar porque no hay ningún punto de referencia muy familiar cerca de esa cantidad de pulgadas, pero podríamos convertir este último a pies o millas para hacerlo más simple, y luego podemos volver a expresar la escala en como una relación dimensional: 31680 pulg. × 1 pi./12 pulg. = 2640 ft.. Podemos ir un paso más allá aún: 2640 ft. × 1 mi./5280 ft. = 0.5 mi. Eso funciona bastante bien, ¡y a menudo lo hace por diseño! Así podemos reafirmar la escala del mapa como 1 pulgada = 0.5 millas, o equivalentemente 2 pulgadas por milla. Esto significa lo mismo que la relación de escala 1:31 ,680 pero es más específica porque ya hemos elegido las unidades con las que deseamos medir. Tenga en cuenta que no podemos decir que la escala del mapa sea 2:1 o 1:0 .5 porque al convertir el segundo número de pulgadas a millas hemos hecho que la declaración de escala sea específica de unidad.
Los mapas no son lo único que encontramos que son representaciones escaladas de la realidad. Cuando estamos aprendiendo sobre las propiedades microscópicas de moléculas o células, a menudo miramos diagramas o modelos físicos de cosas que son demasiado pequeñas para ver. Al mirar a través de un microscopio, percibimos una versión muy ampliada del objeto de estudio. En cada caso, estamos viendo representaciones de la realidad escaladas al tamaño que nos resulta más fácil de comprender. Es importante destacar que también estamos (generalmente) viendo las cosas escaladas isométricamente, lo que significa que todas las dimensiones se agrandan o encogen por el mismo factor constante. Veremos en capítulos posteriores algunos problemas interesantes asociados con el escalado que no es isométrico.
\(^{7}\)Este número proviene de: Junta de Investigación en Transporte y Consejo Nacional de Investigación, 2005. Evaluación y Manejo de Impactos Ecológicos de Caminos Pavimentados. Washington, DC: La prensa de las Academias Nacionales. https://doi.org/10.17226/11535.
8.1.3 Ejemplo: la zona de carreteras en un condado (Problema 3.3)
Un subproblema razonable a abordar en el tema de las colisiones de ciervos es ¿qué tan extendidas están las carreteras en la zona de interés? Al igual que con varios de los otros problemas teaser de este libro, no se cita ningún condado específico, así que como primera aproximación solo estimaré números para mi propio condado de origen: Story County, Iowa. Según Wikipedia, Story County tiene una superficie de 574 mi. La extensión de las carreteras en el condado de Story o en otro lugar de Estados Unidos es algo que podría evaluarse fácilmente con un sistema SIG, y que sin duda estaría entre las formas más precisas y eficientes de obtener este valor para condados específicos. No obstante, en aras de una primera aproximación intentemos algo más fácil. La literatura sobre los sistemas viales en Estados Unidos sugiere que hay alrededor de 1.2 millas de carretera por milla cuadrada de tierra, en promedio\(^{7}\). Claramente se trata de una subestimación en las zonas urbanas, y tal vez una sobreestimación en zonas rurales remotas. En el paisaje agrícola cuadriculado no tan remoto del centro de Iowa (Figura 8.3), una densidad de carreteras más cercana a 2 millas. /mi. \(^{2}\)es quizás más apropiado. Por esta estimación, mi condado tendría aproximadamente 2 × 574 = 1148 millas de carreteras. La densidad vial es informativa, pero solo nos lleva a la parte de la noción de área. Lo que necesitamos saber ahora, dado que tenemos longitud de carretera, es el ancho promedio de una carretera. Supongamos que esto es de 20 pies.
Para ser un área significativa, necesitamos decidir convertir la longitud en pies o la anchura en millas\(^{8}\).
\(^{8}\)Esta es una decisión aparentemente trivial pero aún significativa. En el marco de Schoenfeld para la resolución de problemas, tomar este tipo de decisiones deliberadamente con los objetivos más amplios y los problemas prácticos en mente es un ejemplo de control.
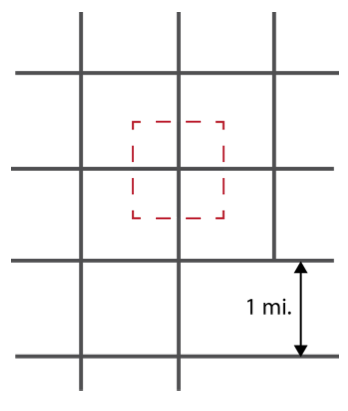
Figura 8.3: En el campo rural agrícola, las carreteras suelen estar dispuestas en una cuadrícula casi regular con una distancia de 1 milla. En estos escenarios, podemos estimar la “densidad de la carretera” imaginando una caja de millas cuadradas centrada en una intersección de carreteras. Dentro del cuadro que se muestra arriba, hay 2 millas de carretera, lo que sugiere una densidad vial de 2 millas por milla cuadrada.
Dado que el área del condado se estimó en millas, sería prudente para fines comparativos convertir el ancho de la carretera en millas también. Así, la carretera promedio es de aproximadamente 20/5280 = 0.003788 millas de ancho. Multiplicar ese ancho de carretera (en millas) por la longitud total de la carretera (en millas) arroja alrededor de 4.35 millas cuadradas. Eso es alrededor de 4.35/574 × ¡100% = 0.76% del área del condado!
8.2 Idealización o aproximación geométrica
Algunos problemas requieren mediciones espaciales o cálculos que son complejos, requieren mucho tiempo o difíciles de visualizar. En algunos de estos casos, una estimación aproximada puede ser adecuada para el tipo de soluciones que buscamos; en otros casos, es posible que deseemos establecer estimaciones rápidas antes de profundizar demasiado en los cálculos complejos, al igual que acabamos de hacer en la sección anterior. Para estos problemas espaciales, puede ser útil idealizar la información espacial que tenemos en términos de simples figuras geométricas de las que conocemos alguna cosa. Por ejemplo, supongamos que deseamos estimar aproximadamente cuánto podría pesar una serpiente de 40 cm de largo, y no tenemos información o experiencia previa en la que basar esta estimación. Si somos capaces de estimar su diámetro, podemos hacer algún progreso idealizando a la serpiente como un cilindro largo. Consultando la siguiente tabla, encontramos que el volumen de un cilindro se expresa como:
V =\(\pi\) r\(^{2}\) h (8.2)
donde r es la mitad del diámetro y h es la longitud de la serpiente. Si la r más grande es alrededor de 1cm y h es 40cm, una primera suposición para el volumen total es de aproximadamente 126\(^{3}\) cm. Ahora bien, si este radio corresponde a la parte más grande de la serpiente, este volumen podría ser un límite superior. Dado que el cuerpo de la serpiente se estrecha un poco, quizás sea mejor un radio medio —digamos 0.7cm. Ahora el volumen es de 61.6\(^{3}\) cm.
A continuación, dado que muchos animales no aviares tienen densidades cercanas a la del agua\(^{9}\), podemos estimar la masa de la serpiente usando densidad y volumen. Para ver cómo debemos hacer eso, podríamos usar una estrategia descrita en un capítulo anterior: escribir el problema con dimensiones justas. Estamos buscando cuánto pesa, pero realmente lo que queremos es una masa. Si enumeramos las dimensiones de las variables que tenemos y queremos, se ven así:
masa: [M] volumen: [L\(^{3}\)] densidad: [M L\(^{−3}\)] (8.3)
\(^{9}\)en las llamadas unidades cgs, la densidad del agua es de 1.0 g/cm\(^{3}\).
vemos que la masa que buscamos resolver aparece en el término densidad. El término volumen aparece como una tercera potencia negativa en el término de densidad y una tercera potencia positiva en el propio volumen, por lo que cuando se multiplican entre sí, volumen (V) y densidad (ρ) deben producir dimensiones de masa: m = ρ V. Si nos recordamos que la definición de densidad es efectivamente ρ = m/V, esto tiene sentido como una simple modificación algebraica de esa definición. Así, nuestra masa estimada para la serpiente sería:
61.6cm\(^{3}\) × 1.0g/cm\(^{3}\) = 61.6g. (8.4)
¿Esto es lo suficientemente cerca? Quizás, pero eso depende de la naturaleza del problema: ¿por qué deseamos saber cuánto pesa la serpiente y qué haremos con esa información?
8.2.1 Ejemplo: compra de herbicidas (Problema 3.2)
Podemos usar un enfoque similar para comenzar con el volumen de herbicida necesario para eliminar los arbustos leñosos del espacio verde de nuestra ciudad. Una suposición razonable es que, cuando se corta con una sierra o cortapelos, la sección transversal expuesta del tallo de una planta leñosa es aproximadamente circular. Si el objetivo es cubrir los tocones completamente con un recubrimiento de herbicida, cada tocón tendrá un volumen (de la Ecuación 8.2) igual a su área de sección transversal π r\(^{2}\) veces el espesor h del recubrimiento herbicida aplicado al muñón.
8.3 Medición del área del polígono
No todos los cuerpos espaciales de interés para nosotros se miden fácilmente utilizando las formas idealizadas simples revisadas anteriormente. Alternativamente, las idealizaciones geométricas introducen demasiado error para ciertas aplicaciones. Las formas no ideales pueden, sin embargo, ser aproximadas por polígonos irregulares en algunos entornos. Aquí, describimos un método para computar el área
de un polígono bidimensional de arbitraje usando un truco inteligente que frecuentemente se integra en CAD, GIS y otras edades de paquetes de software geoespaciales. El requisito principal que debemos cumplir para utilizar este método es tener pares de coordenadas para cada vértice del polígono en un sistema de coordenadas cartesianas (es decir, un plano con dos ejes lineales ortogonales; también conocido como plano x-y). Este algoritmo puede implementarse con bastante facilidad a mano, pero es mejor dejar en manos de una computadora encontrar el área de una forma más compleja. Echemos un vistazo a cómo funciona este algoritmo.
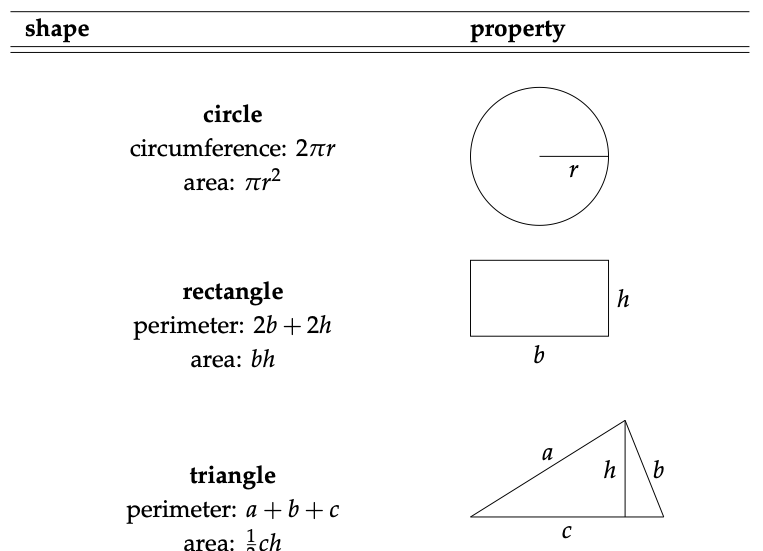
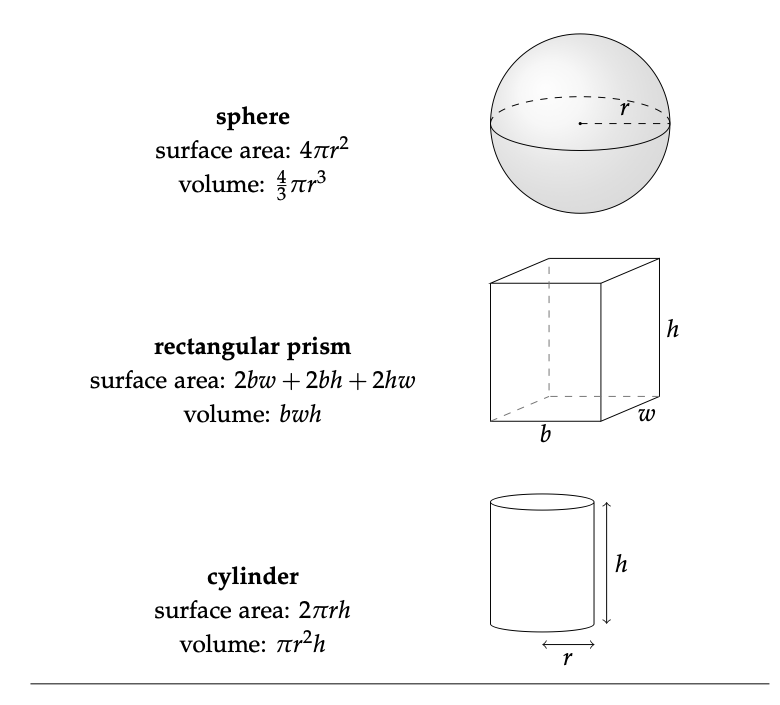
Tabla 8.1: Relaciones geométricas para formas comunes
En primer lugar, recordemos que un trapecio es una forma de cuatro lados en la que sólo dos lados son paralelos, como en la Figura 8.4. A primera vista, puede parecer que el área del trapecio sería un reto de estimar, pero cuando nos damos cuenta de que debe ser lo mismo que el área de un rectángulo que es tan alto como la “altura” promedio de dos tamaños verticales del trapecio, podemos ver algo de esperanza\(^{10}\). Sabemos que el área de un rectángulo es solo su altura por su ancho: A\(_{rect}\) = hw. Para un trapecio cuyos lados verticales tienen alturas h l y h r para la altura del lado izquierdo y la altura del lado derecho, respectivamente, podemos reafirmar la fórmula para área en términos del promedio de esas alturas:
\(A_{\text {trap }}=\frac{1}{2}\left(h_{l}+h_{r}\right) w\)(8.5)
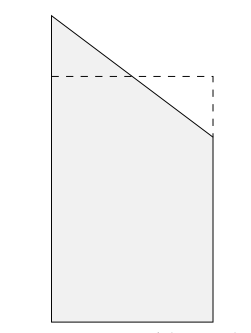
Figura 8.4: Un trapecio (en gris) con línea discontinua que indica el rectángulo con la misma área.
\(^{10}\)En la Figura 8.4 puedes imaginarte cortando el tope del trapecio en la línea discontinua, volteándolo y llenando el vacío en la parte superior derecha. Alternativamente, podríamos imaginar dividir el trapecio en un rectángulo más corto y un triángulo de ancho completo y calcular el área como la suma de esas dos áreas. Con un poco de álgebra, encontramos que el resultado es el mismo.
Ahora supongamos que en lugar de definir alturas y anchuras en términos de h y w, tenemos los vértices de nuestro trapecio en coordenadas cartesianas\(^{11}\). Cada punto en un vértice (esquina) del trapecio por lo tanto tiene una coordenada x, y, donde x se refiere a la dirección de la coordenada horizontal e y es vertical. En este sistema, tenga en cuenta que el ancho del trapecio se definirá por la diferencia en dos coordenadas x. Entonces, si tomamos la esquina superior izquierda en la Figura 8.4 para tener una coordenada x de x\(_{1}\) y la esquina superior derecha para estar en x\(_{2}\), el ancho del trapecio es x\(_{2}\) − x\(_{1}\). De igual manera, si nuestra altura trapezoidal se extiende a cero\(^{12}\) en la dirección de la coordenada y, la altura “promedio” de nuestro trapecio puede reescribirse sustituyendo y 1 e y 2 por h l y h r. Si hacemos estos cambios en la fórmula de área anterior, cualquier trapecio dado en nuestro sistema de coordenadas tiene un área:
\(A_{\text {trap }}=\frac{1}{2}\left(y_{1}+y_{2}\right)\left(x_{2}-x_{1}\right)\)(8.6)
\(^{11}\)Cartesiano solo significa que estamos especificando la ubicación de los puntos en un sistema de coordenadas bidimensional donde las direcciones de las coordenadas son perpendiculares entre sí. A continuación veremos que el sistema de coordenadas UTM para mapas es cartesiano, mientras que la latitud y la longitud no lo son.
\(^{12}\)de hecho podríamos demostrar que no necesita llegar hasta cero siempre que todos los valores y en la colección trapecial sean positivos todos son negativos, pero esto se deja como un ejercicio
Consideremos ahora el polígono representado en la Figura 8.5. Cada par de vértices adyacentes se puede ver como las esquinas superiores de un trapecio. Si aplicamos la fórmula anterior a cada par de vértices adyacentes y sumamos las áreas juntas, ¿qué obtenemos?
\ (\ begin {array} {r}
A=\ frac {1} {2}\ izquierda [\ izquierda (x_ {2} -x_ {1}\ derecha)\ izquierda (y_ {2} +y_ {1}\ derecha) +\ izquierda (x_ {3} -x_ {2}\ derecha)\ izquierda (y_ {3} +y_ {2}\ derecha) +\ lpuntos\ derecho. \\
\ izquierda. \ ldots+\ izquierda (x_ {1} -x_ {n}\ derecha)\ izquierda (y_ {1} +y_ {n}\ derecha)\ derecha]
\ end {array}\) (8.7)
Aquí, n es el número de vértices y los puntos suspensivos “.”. significa que hemos omitido algún número de términos en la ecuación, aunque en este caso solo tenemos cinco vértices así que solo hemos omitido dos términos. Observe que si etiquetamos sistemáticamente los vértices de nuestro polígono en sentido horario, aproximadamente la mitad de los trapezoides tendrán áreas negativas y la mitad tendrán áreas positivas, aunque las áreas negativas serán algo más pequeñas. Esto se debe a que a medida que nos acercamos por la parte inferior del polígono a medida que marcharemos en sentido horario desde un par de vértices hasta 7 el siguiente par, nuestras coordenadas x son cada vez más pequeñas a medida que avanzamos de derecha a izquierda. ¡Esto es bueno! El resultado es que el valor de ancho (y consecuentemente el área) calcula como negativo, y como resultado este trapecio inferior se resta del área total del polígono, ¡que es exactamente lo que queremos! Si ordenamos los vértices en sentido antihorario obtendríamos el resultado opuesto, pero el área resultante (negativa) seguiría siendo correcta.
Como se mencionó anteriormente, este algoritmo se implementa fácilmente en una computadora, ya sea usando software de hoja de cálculo como Excel, o software computacional/estadístico como R. Asimismo, este método está integrado en otras herramientas de software que utilizan estudiantes y profesionales de recursos naturales, incluyendo la mayoría de los paquetes SIG.
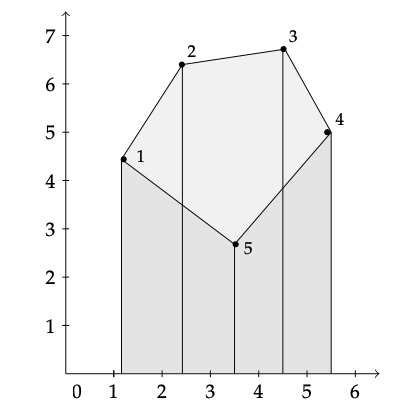
Figura 8.5: Un polígono arbitrario.
Usando el algoritmo trapezoidal, las áreas para trapecios individuales se calculan una por una en el orden de las agujas del reloj. En la parte inferior del polígono (donde el relleno trapezoidal es de color gris más oscuro), las áreas calculadas son negativas, recortando el área trapezoidal no deseada desde debajo del polígono.
8.3.1 Ejemplo: hábitat de aves acuáticas en aguas abiertas (Problema 3.1)
Una variable importante que influye en la abundancia de aves acuáticas es la presencia de diferentes tipos de hábitat. La mayoría de las aves acuáticas se alimentan extensamente en aguas abiertas, por lo que el área de humedal abierto es una variable de hábitat clave. En la Sección 8.3 identificamos el algoritmo trapezoidal como una herramienta para estimar el área de formas arbitrarias. También reconocimos que, si bien es posible hacer los cálculos requeridos a mano, automatizar el algoritmo mejora la eficiencia computacional por órdenes de magnitud. El algoritmo se puede implementar como una fórmula en una hoja de cálculo que contenga las coordenadas del polígono pero, como ya hemos comentado, esta operación es lo suficientemente común como para que se incorpore en la mayoría de los programas GIS. Por lo tanto, la comparación de áreas de cuencas hidrográficas entre las parcelas descritas en el Problema 3.1 es un problema geoespacial. Sin embargo, brindamos una oportunidad en el capítulo Ejercicios a continuación para trabajar con este algoritmo directamente.
¿Cuál es la distancia más larga a través del humedal en la figura 8.1?
Estime la relación de escala de mapa adimensional a partir de la barra de escala en la figura 8.1.
¿La escala del mapa sería la misma o diferente si hicieras una fotocopia ampliada de un mapa?
Utilice la aproximación geométrica para estimar el área del humedal en la figura 8.1.
Utilice el algoritmo trapezoidal para hacer una estimación más precisa del área del humedal. La tabla de datos a continuación contiene las coordenadas UTM del perímetro del humedal.




