9: Triángulos
( \newcommand{\kernel}{\mathrm{null}\,}\)
9.1 Medición con Triángulos
Es justo preguntarse por qué debemos molestarnos en aprender sobre los triángulos, ya que su relevancia para la ecología y los recursos naturales no es inmediata ap- parent. De hecho, los materiales naturales tienden a aproximarse a formas más tabulares o redondeadas, y los verdaderos triángulos son más difíciles de encontrar en la naturaleza en comparación. Pero el verdadero poder de los triángulos no está en donde los podamos ver, sino donde podamos imaginarlos. Lo creas o no, los triángulos imaginarios pueden ayudarnos a medir propiedades de un paisaje u organismo, y ese hecho está firmemente incorporado en muchas de las herramientas y tecnologías que utilizan investigadores y profesionales. En particular, las relaciones entre las longitudes de los lados del triángulo es una de sus claves como conjuntos. En este capítulo, revisaremos algunas de las propiedades de los triángulos y veremos cómo se pueden aprovechar estas propiedades para medir las cosas que nos importan.
9.2 Imprimación de trigonometría
La trigonometría es el estudio de los triángulos, específicamente las relaciones entre las longitudes de sus lados y los ángulos entre ellos. A primera vista, eso puede no parecer muy relevante para las ciencias naturales, pero algunos ejemplos podrían convencerte de lo contrario:
- Determinar la distancia “a medida que vuela el cuervo” entre dos puntos geográficos suele hacerse más fácilmente con la ayuda de triángulos.
- Medir la altura de un árbol o una montaña puede emplear triángulos.
- La telemetría a menudo utiliza la triangulación para determinar la ubicación geográfica de los animales de collar.
Si has tenido una clase de trigonometría, podrías asociar la disciplina con la manipulación de ecuaciones con sec 2 θ y cot (1 + π /2). Fuera de la clase de matemáticas, ¿alguna vez te encontraste necesitando encontrar la secante de un ángulo? No es probable. Pero no es muy raro encontrarse con los gustos de seno y coseno, que a menudo se escriben pecado y cos, respectivamente. Eso es porque son muy, muy útiles1. Y resulta que, ¡casi todas las otras funciones trigonométricas que quizás hayas aprendido se definen fácilmente usando senos y cosenos! Por ejemplo, la tangente de un ángulo puede definirse como la relación entre el seno del ángulo y su coseno, pero es tan útil que debemos reconocerlo también.
En lo que a mí respecta, en caso de que alguna vez necesites manipular una ecuación que contenga el coseno hiperbólico (cosh) de algo, puedes buscarlo o escribirlo en una herramienta de internet como Wolfram|Alpha. Si esta es tu primera experiencia con la trigonometría, no tengas miedo, ¡lo tomaremos con calma!
1En este punto tal vez solo necesites tomar mi palabra para ello, pero espero que aprecies este hecho para cuando termines este capítulo.
Wolfram|Alpha es una herramienta basada en la web desarrollada por el matemático y empresario Stephen Wolfram. Se basa en el mismo motor computacional subyacente que el software matemático Mathematica, pero se puede usar (de forma gratuita con una funcionalidad un poco limitada) desde cualquier navegador web. Además de realizar cómputos y simplificaciones algebraicas, puede intentar comprender preguntas escritas simples y puede recuperar datos de algunas bases de datos establecidas, concernientes por ejemplo al clima, el fincance y los deportes.
Similaridad
La similitud es un concepto que puede no presumir de suficiente sofisticación para garantizar su inclusión en una clase de trigonometría. Sin embargo, es una idea intuitivamente fácil de entender y su utilidad puede ser grande. Y afortunadamente para los científicos modernos, la aplicación formal de la similitud nos permite diseñar herramientas para medir las cosas de manera eficiente en el campo.
El principio de similitud geométrica2 es sencillo. Si tenemos una forma dada con longitudes de lado conocidas y/o ángulos conocidos formados entre los lados, podemos decir que otra forma es similar si tiene el mismo número de lados y una relación entre esos lados y ángulos que es la misma que nuestra forma de referencia. Las dos formas aún pueden ser similares aunque no sean del mismo tamaño u orientación. Si alguna combinación de traslación (mover la forma), rotación, reflexión (una imagen especular) o3 escala isométrica podría permitirle superponer una forma sobre la otra para encontrarla idéntica, las formas son similares.
En algunos campos este concepto está dotado de un nombre sonoro más sofisticado: la simili tude geométrica.
La palabra isométrica en este contexto significa que cualquier cambio en una dimensión espacial de una forma (por ejemplo, longitud) se corresponde con un cambio proporcional en todas las demás dimensiones.
Para los triángulos, los criterios de calificación para la similitud son simples, ya que solo hay tres lados y un ángulo interno en cada uno de los tres vértices. Para taquigrafía, cuando dos triángulos tienen un ángulo que es idéntico, lo llamaremos A. Cuando dos triángulos tengan los tres ángulos iguales, nos referiremos a que es AAA. Asimismo, si la longitud lateral de un lado de dos triángulos es igual, lo describiremos con S. Con estas definiciones, haremos las siguientes afirmaciones, aún no probadas, sobre los criterios para determinar la similitud:
Dos triángulos son similares si se puede establecer alguno de los siguientes:
• AAA. Los ángulos de un triángulo son iguales a los ángulos del segundo.
• SSS. Las longitudes laterales de un triángulo son iguales a las del segundo. Las longitudes laterales pueden ser escaladas por una constante C si esa constante es la misma para cada lado.
• SAS. Dos longitudes laterales y un ángulo de un triángulo son iguales a las del segundo. Las longitudes laterales pueden ser escaladas por una constante C si esa constante es la misma para cada lado.
Cuando hayas llegado al final de este capítulo, deberías poder mostrar cómo cada uno de estos criterios de similitud podría derivarse de uno de los otros. Eso se deja como un ejercicio para que trabajes, uno que pueda construir tu intuición para usar propiedades triangulares para la resolución de problemas.
9.2.1 El triángulo rectángulo y sohcahtoa
El mnemotécnico SOH-CAH-TOA es una de las pocas cosas que la mayoría de los estudiantes de trigonometría recuerdan años después de tomar la clase. De hecho, esta es una manera realmente útil de recordar los algoritmos que relacionan las funciones trigonométricas básicas con las relaciones entre los lados de un triángulo rectángulo4. Pero no revela nada sobre las formas en que los triángulos pueden emplearse con fines prácticos. Entonces, antes de tratar con estas funciones, volvamos a revisar qué es un triángulo rectángulo, dónde podríamos encontrarnos con uno, y algunos términos y reglas con respecto a estas bestias. La figura 9.2 muestra una bonita y de buen comportamiento.
Como ya sabrás, un triángulo rectángulo se define como un triángulo con un ángulo recto o 90◦
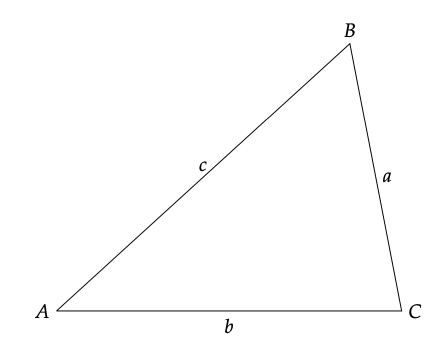
Observe que cada vértice (un punto de esquina) une dos de los tres lados y no toca el lado que está opuesto a él. Por razones que podrían ser evidentes en un momento, elegimos nombres para los lados y vértices que implican una relación entre un vértice y el lado opuesto a él. Entonces, por ejemplo, el lado a es el vértice opuesto A (es decir, el vértice A no es uno de los extremos del lado a). Probablemente satisfaga tu intuición de que el tamaño del ángulo en un vértice podría tener algunas relaciones simples con la longitud de su lado opuesto —al menos ahí hay una relación más intuitiva que entre el vértice A y uno de los otros dos lados. Imagínese mantener los vértices A y C estacionarios, pero permitiendo que el ángulo en A crezca. Es sencillo ver que si el ángulo A aumenta, el vértice B debe moverse hacia arriba y la longitud del lado a aumenta en consecuencia. Este experimento mental también produce resultados similares para los otros pares de lados y ángulos opuestos, y lo usaremos a nuestro favor en breve para tratar con la triangulación.
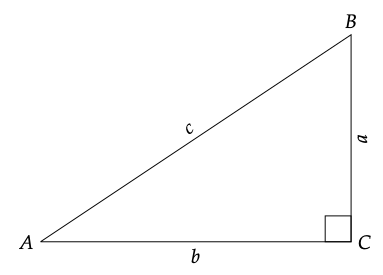
Figura 9.2: Un triángulo rectángulo.
Una de las propiedades más fundamentales de todos los triángulos es que los tres ángulos de vértice suman 180◦ (A + B + C = 180◦). Para el caso especial de un triángulo rectángulo, el ángulo recto por definición es 90◦, por lo que los otros dos ángulos deben ser menores a 90. Esto parece obvio, pero tiene una consecuencia importante: el lado más largo de un triángulo es el que está opuesto al ángulo más grande. Por lo tanto, dado que el ángulo recto es el ángulo más grande en un triángulo rectángulo, el lado más largo (al que llamamos hipotenusa) está al otro lado del ángulo recto (Figura 9.3).
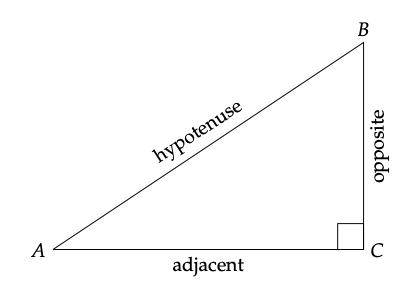
Figura 9.3: Un triángulo rectángulo.
Además de la regla de que los ángulos deben sumar 180◦, una de las propiedades más poderosas de los triángulos rectos es su adherencia al teorema de Pitágoras:
a2+b2=c2
Esto siempre es cierto siempre que c sea la hipotenusa de un triángulo rectángulo. Resulta que hay una simple modificación que se puede hacer a esto si estamos ante cualquier triángulo arbitrario. Pero antes de ir mucho más lejos, consideremos un ejemplo de configuración donde un triángulo rectángulo puede ser una ayuda útil para la medición.
9.2.2 Ejemplo: distancias terrestres
Si está visitando waypoints GPS almacenados como coordenadas UTM5, la distancia sobre el suelo entre dos puntos podría no ser obvia a partir de los conjuntos de coordenadas. Por ejemplo, ¿cuál es la distancia entre (452632,4660214) y (452991,4660580), las localizaciones marcadas de dos nidos de dickcissel observados? Una vez que reconocemos estos pares ordenados como el equivalente geográfico de (x, y) pares, es bastante fácil ver que el segundo nido es 452991 − 452632 = 359 m este y 4660580 − 4660214 = 366 m al norte del primero. Pero ni un dickcissel ni un ornitólogo probablemente irían de un nido a otro yendo primero 366 m al norte y luego 359 m al este. Ambos tendrían más probabilidades de ir aproximadamente en línea recta. Dado que este y norte son perpendiculares, podemos construir un triángulo como la Figura 9.4, con un lado absciente de 359 m de largo y un lado norte de 366 m de largo para representar las distancias de coordenadas. La distancia como el cuervo vuela es la hipotenusa del triángulo ya que es opuesta al ángulo recto. Por lo tanto podemos usar el teorema de pitágoras para encontrar esa distancia, que podemos llamar d:
\ begin {array} {l}
d^ {2} =(\ text {easting}) ^ {2} + (\ text {northing}) ^ {2} (9.2)\\
d=\ sqrt {(\ text {easting}) ^ {2} + (\ text {northing}) ^ {2}} (9.3)\ d=\ sqrt {(359 m) ^ {2}} (9.3)\
d=\ sqrt {(359 m) ^ {2}} + (366 m) ^ {2}} =513\ mathrm {~m} (9.4)
\ end {array}
Universal Transversal Mercator, o UTM, se refiere a un sistema de coordenadas geográficas proyectadas en el que las ubicaciones reciben coordenadas (metros este, metros norte) según su distancia en metros este y norte de un dato predefinido. El beneficio de las coordenadas UTM en comparación con la latitud y la longitud es que es un sistema de coordenadas ortogonales análogo al sistema de coordenadas cartesianas x - y que a veces usamos para la abstracción en matemáticas.
Saber que el segundo nido está a unos 513 m del primero es genial. Pero si tuvieras que darle instrucciones a un asistente de campo para que camine 513 m del primer nido para encontrar el segundo nido, eso por sí solo es información insuficiente para llegar al lugar correcto. ¿En qué dirección tiene que ir? Podrías, por supuesto, simplemente hacer que ella camine al norte 366 m y luego al este 359 m, pero eso no sería terriblemente eficiente. Lo que falta es obviamente la dirección. Si lleva una brújula, podrías darle una dirección de rumbo o brújula a seguir, pero ¿qué es ese rumbo y tenemos suficiente información para determinarlo?
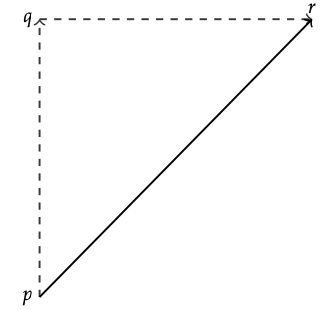
Figura 9.4: Distancias del nido de Dickcissel. El norte está hacia la parte superior de la página.
9.2.3 Ángulos y acimutos
En este punto, necesitamos trazar distinciones más importantes en cuanto a sistemas de coordenadas y convenciones. Cuando necesitamos ser más precisos que simplemente decir “noreste”, los rodamientos de la brújula son de diez dados como ángulos en grados. Algunas personas prefieren usar cojinetes de cuadrante, donde se dan indicaciones con respecto a desviaciones de norte o sur. Por ejemplo, debido noreste podría expresarse como “norte 45 este”, o equivalentemente N45◦ E. Eso puede interpretarse como 45◦ este del norte debido. Del mismo modo, el sureste podría ser S45◦ E y el suroeste es S45◦ W. Esto a veces puede ser más fácil de entender en la conversación, pero los rodamientos expresados en azimut son menos propensos a la mala interpretación. El acimut es la dirección de la brújula en grados en sentido horario desde el norte, aumentando continuamente de 0 a 360. En este sistema, el norte es tanto 0◦ como 360◦, este es 90◦, sur es 180◦ y oeste es 270◦ (Figura 9.5).
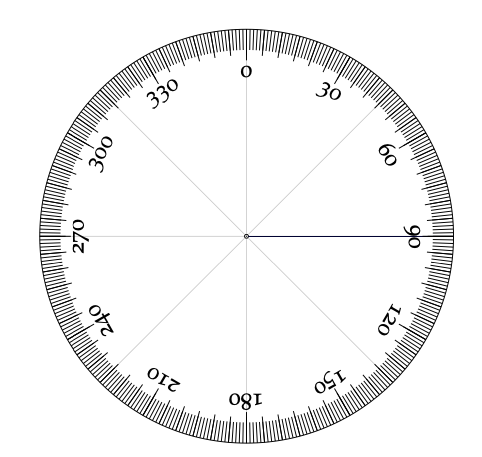
Figura 9.5: El sistema de coordenadas acimutales en una brújula. Gráfico modificado de D. Orescanin.
6En matemáticas y física, los ángulos también se miden frecuentemente en radianes en lugar de grados. Tenga en cuenta también que muchos programas de computadora que son capaces de hacer cálculos trigonométricos asumen que su argumento (o resultado deseado) estará en radianes. Los radianes tienen mucho sentido para la geometría porque, por definición, un radián es el ángulo atravesado cuando recorre una longitud a lo largo del perímetro del círculo que es igual al radio del círculo. Pero para su uso práctico en el campo, las titulaciones son más fáciles de trabajar. Así que aquí tienes una regla general rápida en caso de que necesites convertir: una vez alrededor de un círculo es 360◦ y 2 π radianes.
En el mundo de las matemáticas, los ángulos generalmente se miden en sentido antihorario desde el eje x. Esto no sólo significa que el punto de partida (0◦) está en un lugar diferente, sino que aumenta en una dirección diferente. Ocasionalmente emplearemos esta convención, ya que es tan prevalente en temas cuantitativos no relacionados con la geografía. Pero para el problema actual, nos quedaremos con el acimut.
Volviendo al problema de encontrar el nido dickcissel, ¿cómo podemos decidir qué rumbo darle al auxiliar de campo? Dado que las distancias de abscisa y norte son similares, podemos estar bastante seguros de que estará cerca de 45◦ (NE), pero probablemente no exactamente eso. Pero, ¿cómo se determinan los ángulos desconocidos en un triángulo cuando solo se conoce un ángulo (el ángulo recto) y todas las longitudes de los lados? ¡Ajá! seno y coseno al rescate!!
9.3 Ángulos, Círculos y Senos
Antes de continuar con la búsqueda del acimut, definamos más formalmente algunas cantidades trigonométricas. Lo haremos inicialmente en un marco matemático, usando un sistema de coordenadas x - y con ángulos que aumentan en sentido antihorario desde el eje x. La figura 9.6 muestra lo que podríamos llamar el “círculo unitario”, un círculo centrado en el punto (0,0) (también llamado el “origen”) con un radio de 1 unidad. Si elegimos algún punto del círculo, llámalo p, se encuentra a una distancia de 1 unidad del origen. Pero sus coordenadas no son obvias de inmediato. Al igual que en el caso de los nidos dickcissel, sin embargo, podemos romper el camino desde el origen a p en un componente en la dirección x y un componente en la dirección y. Conectando cada una de esas trayectorias componentes con la ruta directa (la línea de radio), terminamos con un triángulo rectángulo D OAH, como se ilustra en amarillo en la Figura 9.6.
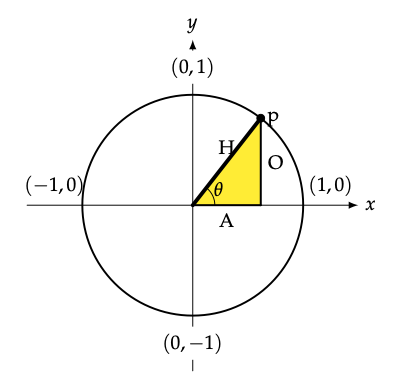
Figura 9.6: Triángulo recto inscrito dentro del círculo unitario.
Como tenemos un triángulo rectángulo, podríamos volver a usar el teorema de Pitágoras para encontrar una longitud de lado desconocida, siempre que conozcamos dos de los lados. Pero en este caso, no conocemos dos lados. En cambio conocemos el ángulo θ entre el eje x y la línea que conecta el origen con el punto p. También sabemos que esta línea, llamarla H para hipotenusa, tiene longitud 1 por definición. Los otros dos lados, O y A para opuesto y adyacente, son desconocidos pero se pueden encontrar a partir de las funciones trigonométricas fundamentales.
El seno de un ángulo es la relación entre la longitud del lado opuesto (O) y la longitud del lado hipotenusa (H).
El coseno de un ángulo es la relación entre la longitud del lado adyacente (A) y la longitud del lado hipotenusa (H).
La tangente de un ángulo es la relación entre la longitud del lado opuesto (O) y la longitud del lado adyacente (A).
La tangente es idéntica a la relación del seno al coseno de un ángulo, que se puede ver es equivalente a la definición anterior si se cancelan los términos de hipotenusa en la relación de proporciones. Estas son definiciones cargadas, así que tomemos unos momentos para reflexionar sobre lo que acabamos de ver.
- Las funciones trigonométricas son funciones en el sentido formal: convierten una entrada (ángulo) en una salida única (relación de longitudes laterales).
- Los lados opuestos y adyacentes se definen en relación con el ángulo que es el argumento de la función trigonométrica.
- La salida de cada función trigonométrica es una cantidad adimensional que representa la relación de dos longitudes laterales.
- Si conocemos un ángulo (que no sea el ángulo recto) y una longitud lateral, podemos encontrar las dos longitudes laterales restantes usando las funciones trigonométricas.
En las ecuaciones, no deletreamos el nombre completo de estas funciones, sino que usamos pecado, cos y bronceado como taquigrafía. Con esta taquigrafía y las definiciones anteriores, podemos construir algunas ecuaciones simples que pueden ayudarnos a encontrar las longitudes de lado desconocidas O y A en la Figura 9.6:
sin θ =OH (9.5)
cos θ =AH (9.6)
Como conocemos θ y H en el círculo unitario, podemos reorganizar estas ecuaciones para resolver las incógnitas. Multiplicando ambos lados de cada ecuación por H, obtenemos:
H sin θ = O (9.7)
H cos θ = A (9.8)
Ahora la razón por la que hemos hecho esto en el círculo unitario es que H = 1, así que esencialmente terminamos con las definiciones sin θ = O y cos θ = A. Una cosa importante a tener en cuenta, entonces, es que podemos escalar a cualquier longitud de lado arbitraria. Supongamos que nos interesaba no un triángulo con hipotenusa 1 unidad, sino uno con hipotenusa 55 metros. Definiendo f = 55 y escalando isométricamente todos los lados del triángulo por ese factor, podemos ver por ejemplo que:
sinθ=fOfH[mm](9.9)
Por supuesto, las f simplemente alargan H y O por el mismo factor común, y podrían cancelarse fácilmente. Pero esto ilustra el hecho de que el seno y otras funciones trigonométricas describen relaciones adimensionales de longitud lateral, ¡y que esas relaciones pueden escalar proporcionalmente sin cambiar el seno, el coseno y la tangente de los ángulos! Una implicación obvia es que si un vértice de un triángulo rectángulo tiene el mismo coseno y seno que otro triángulo, se puede mostrar que los triángulos son similares.
En realidad, ya lo sabíamos, ya que al conocer un ángulo distinto al ángulo recto en un triángulo rectángulo podemos encontrar fácilmente el tercero. Recordemos, entonces, que uno de los criterios para identificar similitud en triángulos es AAA, o igualdad de los tres ángulos independientemente de la longitud lateral. Para cualquier par de triángulos rectos similares, la única diferencia en las longitudes laterales es un factor de escala constante f.
Por lo tanto, cualquier triángulo rectángulo se puede reducir a uno similar en el círculo unitario dividiendo todas las longitudes de los lados por la longitud de la hipotenusa, de modo que H/f = 1!
Además de simplificar el escalado del triángulo, el círculo unitario también nos permite imaginar el punto p móvil a lo largo del perímetro y ob- sirviendo cómo cambian las longitudes de A y O en consecuencia. De hecho, el software Geogebra es perfectamente adecuado para hacer esto, y recomiendo encarecidamente jugar con él para impulsar tu intuición. Lo clave a notar es que el denominador de las relaciones laterales definidas como seno y coseno es la hipotenusa, o 1 en el círculo unitario. Entonces las longitudes de los lados opuestos (seno) y adyacentes (coseno) son la salida de esas funciones respectivas. Para ángulos entre 0◦ y 90◦, ambas funciones van de 0 a 1. Si permites que x e y tomen valores negativos a medida que el punto p va hacia abajo o hacia la izquierda del origen, verás que ambas funciones permanecen entre −1 y 1, inclusive.
Pero tangente es una historia diferente. Recordemos que una definición para la tangente de un ángulo es O/A. Se puede ver que para un ángulo pequeño θ, O es bastante pequeño y A está bastante cerca de 1, por lo que la relación de los dos será casi 0. O y A son iguales y tan θ = 1 cuando θ es 45◦, y a medida que
θ se acerca a 90◦, A se acerca a 0 y O se acerca al infinito, así tan θ se acerca al infinito como bien. ¿Qué supone que sucede a medida que θ se hace más grande que 90◦?
9.3.1 Ejemplo: clinometría de árboles
Una de las formas más comunes de medir la altura de un árbol es con un clinómetro. Se trata de un pequeño dispositivo de mano con una lente de observación y un punto de mira y uno de una variedad de mecanismos diferentes para medir el ángulo de inclinación (ya sea positivo o negativo) de la línea de visión desde la horizontal. La Figura 9.7 ilustra los triángulos hipotéticos construidos con vértices en el ojo del observador, y la base y copa del árbol objetivo. La obtención de la distribución de altura de la madera comercializable en nuestra parcela forestal en el Problema 3.5 podría incluir un conjunto de medidas representativas de altura con un clinómetro.
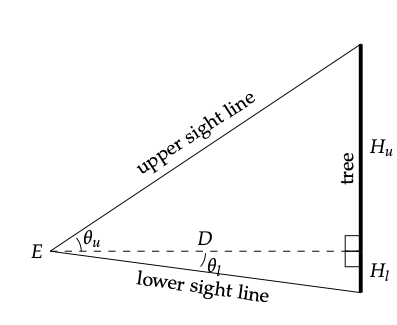
Figura 9.7: Medición de clinometría de la altura del árbol.
Al medir la altura de un árbol, a menudo se toman dos lecturas con el clinómetro: una a la copa θu y otra a la base o tocón θ l. El punto de observación E es una distancia predeterminada D del propio árbol. A partir de esta información, ¿cuál es la altura del árbol?
Identificamos H como la cantidad de interés, y observamos que H = Hu + Hl. Como primer paso, por lo tanto, debemos determinar H u y H l.
Suponemos que la geometría del problema nos permite construir dos triángulos rectos imaginarios como se ilustra y que nuestro clinómetro nos da ángulos en grados desde la horizontal. Ya que conocemos la distancia horizontal al árbol D y hemos medido los ángulos a la parte superior (θu) e inferior (θl) del árbol, conocemos la longitud lateral adyacente (D) y un ángulo para ambos triángulos. Las incógnitas objetivo son los lados opuestos de cada triángulo, y desde sohcahtoa sabemos que podemos usar tan para encontrar los lados opuestos cuando conocemos los lados adyacentes.
Así:
tan θu =HuD (9.10)
Dtan θu = Hu (9.11)
y
tan θl =HlD (9.12)
Dtan θu = Hl (9.13)
y desde H = Hu + Hl,
H = D tan θl + D tan θl (9.14)
H = D (tan θu + tan θl).
Así, podemos usar una función trigonométrica elemental (tan) y un poco de álgebra para producir una fórmula que relaciona las mediciones del ángulo del clinómetro con la altura del árbol.
9.4 Triángulos arbitrarios
Si bien algunos problemas pueden abordarse de manera rentable con triángulos rectos imaginarios, otros presentan triángulos sin ángulos rectos. Llamaremos a estos triángulos arbitrarios o generales. La triangulación es una tarea típica en la que los ecologistas o gestores de vida silvestre pueden encontrarse con triángulos arbitrarios. Cuando se rastrea por radio a un animal de collar, por ejemplo, un método para determinar la ubicación del animal en un momento dado es mediante triangulación desde múltiples antenas direccionales. La Figura 9.4 es la misma que la Figura 9.1, excepto que ahora estamos considerando que los vértices son radiotransmisores (animales) y receptores (ecologistas).
Hasta ahora, solo tenemos dos herramientas que son seguras de usar con triángulos que carecen de ángulo recto: la regla de que todos los ángulos interiores suman 180◦ (para lo cual podemos usar la taquigrafía (σ180) y los criterios generales para e implicaciones de triángulos similares. Estos pueden ser de uso limitado si nuestro objetivo es determinar la distancia o ubicación de un animal con collar. Pero si conocemos la longitud de un lado (digamos lado b en la Figura 9.4), y algunos ángulos, podemos hacer algunos avances.
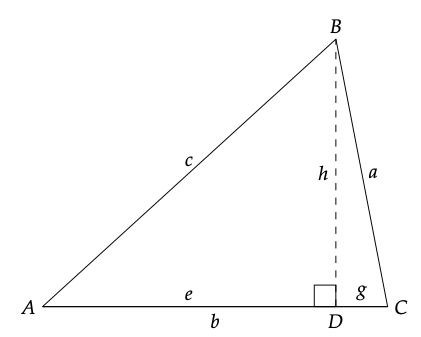
Figura 9.8: Triangulación en telemetría. B es un animal diana con collar radioeléctrico y A y C son antenas direccionales.
9.4.1 Ley de los senos
La ley de los senos es válida para los triángulos generales, incluidos los triángulos rectos. Si tenemos cuidado en definir nuestros lados y vértices como tenemos (con ángulo de vértice A lado opuesto a y así sucesivamente), podemos declarar la ley de los senos de la siguiente manera:
sinAa=sinBb =sinCc. (9.16)
Obsérvese que esta ecuación es extraña en que hay dos signos iguales. No se preocupe, esto es solo una taquigrafía que nos permite decir en una línea que cada relación entre el seno de un ángulo y la longitud de su lado opuesto es igual a las otras relaciones seno/lado correspondientes. Si escribiéramos cada ecuación con un solo '=', habría tres de ellas y simplemente tomaría más espacio. Pero en la implementación real se puede usar cualquiera de las igualdades implícitas en la Ecuación 9.16, tales como:
sinAa=sinCc (9.17)
El concepto clave aquí es que existe una relación simple y consistente- nave entre el seno de cada ángulo y la longitud de su lado opuesto, y que esto se aplica a todos los triángulos, sin importar el tamaño o la forma. Eso tiene mucho sentido, ¿verdad? Si te imaginas tomar un triángulo formado por tres gomas anudadas y alargando un lado (sin cambiar la longitud de los otros lados), ¿qué sucede con el ángulo opuesto a ese lado estirado? Crece ¿verdad? Pero para acomodar el crecimiento de ese ángulo, los otros dos ángulos deben hacerse más pequeños. La ley de los senos es especialmente útil si conoces dos lados y un ángulo (SSA) o dos ángulos y un lado (AAS).
9.4.2 Ley de cosenos
Otra herramienta que es útil para los triángulos generales se llama la “Ley de los cosenos”. De muchas maneras, proporciona la misma información que puedes encontrar fácilmente de otras herramientas que ya hemos comentado, por lo que no la derivaremos ni la discutiremos con gran detalle. Pero el matemático Paul Lockhart sostiene que la ley de los cosenos podría ser un nombre engañoso, y que la relación podría describirse mejor como una versión modificada del teorema de Pitágoras que es buena para todos los triángulos generales. Compruébalo:
c2 = a2 + b2 −2 ab cos C. (9.18)
Como se puede ver, es idéntico al teorema de Pitágoras salvo que existe un factor de corrección 2 ab cos C que se resta para dar cuenta de las desviaciones de un triángulo rectángulo. Al igual que con el teorema de Pitágoras, la ley de los cosenos te da la longitud del tercer lado si conoces a los otros dos, pero también necesitas conocer el ángulo entre los lados conocidos (SSA). Como tal, su función se superpone a la de la ley de los senos.
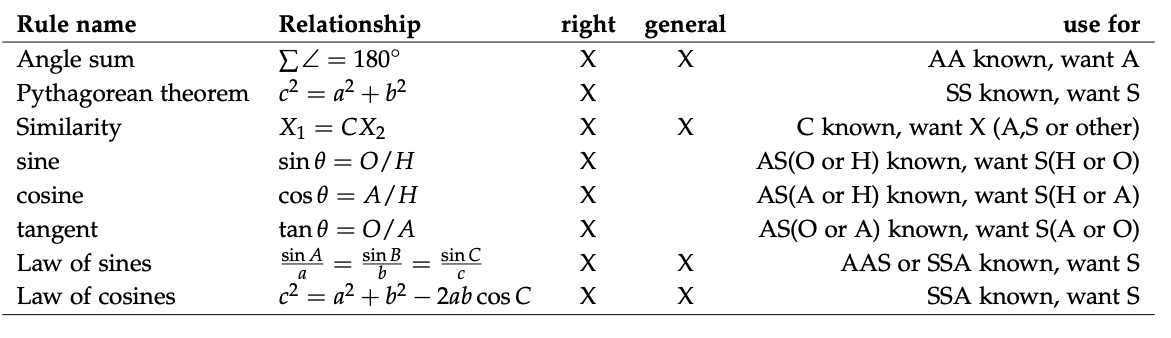
9.5 Herramientas triangulares: un resumen
La trigonometría es una gran subdisciplina de las matemáticas, y puede y lo hace llenar más de un semestre en clases de matemáticas. Nuestro tratamiento aquí se ha centrado en las herramientas que se encuentran más comúnmente en entornos prácticos de campo en las ciencias naturales. Muchas funciones adicionales, relaciones y habilidades pueden llegar a ser importantes en aplicaciones específicas y más técnicas, pero la mayoría de ellas pueden derivarse de las funciones básicas que aquí se discuten. Estas funciones y propiedades se resumen en la tabla que sigue.
9.5.1 Ejemplo: hábitat de aves acuáticas en la costa (Problema 3.1)
Algunas especies de patos incursionantes como los ánades reales parecen preferir aguas muy poco profundas. Esto significa que los humedales pequeños y poco profundos pueden ajustarse al pico, pero incluso las áreas poco profundas de la costa de humedales más grandes y profundos pueden ser adecuadas. Las costas también son la interfaz entre las áreas de alimentación y anidación para muchas especies, y a menudo soportan diversa flora y fauna a través del ecotono.
Una manera de estimar la extensión del hábitat costero es encontrar la longitud de los perímetros o contornos de los humedales. Si, como se describe en el último capítulo, hemos digitalizado (u obtenido datos existentes para) los contornos de humedales en nuestras parcelas candidatas, deberíamos tener coordenadas de absciente y norte para estos contornos. Al igual que con el área poligonal, la mayoría del software GIS computará automáticamente el perímetro de cualquier forma. Sin embargo, es instructivo ver cómo esto se desprende de nuestra discusión anterior sobre el razonamiento espacial asistido por triángulos.
Recordemos que cuando estábamos atravesando entre nidos de dickcissel, utilizamos una implementación del teorema de Pitágoras para encontrar la distancia en línea recta desde las coordenadas de ambos puntos finales. Podemos escribir esta relación en un sistema de coordenadas x, y de la siguiente manera:
l1→2=√[(x2−x1)2+(y2−y1)2](9.19)
donde l1→2 es la longitud de la distancia en línea recta desde el punto 1 (con las coordenadas x1, y1) y el punto 2. Observe que el resultado es siempre un número real, no negativo porque las diferencias son cuadradas. Si tenemos una serie de n puntos que describen los contornos del humedal, la suma de todas las n de las longitudes que forman un polígono cerrado se aproxima al perímetro P del polígono7. Podemos generalizar esto de la siguiente manera:
\ (\ begin {alineado}
P=\ sqrt {\ izquierda [\ izquierda (x_ {2} -x_ {1}\ derecha) ^ {2} +\ izquierda (y_ {2} -y_ {1}\ derecha) ^ {2}\ derecha]} &+\ sqrt {\ izquierda [\ izquierda (x_ {3} -x_ {2}\ derecha) ^ {2} +\ izquierda (y_ {3} -y_ {2}\ derecha) ^ {2}\ derecha]} +\ lpuntos\\
&\ lpuntos\ sqrt {\ izquierda [\ izquierda (x_ {1} -x_ {n}\ derecha) ^ {2} +\ izquierda (y_ {1} -y_ {n}\ derecha) ^ {2}\ derecha]}.
\ end {alineado}\) (9.20)
Al igual que con la fórmula de área trapezoidal, esta puede implementarse a mano, en una hoja de cálculo o con software GIS.
7¿Qué tan buena es este tipo de aproximación del perímetro? Esta es una pregunta simple con una respuesta no tan simple. Para nuestros propósitos aquí, cuantos más puntos tengamos, mejor, especialmente si tenemos una forma automatizada de hacer los cálculos. Sin embargo, en un sentido más filosófico este es el quid de la paradoja costera, primero popularizada por el matemático Benoit Mandelbrot.
1. Usa la Figura 9.4 y los triángulos rectos formados al soltar la perpendicular h, para derivar la ley de los senos a partir de las funciones trigonométricas que ya conoce.
2. Explica cómo podrías encontrar la ubicación telemetrada de B si conoces las ubicaciones de A y C y sus ángulos internos.
3. ¿Qué pasa si intentas aplicar la ley de los senos a un triángulo rectángulo?
4. ¿Qué pasa si usas la ley de los cosenos en un triángulo rectángulo? Supongamos que el ángulo C es el ángulo recto.
5. Los triángulos se pueden utilizar para medir objetos distantes, aunque no podamos llegar a ellos. Esto se puede utilizar para estimar la altura de un objeto (por ejemplo, un pico de montaña o un árbol) donde no podemos acceder a la base, y por lo tanto no podemos medir la distancia horizontal completa que nos separa del objeto que deseamos medir. La premisa general del método remoto se ilustra en la figura 9.9. Si podemos usar un clinómetro (un dispositivo para determinar el ángulo entre horizontal y una línea de visión a un objeto de interés) para determinar los ángulos de la línea de visión al objeto de interés p desde dos lugares diferentes b 1 y b 2, y conocemos la distancia entre esos lugares l, podemos usar trigonometría y álgebra para determinar la altura deseada H.
Diseñar una estrategia para medir H a partir de la información recopilada en b 1 y b 2. Derivar y justificar una fórmula que pueda ser utilizada para esta tarea.
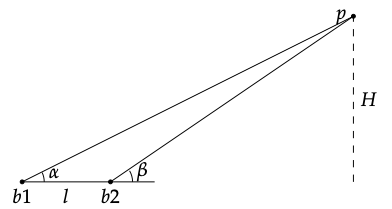
Figura 9.9: Abstracción triangular del problema de la montaña.


