10: Generalizar relaciones
- Page ID
- 107793
Hemos encontrado muchas instancias en este libro donde resolver un problema numéricamente requería números que no teníamos. A menudo no conocemos todos los números necesarios para resolver problemas reales. En algunos casos, la forma más sencilla de superar este problema es estimar o adivinar un valor. Sin embargo, en muchos otros casos, el valor de una cantidad importante no es constante en el espacio o en el tiempo; nuestra falta de conocimiento no es un reflejo de la incertidumbre en la medición. En cambio, hay una variación sistemática en el valor real de una cantidad y necesitamos permitir esos cambios. En estas circunstancias necesitamos tratar estas cantidades como variables que tienen valores numéricos desconocidos. Quizás tengamos alguna idea de cuán grandes o pequeños pueden llegar a ser los valores numéricos\(^{1}\), pero dentro de estos límites, la variable puede tomar cualquier valor.
\(^{1}\)Por ejemplo, si hemos utilizado estimaciones de estadio de béisbol y hemos elegido deliberadamente estimaciones de gama alta de algunos de los parámetros, esto podría proporcionarnos un límite superior aproximado sobre el valor de la variable de interés.
En este nuevo mundo de incertidumbre, tenemos a nuestra disposición las herramientas del álgebra. Al menos en partes del proceso de resolución de problemas, esto puede ser desorientador ya que tenemos que llevar símbolos en lugar de valores reducibles a través de cualquier operación que consideremos necesarias. Sin embargo, como veremos en breve, realizar manipulaciones simbólicas como medio para resolver problemas puede conducir a soluciones versátiles y reutilizables. Lo que hemos hecho antes de ahora puede llamarse especialización, donde buscamos valores numéricos particulares en cada cálculo cuando sea posible. La alternativa, que reconocerás como un escalón para el álgebra, es generalizar.
Expresar las cantidades variables necesarias para resolver un problema como variables simbólicas y manipularlas según las reglas del álgebra para producir relaciones generales.
Escribir relaciones algebraicas puede parecer hocus pocus al principio. Sin embargo, la mística se desvanece un poco cuando nos recordamos que las relaciones matemáticas son poco más que declaraciones lógicas formales. Al ensamblar cuidadosamente lo que sabemos sobre cantidades de interés, esforzándonos por mantener la generalidad y siguiendo algunos consejos, podemos comenzar a usar el razonamiento algebraico como una poderosa herramienta para la creatividad y la creación de sentidos.
- Identificar las variables y constantes relevantes
- Introducir notación descriptiva para cada cantidad
- Enumere lo que ya se sabe de cada variable, usando expresiones con notación simbólica cuando sea posible
- Busque formas de establecer expresiones iguales entre sí en función de lo que sabe; ¿hay dos formas de definir la misma cantidad usando las variables de interés?
- Adivina o inferir relaciones desconocidas
- Escribir y simplificar expresiones equiparadas como una ecuación simbólica
- Compruebe la consistencia dimensional o de la unidad
Cuando expresamos y manipulamos ecuaciones con variables simbólicas, estamos haciendo álgebra. Cuando declaramos relaciones sistemáticas entre variables simbólicas, estamos usando funciones. Las funciones pueden describir relaciones derivadas, hipotéticas u observadas, dependiendo de cómo lleguemos a ellas.
10.1 Familias de funciones
En las ciencias naturales y ambientales, se pueden utilizar algunas familias de funciones para describir las relaciones entre variables clave de interés. Exploraremos la más prevalente de este tipo de funciones, examinando su composición algebraica y las características de sus gráficas. En los capítulos siguientes, veremos cómo se pueden usar las funciones para describir las relaciones entre las variables medidas y cómo se pueden usar para idear modelos matemáticos.
10.1.1 Funciones lineales
La relación más simple entre dos variables —llamémoslas x e y — es quizás algo así como y = x. Esta relación es efectivamente una relación lineal, declarando solo que y es igual a x sin ninguna modificación, o que cualquier cambio en la variable x da como resultado un cambio idéntico en y. En realidad, rara vez nos encontraremos con alguna relación como esta que valga la pena describir en una ecuación. En cambio, a menudo podemos encontrar que las variables de interés están relacionadas a través de una constante de proporcionalidad, llamarla m (¡bien podría seguir con la notación que podemos haber visto en otra parte!). En este caso, y = mx sigue siendo una relación lineal, pero ahora para cualquier cambio en x, esperamos un cambio en y que sea m veces más grande que el cambio en x. Eso es lo que esta función hace por nosotros: convierte cualquier valor propuesto de x en una y correspondiente según la definición de la función. En efecto, la definición de una función en matemáticas es una operación que toma como entrada un valor de una variable explicativa o independiente y produce un valor para una respuesta única o una variable dependiente como salida.
He aquí un ejemplo: los colmillos de un elefante crecen continuamente con la edad, comenzando un poco menos de un año después del nacimiento. Aunque es probable que exista cierta variabilidad dentro de la población, esta relación permite a los biólogos estimar la edad del elefante. Así, una descripción matemática de esta relación puede escribirse como una ecuación lineal:
l = ra (10.1)
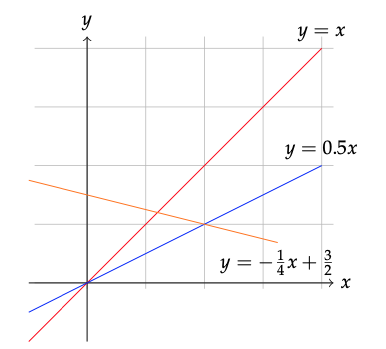
Figura 10.1: Diversas funciones lineales.
donde estamos llamando colmillo longitud l y edad a. Observe que esta forma de escribir la relación implica que estamos tratando a como una variable independiente (es decir, podemos pensarla como una especie de causa) y l es la variable dependiente (un efecto que depende de la causa). Dependiendo de las circunstancias, estos roles podrían cambiarse. De hecho, es más fácil medir la longitud del colmillo que la edad de un elefante dado, por lo que tal vez deseemos usar medidas de colmillos para ayudar a determinar la distribución de la edad en una población de elefantes salvajes.
También es importante recordar que cuando estamos haciendo ciencia en lugar de solo matemáticas, las variables suelen tener unidades y dimensiones, que discutimos anteriormente. Si esperamos que nuestra ecuación sea significativa, las dimensiones en los lados izquierdo y derecho de la ecuación deben ser consistentes (es decir, iguales).
Entonces en el colmillo de elefante ejemplo r = l/a es una tasa de crecimiento, debe tener dimensiones de longitud por tiempo, o [L T\(^{−1}\)] (vea como lo conseguimos? ¿sería lo mismo si cambiáramos nuestras variables independientes y dependientes?). Si hemos estado midiendo la longitud en pulgadas y la edad en años, nuestro valor para r debe estar en pulgadas por año.
¡Genial! Pero como dijimos anteriormente, podríamos desear en cambio conocer la edad en función de la longitud del colmillo. Así que tenemos que reorganizar un
poco las cosas. Ahora definamos m como el número de años de edad por pulgada de longitud de colmillo, que es solo el recíproco de r. En otras palabras, m = 1/ r, que también significa r = 1/ m. Como acabamos de tomar un recíproco aquí, las dimensiones de m son solo las recíprocas de las dimensiones de r, [T L\(^{−1}\)].
Ahora podemos replantear nuestra nueva relación lineal como l = a/m, o a = ml. De esta forma, tenemos la variable dependiente (edad) en el lado izquierdo de la ecuación y la variable independiente (longitud del colmillo) en el lado derecho, como es convención. Pero en este punto, ¿qué implica de la edad de un elefante si su longitud de colmillo es cero (l = 0)? Independientemente del valor de m, al enchufar cero a esta ecuación se obtiene a = 0. Por supuesto, como se mencionó anteriormente, los colmillos adultos no comienzan a desarrollarse hasta varios meses después del nacimiento. Entonces nuestra ecuación probablemente no sea muy buena para representar la realidad (particularmente para los elefantes jóvenes), y por lo tanto aún no es útil. Pero supongamos que íbamos a cambiar lo que queremos decir con “edad” en el lado izquierdo. Tiene sentido que lo que estamos midiendo sea el crecimiento a partir de la edad en que aparecieron por primera vez los colmillos, así que llamemos a esa edad a\(_{0}\), que es cercana a los 0.5 años. Entonces la edad del elefante que deseamos determinar es más de lo que hubiéramos predicho antes por la cantidad correspondiente a la edad en que aparecieron por primera vez los colmillos, a\(_{0}\). Entonces nuestra nueva ecuación, modificada para dar cuenta de esta corrección, dice:
a = a\(_{0}\) + ml (10.2)
En los términos abstractos pero precisos de las matemáticas, decimos que a es una función lineal de l con una pendiente de m y offset (o y-intercept) de un 0. Si bien parece obvio en el contexto de este ejemplo, el desplazamiento a 0 debe tener dimensiones de tiempo para que esta ecuación sea significativa. Tenga en cuenta que el valor de la tasa de crecimiento, o pendiente m, se puede determinar algebraicamente resolviendo la ecuación lineal anterior para m:
m =\(\frac{a - a_0}{l}\) (10.3)
que podríamos reconocer como el “ascenso” de la función, (a − a\(_{0}\)) dividido por el “run” l.
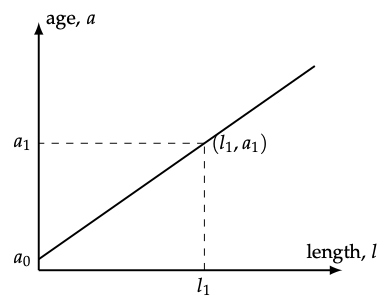
Figura 10.2: Gráfica de longitud de colmillo l en función de la edad a
En algunos casos es innecesario, pero en otros podemos necesitar especificar algo sobre el dominio (un conjunto de restricciones superior e inferior sobre los valores de la variable independiente) sobre el cual es válida una relación propuesta. Por ejemplo, no tiene sentido que un elefante tenga una edad negativa más que tener una longitud negativa de colmillo. Probablemente también haya un límite superior para la longitud del colmillo, aunque es difícil estar seguro de lo que podría ser. Para ser completo pero conservador, podemos especificar que el dominio de la función es 0 < l < 160 pulgadas. El rango para nuestra función lineal es el spread de valores mínimo a máximo de un correspondiente a los valores mínimo y máximo en el dominio. Tenga en cuenta que este último comentario se aplica a las funciones lineales (aunque a veces los signos se invierten), pero para algunas funciones no lineales de interés, los valores máximo y mínimo en el rango pueden no corresponder a los valores máximo y mínimo que delimitan el dominio. Veremos ejemplos de esto más adelante.
Las relaciones funcionales que son aproximadamente lineales son muy comunes en las ciencias. En efecto, un procedimiento rutinario en el análisis de datos multivariados es la regresión lineal, en donde se buscan los coeficientes (pendiente e intercepción) de una función lineal que mejor se ajuste a los datos. Las funciones lineales —o no lineales para el caso, como veremos a continuación— también se pueden postular hipotéticamente en la construcción de modelos matemáticos.
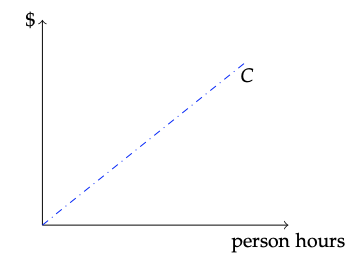
Figura 10.3: Ilustración esquemática de una hipotética relación lineal entre el costo de extinción de incendios y el número de horas de persona de esfuerzo de supresión.
10.1.2 Ejemplo: costos de extinción de incendios (Problema 3.5)
El tema de cuánto esfuerzo de supresión utilizar está en el centro de este problema, por lo que es claro que el esfuerzo de supresión debe considerarse una variable. Como es rutina con cantidades variables, debemos asignar un símbolo a la variable y decidir, al menos por ahora, con qué unidades se cuantificará. Un solo símbolo es preferible (aunque los subíndices son permisibles si es necesario) para evitar cualquier ambigüedad. Por lo tanto, escojamos el símbolo E para esfuerzo, y asignemos provisionalmente las unidades de horas-persona. Una persona hora tiene dimensiones de [1 T]. Al igual que acre-pies y otras unidades similares, las horas persona son unidades compuestas que debemos entender como el número de horas trabajadas por persona multiplicado por el número de personas. Por ejemplo, si dos personas trabajan 8 horas cada una, ese esfuerzo representa 16 horas persona.
Ahora tenemos que lidiar con la otra variable que está implícita en esta parte del problema: el costo. Primero, supongamos que definimos C como el símbolo que usaremos, y los dólares estadounidenses como la unidad de costo. Relacionar el costo de supresión con el esfuerzo requiere alguna forma de asignar un costo por unidad de esfuerzo. Recordando nuestra elección de unidades, este costo por unidad de esfuerzo tendrá unidades de dólares por persona hora, lo que seguro suena como un salario por hora. De hecho, ¡eso es exactamente lo que es! Entonces llamémoslo w. Ahora podemos afirmar el equivalente algebraico de la frase “costo de supresión equivale al número de persona horas de esfuerzo multiplicado por el salario por hora”. En símbolos:
C = Nosotros (10.4)
Esta ecuación se ilustra en la Figura 10.3 como una línea recta que aumenta de izquierda a derecha. La pendiente de la línea, análoga a m en nuestro concepto abstracto de la función lineal prototípica, es w, y la intercepción y es cero. Esta última observación simplemente articula la noción (ojalá obvia) de que el costo de cero horas de mano de obra debe ser de $0.
10.1.3 Funciones polinómicas
La función polinómica es aquella en la que la variable dependiente también depende de la variable independiente elevada a un exponente. Los polinomios se encuentran entre aquellas funciones que pueden tener múltiples altibajos en la variable dependiente sobre el dominio de la función. Para refrescar tu memoria, escribamos una ecuación polinómica abstracta para empezar:
y = b + mx + lx\(^{2}\) + kx\(^{3}\) + ... (10.5)
Aquí tenemos una función en la que las cantidades sumadas en el lado derecho tienen dependencia de potencias crecientes de x, y la forma en que la hemos escrito implicamos que la ecuación podría continuar in- definitivamente, incorporando poderes cada vez mayores de x a medida que avanzamos. Una forma de describir un polinomio es por su orden, que no es más que los valores enteros de los exponentes de x incluidos. Si quitamos el “.” de la ecuación anterior y simplemente detenemos la ecuación después de kx\(^{3}\), este sería un polinomio de tercer orden, ya que 3 es el exponente más alto de la variable independiente x. En ocasiones verás el término cúbico para polinomios de tercer orden, mientras que el término cuadrático se usa para polinomios de segundo orden.
Para estar completos, incluso podemos pretender que el primer término en el lado derecho b es realmente bx\(^{0}\), representando un término de “orden cero”.
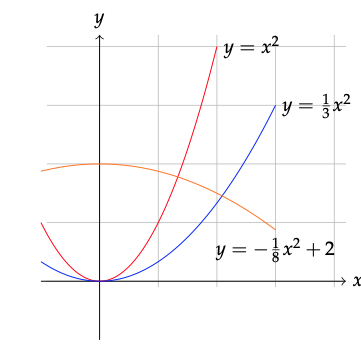
Figura 10.4: Funciones polinómicas.
Supongamos que nos deshicimos de los términos l y k en la ecuación anterior, lo que simplemente podríamos hacer diciendo que l = k = 0. Lo que queda es solo la función lineal que teníamos arriba, y vemos ahora que la función lineal es realmente un caso especial de una función polinómica, un “polinomio de primer orden”. Asimismo, si b = m = k = 0, nos quedamos con solo
y = lx\(^{2}\), un polinomio de segundo orden o cuadrático. Sigue siendo un polinomio de segundo orden si m y b son distintos de cero. Entonces ves que escribir la ecuación como lo hicimos anteriormente nos permite imaginar un polinomio de cualquier orden que escojamos, y mantener o descartar cualquier término que deseemos ajustando los coeficientes rotulados.
Entonces, ¿en qué se diferencian estas funciones polinómicas de las funciones lineales? Tomemos como ejemplo la fórmula para la superficie de una esfera — 2 quizás representando una gota de lluvia: A s = 4 π r. Una función lineal simple como se describió anteriormente tiene una única variable independiente y los valores de la variable dependiente dependen solo de la primera potencia de la variable independiente y una constante de proporcionalidad. Podemos escribir la ecuación del área de superficie como A = (4 π r) r, y ahora parece que solo tenemos la primera potencia de r. Genial, pero ahora nuestra constante de proporcionalidad contiene r, por lo que no es una constante en absoluto sino una variable en sí misma. Entonces las funciones no lineales son aquellas que no pueden escribirse como una relación entre la variable dependiente y la primera potencia de la variable independiente multiplicada por una constante constante de proporcionalidad.
Antes de perder demasiado tiempo hablando de polinomios, necesito ser claro en una cosa: Cuando nos encontramos con polinomios en la mayoría de las clases de matemáticas de pregrado, solo estamos considerando funciones donde los poderes de la variable independiente son enteros enteros. Con esto en mente, vale la pena pensar si son realmente útiles para nosotros. ¿Qué relaciones dependen de los poderes enteros de la variable independiente? Un área donde estos polinomios son útiles en ciencias naturales es la medición espacial. probablemente recuerdes que las áreas de cuadrados y círculos dependen cada una de la segunda potencia de una longitud característica (lado o radio). De igual manera, los volúmenes de esferas y cubos dependen del 3er poder (¿coincidencia?). Si bien es posible que nunca encontremos esferas y cubos perfectos en el mundo natural, podemos encontrar ocasión para idealizar el tamaño y la forma de algo (como un grano de arena, un huevo o una gota de lluvia como esfera, una raíz de árbol o una serpiente como cilindro, etc.) en un modelo sencillo para que podamos entender mejor algo al respecto.
De igual manera, algunos fenómenos físicos pueden describirse con ecuaciones que dependen de una potencia numérica entera (a menudo 2) de tiempo o posición. En problemas más complicados del mundo real, también puede resultar ventajoso aproximarse a una función rebelde utilizando una llamada expansión en serie de la función, que a menudo equivale a un polinomio.
A pesar de estos ejemplos, las verdaderas funciones polinómicas no surgen tan comúnmente en las ciencias naturales como lo hacen las funciones lineales y algunas otras no lineales\(^{2}\). Una excepción importante, con la que nos enfrentaremos bastante después de este término, es la llamada función de crecimiento logístico o dependiente de la densidad. En ecología, esta función describe el crecimiento teórico de poblaciones restringidas por espacios o recursos limitados. Podemos escribir la relación básica como:
G = rN −\(\frac{r}{K}\) N\(^{2}\), (10.6)
\(^{2}\)Pero como veremos a continuación, ciertamente existen relaciones en las ciencias natu- ales donde las relaciones entre variables se describen mejor con funciones que tienen exponentes no enteros.
donde la variable dependiente G es la tasa de crecimiento poblacional [1 T\(^{−1}\)], la variable independiente N es el número de individuos, r es una constante de crecimiento y K es la capacidad de carga. Esta función es cuadrática porque N\(^{2}\) es el término de mayor potencia.
10. 1. 4 funciones de alimentación
Además de las funciones lineales y polinómicas, es relativamente común encontrar al menos otras cuatro clases de funciones en las ciencias naturales. Las funciones de poder surgen comúnmente en ecología y geografía, especialmente en las propiedades de escalado de organismos y hábitats en el espacio. Las funciones de potencia pueden incluir cualquier función en la que la variable independiente se eleva a un exponente arbitrario, de la forma:
y = hacha\(^{ b}\) (10.7)
La función power difiere de un polinomio en que el exponente de la variable independiente no está restringido a ser un entero. La Figura 10.5 compara la apariencia de las funciones de potencia con exponentes mayores y menores que 1.
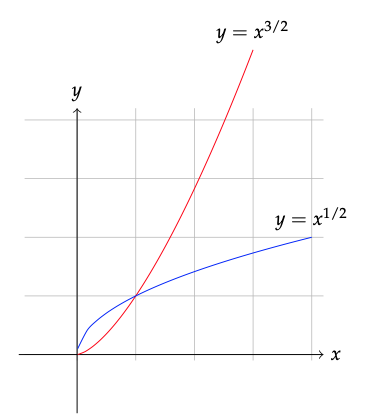
Figura\(\PageIndex{1}\): Copiar y Pegar Leyenda aquí. (Copyright; autor vía fuente)
En la subdisciplina biológica de la biogeografía insular, a menudo se ha descrito una relación entre el área de la isla A\(_{i}\) y la diversidad de especies S con una ley de poder:
\(S=c A_{i}^{z}\)(10.8)
donde c es un parámetro de ajuste y z es un exponente que suele ser menor que 1.
Otro ejemplo de una función de potencia aparece en la descripción de lo que los hidrólogos llaman la “geometría hidráulica” de un arroyo, que describe cómo la anchura, profundidad y velocidad promedio de un río cambian en el tiempo y el espacio\(^{3}\). El ancho de canal w, por ejemplo, típicamente aumenta aguas abajo de una manera que puede describirse como w = aQ\(^{b}\), donde Q, la descarga de agua, es nuestra variable independiente y a y b son constantes empíricas. La profundidad y velocidad del canal se describen con relaciones análogas.
\(^{3}\)Uno de los científicos que desarrolló y popularizó este concepto fue Luna Leopold (1915-2006), el segundo hijo de Aldo Leopold.

Figura 10.6: Ejemplos de funciones exponenciales simples.
10.1.5 Funciones exponenciales
Las funciones exponenciales son diferentes de las funciones de potencia en que la variable independiente aparece como parte del exponente, en lugar de la base. Una función exponencial genérica podría verse así:
y = a\(^{bx}\). (10.9)
La base a menudo puede ser e, que es un número importante (pero irracional como π) cercano a 2.718, pero no tiene por qué serlo. Las funciones exponenciales describen cambios cada vez mayores o decrecientes, y aparecen en contextos como la desintegración de sustancias radiactivas o el crecimiento desenfrenado de las poblaciones. La ecuación de desintegración radiactiva podría verse un poco así:
N = N\(_{0}\) e\(^{−λt}\) (10.10)
Una forma similar describe la extinción (atenuación) de la luz solar con profundidad en una columna de agua o dosel forestal según la ley Beer- Lambert:
I = I\(_{0}\) e\(^{−kd}\) (10.11)
donde d es la variable independiente. Además de los fenómenos naturales de crecimiento y decaimiento, las funciones exponenciales aparecen extensamente en el análisis económico.
A veces se utiliza una forma algo más complicada de función exponencial para describir el crecimiento de individuos (peces, árboles, etc.) a lo largo del tiempo. La función de crecimiento Von Bertalanffy (VBGF) se puede escribir:
\(L_{t}=L_{\infty}\left[1-e^{-K\left(t-t_{0}\right)}\right].\)(10.12)
En general, cuando el argumento exponencial es un número negativo, estas funciones describen decaimiento o enfoque asintótico hacia un valor limitante. Sin embargo, cuando el argumento es positivo, las funciones exponenciales describen el crecimiento explosivo.
10.1.6 Funciones logarítmicas
Estrechamente relacionadas con las funciones exponenciales están las funciones logarítmicas. El logaritmo natural, a veces escrito ln, es la función inversa de e, es decir, que ln (e\(^{x}\)) = x. El logaritmo de base 10, log escrito\(_{10}\) o simplemente log, se comporta de manera similar pero para funciones exponenciales con base 10. Entonces log\(_{10}\) (10\(^{x}\)) = x. Ambos tipos de registros, y logaritmos con cualquier otra base, son funciones que aumentan rápidamente para valores bajos de la variable independiente, pero que a partir de entonces aumentan cada vez más lentamente. Encontraremos logaritmos especialmente útiles en la transformación de datos que sospechamos que podrían ser una potencia o función exponencial, y por lo tanto deben tener un dominio básico de las reglas algebraicas que les aplican. Fuera de las transformaciones e inversiones exponenciales, sin embargo, no encontraremos logaritmos extensamente.
Dada la descripción de las relaciones especie-área dada en la Sección 10.1.4 y la noción de que el exponente z en la Ecuación 10.8 es menor que 1, describir lo que esto significa conceptualmente. ¿Cómo cambia la diversidad de especies con el área de la isla y cómo un incremento del cambio de área afecta a las islas pequeñas de manera diferente que a las islas más grandes?
Usando solo variables y constantes simbólicas, escribir una expresión que defina ese tiempo necesario para que el 95% de un isótopo radiactivo se desintegre. Pista: interpretar esto para significar que buscamos una expresión para t cuando N/N\(_{0}\) = 0.05.
Revisa la descripción de Problema 3.2. Escribir una ecuación algebraica hipotética, pero bien justificada, relacionando el volumen de herbicida necesario para eliminar los arbustos leñosos, y el área basal por unidad de superficie de esos arbustos. Considera que todas las cantidades son variables, así que usa símbolos en lugar de números para esto.
Revisa la descripción de Problema 3.1. Usando idealizaciones geométricas razonables (no algoritmos informáticos), ¿se puede escribir una ecuación algebraica simple que relacione la longitud del hábitat perimetral de un humedal con el área del humedal?


