11: Relaciones entre variables

En el capítulo anterior, nuestra discusión de variables y funciones asumió en gran medida que las relaciones se conocían o desarrollaban independientemente de cualquier medida o dato. Sin embargo, las relaciones funcionales entre variables también se pueden derivar de los datos. Aquí, exploramos dos conceptos que nos ayudan a comprender la fuerza y naturaleza de las relaciones sistemáticas entre variables.

11.1 Correlación

En el lenguaje común, la palabra correlación sugiere que dos eventos u observaciones están vinculados entre sí. En el análisis de datos, la definición es casi la misma, pero incluso podemos ser más específicos sobre la manera en que se vinculan los eventos u observaciones. La medida más directa de correlación es el coeficiente de correlación lineal, que generalmente se escribe r (y está, de hecho, relacionado con la r\(^{2}\) que citamos al evaluar el ajuste de una ecuación de regresión). El valor de r puede variar de -1 a 1, y cuanto más cerca esté de los extremos de este rango (es decir, | r |→ 1), más fuerte es la correlación. Podemos decir que dos variables están correlacionadas positivamente si r está cerca de +1, y negativamente correlacionadas si r está cerca de -1. Las variables mal correlacionadas o no correlacionadas tendrán r más cerca de 0.

En el margen hay dos parcelas que comparan la historia de vida y los rasgos reproductivos de diversos mamíferos. En la primera, Figura 11.1, la disposición de los puntos en una banda de abajo izquierda a superior derecha en la gráfica es relativamente fuerte, correspondiente a una r relativamente alta de 0.73. En contraste, la correlación entre el número de camadas por año y el tamaño de la camada en la Figura 11.2 es (¿sorprendentemente?) débil, produciendo más de un patrón de escopeta y r a modesto 0.36.

En resumen, se puede escribir la fórmula matemática para la correlación entre dos variables, x e y:

\(r=\frac{1}{n} \sum_{i=1}^{n}\left(\frac{x_{i}-\bar{x}}{\sigma_{x}}\right)\left(\frac{y_{i}-\bar{y}}{\sigma_{y}}\right)\)(11.1)

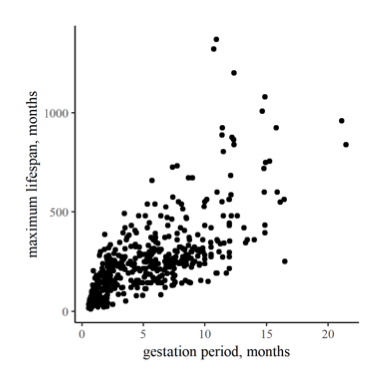
Figura 11.1: Correlación entre la vida máxima y el periodo de gestación de diversos mamíferos, r = 0.73.

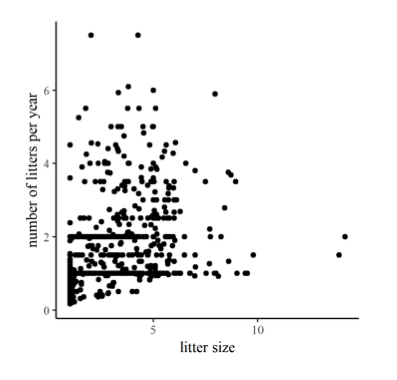
Figura 11.2: Correlación entre el número de camadas por año y el tamaño de camada de diversos mamíferos, r = 0.36.

donde el subíndice i corresponde a la i-ésima observación, la barra superior indica valores medios, y σ x y σ y son desviaciones estándar. Los detalles de esta fórmula no son de gran interés para nosotros. Lo importante a entender es que cuando los cambios positivos en una variable están claramente vinculados con cambios positivos en una segunda variable, esto indica una correlación buena, positiva, r > 0. Lo mismo es cierto si los cambios negativos en una variable corresponden a cambios negativos en la otra. Sin embargo, los cambios positivos en una variable correspondientes a cambios negativos en otra indican correlación negativa, r < 0.

También es importante señalar que esta es una buena medida de correlación solo para las relaciones lineales, e incluso si dos variables son estrechamente interdependientes, si su dependencia funcional no es lineal, el valor r no será particularmente útil. Sin embargo, la correlación aún puede ayudarnos a identificar las relaciones clave cuando encontramos por primera vez un conjunto de datos. Considerar los cambios en las variables meteorológicas medidas en una estación meteorológica en función del tiempo. Los datos meteorológicos pueden ser muy abrumadores debido a la cantidad de variables y al gran volumen de datos. Una manera práctica de aislar algunas de las interdependencias más fuertes entre las variables de interés es buscar correlaciones. Una gráfica de matriz de correlación es esencialmente una cuadrícula de parcelas donde cada variable se grafica contra todas las demás variables en una matriz cuadrada de paneles. Las relaciones con fuertes correlaciones positivas o negativas saltan inmediatamente, sugiriendo qué relaciones podríamos desear investigar más a fondo. Por ejemplo, veamos un conjunto de datos meteorológicos de un mes descargado de www.wunderground.com.

Hay mucha información en estas parcelas, así que vamos a verlas pieza por pieza. Observe que los paneles en la diagonal de arriba izquierda a inferior derecha serían una variable trazada contra sí misma (r = 1), y por lo tanto son reemplazados por una distribución de densidad para cada variable. También fíjese que dado que la mitad superior derecha sería una imagen especular de la parte inferior izquierda, solo hay un número en cada uno de esos paneles en lugar de una parcela. En cualquier caso, aquí acabamos de seleccionar cuatro variables de interés potencial, e inmediatamente se puede ver que existe una fuerte correlación positiva entre la temperatura media y el punto de rocío medio, con r = 0.962. La fuerza de las correlaciones de estas parcelas
(las seis en la parte inferior izquierda) se indica por el coeficiente de correlación en el panel correspondiente (espejado) en la parte superior derecha. También hay correlaciones negativas relativamente fuertes entre temperatura y presión, y punto de rocío y presión. En contraste, vemos correlaciones débiles entre humedad y temperatura y humedad y presión, como lo indican los valores bajos de r.

Lo importante a recordar de todo esto es lo que nos puede decir el coeficiente de correlación: una correlación alta y positiva entre dos variables indica que cuando una sube, también lo hace la otra. Una alta correlación negativa indica que a medida que uno sube, el otro baja. Coeficientes de correlación bajos indican que no se puede establecer una relación lineal consistente. Si se establece correlación, como nunca, este análisis aún no proporciona detalles sobre las relaciones funcionales presentes

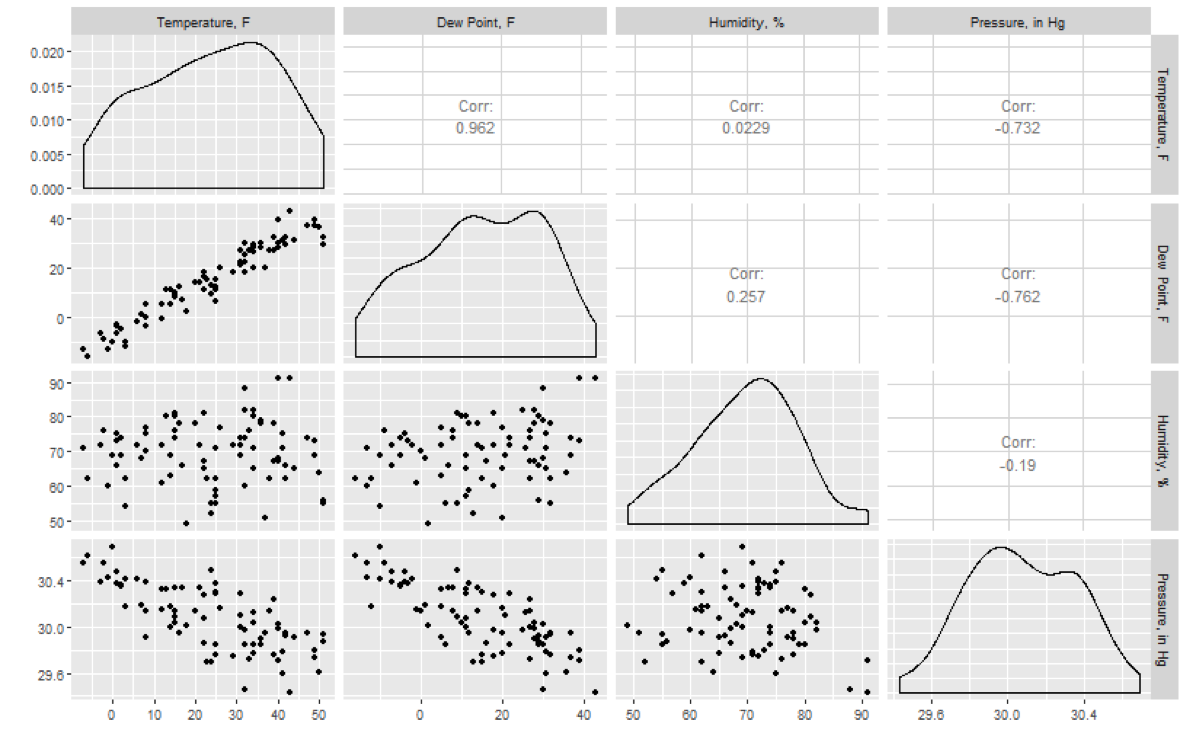
Figura 11.3: Parcelas de correlación para datos meteorológicos de Ames, IA, abril de 2014.

11.2 Regresión

La regresión es el proceso de ajustar una función matemática a un conjunto de puntos de datos utilizando algún criterio para juzgar “bondad de ajuste”. La función resultante de “mejor ajuste” se puede usar para predecir valores desconocidos, para pronosticar valores futuros o para evaluar la dependencia de una variable sobre otra. La bondad de ajuste se puede determinar mediante una de las muchas técnicas estadísticas que determinan qué tan bien describe una función las variaciones en los datos utilizados para generarla. El criterio más común para la bondad de ajuste se llama “mínimos cuadrados”, por lo que a veces puede ver todo el proceso llamado regresión de mínimos cuadrados. Mínimos cuadrados significa lo que suena, algo así como. Cuando se prueba una función (vamos a escribirla y = f (x)) para determinar la bondad de ajuste, la diferencia entre los valores y predichos por la función test, cada uno de los cuales podemos llamar y, en una x dada, y los valores y en el se encuentran, se encuentran al cuadrado y se suman para todo el conjunto de datos. La línea de mejor ajuste es entonces aquella para la que se minimiza (mínimo) la suma de los cuadrados de los residuos. Esto se hace muy comúnmente para ecuaciones lineales, pero también podemos usar las mismas técnicas para ecuaciones no lineales.

Sin embargo, algunos conjuntos de datos que podemos encontrar simplemente no parecen tener tendencias lineales. En estos casos, podemos intentar transformar una o ambas variables\(^{1}\) o podemos intentar realizar regresión no lineal. Al igual que con muchos de los métodos estadísticos y espaciales discutidos en este libro, el trabajo pesado para la mayoría de estas opciones puede -y probablemente debería- hacerse con software de computadora. Sin embargo, aún debemos estar al tanto de lo que está sucediendo

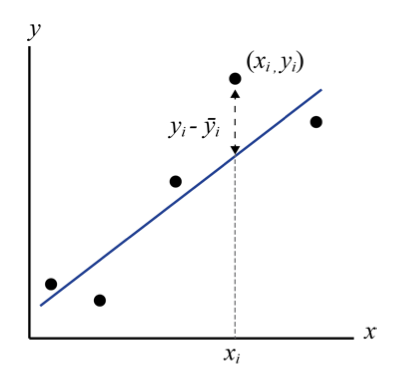
Figura 11.4: Representación esquemática de las cantidades involucradas en la búsqueda de funciones de mejor ajuste por regresión de mínimos cuadrados.

Elemento 1.

Algunas transformaciones de datos comunes incluyen logarítmica, exponencial y recíproca. En estas transformaciones, se crea una variable modificada realizando la operación seleccionada sobre los valores originales de la variable.

Capturas acumuladas	atrapar/esfuerzo
86	2.46
137	1.76
169	1.14
178	0.29

11.2.1 Ejemplo: pesca eléctrica de trucha de arroyo (Problema 3.7)

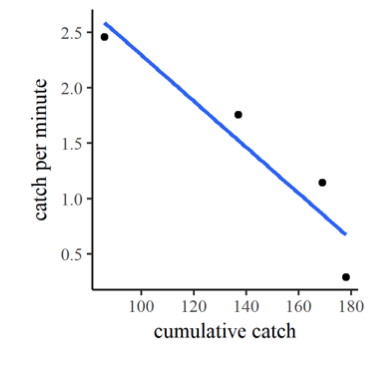
Figura 11.5: Captura por unidad de esfuerzo en función de la captura total para truchas de arroyo de edad 0, del Cuadro 11.2.1.

Después de haber aislado la trucha de arroyo de edad 0 de cada recorrido de electropesca y calculado la captura por unidad de esfuerzo c ue de ese subconjunto, ahora podemos emplear el método Leslie para estimar la población total de truchas de arroyo de edad 0 en el alcance del estudio.

En este método, creamos una variable dependiente c\(_{ccumul.}\) correspondiente al número acumulado de peces retirados en cada pasada, la “captura acumulativa”. Luego trazamos y realizamos una regresión lineal de la captura por unidad de esfuerzo en función de la captura acumulativa, como se ilustra en la Figura 11.5. Por el método de Leslie si extrapolamos la línea de mejor ajuste a un valor de eje vertical c\(_{ue}\) = 0, el valor de captura acumulativo donde eso ocurre es la población total estimada. Este valor se puede estimar a partir de la propia gráfica, pero el resultado es mejor si resolvemos el para el valor directamente desde la línea de mejor ajuste. La ecuación de la línea de mejor ajuste para esta regresión es:

c\(_{ue}\) = −0.0208\(_{ccumul.}\) + 4.38. (11.2)

Obsérvese que la pendiente de esta línea (−0.0208), consistente con la intuición, es un número negativo. La intersección y 4.38 corresponde a la hipotética captura inicial por unidad de esfuerzo al inicio mismo del primer recorrido. Reordenando y resolviendo para c\(_{ccumul.}\) da

c\(_{ccumul.}\) = 210.6 − 48.1\(_{cue}\) (11.3)

y encontramos que la población total estimada es de 210.

Ejercicio 1.

Discutir en un párrafo los beneficios e inconvenientes de decidir, antes de cualquier análisis de datos, para qué tipo de función buscar los parámetros más adecuados.

Ejercicio 2.

En la Sección 11.2.1, nos saltamos varios pasos en la manipulación algebraica que permitieron solución para c\(_{ccumul.}\) Llevar a cabo todos los pasos intermedios, mostrando su trabajo completamente, y determinar si la solución citada anteriormente es aceptable.

Ejercicio 3.

Encuentre un conjunto de datos que le interese dentro de un repositorio público de datos ecológicos o de recursos naturales\(^{2}\), identifique variables dentro de un conjunto de datos que puedan estar relacionadas y realice una regresión para ver la naturaleza de esa relación.

Elemento 2.

\(^{2}\)Por ejemplo, navegue por el Registro Global de Repositorios de Biodiversidad.