1.1: ¿Qué es el Orden?

Última actualización
Guardar como PDF

Page ID: 112189

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Arriba hablamos informalmente de dos conjuntos ordenados diferentes: el orden en la conectividad del sistema y el orden en booleanos false ≤ true. Entonces relacionamos estos dos conjuntos ordenados por medio de la observación de Alice Φ. Antes de continuar, necesitamos hacer esas ideas más precisas. Comenzamos en la Sección 1.2.1 con una revisión de conjuntos y relaciones. En la Sección 1.2.2 daremos la definición de un preorder—abreviatura de conjunto preordenado— y un buen número de ejemplos.

Revisión de conjuntos, relaciones y funciones

Aquí no vamos a dar una definición de conjunto, pero informalmente pensaremos en un conjunto como una colección de cosas, conocidas como elementos. Estas cosas podrían ser todas las hojas de un árbol determinado, o los nombres de tus frutas favoritas, o simplemente algunos símbolos a, b, c. Por ejemplo, escribimos A = {h ,1} para denotar el conjunto, llamado A, que contiene exactamente dos elementos, uno llamado h y otro llamado 1. El conjunto {h, h, 1, h, 1} es exactamente lo mismo que A porque ambos contienen los mismos elementos, h y 1, y repetir un elemento más de una vez en la notación no cambia el conjunto.3 Para un conjunto arbitrario X, escribimos x$\in$ X si x es elemento de X; entonces tenemos$h \in A$ y$1 \in A$, pero$0 \notin A$.

Ejemplo 1.9.

Aquí hay algunos conjuntos importantes de matemáticas-y la notación que usaremos- que volverán a aparecer en este libro.

$\varnothing$denota el conjunto vacío; no tiene elementos.
{1} denota un conjunto con un elemento; tiene un elemento, 1.
$\mathbb{B}$denota el conjunto de booleanos; tiene dos elementos, verdadero y falso.
$\mathbb{N}$denota el conjunto de números naturales; tiene elementos$0,1,2,3, \ldots, 90^{717}, \ldots$
$n,$para cualquiera$n \in \mathbb{N},$ denota el$n^{t h}$ ordinal; tiene$n$ elementos$1,2, \ldots, n .$ Por ejemplo,$\underline{0}=\varnothing, \underline{1}=\{1\},$ y$\underline{5}=\{1,2,3,4,5\}$
$\mathbb{Z},$el conjunto de enteros; tiene elementos$\ldots,-2,-1,0,1,2, \ldots, 90^{717}, \ldots$
$\mathbb{R},$el conjunto de números reales; tiene elementos como$\pi, 3.14,5 * \sqrt{2}, e, e^{2},-1457,90^{717},$ etc.

Dados los conjuntos X e Y, decimos que X es un subconjunto de Y, y escribimos X Y, si cada elemento en X también está en Y. Por ejemplo {h}$\subseteq$ A. Tenga en cuenta que el conjunto vacío Ø: = {} es un subconjunto de cada otro conjunto.4 Dado un conjunto Y y una propiedad P que es verdadera o falsa para cada elemento de Y, escribimos {y$\in$ Y | P (y)} para significar el subconjunto de aquellos y's que satisfacen a P.

Ejercicio 1.10.

¿Es cierto que N = {n$\in$ Z | n ≥ 0}?
¿Es cierto que N = {n$\in$ Z | n ≥ 1}?
¿Es cierto que Ø = {n$\in$ Z | 1 < n < 2}?

Si tanto X 1 como X 2 son subconjuntos de Y, su unión, denotada X 1 X 2, es también un subconjunto de Y, es decir, la que contiene los elementos en X1 y los elementos en X2 pero no más. Por ejemplo si Y = {1,2,3,4} y X 1 = {1,2} y X 2 = {2,4}, entonces X 1$\cup$ X 2 = {1,2,4}. Tenga en cuenta que Ø$\cup$ X = X para cualquier X$\subseteq$ Y.

De manera similar, si tanto X1 como X2 son subconjuntos de Y, entonces su intersección, denotada X 1$\cap$ X 2, es también un subconjunto de Y, es decir, la que contiene todos los elementos de Y que están ambos en X 1 y en X 2, y ninguna otra. Entonces {1,2,3}$\cap$ {2,5} = {2}.

¿Y si necesitamos unirnos o intersectar muchos subconjuntos? Por ejemplo, consideremos los conjuntos X 0 = Ø, X 1 = {1}, X 2 = {1,2}, etc. como subconjuntos de N, y queremos saber cuál es la unión de todos ellos. Esta unión está escrita$\cup$ n$\in$ N X n, y es el subconjunto de N que contiene cada elemento de cada X n, pero no otros. A saber,$\cup$ $\in$n N X n = {n$\in$ N | n ≥ 1}. De igual manera se puede escribir$\cap$ $\in$n N X n para la intersección de todas ellas, la cual estará vacía en el caso anterior.

Dados dos conjuntos X e Y, el producto X × Y de X e Y es el conjunto de pares (x, y), donde x$\in$ X e y $\in$Y.

Por último, tal vez queramos tomar una unión disjunta de dos conjuntos, aunque tengan elementos en común. Dados dos conjuntos X e Y, su unión disjunta X$\sqcup$ Y es el conjunto de pares de la forma (x, 1) o (y, 2), donde x$\in$ X e y $\in$Y.

Ejercicio 1.11.

Sea A = {h, 1} y B = {1, 2, 3}.

Hay ocho subconjuntos de B; escríbelos.
Toma cualquiera de dos subconjuntos no vacíos de B y escribe su unión.
Hay seis elementos en A × B; escríbelos. ♦
Hay cinco elementos de A$\cup$ B; escríbelos.
Si consideramos A y B como subconjuntos del conjunto {h, 1, 2, 3}, hay cuatro elementos de A$\cup$ B; escríbelos.

Las relaciones entre diferentes conjuntos, por ejemplo, entre el conjunto de árboles en tu vecindario y el conjunto de tus frutas favoritas se capturan usando subconjuntos y conjuntos de productos.

Definición: 1.12.

Deja que X e Y sean conjuntos. Una relación entre X e Y es un subconjunto R$\subseteq$ X × Y. Una relación binaria en X es una relación entre X y X, es decir, un subconjunto R$\subseteq$ X × X.

Es conveniente usar algo llamado notación infijo para las relaciones binarias R$\subseteq$ A × A.

Esto significa que uno elige un símbolo, digamos ⋆, y escribe a ⋆ b para significar (a, b)$\in$ R.

Ejemplo 1.13.

Hay una relación binaria en R con notación de infijo ≤. En lugar de escribir (5, 6)$\in$ R, escribimos 5 ≤ 6. Otros ejemplos de notación infija para las relaciones son =, ≈, <, >. En teoría de números, les interesa si un número divide sin resto en otro número; esta relación se denota con notación infija |, entonces 5|10.

Particiones y relaciones de equivalencia. Ahora podemos definir particiones de manera más formal.

Definición: 1.14.

Si A es un conjunto, una partición de A consiste en un conjunto P y, por cada p$\in$ P, un subconjunto no vacío A p$\subseteq$ A, tal que

(1.15)

Podemos denotar la partición por {A p} $\in$p P. Nos referimos a P como el conjunto de etiquetas de pieza y si p$\in$ P es una etiqueta de parte, nos referimos a A p como la$^{th}$ parte p. La condición (1.15) dice que cada elemento a ∈ A está exactamente en una parte. Consideramos que dos particiones diferentes {$\left\{A_{p}\right\}_{p \in P}$$\left\{A_{p^{\prime}}^{\prime}\right\}_{p^{\prime} \in P^{\prime}}$} y {} de A son iguales si por cada p$\in$ P existe un p'$\in$ P' con$A_{p}$ =$A'_{p'}$,. Es decir, si dos formas de dividir A en partes son exactamente las mismas el único cambio está en las etiquetas entonces no hacemos distinción entre ellas.

Ejercicio 1.16.

Supongamos que A es un conjunto y {$A_{p}$} $\in$p P y {$\left\{A_{p^{\prime}}^{\prime}\right\}_{p^{\prime} \in P^{\prime}}$} son dos particiones de

A tal que por cada p$\in$ P existe un p ′$\in$ P' con$A_{p}$ =$A′_{p′}$,.

Mostrar que por cada p$\in$ P hay como máximo un p ′$\in$ P ′ tal que$A_{p}$ =$A′_{p′}$
Mostrar que por cada p ′$\in$ P ′ hay un p$\in$ P tal que$A_{p}$ =$A′_{p′}$,.

Ejercicio 1.17.

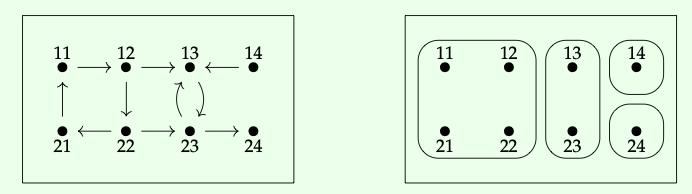
Considere la partición que se muestra a continuación:

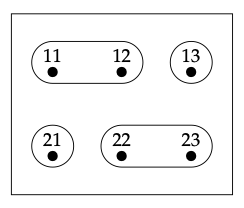
$Screen Shot 2021-01-04 en 3.54.08 PM.png$

Contestar: Para dos elementos cualesquiera a, b$\in$ {11,12,13,21,22,23}, vamos a permitirnos escribir un símbolo de twiddle a ∼ b entre ellos si a y b están ambos en la misma parte. Anote cada par de elementos (a, b) que estén en la misma parte. Debe haber 10.5 ♦

Veremos en la Proposición 1.19 que existe una fuerte relación entre particiones y algo llamado relaciones de equivalencia, que definimos a continuación.

Definición 1.18: Reflexividad, Simetría y Transitividad

Que A sea un conjunto. Una relación de equivalencia en A es una relación binaria, vamos a darle notación de infijo ∼, satisfaciendo las siguientes tres propiedades:

a ∼ a, para todos a$\in$ A,
a ∼ b$iff_{a}$ b ∼ a, para todos a, b$\in$ A, y
si a ∼ b y b ∼ c entonces a ∼ c, para todos a, b, c.$\in$ A.

Estas propiedades se denominan reflexividad, simetría y transitividad, respectivamente.

'Iff' es la abreviatura de 'si y sólo si'.

Proposición 1.19.

Que A sea un conjunto. Existe una correspondencia uno a uno entre las formas de particionar A y las relaciones de equivalencia en A.

Prueba. Primero mostramos que cada partición da lugar a una relación de equivalencia, y luego que cada relación de equivalencia da lugar a una partición. Nuestras dos construcciones serán mutuamente inversas, demostrando la proposición.

Supongamos que se nos da una partición {$\left\{A_{p}\right\}_{p \in P}$}; definimos una relación ∼ y mostramos que es una relación de equivalencia. Definir a ∼ b para significar que a y b están en la misma parte: hay algo de p$\in$ P tal que a$\in$$A_{p}$ y b$\in$$A_{q}$. Es obvio que a está en la misma parte que él mismo. De igual manera, es obvio que si a está en la misma parte que b entonces b está en la misma parte que a, y que si más b está en la misma parte que c entonces a está en la misma parte que c. Así ∼ es una relación de equivalencia como se define en la Definición 1.18.

Supongamos que dada una relación de equivalencia ∼; formaremos una partición en A diciendo cuáles son las partes. Digamos que un subconjunto X$\subseteq$ A es (∼) -cerrado si, por cada $\in$x X y x ′ ∼ x, tenemos $\in$x ′ X. Digamos que un subconjunto X$\subseteq$ A está (∼) -conectado si no está vacío y x ∼ y para cada x, y$\in$ X. Entonces las partes correspondientes a ∼ son exactamente los subconjuntos (∼) -cerrados, (∼) -conectados. No es difícil comprobar que estos de hecho forman una partición. □

Ejercicio 1.20.

Completemos la parte de “no es difícil de verificar” en la prueba de la Proposición 1.19. Supongamos que ∼ es una relación de equivalencia en un conjunto A, y deja que P sea el conjunto de subconjuntos (∼) -cerrado y (∼) -conectado {$\left\{A_{p}\right\}_{p \in P}$}.

Demuestre que cada parte no$A_{p}$ está vacía.
Mostrar que si p$\neq$ q, es decir, si$A_{p}$ y no$A_{q}$ son exactamente el mismo conjunto,$A_{p}$ entonces$A_{q}$ = Ø.
Mostrar que A =$\cup$ $\in$p$A_{p}$ P. ♦

Definición: 1.21.

Dado un conjunto A y una relación de equivalencia ∼ sobre A, decimos que el cociente A /∼ de A bajo ∼ es el conjunto de partes de la partición correspondiente.

Funciones. El tipo de relación más utilizado entre conjuntos es el de funciones.

Definición: 1.22.

Deja que S y T sean conjuntos. Una función de S a T es un subconjunto F$subseteq$ S × T tal que para todos los $\in$s S existe una t$\in$ T única con (s, t)$\in$ F.

La función F a menudo se denota F: S → T. A partir de ahora, escribimos F (s) = t, o a veces s → t, para significar (s, t)$\in$ F. Para cualquier t$\in$ T, la preimagen de t a lo largo de F es el subconjunto {$\in$s S | F (s) = t}.

Una función se llama suryectiva, o una sobreyección, si para todo t ∈ T existe s$\in$ S con F (s) = t. Una función se llama inyección, o inyección,

si para todos t$\in$ T y s 1, s 2$\in$ S con F (s 1) = t y F (s 2) = t, tenemos s 1 = s 2. Una función se llama biyectiva si es tanto suryectiva como inyectora.

Utilizamos diversas decoraciones en flechas,para denotar este tipo especial de funciones. Aquí hay una tabla con el nombre, decoración de flechas y un ejemplo de cada tipo de función:

función arbitraria función suryectiva función inyectiva función biyectiva

$Screen Shot 2021-01-05 at 7.57.43 PM.png$

Ejemplo 1.23.

Un tipo de función importante pero muy simple es la función de identidad en un conjunto X, denotada id X. Es la función biyectiva id X (x) = x.

Para la consistencia notacional con la Definición 1.22, las flechas del Ejemplo 1.23 podrían dibujarse como → en lugar de —>. Las flechas de estilo —>- fueron dibujadas porque pensamos que era más bonita, es decir, más fácil a la vista. La belleza también es importante; una preferencia desequilibrada por la corrección estricta sobre la belleza se convierte en pedantería. Pero fuera de las fotos, vamos a tener cuidado.

Ejercicio 1.24.

En lo siguiente, no utilice ningún ejemplo ya dibujado anteriormente.

Encuentra dos conjuntos A y B y una función f: A → B que sea inyectiva pero no suryectiva.
Encuentra dos conjuntos A y B y una función f: A → B que sea suryectiva pero no inyectiva.

Consideremos ahora las cuatro relaciones que se muestran aquí:

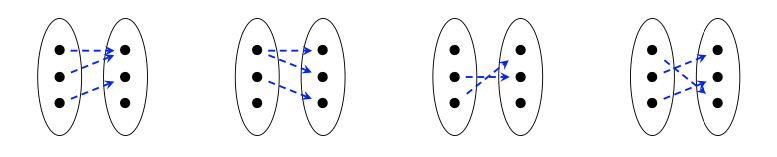
$Screen Shot 2021-01-04 a las 5.27.59 PM.png$

o cada relación, conteste las dos preguntas siguientes.

3. ¿Es una función?

4. Si no, ¿por qué no? Si es así, ¿es inyectable, suryectiva, ambas (es decir, biyectiva), o ninguna? ♦

Ejercicio 1.25.

Supongamos que A es un conjunto y f: A → Ø es una función para el conjunto vacío. Demuestre que A está vacía.

Ejemplo 1.26.

Una partición en un conjunto A también se puede entender en términos de funciones suryectivas fuera de A. Dada una función suryectiva f: A —” P, donde P es cualquier otro conjunto, las preimágenes f −1 (p)$\subseteq$ A, una por cada elemento $\in$p P, forman una partición de A. Aquí hay un ejemplo.

Considere la partición de S: = {11, 12, 13, 21, 22, 23} que se muestra a continuación:

Se ha dividido en cuatro partes, así que vamos a P = {a, b, c, d} y dejar que f: S —” P sean dadas por

f (11) = a, f (12) = a, f (13) = b, f (21) = c, f (22) = d, f (23) = d

Ejercicio 1.27.

Anote una sobrejección correspondiente a cada una de las cinco particiones en la Ec. (1.5) . ♦

Definición: 1.28.

Si F: X → Y es una función y G: Y → Z es una función, su compuesto es la función X → Z definida como G (F (x)) para cualquier x $\in$X. A menudo se denota G ◦ F, pero preferimos denotarlo F; G. Toma cualquier elemento x$\in$ X, evalúa F para obtener un elemento F (x)$\in$ Y y luego evalúa G para obtener un elemento G (F (x)).

Ejemplo 1.29.

Si X es cualquier conjunto y x$\in$ X es cualquier elemento, podemos pensar en x como una función {1} → X, es decir, la función que envía 1 a x. Por ejemplo, las tres funciones {1} → {1, 2, 3} que se muestran a continuación corresponden a los tres elementos de {1, 2, 3}:

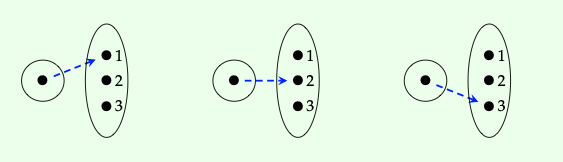
$Screen Shot 2021-01-06 en 1.21.35 PM.png$

Supongamos que se le da una función F: X → Y y un elemento de X, pensado como una función x: {1} → X. Después la evaluación de F en x viene dada por el compuesto, F (x) = x; F.

Pedidos por adelantado

En la Sección 1.1, utilizamos varias veces el símbolo ≤ para denotar una especie de orden. Aquí hay una definición formal de lo que significa que un conjunto tenga un orden.

Definición: 1.30.

Una relación de preorden en un conjunto X es una relación binaria en X, aquí denotada con notación de infijo ≤, tal que

(a) x ≤ x; y

(b) si x ≤ y e y ≤ z, entonces x ≤ z.

La primera condición se llama reflexividad y la segunda se llama transitividad. Si x ≤ y y ≤ x, escribimos x$\cong$ y decimos x e y son equivalentes. Llamamos a un par (X, ≤) que consiste en un conjunto equipado con una relación de preorden un preorder.

OBSERVACIÓN 1.31. Observe que la reflexividad y la transitividad son familiares a partir de la Definición 1.18: los preordenes son solo relaciones de equivalencia sin la condición de simetría.

Ejemplo 1.32 (Preordenes discretos).

Cada conjunto X puede considerarse como un preorden discreto (X, =). Esto significa que las únicas relaciones de orden en X son de la forma x ≤ x; si x$\neq$ y entonces ni x ≤ y ni ni ≤ x hold.

Describimos los pedidos por adelantado discretos como simplemente una colección de puntos:

$Screen Shot 2021-01-06 at 1.28.07 PM.png$

Ejemplo 1.33 (Preordenes codiscretos).

A partir de cada conjunto también podemos construir su preorden codiscreto (X, ≤) equipándolo con la relación binaria total X × $\subseteq$X X × X. Esta es una estructura muy trivial: significa que para todos x e y en X tenemos x ≤ y (y por lo tanto también y ≤ x).

Ejemplo 1.34 (Booleanos).

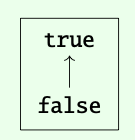
Los booleanos$\mathbb{B}$ = {false, true} forman un preorder con false ≤ true.

$Screen Shot 2021-01-06 at 1.31.30 PM.png$

Observación 1.35 (Los pedidos parciales son preordenes esqueléticos). Un pedido por adelantado es un pedido parcial si además tenemos eso

(c) x$\cong$ y implica x = y.
En la terminología de teoría de categorías, el requisito de que x$\cong$ y implica x = y se conoce como esqueletalidad, por lo que los órdenes parciales son preordenes esqueléticos. Para abreviar, también usamos el término poset, una contracción de conjunto parcialmente ordenado.

La diferencia entre preordenes y parciales es bastante menor. Una orden parcial ya es una preorden, y cada preorden se puede hacer en un orden parcial equiparando cualesquiera dos elementos x, y para los cuales x$\cong$ y, es decir, para los cuales x ≤ y e y ≤ x.

Por ejemplo, cualquier preorden discreto ya es un orden parcial, mientras que cualquier preorden codiscreto simplemente se convierte en el orden parcial único en un conjunto de elementos.

Ya hemos introducido algunos ejemplos de preordenes usando diagramas de Hasse. Será conveniente seguir haciendo esto, así que seamos un poco más formales sobre lo que queremos decir. Primero, necesitamos definir una gráfica.

Definición: 1.36.

Una gráfica G = (V, A, s, t) consiste en un conjunto V cuyos elementos se denominan vértices, un conjunto A cuyos elementos se llaman flechas, y dos funciones s,

t: A → V conocidas como las funciones fuente y destino respectivamente. Dada $\in$una A con s (a) = v y t (a) = w, decimos que a es una flecha de v a w.

Por un camino en G nos referimos a cualquier secuencia de flechas tal que el objetivo de una flecha sea la fuente de la siguiente. Esto incluye secuencias de longitud 1, que son solo flechas a $\in$A en G, y secuencias de longitud 0, que apenas comienzan y terminan en el mismo vértice v, sin atravesar ninguna flecha.

Ejemplo 1.37.

Aquí hay una imagen de una gráfica:

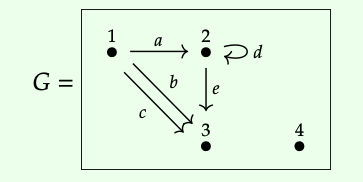
$Screen Shot 2021-01-06 en 1.33.56 PM.png$

Tiene V = {1, 2, 3, 4} y A = {a, b, c, d, e}. Las funciones fuente y destino, s, t: A → V vienen dadas por las siguientes tablas parcialmente rellenadas (ver Ejercicio 1.38):

$Screen Shot 2021-01-06 at 1.34.42 PM.png$

Hay un camino de 2 a 3, es decir, la flecha e es un camino de longitud 1. No hay caminos de 4 a 3, pero hay un camino de 4 a 4, es decir, el camino de longitud 0. Hay infinitamente muchos caminos 1 → 2 porque uno puede bucle y bucle y bucle a través de d tantas veces como le plazca.

Ejercicio 1.38.

Rellene la tabla del Ejemplo 1.37. ♦

OBSERVACIÓN 1.39. De cada gráfica podemos obtener una preorden. En efecto, un diagrama de Hasse es una gráfica G = (V, A, s, t) que da una presentación de un preorden (P, ≤). Los elementos de P son los vértices V en G, y el orden ≤ viene dado por v ≤ w iff hay una ruta v → w. Para cualquier vértice v, siempre hay un camino v → v, y esto se traduce en la ley de reflexividad de la Definición 1.30. El hecho de que los caminos u → v y v → w puedan ser concatenados a un camino u → w se traduce en la ley de transitividad.

Ejercicio 1.40.

¿Qué relación de preorden (P, ≤) es representada por la gráfica G en el Ejemplo 1.37? Es decir, cuáles son los elementos de P y anotar cada par (p 1, p 2) para el cual p 1 ≤ p 2. ♦

Ejercicio 1.41.

¿Un conjunto de puntos, como el del Ejemplo 1.32, cuenta como diagrama de Hasse? ♦

Ejercicio 1.42.

Sea X el conjunto de particiones de {•, ◦, ∗}; tiene cinco elementos y un orden por la tosquedad, como se muestra en el diagrama de Hasse Eq. (1.5). Anote cada par (x, y) de elementos en X de tal manera que x ≤ y. Debe haber 12. ♦

OBSERVACIÓN 1.43. En Observación 1.35 discutimos órdenes parciales preordenes con la propiedad que siempre que dos elementos son equivalentes, son iguales y luego dijimos que esta propiedad es bastante intrascendente: cualquier preorden puede convertirse a un orden parcial que sea categoría “equivalente” teóricamente. Una orden parcial es como una preorden con un corte de pelo elegante: algunos matemáticos tal vez ni siquiera se den cuenta.

No obstante, existen otros tipos de preordenes que son más especiales y notables. Por ejemplo, un pedido total tiene la siguiente propiedad adicional:

(d) para todos x, y, ya sea x ≤ y o y ≤ x.
Decimos que dos elementos x, y de un preorden son comparables si x ≤ y o y ≤ x, por lo que un orden total es un preorden donde cada dos elementos son comparables.

Ejemplo 1.44.

¿Es correcto decir que un preorden discreto es aquel en el que no hay dos elementos comparables?

Ejemplo 1.45 (Números naturales).

Los números naturales$\mathbb{N}$ := {0, 1, 2, 3,.} son un pre- orden con el orden dado por el orden de tamaño habitual, por ejemplo 0 ≤ 1 y 5 ≤ 100. Este es un orden total: ya sea m ≤ n o n ≤ m para todos m, n. Se puede ver que su diagrama de Hasse se parece a una línea:

$Screen Shot 2021-01-06 en 1.39.17 PM.png$

Lo que hizo que la Eq. (1.5) no pareciera una línea es que hay elementos no comparables a y b —es decir, todos aquellos en la fila media. que no satisfacen ni a ≤ b ni b ≤ a.

Tenga en cuenta que para cualquier conjunto S, hay muchas formas diferentes de asignar una orden a S. En efecto, para el conjunto N, también podríamos usar el orden discreto: solo escribir n ≤ m si n = m. Otro orden es el orden inverso, como 5 ≤ 3 y 3 ≤ 2, como la forma en que se anota el golf (5 es peor que 3).

Otro orden más$\mathbb{N}$ está dado por división: decimos que n ≤ m si n se divide en m sin resto. En este orden 2 ≤ 4, por ejemplo, pero 2$\neq$ 3, ya que hay un resto cuando 2 se divide en 3.

Ejercicio 1.46.

Anota los números 1,2,... ,10 y dibuja una flecha a → b si a se divide perfectamente en b. ¿Es un pedido total? ♦

Ejemplo 1.47 (Números reales).

Los números reales$\mathbb{R}$ también forman un preorden con el “orden habitual”, por ejemplo −500 ≤ −499 ≤ 0 ≤ √2 ≤ 100/3.

Ejercicio 1.48.

¿El habitual ≤ ordenar en el conjunto$\mathbb{R}$ de números reales es un pedido total? ♦

Ejemplo 1.49 (Partición de preorden).

Dado un preorden, es decir, un conjunto preordenado (P, ≤), definimos la noción de equivalencia de elementos, denotada x$\cong $ y, para significar x ≤ y e y ≤ x. Esta es una relación de equivalencia, por lo que induce una partición en P. (La frase “A induce a B” significa que tenemos una forma automática de convertir una A en una B. En este caso, estamos diciendo que tenemos una forma automática de convertir las relaciones de equivalencia en particiones, lo cual hacemos; ver Proposición 1.19.)

Por ejemplo, el preorden cuyo diagrama de Hasse se dibuja a la izquierda corresponde a la partición dibujada a la derecha.

$Screen Shot 2021-01-06 en 1.46.12 PM.png$

Ejemplo 1.50 (Power set).

Dado un conjunto X, el conjunto de subconjuntos de X se conoce como el conjunto de potencia de X; lo denotamos P (X). Naturalmente, al conjunto de potencias se le puede dar un orden mediante la inclusión de subconjuntos (y a partir de ahora, siempre que hablemos del conjunto de potencia como un conjunto ordenado, este es el orden que queremos decir).

Por ejemplo, tomando X = {0, 1, 2}, representamos P (X) como

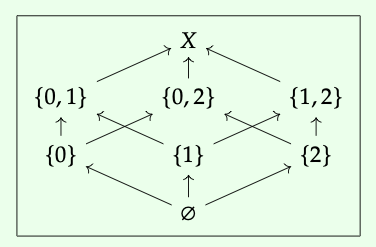
$Screen Shot 2021-01-06 a las 2.10.41 PM.png$

¿Ves el cubo? El diagrama de Hasse para el conjunto de potencias de un conjunto finito, digamos P {1, 2,.., n},$^{a}$ siempre parece un cubo de dimensión n.

$^{a}$Tenga en cuenta que aquí omitimos los paréntesis, escribiendo P X en lugar de P (X); a lo largo de este libro omitiremos paréntesis si juzgamos que la presentación es más limpia y es poco probable que cause confusión.

Ejercicio 1.51.

Dibuja los diagramas de Hasse para P (Ø), P {1} y P {1, 2} . ♦

Ejemplo 1.52 (Particiones).

Hablamos de obtener una partición de un preorden; ahora pensemos en cómo podríamos ordenar el conjunto Prt (A) de todas las particiones de A, para algún conjunto A. De hecho, lo hemos hecho antes en la Ec. (1.5). A saber, ordenamos en particiones por finura: una partición P es más fina que una partición Q si, por cada parte p$\in$ P hay una parte q ∈ Q tal que Ap $\subseteq$A q. También podríamos decir que Q es más grosera que P.

Recordemos del Ejemplo 1.26 que las particiones en A pueden considerarse como funciones suryectivas fuera de A. Entonces f: A —” P es más fino que g: A —” Q si hay una función h: P → Q tal que f; h = g.

Ejercicio 1.53.

Para cualquier conjunto S hay una partición más basta, teniendo solo una parte. ¿A qué función suryectiva corresponde? También hay una mejor partición, donde todo está en su propia partición. ¿A qué función suryectiva corresponde? ♦

Ejemplo 1.54 (Conjuntos superiores).

Dado un preorden (P, ≤), un conjunto superior en P es un subconjunto U de P que satisface la condición de que si p$\in$ U y p ≤ q, entonces q$\in$ U. “Si p es un elemento entonces también lo es algo más grande”. Escriba U (P) para el conjunto de conjuntos superiores en P. Podemos darle una orden al conjunto U dejando que U ≤ V si U está contenido en V.

Por ejemplo, si ($\mathbb{B}$, ≤) son los booleanos (Ejemplo 1.34), entonces su preorden de valores superiores$\cup$ ($\mathbb{B}$) es

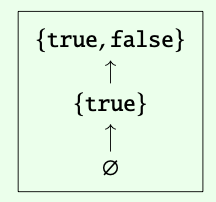
$Screen Shot 2021-01-06 en 2.33.49 PM.png$

El subconjunto {false} no$\subseteq$$\mathbb{B}$ es un conjunto superior, porque false ≤ true y true$\not in$ {false}.

Ejercicio 1.55.

Demostrar que el preorden de los conjuntos superiores en un preorden discreto (ver Ejemplo 1.32) en un conjunto X es simplemente el conjunto de potencia P (X) . ♦

Ejemplo 1.56 (Preorden de producto).

Dados los pedidos anticipados (P, ≤) y (Q, ≤), podemos definir una estructura de preorden en el conjunto de productos P × Q estableciendo (p, q) ≤ (p ′, q ′) si y solo si p ≤ p ′ y q ≤ q ′. A esto lo llamamos el prepedido del producto. Este es un ejemplo básico de una construcción más general conocida como el producto de categorías.

Ejercicio 1.57.

Dibuja el diagrama de Hasse para el producto de los dos prepedidos dibujados a continuación:

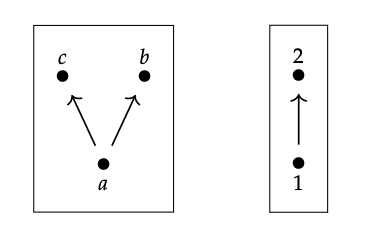
$Screen Shot 2021-01-04 a las 5.49.06 PM.png$: Para puntos de bonificación, compute el preorden del conjunto superior en el resultado. ♦

Ejemplo 1.58 (Preorden opuesto).

Dado un preorden (P, ≤), podemos definir el preorden opuesto (P, ≤$^{op}$) para tener el mismo conjunto de elementos, pero con (p ≤$^{op}$) q si y solo si q ≤ p.

Mapas de Monotone

Nosotros hemos dicho que la perspectiva categórica enfatiza las relaciones entre las cosas. Por ejemplo, un preorden es un entorno o mundo en el que tenemos un tipo de relación, ≤, y dos objetos cualesquiera pueden estar, o no, así relacionados. Saltando un nivel, la perspectiva categórica enfatiza que los preordenes a sí mismos cada uno un mundo en miniatura compuesto de muchas relaciones pueden relacionarse entre sí.

El tipo de relación más importante entre los pedidos por adelantado se llama mapa monótona. Estas son funciones que preservan las relaciones de preorden en algún sentido mapeos que respetan ≤ y por lo tanto se consideran la noción correcta de mapa de preservación de estructura para preordenes.

Definición: 1.59.

Un mapa monótono entre preordenes (A, ≤ A) y (B, ≤ B) es una función f: A → B tal que, para todos los elementos x, y$\in$ A, si x ≤ A y luego f (x) ≤ B f (y).

Un mapa monótona A → B entre dos preordenes asocia a cada elemento de preorden A un elemento del preorden B. Lo representamos dibujando una flecha punteada desde cada elemento x$\in$ A hasta su imagen f (x)$\in$ B. Tenga en cuenta que el orden debe conservarse para poder contar como un mapa monótono válido, por lo que si el elemento x está por encima del elemento y en el preorden izquierdo A, entonces la imagen f (x) estará por encima de la imagen f (y) en el preorden de derecha.

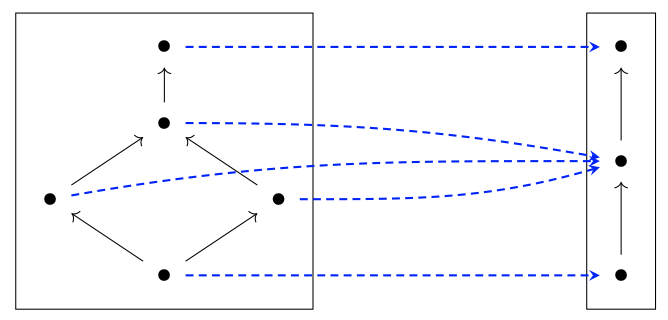
$Screen Shot 2021-01-04 at 5.53.21 PM.png$

Ejemplo 1.60.

Dejar$\mathbb{B}$ y$\mathbb{N}$ ser los preordenes de booleanos del Ejemplo 1.34 y N el preorden de los números naturales del Ejemplo 1.45. El mapa$\mathbb{B}$ →$\mathbb{N}$ enviar falso a 17 y verdadero a 24 es un mapa monótono, porque conserva el orden.

$Screen Shot 2021-01-06 en 2.51.59 PM.png$

Ejemplo 1.61 (El árbol de la vida).

Considera el conjunto de todas las clasificaciones de animales, por ejemplo 'tigre', 'mamífero', 'sapiens', 'carnívoro', etc. Estos están ordenados por especificidad: dado que 'tigre' es un tipo de 'mamífero', escribimos tigre ≤ mamífero. El resultado es un preorden, que de hecho forma un árbol, a menudo llamado el árbol de la vida. En la parte superior del siguiente diagrama vemos una pequeña parte del mismo:

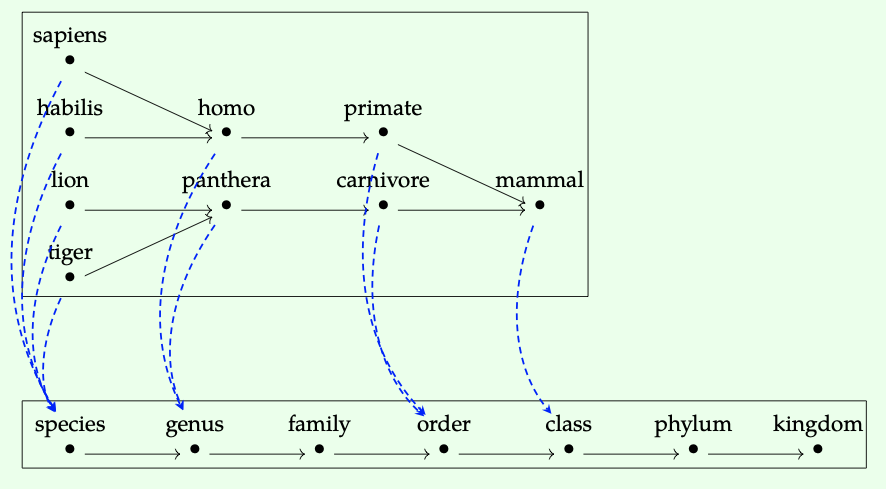
$Screen Shot 2021-01-06 en 2.54.20 PM.png$

En la parte inferior vemos la estructura jerárquica como un preorden. Las flechas discontinuas muestran un mapa monótona, llamarlo F, desde las clasificaciones hasta la jerarquía. Es monótona porque conserva el orden: siempre que haya un camino x → y arriba, hay un camino F (x) → F (y) abajo.

Ejemplo 1.62.

Dado un conjunto finito X, recuerde el conjunto de potencia P (X) y su relación de orden natural del Ejemplo 1.50. El mapa |·|: P (X) →$\mathbb{N}$ enviando cada subconjunto S a su número de elementos | S |, también llamado su cardinalidad, es un mapa monótona.

Ejercicio 1.63.

Dejar X = {0, 1, 2}.

Dibuja el diagrama de Hasse para P (X).
Dibuja el diagrama de Hasse para el preorden 0 ≤ 1 ≤ 2 ≤ 3.
Dibuja el mapa de cardinalidad |·| del Ejemplo 1.62 como líneas discontinuas entre ellos. ♦

Ejemplo 1.64.

Recordemos la noción de conjunto superior del Ejemplo 1.54. Dado un preorden (P, ≤), el mapa U (P) → P (P) que envía cada conjunto superior de (P, ≤) a sí mismo, considerado como un subconjunto de P, es un mapa monótona.

Ejercicio 1.65.

Considera el preorden B. El diagrama de Hasse para U ($\mathbb{B}$) se dibujó en el Ejemplo 1.54, y usted dibujó el diagrama de Hasse para P ($\mathbb{B}$) en el Ejercicio 1.51. Ahora dibuja el mapa monótona entre ellos, como se describe en el Ejemplo 1.64.

Ejercicio 1.66.

Sea (P, ≤) un preorden, y recuerde la noción de preorden opuesto del Ejemplo 1.58.

Mostrar que el conjunto ↑ p: = {p ′$\in$ P | p ≤ p ′} es un conjunto superior, para cualquier $\in$p P.
Mostrar que esta construcción define un mapa monótona ↑: P$^{op}$ → U (P).
Mostrar que si p ≤ p ′ en P si y sólo si ↑ (p ′)$\subseteq$ ↑ (p).
Dibuja una imagen del mapa ↑ en el caso en que P sea el pre orden (b ≥ a ≤ c) del Ejemplo 1.56.

Esto se conoce como el lema de Yoneda para los pedidos por adelantado. La condición si y sólo si probada en la parte 3 implica que, hasta la equivalencia, conocer un elemento es lo mismo que conocer su conjunto superior, es decir, conocer su red de relaciones con los demás elementos del preorden. El lema general de Yoneda es una poderosa herramienta en la teoría de categorías, y además una idea filosófica fascinante. ♦

Ejercicio 1.67.

Como usted mismo bien sabe, un mapa monótono f: (P, ≤ P) → (Q, ≤ Q) consiste en una función f: P → Q que satisface una propiedad de “monotonicidad”. Mostrar que cuando (P, ≤ P) es un preorden discreto, entonces cada función P → Q satisface la propiedad de monotonicidad, independientemente del orden ≤ Q

Ejemplo 1.68.

Recordemos del Ejemplo 1.52 que dado un conjunto X definimos Prt (X) para que sea el conjunto de particiones en X, y que una partición puede definirse usando una función surjectiva s: X —” P para algún conjunto P. Cualquier función suryectiva f: X —” Y induce un mapa monótona f$^{*}$: Prt (Y) → Prt (X), yendo “hacia atrás”. Se define enviando una partición s: Y —” P al compuesto f; s: X —” P. $^{7}$

Ejercicio 1.69.

Elija dos conjuntos X e Y con al menos tres elementos cada uno y elija una función suryectiva, no identitaria f: X —” Y entre ellos. Anote dos particiones diferentes P y Q de Y, y luego encuentre f$^{*}$ (P) y f$^{*}$ (Q) . ♦

La siguiente proposición, la Proposición 1.70, es sencilla de verificar. Recordemos la definición de la función de identidad del Ejemplo 1.23 y la definición de composición de la Definición 1.28.

Proposición 1.70.

Para cualquier preorden (P, ≤ P), la función de identidad es monótona. Si (Q, ≤ Q) y (R, ≤ R) son preordenes y f: P → Q y g: Q → R son monótonos, entonces (f; g): P → R también es monótona.

Ejercicio 1.71.

Verifique las dos afirmaciones hechas en la Proposición 1.70. ♦

Ejemplo 1.72.

Recordemos nuevamente la definición de preorden opuesto del Ejemplo 1.58. La función de identidad id P: P → P es un mapa monótono (P, ≤) → (P, ≤$^{op}$) si y solo si para todos p, q$\in$ P tenemos q ≤ p siempre que p ≤ q. Por razones históricas conectadas al álgebra lineal, cuando esto es cierto, llamamos (P, ≤) un preorden de daga.

Pero, de hecho, hemos visto antes pedidos por adelantado de dagas con otra apariencia. En efecto, si (P, ≤) es un preorden de daga, entonces la relación ≤ es simétrica: p ≤ q si y solo si q ≤ p, y también es reflexiva y transitiva por definición de preorden. Entonces, de hecho ≤ es una relación de equivalencia (Definición 1.18).

Ejercicio 1.73.

Recordemos la noción de preordenes esqueléticos (Observación 1.35) y preordenes discretos (Ejemplo 1.32). Demuestre que un preorden de daga esquelética es solo un preorden discreto, y por lo tanto se puede identificar con un conjunto. ♦

OBSERVACIÓN 1.74. Decimos que una A “se puede identificar con” a B cuando cualquier A nos da una B única y cualquier B nos da una A única, y ambos viajes de ida y vuelta de una A a una B y de regreso a una A, o de a B a una A y de vuelta a una B nos devuelven a donde empezamos. Por ejemplo, cualquier preorden discreto (P, ≤) tiene un conjunto subyacente P, y cualquier conjunto P se puede convertir en un preorden discreto (p 1 ≤ p 2 iff p 1 = p 2), y los viajes de ida y vuelta nos devuelven a donde empezamos. Entonces, ¿cuál es la diferencia? Es como la noción de permanencia de objetos desde la jerga del desarrollo infantil: podemos reconocer “la misma silla, simplemente movida de una habitación a otra”. Una silla en la habitación de juegos se puede mover a una silla en la sala de pedidos por adelantado. La iluminación es diferente pero la silla es la misma.

Eventualmente, podremos entender esta noción en términos de equivalencia de categorías, que están relacionadas con isomorfismos, que exploraremos a continuación en la Definición 1.75.

Definición: 1.75.

Dejar que (P, ≤ P) y (Q, ≤ Q) sean pedidos por adelantado. Una función monótona f: P → Q se denomina isomorfismo si existe una función monótona g: Q → P tal que f; g$id_{P}$ y g; f $id_{Q}$. Esto significa que para cualquier p$\in$ P y q$\in$ Q, tenemos p = g (f (p)) y q = f (g (q)). Nos referimos a g como la inversa de f, y viceversa: f es la inversa de g. Si hay un isomorfismo P → Q, decimos que P y Q son isomórficos.

Un isomorfismo entre preordenes es básicamente solo un relabeling de los elementos.

Ejemplo 1.76.

Aquí están los diagramas de Hasse para tres preordenes P, Q y R, todos los cuales son isomórficos:

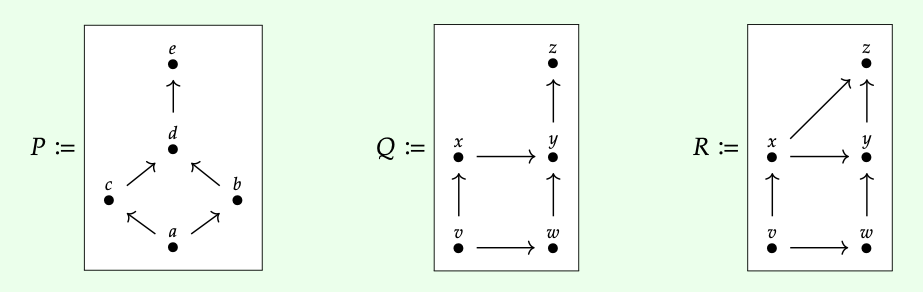
$Screen Shot 2021-01-06 a las 3.24.41 PM.png$

El mapa f: P → Q dado por f (a) = v, f (b) = w, f (c) = x, f (d) = y, y f ( e) = z tiene una inversa.

De hecho Q y R son el mismo preorden. Uno puede confundirse por el hecho de que hay una flecha x → z en el diagrama de Hasse para R y no una en Q, pero de hecho esta flecha es superflua. Por la propiedad de transitividad de los preordenes (Definición 1.30), ya que x ≤ y e y ≤ z, debemos tener x ≤ z, ya sea dibujado o no. Del mismo modo, podríamos haber dibujado una flecha v → y en Q o R y no habría cambiado el preorden.

Recordemos el preorden$\mathbb{B}$ = {false, true}, donde false ≤ true. Por sencillo que sea esta preorden, también es una de las más importantes.

Ejercicio 1.77.

Mostrar que el mapa Φ de la Sección 1.1.1, que fue dado aproximadamente por '¿Está • conectado a ∗?' es un mapa monótona Prt ({∗, •, ◦}) → B; véase también la Ec. (1.5) . ♦

Proposición 1.78.

Que P sea un preorden. Los mapas monótonos P →$\mathbb{B}$ están en correspondencia uno a uno con conjuntos superiores de P.

Prueba. Que f: P → B sea un mapa monótona. Mostraremos que el subconjunto f$^{-1}$ (true)$\subseteq$ P es un conjunto superior. Supongamos p$\in$ f$^{-1}$ (true) y p ≤ q; entonces true = f (p) ≤ f (q). Pero en B, si true ≤ f (q) entonces true = f (q). Esto implica q$\in$ f$^{-1}$ (true) y así muestra que f$^{-1}$ (true) es un conjunto superior. Por el contrario, si U es un conjunto superior en P, defina f U: P → B tal que f U (p) = verdadero cuando p$\in$ U, y f U (p) = falso cuando p.$\not in$ U.

Este es un mapa monótono, porque si p ≤ q, entonces ya sea p$\in$ U, entonces q$\in$ U y f (p) = true = f (q), o p$\not in$ U, entonces f (p) = falso ≤ f (q).

Estas dos construcciones son mutuamente inversas, y por lo tanto prueban la proposición.

Ejercicio 1.79 (Mapa Pullback).

Que P y Q sean pedidos por adelantado, y f: P → Q sea un mapa monótono. Entonces podemos definir un mapa monótono f$^{*}$: U (Q) → U (P) enviando una U$\subseteq$ Q al conjunto superior f$^{-1}$ (U)$\subseteq$ P. A esto lo llamamos el retroceso a lo largo de f. Viendo conjuntos superiores como mapas monótonos$\mathbb{B}$ como en la Proposición 1.78, el retroceso puede entenderse en términos de composición. En efecto, mostrar que la f$^{*}$ se define tomando u: Q →$\mathbb{B}$ a (f; u): P → B. ♦