1.2: Cumple y se une

Última actualización
Guardar como PDF

Page ID: 112198

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Como hemos dicho, un preorden es un conjunto P dotado de un orden ≤ que relaciona los elementos. Con respecto a este orden, ciertos elementos de P pueden tener caracterizaciones distintivas, ya sea absolutamente o en relación con otros elementos. Ya hemos discutido uniones antes, pero las discutimos nuevamente ahora que hemos construido algo de formalismo.

Definición y Ejemplos Básicos

Considera el preorden ($\mathbb{R}$, ≤) de números reales ordenados de la manera habitual. El subconjunto$\mathbb{N}$$\subseteq$$\mathbb{R}$ tiene muchos límites inferiores, a saber, −1.5 es un límite inferior: cada elemento de N es mayor que −1.5. Pero dentro de todos los límites inferiores para$\mathbb{N}$$\subseteq$$\mathbb{R}$, uno es distintivo: un mayor límite inferior también llamado encuentro a saber 0. Es un límite inferior, y no hay límite inferior para$\mathbb{N}$ que esté por encima de él. Sin embargo, el conjunto no$\mathbb{N}$$\subseteq$$\mathbb{R}$ tiene límite superior, y ciertamente no menos límite superior que se llamaría unión. Por otro lado, el conjunto

$\left\{\frac{1}{n+1} \mid n \in \mathbb{N}\right\} \subseteq \mathbb{R}$

tiene tanto un límite inferior mayor (encuentro), es decir 0, y un límite inferior inferior (unión), a saber, 1. Estas nociones tendrán correlatos en la teoría de categorías, llamados límites y corlímites, que discutiremos en el Capítulo 3. De manera más general, decimos que estas caracterizaciones distintivas son propiedades universales, ya que, por ejemplo, un mayor límite inferior es el mayor entre todos los límites inferiores. Por ahora, sin embargo, simplemente queremos hacer precisa la definición de mayores límites inferiores y menos límites superiores, llamados meets y joins.

Ejercicio 1.80.

¿Por qué 0 es un límite inferior para$\left\{\frac{1}{n+1} \mid n \in \mathbb{N}\right\} \subseteq \mathbb{R}$
¿Por qué 0 es un límite inferior mayor (meet)? ♦

Definición: 1.81.

Sea (P, ≤) un preorden y que A$\subseteq$ P sea un subconjunto. Decimos que un elemento p$\in$ P es un encuentro de A si

para todos a$\in$ A, tenemos p ≤ a, y
para todos q tal que q ≤ a para todos$\in$ a A, tenemos que q ≤ p.

Escribimos p =$\bigwedge$ A, p =$\bigwedge_{a \in A}$ a, o, si la variable ficticia a es clara del contexto, solo p =$\bigwedge_{A}$ a.

Si A solo consta de dos elementos, digamos A = {a, b}, podemos denotar$\bigwedge$ A simplemente por a$\land$ b.

De igual manera, decimos que p es una unión de A si

para todos a$\in$ A tenemos un ≤ p, y
para todos q tal que a ≤ q para todos$\in$ a A, tenemos que p ≤ q.

Escribimos p =$\begin{equation}V A\end{equation}$ o p =$V_{a \in A} a$ a, o cuando A = {a, b} podemos simplemente escribir p = a$\lor$ b.

Observación 1.82. En la Definición 1.81, cometimos un abuso aparentemente atroz de la notación. Veremos a continuación en el Ejemplo 1.84 que podría haber dos encuentros diferentes de A$\subseteq$ P, digamos p =$\bigwedge A$ y q =$\bigwedge$ A con p$\neq$ q, lo cual no tiene sentido si p$\neq$ q!

Pero de hecho, como usamos el símbolo$\bigwedge$ A, este abuso no importará porque dos encuentros cualesquiera p, q son automáticamente isomórficos: la definición misma de fuerzas de encuentro tanto p ≤ q como q ≤ p, y así tenemos p$\cong$ q. Así que para cualquier x$\in$ P, tenemos p ≤ x iff q ≤ x y x ≤ p iff x ≤ q. Así, siempre y cuando tengamos solo están interesados en elementos de P basados en sus relaciones con otros elementos (y en la teoría de categorías, este es el caso: solo debemos preocuparnos por las cosas en función de cómo interactúan con otras cosas, más que en algún tipo de “esencia interna”), la distinción entre p y q nunca importará.

Esto presagia un tema importante, así como el abuso estándar de la notación en la teoría de categorías, donde dos cosas cualesquiera definidas por la misma propiedad universal son automáticamente equivalentes de una manera conocida como 'único hasta isomorfismo único'; esto significa que generalmente no nos encontramos con problemas si pretendemos que son igual. Recogeremos de nuevo este tema de 'la' vs 'a' en Observación 3.85.

Ejemplo 1.83 (Es posible que no existan las combinaciones o las combinaciones).

Tenga en cuenta que, en un preorden arbitrario (P, ≤), un subconjunto A no necesita tener una reunión o una unión. Considere el conjunto de tres elementos P = {p, q, r} con el orden discreto. El conjunto A = {p, q} no tiene una unión en P porque si x fuera una unión, necesitaríamos p ≤ x y q ≤ x, y no existe tal elemento x.

Ejemplo 1.84 (Pueden existir múltiples conjuntos o combinaciones).

También puede darse el caso de que un subconjunto A tenga más de una reunión o unión. Aquí hay un ejemplo.

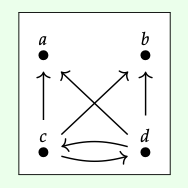
$Screen Shot 2021-01-07 at 6.35.42 PM.png$

Sea A el subconjunto {a, b} en el preorden especificado por este diagrama de Hasse. Entonces tanto c como d son encuentros de A: cualquier elemento menor que tanto a como b es también menor que c, y también menor que d. Obsérvese que, como en Observación 1.82, c ≤ d y d ≤ c, entonces c$\cong$ d. Tal será siempre el caso cuando haya más de un encuentro: cualesquiera dos encuentros del mismo subconjunto serán isomórficos.

Ejercicio 1.85.

Sea (P, ≤) un preorden y p$\in$ P un elemento. Considera el conjunto A = {p} con un elemento.

Demostrar que$\bigwedge$ A$\cong$ p.
Mostrar que si P es de hecho un orden parcial, entonces$\bigwedge$ A = p.
¿Son ciertos los hechos análogos cuando$\bigwedge$ se sustituye por$V$?

Ejemplo 1.86.

En cualquier orden parcial P, tenemos p$\lor$ p = p$\land$ p = p.La razón es que nuestra notación dice p$\lor$ p significa$V$ {p, p}. Pero {p, p} = {p} (ver Sección 1.2.1), entonces p$\lor$ p = p por Ejercicio 1.85.

Ejemplo 1.87.

En un conjunto de potencia P (X), el encuentro de una colección de subconjuntos, digamos A, B$\subseteq$ X es su intersección A$\land$ B = A$\cap$ B, mientras que la unión es su unión, A$\lor$ B = A$\cup$ B.

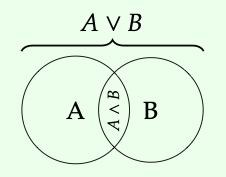
$Screen Shot 2021-01-07 at 6.45.05 PM.png$

Quizás esto justifica la terminología: la unión de dos conjuntos es su unión, el encuentro de dos conjuntos es su intersección.

Ejemplo 1.88.

En los booleanos$\mathbb{B}$ = {false, true} (Ejemplo 1.34), el encuentro de dos elementos cualesquiera viene dado por AND y la unión de cualesquiera dos elementos viene dada por OR (recordar Ejercicio 1.7).

Ejemplo 1.89.

En un orden total, el encuentro de un conjunto es su infimum, mientras que la unión de un conjunto es su supremo. Tenga en cuenta que$\mathbb{B}$ es un orden total, y esto generaliza Ejemplo 1.88.

Ejercicio 1.90.

Recordemos la división ordenando en N del Ejemplo 1.45: escribimos n | m si n se divide perfectamente en m. El encuentro de dos números cualesquiera en esta preorden tiene un nombre común, que quizás hayas aprendido cuando tenías alrededor de los 10 años; ¿qué es? De igual manera la unión de dos números cualesquiera tiene un nombre común; ¿qué es? ♦

Proposición 1.91.

Supongamos que (P, ≤) es un preorden y A$\subseteq$ B$\subseteq$ P son subconjuntos que tienen cumple. Entonces$\bigwedge$ B ≤$\bigwedge$ A. Del mismo modo, si A y B tienen uniones, entonces$V$ A ≤$V$ B.

Prueba. Sea m =$\bigwedge$ A y n =$\bigwedge$ B. Entonces para cualquier a A también tenemos$\in$ un$\in$ B, entonces n ≤ a porque n es un límite inferior para B. Así, n es también un límite inferior para A y por lo tanto n ≤ m, porque m es el límite inferior más grande de A. El segundo reclamo se prueba de manera similar. ♦

Volver a observaciones y efectos generativos

En la tesis [Ada17], Adán piensa en los mapas monótonos como observaciones. Un mapa monótono Φ: P → Q es un fenómeno (podríamos decir “característica”) de P como lo observa Q. Define el efecto generativo de dicho mapa Φ como su incapacidad para preservar uniones (o más generalmente, para categorías, su incapacidad para preservar los corlímites).

Definición: 1.92.

Decimos que un mapa monótono f: P → Q conserva cumple si f (a$\land$ b)$\cong$ f (a)$\land$ f (b) para todos a, b $\in$P. De manera similar decimos f conserva uniones si f (a$\lor$ b)$\cong$ f (a)$\lor$ f (b) para todos a, b$\in$ P.

Definición: 1.93.

Decimos que un mapa monótono f: P → Q tiene un efecto generativo si existen elementos a, b$\in$ P tal que

f (a)$\lor$ f (b)$\cong$ f (a$\lor$ b).

En la Definición 1.93, si pensamos en Φ como una observación o medición de los sistemas a y b, entonces el lado izquierdo f (a)$\lor$ f (b) puede interpretarse como la combinación de la observación de a con la observación de b. Por otra parte, el lado derecho f (a$\lor$ b) es la observación de la sistema combinado a$\lor$ b. La desigualdad implica que vemos algo cuando observamos el sistema combinado que no podíamos esperar simplemente combinando nuestras observaciones de las piezas. Es decir, que hay efectos generativos a partir de la interconexión de los dos sistemas.

Ejercicio 1.94.

En la Definición 1.93, definimos la generatividad de f como la desigualdad f (a$\lor$ b)$\neq$ f (a)$\lor$ f (b), pero en el texto posterior parecíamos implicar que no habría sólo una diferencia, sino más cosas en f (a$\lor$ b) que en f (a)$\lor$ f (b). Demostrar que para cualquier mapa monótono f: P → Q, si a, b$\in$ P tienen una unión y f (a), f (b)$\in$ Q tienen una unión, entonces efectivamente f (a)$\lor$ f (b) ≤ f (a$\lor$ b) . ♦

En su trabajo sobre los efectos generativos, Adán restringe su atención a los mapas generativos que preservan los encuentros (pero no preservan las uniones). La preservación de los encuentros implica que el mapa Φ se comporta bien cuando se restringe a subsistemas, aunque puede arrojar sorpresas al unir sistemas.

Esta discusión conduce naturalmente a las conexiones de Galois, que son pares de mapas monótonos entre preordenes, uno de los cuales conserva todas las uniones y el otro de los cuales conserva todos los encuentros.