2.1: Pasando de a a b

No se puede hacer una tortilla sin romper un huevo. Para obtener las cosas que queremos se requieren recursos, y el proceso de transformar lo que tenemos en lo que queremos suele ser intrincado. En este capítulo, discutiremos cómo los prepedidos monoidales pueden ayudarnos a pensar en este asunto.

Considera las siguientes tres preguntas que podrías hacerte:

• Dado lo que tengo, ¿es posible conseguir lo que quiero?
• Dado lo que tengo, ¿cuál es el costo mínimo para conseguir lo que quiero?
• Dado lo que tengo, ¿cuál es el conjunto de formas de conseguir lo que quiero?

Estas preguntas son sobre los recursos que tienes y los que quieres pero quizás lo más importante, se trata de pasar de tener que querer: posibilidad de, costo de, y formas de.

Tales preguntas surgen no sólo en nuestras vidas, sino también en la ciencia y la industria. En química, uno pregunta si un cierto conjunto de compuestos se puede transformar en otro conjunto, cuánta energía requerirá tal reacción, o qué métodos existen para hacerla realidad. En manufactura, uno hace preguntas similares.

Desde un punto de vista externo, tanto un químico como una empresa industrial pueden ser considerados como depósitos de información sobre los temas anteriores. El químico sabe qué compuestos puede hacer dados otros, y cómo hacerlo; la firma ha almacenado conocimientos del mismo tipo. El trabajo de investigación del químico y de la firma es utilizar lo que saben para derivar o descubrir nuevos conocimientos.

Este es más o menos el primer objetivo de este capítulo: discutir un formalismo para expresar recetas métodos para transformar un conjunto de recursos en otro y para derivar nuevas recetas de lo antiguo. La idea aquí no es complicada, ni en la vida ni en nuestro formalismo matemático. El valor agregado entonces es simplemente ver cómo funciona, para que podamos construir sobre él dentro del libro, y así otros puedan construir sobre él en su propio trabajo.

Discutimos brevemente el enfoque categórico de esta idea, es decir, el de los prepedidos monoidales para construir nuevas recetas antiguas. El siguiente diagrama de cableado muestra, asumiendo que se sabe cómo implementar cada una de las cajas interiores, cómo implementar la preparación de un pastel de merengue de limón:

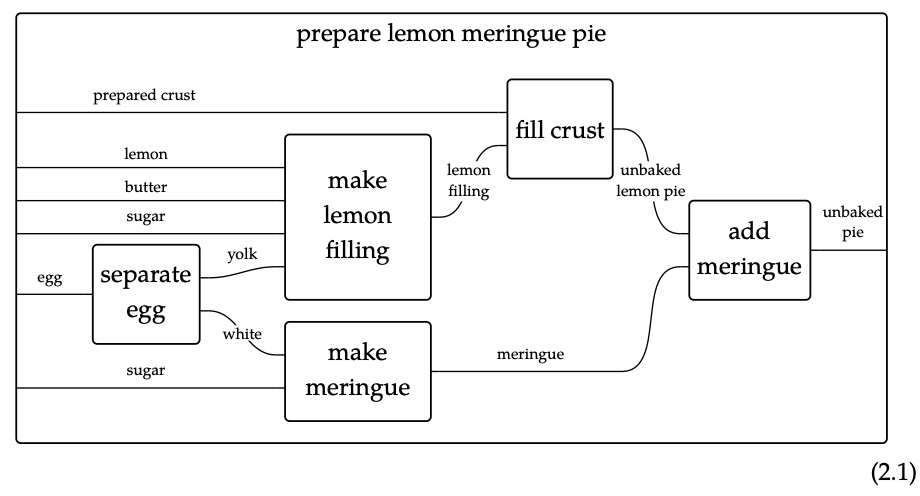
Los cables muestran recursos: comenzamos con corteza preparada, limón, mantequilla, azúcar y recursos de huevo, y terminamos con un recurso de pastel sin hornear. Podríamos tomar todo este método y combinarlo con otros, por ejemplo, hornear el pastel:

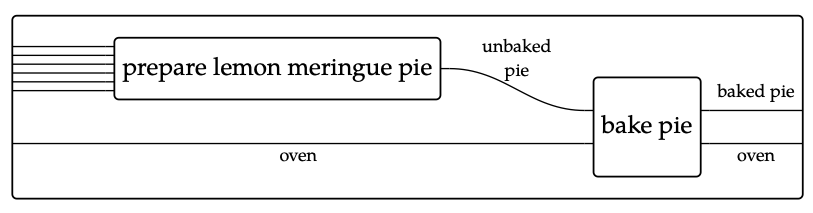
En el ejemplo anterior vemos que los recursos no siempre se consumen cuando se utilizan. Por ejemplo, usamos un horno para convertir o catalizar la transformación de un pastel sin hornear en un pastel horneado, y recuperamos el horno una vez que terminamos. ¡Es una buena característica de los hornos! Para usar términos económicos, el horno es un “medio de producción” para tartas.

Los diagramas de cadena son objetos matemáticos importantes que surgirán repetidamente en este libro. Fueron inventados en el contexto matemático más específicamente en el contexto de categorías monoidales por Joyal y Street [JS93], pero han sido utilizados de manera menos formal por ingenieros y científicos en diversos contextos durante mucho tiempo.

Como dijimos anteriormente, nuestro primer objetivo en este capítulo es utilizar preordenes monoidales, y los diagramas de cableado correspondientes, como lenguaje formal para recetas antiguas. Nuestro segundo objetivo es discutir algo llamado categorías V para diversos preordenes monoidales V.

Una categoría V es un conjunto de objetos, que uno puede pensar como puntos en un mapa, donde V de alguna manera “estructura la cuestión” de llegar del punto a al punto b. Los ejemplos de preordenes monoidales V que más nos interesarán se llaman Bool y Cost. En términos generales, una categoría Bool es un conjunto de puntos donde la cuestión de llegar del punto a al punto b tiene una respuesta verdadera/falsa. A Costo-categoría es un conjunto de puntos donde la cuestión de pasar de a a b tiene una respuesta d\(\in\) [0, ∞], un costo.

Esta historia funciona en más generalidad que los preordenes monoidales. En efecto, en el Capítulo 4 discutiremos algo llamado categoría monoidal, noción que generaliza los preordenes monoidales, y generalizaremos la definición de categoría V en consecuencia. En esta configuración más general, las categorías V también pueden abordar nuestra tercera pregunta anterior, describiendo métodos para meterse entre puntos. Por ejemplo, una categoría Set es un conjunto de puntos donde la cuestión de llegar del punto a al punto b tiene un conjunto de respuestas (elementos de los cuales podrían llamarse métodos).

Comenzaremos en la Sección 2.2 definiendo preordenes monoidales simétricos, dando algunos ejemplos preliminares y discutiendo diagramas de cableado. Luego damos muchos más ejemplos de preordenes monoidales simétricos, incluyendo tanto algunos ejemplos del mundo real, en forma de teorías de recursos, como algunos ejemplos matemáticos que volverán a aparecer a lo largo del libro. En la Sección 2.3 discutimos el enriquecimiento y las categorías V cómo un preorden monoidal V puede “estructurar la cuestión” de pasar de a a b y luego dar algunas construcciones importantes sobre las categorías V (Sección 2.4), y analizarlas usando una especie de técnica de multiplicación matricial (Sección 2.5).