2.2: Preordenes monoidales simétricos

Última actualización
Guardar como PDF

Page ID: 112308

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la Sección 1.2.2 introdujimos los pedidos anticipados. La notación para un preorden, es decir (X, ≤), se refiere a dos piezas de estructura: un conjunto llamado X y una relación llamada ≤ que es reflexiva y transitiva. Queremos agregar al concepto de preordenes una forma de combinar elementos en X, una operación tomando dos elementos y sumando o multiplicándolos juntos. Sin embargo, la operación no tiene que ser literalmente suma o multiplicación; solo necesita satisfacer algunas de las propiedades que uno espera de ellas.

Definición y primeros ejemplos

Comenzamos con una definición formal de preordenes monoidales simétricos.

Definición 2.2: Estructura monoidal simétrica

Una estructura monoidal simétrica en un preorden (X, ≤) consta de dos componentes:

un elemento I$\in$ X, llamado unidad monoidal, y
a función: X × X → X, llamada el producto monoidal.

Estos constituyentes deben satisfacer las siguientes propiedades, donde escribimos ($x_{1}$,$x_{2}$)$x_{1}$ =$x_{2}$:

para todos$x_{1}$,$x_{2}$$y_{1}$,,$y_{2}$$\in$ X, si$x_{1}$$x_{2}$ ≤$y_{1}$ y ≤$y_{2}$$x_{1}$, entonces$x_{2}$$y_{1}$ ≤$y_{2}$,
para todos x$\in$ X, las ecuaciones I x = x y x I = x hold,
para todos x, y, z$\in$ X, se mantiene la ecuación (x y) z = x (y z), y
para todos x, y$\in$ X, se mantiene la ecuación x y = y x.

A estas condiciones las llamamos monotonicidad, unidad, asociatividad y simetría respectivamente.

Un preorden equipado con una estructura monoidal simétrica, (X, ≤, I,), se denomina preorden monoidal simétrico.

Cualquiera puede proponer un conjunto X, un orden ≤ en X, un elemento I en X y una operación binaria en X y preguntar si (X, ≤, I,) es un preorden monoidal simétrico. Y efectivamente será uno, siempre y cuando satisfaga las reglas a, b, c y d de la Definición 2.2.

OBSERVACIÓN 2.3. A menudo es útil reemplazar = con a$\cong$ lo largo de la Definición 2.2. El resultado es una noción perfectamente buena, llamada estructura monoidal débil. La razón por la que elegimos la igualdad es que hace que las ecuaciones parezcan más simples, lo que esperamos ayude a los lectores primerizos

La notación para la unidad monoidal y el producto monoidal puede variar: las unidades monoidales que hemos visto incluyen I (como en la definición), 0, 1, true, false, {∗}, y más. Los productos monoidales que hemos visto incluyen (como en la definición), +, ∗$\land$,$\lor$, y ×. La notación preferida en un entorno dado es lo que mejor ayuda a nuestros cerebros a recordar lo que estamos tratando de hacer; los nombres I y son solo valores predeterminados.

Ejemplo 2.4.

Existe una estructura de preorden bien conocida, denotada ≤, en el conjunto$\mathbb{R}$ de números reales; e.g$\leq$$\sqrt{2}$. -5.

Proponemos 0 como unidad monoidal y +:$\mathbb{R}$ ×$\mathbb{R}$ →$\mathbb{R}$ como producto monoidal. ¿($\mathbb{R}$, ≤, 0, +) satisface las condiciones de la Definición 2.2?

Si$x_{1}$ ≤$y_{1}$ y$x_{2}$ ≤$y_{2}$, es cierto que$x_{1}$ +$x_{2}$ ≤$y_{1}$ +$y_{2}$.

También es cierto que 0 + x = x y x + 0 x, que (x + y) + z = x + (y + z), y que x + y = y + x. Así ($\mathbb{R}$, ≤, 0, +) satisface las condiciones de ser un preorden monoidal simétrico.

Ejercicio 2.5.

Consideremos nuevamente el preorden ($\mathbb{R}$, ≤) del Ejemplo 2.4. Alguien propone 1 como unidad monoidal y ∗ (multiplicación habitual) como producto monoidal. Pero un experto pasa y dice “eso no va a funcionar”. ¡Descubre por qué, o prueba que el experto se equivoca!

Ejemplo 2.6

Un monoide consiste en un conjunto M, una función ∗: M × M → M llamada la multiplicación monoide, y un elemento e$\in$ M llamado la unidad monoide, tal que, cuando escribes ∗ (m , n) como m ∗ n, es decir, usando notación infija, las ecuaciones

m ∗ e = m, e ∗ m = m, (m ∗ n) ∗ p = m ∗ (n ∗ p) (2.7)

mantener para todos m, n, p ∈ M. Se llama conmutativa si también m ∗ n = n ∗ m.
Cada conjunto S determina un preorden discreto$Disc_{S} $ (donde m ≤ n iff m = n; ver Ejemplo 1.32), y es fácil verificar que si (M, e, ∗) es un monoide conmutativo entonces ($Disc_{M}$, =, e, ∗) es un preorden monoidal simétrico.

Ejercicio 2.8.

Dijimos que era fácil comprobar que si (M, ∗, e) es un monoide conmutativo entonces ($Disc_{M}$, =, ∗, e) es un preorden monoidal simétrico. ¿Estamos diciendo la verdad? ♦

Ejemplo 2.9.

Aquí hay un no-ejemplo para las personas que conocen el juego “poker estándar”. Que H sea el conjunto de todas las manos de póquer, donde una mano significa una opción de cinco cartas de la baraja estándar de 52 cartas. Como orden, poner h ≤ h ′ si h ′ late o es igual a h en el poker.

Se podría proponer un producto monoidal: H × H → H asignando$h_{2}$ para$h_{1}$ que sea “la mejor mano que uno pueda formar de las diez cartas en$h_{1}$ y”$h_{2}$. Si algunas cartas están en ambas$h_{1}$ y$h_{2}$, simplemente tira los duplicados. Entonces por ejemplo {2 ♥, 3 ♥, 4 ♥, 6 ♠, 7 ♠} {2 ♥, 5 ♥, 6 ♥, 6 ♠, 7 ♠} = {2 ♥, 3 ♥, 4 ♥, 5 ♥, 6 ♥}, porque esta última es la mejor mano que puedes hacer con las dos primeras.

Esta propuesta de una estructura monoidal fallará la condición (a) de la Definición 2.2: podría darse el caso de que$h_{1}$ ≤$i_{1}$ y$h_{2}$ ≤$i_{2}$, y sin embargo no ser el caso$h_{1}$ de que $h_{2}$$i_{1}$≤$i_{2}$. Por ejemplo, considere este caso:

$h_{1}$:= {2 ♥, 3 ♥, 10 ♠, J ♠, Q ♠}$i_{1}$ := {4 ♣, 4 ♠, 6 ♥, 6 ♦, 10 ♦}

$h_{2}$:= {2 ♦, 3 ♦, 4 ♦, K ♠, A ♠}$h_{2}$ := {5 ♠, 5 ♥, 7 ♥, J ♦, Q ♦}.

Aquí,$h_{1}$ ≤$i_{1}$ y$h_{2}$ ≤$i_{2}$, pero$h_{1}$$h_{2}$ = {10 ♠, J ♠, Q ♠, K ♠, A ♠} es la mejor mano posible y late$i_{1}$$i_{2}$ = {5 ♠, 5 ♥, 6 ♥, 6 ♦, Q ♦}.

Las subsecciones 2.2.3 y 2.2.4 están dedicadas a ejemplos de preordenes monoidales simétricos. Algunos están alineados con la noción de teorías de recursos, otros provienen de la matemática pura. Al hablar de lo primero, usaremos diagramas de cableado, así que aquí hay una imprimación rápida.

Presentamos diagramas de cableado

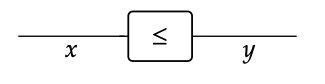
Los diagramas de cableado son representaciones visuales para construir nuevas relaciones desde la antigüedad. En un preorden sin una estructura monoidal, el único tipo de relación entre los objetos es ≤, y la única manera de construir una nueva ≤ relación a partir de los antiguos es encadenándolos juntos. Denotamos la relación x ≤ y por

$Screen Shot 2021-01-05 a las 5.33.05 PM.png$

Podemos encadenar algún número de estas ≤ relaciones digamos 0, 1, 2 o 3 de ellas juntas en serie como se muestra aquí

$Screen Shot 2021-01-05 a las 5.34.00 PM.png$

Si agregamos una estructura monoidal simétrica, podemos combinar relaciones no sólo en serie sino también en paralelo. Aquí hay un ejemplo:

$Screen Shot 2021-01-05 a las 5.34.37 PM.png$

Diferentes estilos de diagramas de cableado De hecho, veremos más adelante que hay muchos estilos de diagramas de cableado. Cuando se trata de pedidos anticipados, el tipo de diagrama de cableado que podemos dibujar es que con cajas de entrada única y salida única conectadas en serie. Cuando se trata de preordenes monoidales simétricos, podemos tener cajas más complejas y diagramas de cableado más complejos, incluida la composición paralela. Posteriormente veremos que para otro tipo de estructuras categóricas, hay otros estilos de diagramas de cableado:

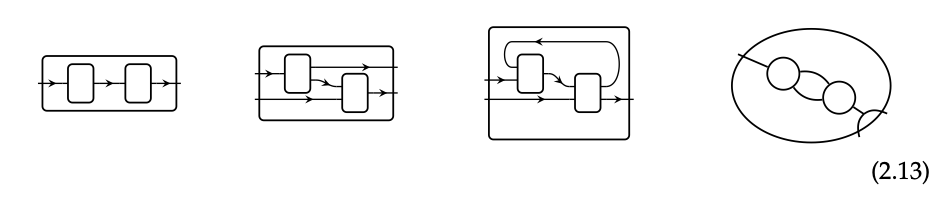
$Screen Shot 2021-01-05 a las 5.36.00 PM.png$

Diagramas de cableado para preordenes monoidales simétricos El estilo de diagrama de cableado que tiene sentido en cualquier preorden monoidal simétrico es el que se muestra en la Ec. (2.12): las cajas pueden tener múltiples entradas y salidas, y pueden estar dispuestas en serie y en paralelo. Los preordenes monoidales simétricos y sus diagramas de cableado están estrechamente acoplados entre sí. ¿Cómo es así?

La respuesta es que un preorden monoidal (X, ≤, I,) tiene alguna noción de elemento (x$\in$ X), relación (≤) y combinación (usando transitividad y), y también lo hacen los diagramas de cableado: los cables representan elementos, las cajas representan relaciones, y los propios diagramas de cableado muestran cómo se pueden combinar las relaciones. Llamamos iconos de cajas y cables; encontraremos varios íconos más en este capítulo, y a lo largo del libro.

Para ser un poco más rigurosos sobre la conexión, comencemos con un preorden monoidal (X, ≤, I,) como en la Definición 2.2. Los diagramas de cableado tienen cables a la izquierda y a la derecha. Cada elemento x$\in$ X se puede hacer la etiqueta de un alambre. Tenga en cuenta que dados dos objetos x, y, podemos dibujar dos cables en paralelo uno etiquetado x y otro etiquetado y o podemos dibujar un cable etiquetado x y.

$Screen Shot 2021-01-05 a las 5.36.36 PM.png$

Consideramos alambres en paralelo para representar el producto monoidal de sus etiquetas, por lo que consideramos ambos casos anteriores para representar el elemento x y. Tenga en cuenta también que un cable etiquetado I o una ausencia de cables:

$Screen Shot 2021-01-05 a las 5.37.21 PM.png$

ambos representan la unidad monoidal I; otra forma de pensar de esto es que la unidad es el producto monoidal vacío.

Un diagrama de cableado se extiende entre un conjunto de cables paralelos a la izquierda y un conjunto de cables paralelos a la derecha. Decimos que un diagrama de cableado es válido si el producto monoidal de los elementos de la izquierda es menor que el producto monoidal de los de la derecha. Por ejemplo, si tenemos la desigualdad x ≤ y, el diagrama que es una caja con un cable etiquetado x a la izquierda y un cable etiquetado y a la derecha es válido; vea el primer cuadro a continuación:

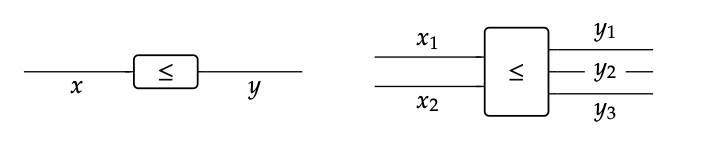
$Screen Shot 2021-01-05 a las 5.38.11 PM.png$

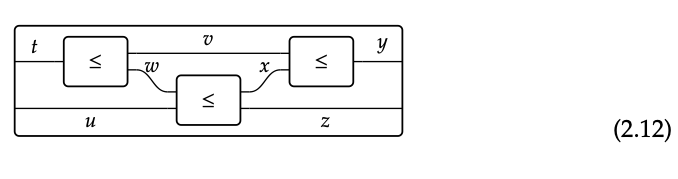
La validez de la segunda caja corresponde a$x_{1}$ la$y_{1}$ desigualdad$x_{2}$$y_{2}$ ≤$y_{3}$. Antes de pasar a las propiedades de la Definición 2.2, hagamos una pausa para ver un ejemplo de lo que hemos discutido hasta ahora.

Ejemplo 2.14.

Recordemos el preorden monoidal simétrico ($\mathbb{R}$, ≤, 0, +) del Ejemplo 2.4. Los diagramas de cableado para ello permiten cables etiquetados por números reales. Dibujar cables en paralelo corresponde a agregar sus etiquetas, y el cable etiquetado como 0 equivale a no tener cables en absoluto.

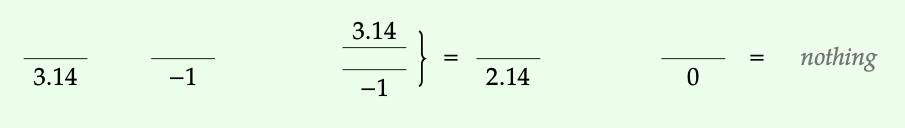
$Screen Shot 2021-01-10 a las 12.57.09 PM.png$

Y aquí expresamos un par de datos sobre ($\mathbb{R}$, ≤, 0, +) en este idioma: 4 ≤ 7 y 2+5 ≤ −1+5+3.

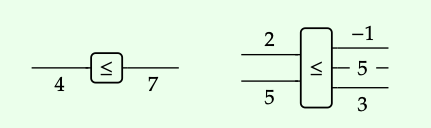
$Screen Shot 2021-01-10 en 1.27.03 PM.png$

Ahora volvemos a cómo las propiedades de los preordenes monoidales simétricos corresponden a propiedades de este tipo de diagrama de cableado. Hablemos primero de la estructura del orden: condiciones (a) reflexividad y (b) transitividad a partir de la Definición 1.30. Reflexivity dice que x ≤ x, esto significa que el diagrama solo consiste en un cable

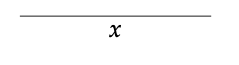
$Screen Shot 2021-01-05 a las 5.39.27 PM.png$

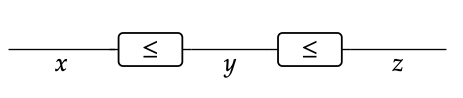
siempre es válido. La transitividad nos permite conectar hechos juntos: dice que si x ≤ y e y ≤ z, entonces x ≤ z. Esto significa que si los diagramas

$Screen Shot 2021-01-05 a las 5.40.07 PM.png$

son válidos, podemos juntarlos y obtener el diagrama válido

$Screen Shot 2021-01-05 a las 5.41.43 PM.png$

A continuación hablemos de las propiedades (a) — (d) a partir de la definición de estructura monoidal simétrica (Definición 2.2). La propiedad (a) dice que si$x_{1}$$x_{2}$ ≤$y_{1}$ y$x_{1}$ ≤$y_{2}$ entonces$x_{2}$$y_{1}$ ≤$y_{2}$. Esto corresponde a la idea de que apilar dos cajas válidas cualesquiera en paralelo sigue siendo válido:

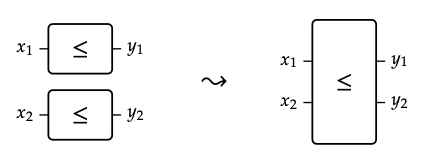
$Screen Shot 2021-01-05 a las 5.42.23 PM.png$

Condición (b), que I x = x y x I = x, dice que no necesitamos preocuparnos por I o espacio en blanco; en particular los diagramas como los siguientes son válidos:

$Screen Shot 2021-01-05 a las 5.42.55 PM.png$

Condición (c), que (x y) z = x (y z) dice que no tenemos que preocuparnos por si construimos diagramas desde arriba o desde abajo

$Screen Shot 2021-01-05 a las 5.43.33 PM.png$

Pero esto parece mucho más difícil de lo que es: la propiedad asociativa debe pensarse como diciendo que no hay distinción entre las cosas de arriba a la izquierda y las cosas de la derecha, i.e.

$Screen Shot 2021-01-05 a las 5.44.11 PM.png$

y de hecho es válido un diagrama que se mueve de uno a otro.
Finalmente, la condición de simetría (d), que x y = y x, dice que un diagrama es válido aunque sus cables crucen:

$Screen Shot 2021-01-05 a las 5.44.51 PM.png$

Se puede considerar el par de cables cruzados como otro icono en nuestra iconografía, además de las cajas y cables que ya tenemos.

Diagramas de cableado como pruebas gráficas Dado un preorden monoidal X = (X, ≤, I,), un diagrama de cableado es una prueba gráfica de algo sobre X. Cada caja del diagrama tiene un lado izquierdo y un lado derecho, digamos x e y, y representa la afirmación de que x ≤ y.

$Screen Shot 2021-01-05 a las 5.45.32 PM.png$

Un diagrama de cableado es un montón de cajas interiores conectadas entre sí dentro de una caja exterior. Representa una prueba gráfica que dice: si todas las aseveraciones interiores son correctas, entonces también lo es la afirmación exterior.

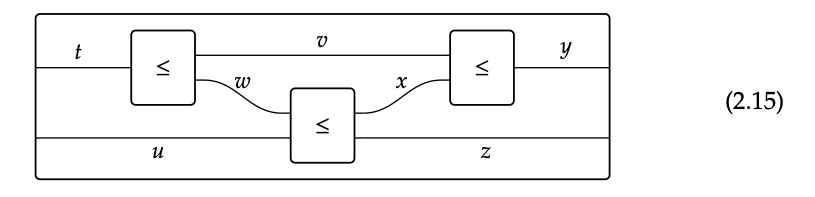
$Screen Shot 2021-01-05 a las 5.46.08 PM.png$

Los recuadros internos en la Ec. (2.15) se traducen en las aseveraciones:

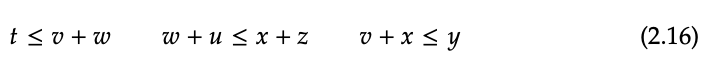
$Screen Shot 2021-01-05 a las 5.46.42 PM.png$

y la caja externa se traduce en la aserción:

$Screen Shot 2021-01-05 a las 5.47.22 PM.png$

Todo el diagrama de cableado 2.15 dice “si sabes que las aseveraciones en 2.16 son ciertas, entonces yo soy una prueba de que la aserción en 2.17 también es cierta”. ¿Cuál es exactamente la prueba que representa el diagrama 2.15? Es la prueba

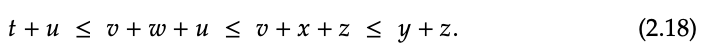
$Screen Shot 2021-01-05 a las 5.48.00 PM.png$

De hecho, cada desigualdad aquí es un corte vertical del diagrama 2.15, y la transitividad de estas desigualdades se expresa conectando estos cortes verticales entre sí.

Ejemplo 2.19.

Recordemos el diagrama de cableado del pastel de merengue de limón de la Ec. (2.1). Tiene cinco cajas interiores, como “huevo separado” y “relleno de corteza”, y tiene una caja exterior llamada “prepare pastel de merengue de limón”. Cada caja es la aseveración de que, dada la recolección de recursos de la izquierda, digamos un huevo, se puede transformar en la recolección de recursos a la derecha, digamos una clara de huevo y una yema de huevo. Todo el diagrama de cuerdas es una prueba de que si cada una de las aseveraciones interiores es cierta es decir, realmente sabes separar los huevos, hacer relleno de limón, hacer merengue, rellenar la corteza y agregar merengue entonces la aseveración exterior es cierta: puedes preparar un pastel de merengue de limón.

Ejercicio 2.20.

La cadena de desigualdades en la ecuación (2.18) no es toda una prueba, porque técnicamente no existe tal cosa como v + w + u, por ejemplo. En cambio, hay (v + w) + u y v + (w + u), y así sucesivamente.

Demostrar formalmente, utilizando únicamente las reglas de los preordenes monoidales simétricos (Definición 2.2), que dadas las aseveraciones en la Ec. (2.16), sigue la conclusión en la Ec. (2.17).
La reflexividad y la transitividad deben aparecer en tu prueba. Asegúrate de ser explícito sobre dónde lo hacen.
¿Cómo se puede observar el diagrama de cableado Eq. (2.12) y saber que no es necesario invocar el axioma de simetría (Definición 2.2 (d))? ♦

A continuación discutimos algunos ejemplos de preordenes monoidales simétricos. Comenzamos en la Sección 2.2.3 con algunos ejemplos más concretos, desde la ciencia, el comercio y la informática. Luego en la Sección 2.2.4 discutimos algunos ejemplos que surgen de la matemática pura, algunos de los cuales obtendrán una buena cantidad de uso más adelante, por ejemplo, en el Capítulo 4.

Ejemplos aplicados

Las teorías de recursos son estudios de cómo se intercambian los recursos en un ámbito determinado. Por ejemplo, en la teoría de los recursos sociales se estudia un mercado donde se pueden comercializar combinaciones de bienes y convertirlas en otras combinaciones de bienes.

Mientras que los mercados son muy dinámicos, y una manzana podría ser negociable por una naranja el domingo pero no el lunes, lo que entendemos por teoría de recursos en este capítulo es una noción estática: decidir “qué compra qué”, de una vez por todas.1 Este tipo de noción estática de conversión podría ocurrir en la química: la química reacciones que son posibles algún día probablemente también serán posibles en otro día. La manufactura puede estar en algún punto intermedio: el conjunto de técnicas de producción, mediante el cual una empresa puede convertir un conjunto de recursos en otro no cambia mucho de un día a otro.

Aprendimos sobre las teorías de recursos de [CFS16; Fri17], quienes van mucho más allá de lo que lo haremos; ver Sección 2.6 para más información. En esta sección nos centraremos únicamente en la idea principal. Si bien hay muchos hermosos ejemplos matemáticos de preordenes monoidales simétricos, como veremos en la Sección 2.2.4, también hay ejemplos ad hoc provenientes de la experiencia de vida. En el siguiente capítulo, sobre bases de datos, veremos el mismo tema: si bien hay algunas categorías matemáticas hermosas por ahí, los esquemas de bases de datos son patrones organizacionales ad hoc de información. Describir algo como “ad hoc” a menudo se considera despectivo, pero solo significa “formado, arreglado o hecho solo para un propósito particular”. No hay nada malo en hacer las cosas con un propósito particular; es común fuera de las matemáticas puras y el arte puro. Vamos a llegar a ello.

Química En la química de secundaria, trabajamos con ecuaciones químicas, donde colecciones mate- rial como

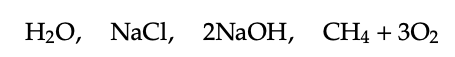
$Screen Shot 2021-01-05 a las 5.50.41 PM.png$

se juntan en forma de ecuaciones de reacción, tales como

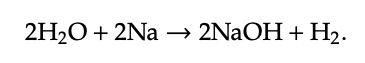
$Screen Shot 2021-01-05 a las 5.51.19 PM.png$

La colección de la izquierda, 2H2O + 2Na se llama el reactivo, y la recolección a la derecha, 2NaOH + H2 se llama el producto.

Podemos considerar ecuaciones de reacción como la anterior como ocurriendo dentro de un solo preorden monoidal simétrico (Mat, →, 0, +). Aquí Mat es el conjunto de todas las colecciones de átomos y moléculas, a veces llamados materiales. Así que tenemos NaCl$\in$ Mat y 4H2O + 6Ne$\in$ Mat.

El conjunto Mat tiene una estructura de preorden denotada por el símbolo →, que es el símbolo preferido en la configuración de la química.

Para ser claros, → está tomando el lugar de la relación de orden ≤ de la Definición 2.2. El símbolo + es la notación preferida para el producto monoidal en el entorno químico, tomando el lugar de. Si bien no surge en la práctica, utilizamos 0 para denotar la unidad monoidal.

Ejercicio 2.21.

Aquí hay un ejercicio para personas familiarizadas con ecuaciones de reacción: verificar que se mantengan las condiciones (a), (b), (c) y (d) de la Definición 2.2.

Una noción importante en química es la de la catálisis: un compuesto cataliza una determinada reacción. Por ejemplo, uno podría tener el siguiente conjunto de reacciones:

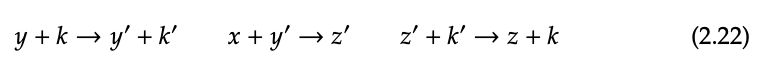
$Screen Shot 2021-01-05 a las 5.51.53 PM.png$

Usando las leyes de los preordenes monoidales, obtenemos la reacción compuesta

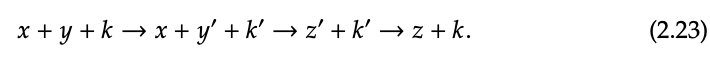
$Screen Shot 2021-01-05 a las 5.52.23 PM.png$

Aquí k es el catalizador porque se encuentra tanto en el reactivo como en el producto de la reacción. Se dice que cataliza la reacción x + y → z.

La idea es que la reacción x + y → z no puede tener lugar dadas las reacciones en la Ec. (2.22). Pero si k está presente, es decir, si agregamos k a ambos lados, la reacción resultante puede tener lugar.

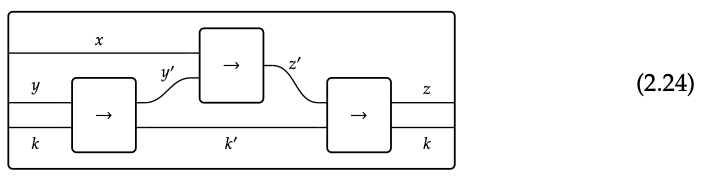
El diagrama de cableado para la reacción en la Ec. (2.23) se muestra en la Ec. (2.24). Las tres cajas interiores corresponden a las tres reacciones dadas en la Ec. (2.22), y la caja exterior corresponde a la reacción compuesta x + y + k → z + k.

$Screen Shot 2021-01-05 at 5.53.44 PM.png$

Fabricando estamos hablando de hornear pasteles, construir teléfonos inteligentes o seguir recetas farmacéuticas, las empresas manufactureras necesitan almacenar recetas básicas, y construir nuevas recetas combinando recetas más simples en esquemas como el que se muestra en la Eq. (2.1) o Eq. (2.24).

La idea básica en la fabricación es exactamente la misma que la de la química, excepto que hay una suposición importante que podemos hacer en la fabricación que no se sostiene para las reacciones químicas:

Puedes tirar basura lo que quieras, y desaparece de la vista.

Esta simple suposición le ha causado al mundo algunos problemas significativos, pero sigue vigente. En nuestro ejemplo de pastel de merengue, podemos preguntar: “¿qué pasó con la cáscara de huevo, o el papel que envuelve la barra de mantequilla”? La respuesta es que fueron destrozados, es decir, tirados al cubo de la basura. Ciertamente desordenaría nuestro diagrama y nuestro pensamiento si tuviéramos que llevar estos recursos a través del diagrama:

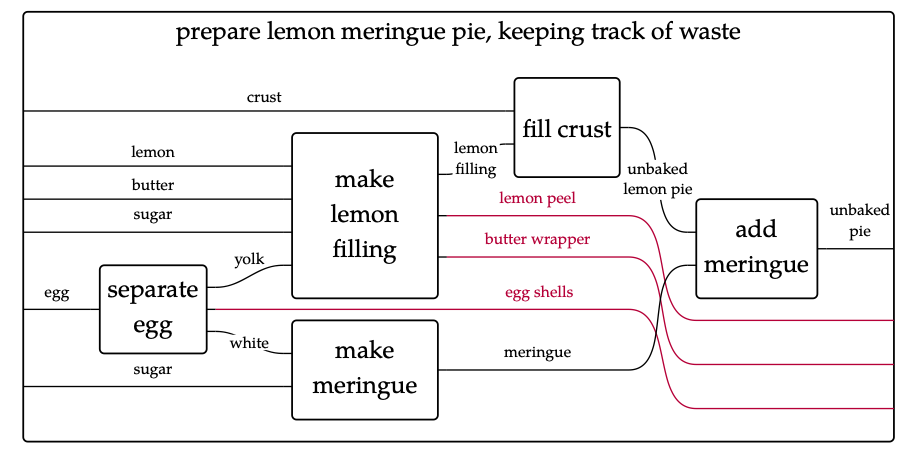
$Screen Shot 2021-01-05 a las 5.55.48 PM.png$

En cambio, en nuestra vida cotidiana y en la manufactura, no tenemos que aferrarnos a algo si no lo necesitamos; podemos simplemente descartarlo. En términos de diagramas de cableado, esto se puede mostrar usando un nuevo icono, de la siguiente manera:

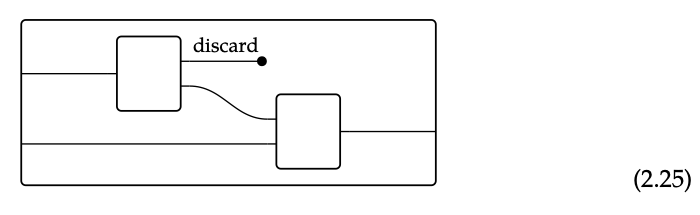
$Screen Shot 2021-01-05 a las 5.56.20 PM.png$

Para modelar este concepto de residuos utilizando categorías monoidales, se añade un axioma adicional a (a), (b), (c) y (d) de la Definición 2.2: (e) x ≤ I para todos $\in$x X. (desechar axioma) Dice que cada x se puede convertir en la unidad monoidal I. En la notación de la sección de química, escribiríamos en su lugar x → 0: cualquier x no da nada. Pero esto ciertamente no es aceptado en el ámbito de la química. Por ejemplo,

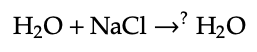
$Screen Shot 2021-01-05 at 5.57.02 PM.png$

ciertamente no es una ecuación química legal. Es fácil tirar las cosas en la fabricación, porque asumimos que tenemos acceso a, la capacidad de agarrar y manipular directamente cada artículo producido. En química, cuando tienes 1023 de sustancia A disuelta en otra cosa, no puedes simplemente descartar A. Por lo que el axioma (e) es válido en la manufactura pero no en la química.

Recordemos que en la Sección 2.2.2 dijimos que había muchos estilos diferentes de diagramas de cableado. Ahora estamos diciendo que sumar el axioma de descarte cambia el estilo del diagrama de cableado, en que agrega este nuevo icono de descarte que permite que los cables terminen, como se muestra en la Ec. (2.25). En informática, volveremos a cambiar el estilo del diagrama de cableado.

Informática Una diferencia importante entre la información y un objeto físico es que la información puede copiarse. Mientras que una taza de mantequilla nunca se convierte en dos, es fácil que se envíe un solo correo electrónico a dos personas diferentes. Es mucho más fácil copiar un archivo de música que copiar un CD. Aquí no nos referimos a “copiar la información de un disco compacto a otro” por supuesto que es fácil en cambio, queremos decir que es bastante difícil copiar el disco físico, ¡formando así un segundo disco físico! En los diagramas, la distinción es entre la relación

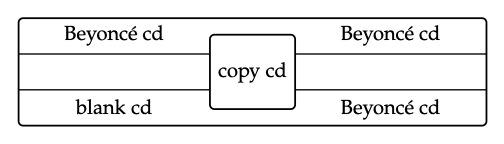
$Screen Shot 2021-01-05 a las 5.57.45 PM.png$

y la relación

$Screen Shot 2021-01-05 a las 5.58.21 PM.png$

El primero es posible, el segundo es mágico.
Por supuesto, a veces se pueden copiar objetos materiales; la mitosis celular es un ejemplo de ello.

Pero este es un proceso biológico notable, desde luego no algo que se espera para los objetos materiales ordinarios. En el mundo físico, haríamos de la mitosis una caja transformando una célula en dos. Pero en la información (clásica, no cuántica), todo se puede copiar, así que agregamos un nuevo icono a nuestro repertorio.

Es decir, en la notación de diagrama de cableado, la información de copia aparece como un nuevo icono$\begin{equation}-x\end{equation}$, lo que nos permite dividir cables:

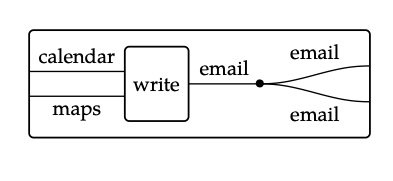
$Screen Shot 2021-01-05 a las 5.59.55 PM.png$

Ahora con dos copias del correo electrónico, podemos enviar una a Alice y otra a Bob.

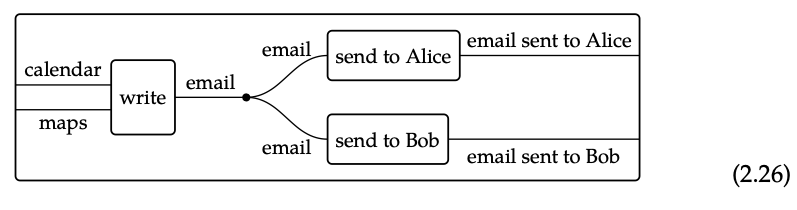
$Screen Shot 2021-01-05 a las 6.00.33 PM.png$

La información también puede descartarse, al menos en la forma convencional de pensar, por lo que además de los axiomas (a) a (d) de la Definición 2.2, podemos mantener el axioma (e) de la página 50 y agregar una nueva copia axioma:

(f) x ≤ x + x para todos $\in$x X. (copia axioma)

lo que nos permite dar sentido matemático a diagramas como la Ec. (2.26). Ahora que tenemos ejemplos de preordenes monoidales en nuestro haber, discutamos algunos buenos ejemplos matemáticos.

Ejemplos abstractos

En esta sección discutimos varios ejemplos matemáticos de estructuras monoidales simétricas en preordenes.

Los booleanos El preorden no trivial más simple son los booleanos:$\mathbb{B}$ = {true, false} con false ≤ true. Hay dos estructuras monoidales simétricas diferentes en él.

Ejemplo 2.27 (Booleanos con Y).

Podemos definir una estructura monoidal sobre$\mathbb{B}$ dejando que la unidad monoidal sea verdadera y el producto monoidal sea$\wedge$ (AND). Si se piensa en false = 0 y true = 1, entonces$\wedge$ corresponde a la operación de multiplicación usual ∗. Es decir, con esta correspondencia, coinciden las dos tablas siguientes:

$Screen Shot 2021-01-10 en 1.50.32 PM.png$

Se puede comprobar que todas las propiedades en Definición 2.2 se mantienen, así que tenemos un preorden monoidal que denotamos Bool: = ($\mathbb{B}$, ≤, true,$\wedge$).

Bool será importante cuando lleguemos a la noción de enriquecimiento. Enriquecer en un preorden monoidal V = (V, ≤, I,) significa “dejar que V estructura la cuestión de pasar de a a b”. Todas las estructuras de un preorden monoidal, es decir, el conjunto V, la relación de orden ≤, la unidad monoidal I y el producto monoidal, juegan un papel en la forma en que funciona el enriquecimiento.

Por ejemplo, veamos el caso de Bool = ($\mathbb{B}$, ≤, true,$\wedge$). El hecho de que su conjunto subyacente sea$\mathbb{B}$ = {falso, verdadero} se traducirá en decir que “pasar de a a b es una pregunta verdadera/falsa”. El hecho de que cierto sea la unidad monoidal se traducirá en decir “siempre se puede llegar de una a una”. El hecho de que$\cap$ sea el producto monoidal se traducirá en decir “si puedes obtener de a a b Y puedes obtener de b a c entonces puedes obtener de a a c.” Por último, la forma “si-entonces” de la oración anterior viene de la relación de orden ≤. Esto lo haremos más preciso en la Sección 2.3.

Podremos jugar el mismo juego con otros preordenes monoidales, como veremos después de definir un preorden monoidal llamado Costo en el Ejemplo 2.37.

Algunos otros preordenes monoidales Es un poco impreciso llamar a Bool “el” preorden monoidal booleano, porque hay otra estructura monoidal en ($\mathbb{B}$, ≤), que describimos en el Ejercicio 2.29. La primera estructura, sin embargo, parece ser más útil en la práctica que la segunda.

Ejercicio 2.29.

Sea ($\mathbb{B}$, ≤) como arriba, pero ahora considere que el producto monoidal es$\vee$ (OR).

$Screen Shot 2021-01-05 a las 6.04.24 PM.png$: ¿Cuál debe ser la unidad monoidal para satisfacer las condiciones de la Definición 2.2? ¿Satisface el resto de condiciones? ♦

En el Ejemplo 2.30 y Ejercicio 2.31 damos dos estructuras monoidales diferentes sobre el preorden ($\mathbb{N}$, ≤) de los números naturales, donde ≤ es el orden habitual (0 ≤ 1 y 5 ≤ 16).

Ejemplo 2.30 (Números naturales con suma).

Existe una estructura monoidal en ($\mathbb{N}$, ≤) donde la unidad monoidal es 0 y el producto monoidal es +, es decir, 6 + 4 = 10. Es fácil comprobar que$x_{1}$ ≤$y_{1}$ y$x_{2}$ ≤$y_{2}$ implica$x_{1}$ +$x_{2}$ ≤$y_{1}$ +$y_{2}$, así como todas las demás condiciones de la Definición 2.2.

Ejercicio 2.31.

Mostrar que hay una estructura monoidal en ($\mathbb{N}$, ≤) donde el producto monoidal es ∗, es decir, 6 ∗ 4 = 24. ¿Cuál debería ser la unidad monoidal?

Ejemplo 2.32 (Divisibilidad y multiplicación)

Recordemos del Ejemplo 1.45 que hay un orden de “divisibilidad” en$\mathbb{N}$: escribimos m | n para significar que m se divide en n sin resto. Así 1| m para todos m y 4|12.

Existe una estructura monoidal en ($\mathbb{N}$, |), donde la unidad monoidal es 1 y el producto monoidal es ∗, es decir, 6 ∗ 4 = 24. Entonces si$x_{1}$ |$y_{1}$ y$x_{2}$ |$y_{2}$, entonces ($x_{1}$∗$x_{2}$) | ($y_{1}$∗$y_{2}$).

En efecto, si hay alguna$p_{1}$,$p_{1}$$\in$$\mathbb{N}$ tal que$x_{1}$ ∗$p_{1}$ =$y_{1}$ y$x_{2}$ ∗$p_{2}$ =$y_{2}$, entonces ($p_{1}$∗$p_{2}$) ∗ ($x_{1}$∗$x_{2}$) =$y_{1}$ ∗$y_{2}$.

Ejercicio 2.33.

Nuevamente tomando el orden de divisibilidad ($\mathbb{N}$, |). Alguien propone 0 como unidad monoidal y + como producto monoidal. ¿Esa propuesta satisface las condiciones de la Definición 2.2? ¿Por qué o por qué no?

Ejercicio 2.34.

Considera el preorden (P, ≤) con diagrama de Hasse no → tal vez → sí. Proponemos una estructura monoidal con sí como unidad monoidal y “min” como producto monoidal.

1. Dar sentido al “min” rellenando la tabla de multiplicación con elementos de P.

$Screen Shot 2021-01-05 a las 6.07.22 PM.png$

2. Verifique los axiomas de Definición 2.2 hold para NMY: = (P, ≤, sí, min), dada su definición de min. Si no, cambia tu definición de min.

Ejercicio 2.35.

Sea S un conjunto y que P (S) sea su conjunto de potencia, el conjunto de todos los subconjuntos de S, incluyendo el subconjunto vacío, Ø$\subseteq$ S, y el subconjunto “todo”, S\ (\ subseteq\) S. Podemos darle a P (S) un orden: A ≤ B viene dada por la relación de subconjunto A$\subseteq$ B, como se discute en el Ejemplo 1.50. Proponemos una estructura monoidal simétrica sobre P (S) con unidad monoidal S y producto monoidal dado por intersección A$\land$ B.

¿Cumplen las condiciones de la Definición 2.2? ♦

Ejercicio 2.36.

Dejar$Prop^{N}$ denotar el conjunto de todas las declaraciones matemáticas que uno puede hacer acerca de un número natural, donde consideramos que dos declaraciones son iguales si una es verdadera si y sólo si la otra es verdadera. Por ejemplo “n es primo” es un elemento de$Prop^{N}$, y también lo son “n = 2” y “n ≥ 11”. Las declaraciones “n + 2 = 5” y “n es el primo menos impar” se consideran iguales. Dado P, Q$\in$$Prop^{N}$, decimos P ≤ Q si para todo n$\in$ N, siempre que P (n) sea verdadero, así es Q (n).

Definir una unidad monoidal y un producto monoidal sobre ProPN que satisfagan las condiciones de la Definición 2.2. ♦

El preorden monoidal Costo Como dijimos anteriormente, cuando enriquecemos en preordenes monoidales los vemos como diferentes formas de estructurar la cuestión de “llegar de aquí para allá”. Esto lo explicaremos con más detalle en la Sección 2.3. El siguiente preorden monoidal eventualmente estructurará una noción de distancia o costo para llegar de aquí a allá.

Ejemplo 2.37 (preorden monodial de Lawvere, COST).

Deje que [0, ∞] denote el conjunto de números reales no negativos como 0, 1, 15.333 y 2π junto con ∞. Considera el preorden ([0, ∞], ≥), con la noción habitual de ≥, donde por supuesto ∞ ≥ x para todos x$\in$ [0, ∞].

Hay una estructura monoidal en este preorden, donde la unidad monoidal es 0 y el producto monoidal es +. En particular, x + ∞ = ∞ para cualquier x$\in$ [0, ∞]. Llamemos a este preorden monoidal

Costo := ([0, ∞], ≥, 0, +),

porque podemos pensar en los elementos de [0, ∞] como costos. En términos de estructurar “llegar de aquí para allá”, Cost parece decir “pasar de a a b es una cuestión de costo”. Al ser 0 la unidad monoidal se traducirá en decir que siempre se puede obtener de una a a sin costo alguno. El producto monoidal siendo + se traducirá en decir que el costo de pasar de a a a c es a lo sumo el costo de obtener de a a b más el costo de obtener de b a c. Por último, el “a lo sumo” en la oración anterior viene del ≥.

Lo contrario de un preorden monoidal Uno puede tomar lo contrario de cualquier preorden, simplemente voltear el orden: ((X, ≤)$^{op}$ := (X, ≥); ver Ejemplo 1.58. La Proposición 2.38 dice que si el preorden tenía una estructura monoidal simétrica, también lo hace su opuesto.

Proposición 2.38.

Supongamos que X = (X, ≤) es un preorden y$X^{op}$ = (X, ≥) es su opuesto. Si (X, ≤, I,) es un preorden monoidal simétrico entonces también lo es su opuesto, (X, ≥, I,).

Comprobante. Primero comprobemos la monotonicidad. Supongamos$x_{1}$ $x_{2}$≥$y_{1}$ y ≥$y_{2}$ in$X^{op}$; necesitamos$x_{1}$ mostrar que$x_{2}$$y_{1}$ ≥$y_{2}$. Pero por definición de orden opuesto, tenemos$y_{1}$ ≤$x_{1}$ y$y_{2}$ ≤$x_{2}$ en X, y por$y_{1}$ lo tanto$y_{2}$$x_{1}$ ≤$x_{2}$ en X. Así$x_{1}$ pues efectivamente$x_{2}$$y_{1}$ ≥$y_{2}$ in$X^{op}$.

Las otras tres condiciones son aún más fáciles; ver Ejercicio 2.39. □

Ejercicio 2.39.

Completar el comprobante de la Proposición 2.38 comprobando que se cumplen las tres condiciones restantes de la Definición 2.2.

Ejercicio 2.40.

Dado que el costo es un preorden monoidal simétrico, la Proposición 2.38 dice que eso también lo$Cost^{op}$ es.

¿Qué es$Cost^{op}$ como preorder?
¿Cuál es su unidad monoidal?
Cuál es su producto monoidal

Mapas monófocos monoidales

Recordemos del Ejemplo 1.49 que para cualquier preorden (X, ≤), existe una relación de equivalencia inducida$\cong$ en X, donde x$\cong$ x ′ iff tanto x ≤ x ′como x ′ ≤ x.

Definición: 2.41.

Sea P = (P,$≤_{P}$,$I_{P}$,$⊗_{P}$) y Q = (Q,$≤_{Q}$,$I_{Q}$,$⊗_{Q}$) preordenes monoidales. Un monótona monoidal de P a Q es un mapa monótono f: (P,$≤_{P}$) → (Q,$≤_{Q}$), que satisface dos condiciones:

(a)$I_{Q}$$≤_{Q}$ f ($I_{P}$), y

b$p_{1}$) f$⊗_{Q}$ f f$p_{2}$$≤_{Q}$ f$p_{1}$$⊗_{P}$$p_{2}$ f

para todos$p_{1}$,$p_{2}$$\in$ P.

Hay fortalecimientos de estas condiciones que también son importantes. Si f satisface las siguientes condiciones, se llama monótona monoidal fuerte:

(a')$I_{Q}$$\cong$ f ($I_{P}$), y

b') f () f ($p_{1}$)$⊗_{Q}$ f ($p_{2}$) f ($p_{1}$$⊗_{P}$$p_{2}$);

y si satisface las siguientes condiciones se le llama monótona monoidal estricta:

(a”)$I_{Q}$ = f ($I_{P}$), y

b”) f ($p_{1}$)$⊗_{Q}$ f ($p_{2}$) = f ($p_{1}$$⊗_{P}$$p_{2}$).

Los monótonos monoidales son ejemplos de funtores monoidales, de los cuales veremos diversas encarnaciones a lo largo del libro; ver Definición 6.68. Lo que llamamos monótonos monoidales también podría llamarse monótonos monoidales laxos, y existe una noción dual de monótonos monoidales oplax, donde se revierten las desigualdades en (a) y (b); no usaremos la oplaxidad en este libro.

Ejemplo 2.42.

Hay una monótona monoidal i: ($\mathbb{N}$, ≤, 0, +) → ($\mathbb{R}$, ≤, 0, +), donde i (n) = n para todos n$\in$$\mathbb{N}$. Es claramente monótona, m ≤ n implica i (m) ≤ i (n). Incluso es monoidal estricto porque i (0) = 0 e i (m + n) = i (m) + i (n). También hay una monótona monoidal f: ($\mathbb{R}$, ≤, 0, +) → ($\mathbb{N}$, ≤, 0, +) yendo hacia el otro lado. Aquí f (x) := x es la función floor, por ejemplo f (3.14) = 3. Es monótona porque x ≤ y implica f (x) ≤ f (y). También f (0) = 0 y f (x) + f (y) ≤ f (x + y), por lo que es un monótona monoidal. Pero no es estricto ni siquiera fuerte porque f (0.5) + f (0.5)$\neq$ f (0.5 + 0.5).

Recordemos Bool = ($\mathbb{B}$, ≤, true,$\wedge$) del Ejemplo 2.27 y Costo: = ([0, ∞], ≥, 0, +) del Ejemplo 2.37. Hay una monótona monoidal g: Bool → Costo, dada por g (false) := ∞ y g (true) := 0.

Ejercicio 2.43.

1. Verifique que el mapa g: ($\mathbb{B}$, ≤, true,$\wedge$) → ([0, ∞], ≥, 0, +) presentado anteriormente efectivamente

es monótona,
satisfaga la condición (a) de la definición 2.41, y
satisface la condición (b) de la Definición 2.41.

2. ¿Es g estricto? ♦

Ejercicio 2.44.

Deje que Bool y Cost sean los anteriores, y considere las siguientes funciones cuasiinversas d, u: [0, ∞] → B definidas de la siguiente manera:

$Screen Shot 2021-01-05 at 6.28.31 PM.png$

¿Es d monótona?
¿Cumpla d las condiciones (a) y (b) de la Definición 2.41?
¿Es d estricto?
¿Es u monotónico?
¿Cumpla u las condiciones (a) y (b) de la Definición 2.41?
¿Es u estricto? ♦

Ejercicio 2.45.

Es ($\mathbb{N}$, ≤, 1, ∗) un preorden monoidal, donde ∗ es la multiplicación habitual de números naturales?
Si no, ¿por qué no? Si es así, ¿existe un monótona monoidal ($\mathbb{N}$, ≤, 0, +) → ($\mathbb{N}$, ≤, 1, ∗)? Si no; ¿por qué no? Si es así, encuéntralo.
¿Es ($\mathbb{Z}$, ≤, ∗, 1) un preorden monoidal? ♦