5.1: Comparar sistemas como procesadores de señal que interactúan

Los sistemas ciberfísicos son sistemas que involucran partes físicas y computacionales estrechamente interactuando. Un ejemplo es un automóvil autónomo: los sensores informan a un sistema de decisión que controla una unidad de dirección que conduce un automóvil, cuyo movimiento cambia la entrada sensorial. Si bien dichos sistemas implican interacciones complejas de muchos subsistemas diferentes, tanto físicos, como el accionamiento de una rueda por un motor, o un voltaje colocado a través de un cable, como computacionales, como un programa que toma una velocidad medida y devuelve una aceleración deseada, a menudo es útil modelar el comportamiento del sistema como simplemente el paso y procesamiento de señales. Para este boceto ilustrativo, solo pensaremos en las señales como cosas que podemos sumar y multiplicar, como los números reales.

La interacción en los sistemas ciberfísicos a menudo se puede entender como un intercambio de variables; es decir, cuando dos sistemas están vinculados, ciertas variables se comparten. Por ejemplo, cuando conectamos dos vagones de tren mediante un acoplamiento físico, los vagones del tren deben tener la misma velocidad, y sus posiciones difieren en una constante. De igual manera, cuando conectamos dos puertos eléctricos, los potenciales eléctricos en estos dos puertos ahora deben ser los mismos, y la corriente que fluye hacia uno debe ser igual a la corriente que fluye fuera del otro. Por supuesto, la forma en que se usa realmente la variable compartida puede ser muy diferente para los diferentes subsistemas que la utilizan, pero compartir la variable sirve para acoplar esos sistemas, no obstante.

Obsérvese que ambos ejemplos anteriores implican la unión física de dos sistemas; más figurativamente, podríamos expresar la interconexión dibujando una línea que conecta las cajas que representan los sistemas. En su forma más simple, esto es captado por el formalismo de las gráficas de flujo de señal, debido a Claude Shannon en la década de 1940. Aquí hay un ejemplo de un gráfico de flujo de señal:

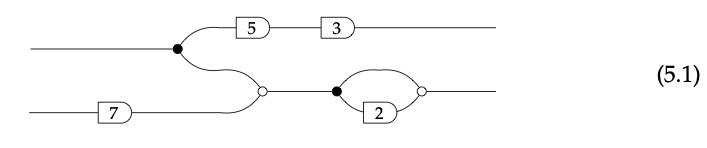
Consideramos los cables colgados de la izquierda como entradas, y los de la derecha como salidas. En la Ec. (5.1) vemos tres tipos de unidades de procesamiento de señal, las cuales interpretamos de la siguiente manera:

• Cada unidad etiquetada por un número a toma una entrada y la multiplica por a.
• Cada punto negro toma una entrada y produce dos copias del mismo.
• Cada punto blanco toma dos entradas y produce su suma.

Así, el gráfico de flujo de señal anterior toma dos señales de entrada, digamos x (en el cable superior izquierdo) e y (en el cable inferior izquierdo), y, yendo de izquierda a derecha como se describió anteriormente produce dos señales de salida: u = 15 x (superior derecha) y v = 3 x + 21 y (inferior derecha). Vamos a mostrar algunos pasos de este cálculo (dejando a otros fuera para evitar el desorden):

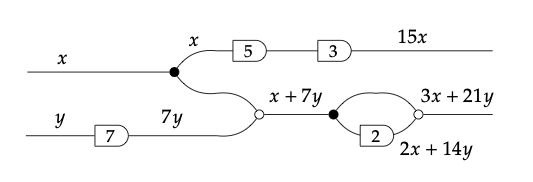
En palabras, el gráfico de flujo de señal primero multiplica y por 7, luego divide x en dos copias, agrega la segunda copia de x a la señal inferior para obtener x + 7 y, y así sucesivamente.

Un gráfico de flujo de señal podría describir un sistema existente, o podría especificar un sistema a construir. En cualquier caso, es importante poder analizar estos diagramas para entender cómo el sistema compuesto convierte las entradas en salidas. Esto es una reminiscencia de un problema de co-diseño del Capítulo 4, que pregunta cómo evaluar la relación de factibilidad compuesta a partir de un diagrama de relaciones de factibilidad más simples. Podemos usar este proceso de evaluación para determinar si dos gráficas de flujo de señal diferentes especifican de hecho el mismo sistema compuesto y, por lo tanto, para validar que un sistema cumple con una especificación dada.

En este capítulo, sin embargo, introducimos herramientas categóricas —props y sus presentaciones para razonar más directamente con los diagramas. Recordemos del Capítulo 2 que los preordenes monoidales simétricos son un tipo de categoría monoidal simétrica donde los morfismos están limitados a ser muy simples: puede haber a lo sumo un morfismo entre dos objetos cualesquiera. Aquí verá que los gráficos de flujo de señal representan morfismos en una simplificación diferente y complementaria del concepto de categoría monoidal simétrica, conocido como prop .1 Un prop es una categoría monoidal simétrica donde los objetos están restringidos a ser muy simples: se generan, utilizando el producto monoidal, por un solo objeto.

Así como los diagramas de cableado para prepedidos monoidales simétricos no requerían etiquetas en las cajas, esto significa que los diagramas de cableado para accesorios no requieren etiquetas en los cables. Esto hace que los apoyos sean particularmente adecuados para describir formalismos diagramáticos como gráficos de flujo de señal, que solo tienen cables de un solo tipo.

Finalmente, muchos sistemas se comportan de lo que se llama una forma lineal, y los sistemas lineales forman una parte fundamental de la teoría del control, una rama de la ingeniería que trabaja en sistemas ciberfísicos. Del mismo modo, el álgebra lineal es una parte fundamental de las matemáticas modernas, tanto puras como aplicadas, que incluye no sólo la teoría del control, sino también la práctica de la computación, la física, la estadística y muchos otros. Al analizar los gráficos de flujo de señal, veremos que de hecho son una forma de refundir álgebra lineal, más específicamente, operaciones matriciales, en términos gráficos. De manera más formal, diremos que las gráficas de flujo de señal tienen semántica funcionaria como matrices.