6.1: La ubicuidad de los lenguajes de red

Circuitos eléctricos, redes de reacción química, autómatas de estado finito, procesos de Markov: todos estos son modelos de sistemas físicos o computacionales que comúnmente se describen mediante diagramas de red. Aquí, por ejemplo, dibujamos un diagrama que modela un flip-flop, un circuito eléctrico importante en la memoria de la computadora que puede almacenar un poco de información:

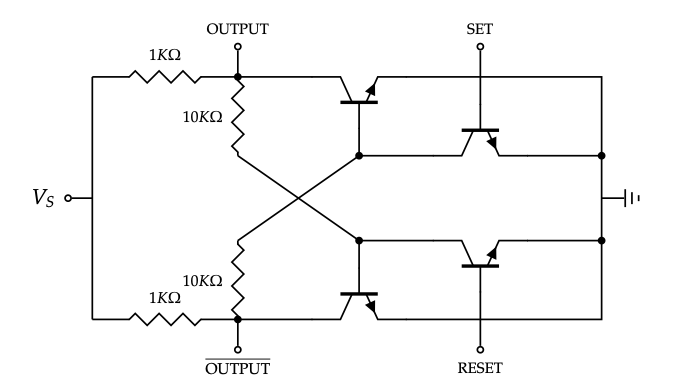
Los diagramas de red tienen utilidad probada en el tiempo. En este capítulo, nos interesa entender la estructura matemática común que comparten, con el propósito de traducirlos y unificarlos; por ejemplo, ciertos tipos de procesos de Markov pueden simularse y, por ende, resolverse utilizando circuitos de resistencias. Cuando entendemos las estructuras subyacentes que son compartidas por lenguajes de diagrama de red, podemos hacer comparaciones entre los modelos matemáticos correspondientes fácilmente.

A primera vista los diagramas de red aparecen bastante diferentes de los diagramas de cableado que hemos visto hasta ahora. Por ejemplo, los cables están desdirigidos en el caso anterior, mientras que en una categoría que incluye categorías monoidales vistas en teorías de recursos o codiseño cada morfismo tiene un dominio y un codominio, dándole un sentido de dirección. Sin embargo, veremos cómo usar construcciones categóricas como las propiedades universales para crear modelos categóricos que capturen con precisión el tipo de composicionalidad “red” anterior, es decir, permitiéndonos caer efectivamente la direccionalidad cuando sea conveniente.

En particular volveremos a la idea de un colimit, que esbozamos para ti al final del Capítulo 3, y mostraremos cómo usar los corlimits en la categoría de conjuntos para formalizar ideas de conexión. Aquí está la idea clave.

Conexiones a través de corlimites. Digamos que queremos instalar algunas luces: queremos crear un circuito para que cuando disparemos un interruptor, una luz se encienda o apague. Para comenzar, tenemos un montón de componentes de circuito: una fuente de alimentación, un interruptor y una lámpara conectada a una resistencia:

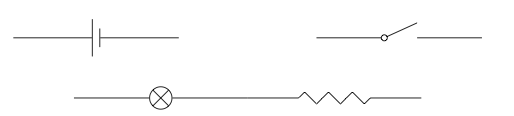
Queremos conectarlos entre sí, pero hay muchas formas de hacerlo. ¿Cómo debemos describir la forma particular que formará un interruptor de luz?

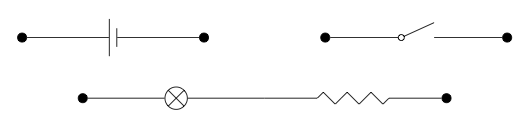
En primer lugar, afirmamos que los circuitos realmente deben ser pensados como circuitos abiertos: cada uno lleva la estructura adicional de una 'interfaz' exponiéndola al resto del mundo eléctrico. Aquí por interfaz nos referimos a cierto conjunto de ubicaciones, o puertos, en los que somos capaces de conectarlos con otros componentes.1 Como es tan común en la teoría de categorías, comenzamos por hacer explícito este hecho más o menos obvio. Representemos los puertos disponibles usando un • en negrita. Si decimos que en cada uno de los tres dibujos anteriores, los puertos son simplemente los puntos finales colgados de los cables, se volverían a dibujar de la siguiente manera:

A continuación, tenemos que describir qué puertos deben estar conectados. Esto lo haremos dibujando círculos vacíos ◦ conectados por flechas a dos puertos •. Cada uno será una conexión de testigo a-, diciendo '¡conecta estos dos!'

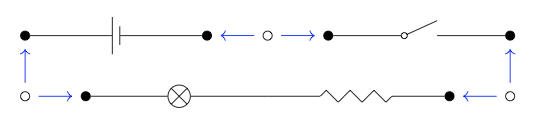
Al mirar esta imagen, queda claro lo que tenemos que hacer: simplemente identificar —es decir, fusionar o hacer iguales —los puertos como se indica, para obtener el siguiente circuito:

Pero las matemáticas no tienen una corteza visual con la que generar las intuiciones con las que podamos contar con un lector humano como tú. \(^{2}\)Por lo tanto, necesitamos especificar formalmente qué significa matemáticamente 'identificar puertos como indicados'. Resulta que podemos hacer esto usando corlímites finitos en una determinada categoría C.

Los colímites son diagramas con ciertas propiedades universales, lo que es una especie de epife-nomenon de la categoría C. Nuestro objetivo es obtener los corlímites de C de manera más directa, como una especie de operación en algún contexto, para que podamos pensar en ellos como decirnos cómo conectar partes del circuito entre sí. Para ello, producimos una cierta categoría monoidal a saber, la de cospanes en C, denotada como Cospan\(_{C}\) que puede empaquetar convenientemente los corlímites de C en términos de sus propias operaciones básicas: composición y producto monoidal.

En resumen, la primera parte de este capítulo está dedicada al lema 'colimits model interconexión'. Además de las construcciones universales como los colímites, sin embargo, otra forma de describir la interconexión es usar diagramas de cableado. Vamos al círculo completo cuando nos encontramos con que estos diagramas de cableado están fuertemente conectados a los cospanes, y de ahí a los colímites.

Pero las matemáticas no tienen una corteza visual con la que generar las intuiciones con las que podamos contar con un lector humano como usted mismo.2 Así que necesitamos especificar formalmente qué significa matemáticamente 'identificar puertos como se indican'. Resulta que podemos hacer esto usando corlímites finitos en una determinada categoría C.

Los colímites son diagramas con ciertas propiedades universales, lo que es una especie de epife-nomenon de la categoría C. Nuestro objetivo es obtener los corlímites de C de manera más directa, como una especie de operación en algún contexto, para que podamos pensar en ellos como decirnos cómo conectar partes del circuito entre sí. Para ello, producimos una cierta categoría monoidal a saber, la de cospanes en C, denotada como Cospan\(_{C}\) que puede empaquetar convenientemente los corlímites de C en términos de sus propias operaciones básicas: composición y producto monoidal.

En resumen, la primera parte de este capítulo está dedicada al lema 'colimits model interconexión'. Además de las construcciones universales como los colímites, sin embargo, otra forma de describir la interconexión es usar diagramas de cableado. Vamos al círculo completo cuando nos encontramos con que estos diagramas de cableado están fuertemente conectados a los cospanes, y de ahí a los colímites.

Operaciones de composición y diagramas de cableado. En este libro hemos visto la utilidad de definir estructuras sintácticas o algebraicas que describen el tipo de op- eraciones de composición que tienen sentido y pueden realizarse en un área de aplicación determinada. Los ejemplos incluyen preordenes monoidales con descartes, accesorios y categorías cerradas compactas. Cada uno de estos tiene un tipo asociado de estilo de diagrama de cableado, de modo que cualquier dia-gramo de cableado de ese estilo representa una operación de composición que tiene sentido en el área dada: la primera tiene sentido en la fabricación, la segunda en el flujo de señal y la tercera en el diseño colaborativo. Entonces nuestro segundo objetivo es responder a la pregunta, “¿cómo describimos la estructura compositiva de los diagramas de cableado estilo red?”

La interconexión de tipo red se puede describir usando algo llamado categoría hiper- gráfica. En términos generales, se trata de categorías cuyos diagramas de cableado son los de categorías monoidales simétricas junto con, para cada par de números naturales (m, n), un icono s\(_{m,n}\): m → n. Estos iconos, conocidos como arañas,\(^{3}\) se dibujan de la siguiente manera:

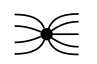
Dos arañas pueden compartir una pierna, y cuando lo hacen, podemos fusionarlas en una sola araña. La intuición es que las arañas son puntos de conexión para una serie de cables, y cuando se conectan dos puntos de conexión, se fusionan para formar un punto de conexión aún más 'connect-y'. Aquí hay un ejemplo:

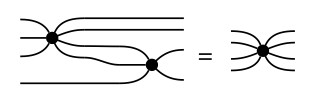
Una categoría de hipergrafía puede tener muchas especies de arañas con la regla de que las arañas de diferentes especies no pueden compartir una pata y por lo tanto no fusionarse sino que dos arañas de la misma especie pueden compartir patas y fusionarse. Agregamos diagramas de araña a la iconografía de categorías de hipergrafía.

Como veremos, las ideas de describir la interconexión de redes utilizando colímites y categorías de hipergrafía se unen en la noción de una teoría. Primero introdujimos la idea de una teoría en la Sección 5.4.2, pero aquí la exploramos más a fondo, comenzando con la idea de que, aproximadamente hablando, los cospanes en la categoría FinSet forman la teoría de las categorías de hipergrafía.

Podemos ensamblar todos los cospans en FinSet en algo llamado 'operad'. A través de este libro hemos hablado sobre el uso de estructuras y presentaciones libres para crear instancias de estructuras algebraicas como preordenes, categorías y accesorios, adaptados a las necesidades de una situación particular. Los óperas se pueden utilizar para adaptar las propias estructuras algebraicas a las necesidades de una situación particular. Discutiremos cómo funciona esto, en particular cómo las óperas codifican varios tipos de lenguajes de diagramas de cableado y estructuras algebraicas correspondientes, al final del capítulo.