6.2: Colímites y conexión
- Page ID
- 112234
Las construcciones universales son fundamentales para la teoría de categorías. Permiten definir objetos, al menos hasta isomorfismo, describiendo su relación con otros objetos. Hasta el momento hemos visto este tema en varias formas diferentes: encuentros y uniones (Sección 1.3), conexiones y adjuntos de Galois (Secciones 1.4 y 3.4), límites (Sección 3.5), y estructuras libres y presentadas (Sección 5.2.3-5.2.5). Aquí dirigimos nuestra atención a los colímites.
En esta sección, nuestra tarea principal es tener una comprensión concreta de los corlimits en la categoría finSet de conjuntos finitos y funciones. La idea será tomar un montón de conjuntos digamos dos o quince o cero usar funciones entre ellos para designar que los elementos en un conjunto 'deben considerarse los mismos' como elementos en otro conjunto, y luego fusionar los conjuntos en consecuencia.
Objetos iniciales
Así como el límite más simple es un objeto terminal (ver Sección 3.5.1), el colímite más simple es un objeto inicial. Este es el caso en el que comienzas sin objetos y los fusionas.
Que C sea una categoría. Un objeto inicial en C es un objeto Ø\(\in\) C tal que por cada objeto T en C existe un morfismo único! \(_{T}\): Ø → T.
El símbolo Ø es solo un nombre por defecto, una notación, destinada a evocar la idea correcta; ver Ejemplo 6.4 por la razón por la que usamos la notación Ø, y Ejercicio 6.7 para un caso en el que probablemente no se usaría el nombre predeterminado Ø.
Nuevamente, el sello distintivo de la universalidad es la existencia de un mapa único a cualquier otro objeto comparable.
Un objeto inicial de un preorden es un elemento inferior es decir, un elemento que es menor que cualquier otro elemento.
Por ejemplo 0 es el objeto inicial en (\(\mathbb{N}\), ≤), mientras que (\(\mathbb{R}\), ≤) no tiene ningún objeto inicial.
Considera el conjunto A = {a, b}. Encuentre una relación de preorden ≤ en A tal que
1. (A, ≤) no tiene objeto inicial.
2. (A, ≤) tiene exactamente un objeto inicial.
3. (A, ≤) tiene dos objetos iniciales. ♦
El objeto inicial en FinSet es el conjunto vacío. Dado cualquier conjunto finito T, existe una función única Ø → T, ya que Ø no tiene elementos.
Como se ve en el Ejercicio 6.3, una categoría C no necesita tener un objeto inicial. Como otro tipo de ejemplo, considere la categoría que se muestra aquí:
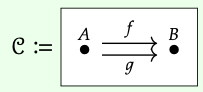
Si hubiera un objeto inicial Ø, sería A o B.
De cualquier manera, necesitamos mostrar que para cada objeto T\(\in\) Ob (C) (es decir, tanto para T = A como T = B) hay un morfismo único Ø → T. Intentando el caso Ø =\(^{?}\) A esta condición falla cuando T = B: hay dos morfismos A → B, no uno.
Y probando el caso Ø =\(^{?}\) B esta condición falla cuando T = A: hay cero morfismos B → A, no uno.
Para cada una de las gráficas a continuación, considere la categoría libre en esa gráfica, y diga si tiene un objeto inicial.

Recordemos la noción de plataforma del Capítulo 5.
Un homomorfismo de plataforma de (R, 0\(_{R}\), +\(_{R}\), 1\(_{R}\), ∗\(_{R}\)) a (S, 0\(_{S}\), +\(_{S}\), 1\(_{S}\), ∗\(_{S}\)) es una función f: R → S tal que f (0\(_{R}\)) = 0 \(_{S}\), f (r 1 +\(_{R}\) r 2) = f (r 1) +\(_{S}\) f (r 2), etc.
1. Dijeron “etc.” Adivina las condiciones restantes para que f sea un homomorfismo de plataforma.
2. Que Rig denote la categoría cuyos objetos son plataformas y cuyos morfismos son homomorfismos de plataforma. Afirmamos que Rig tiene un objeto inicial. ¿Qué es? ♦
Explique la afirmación “el sello distintivo de la universalidad es la existencia de un mapa único a cualquier otro objeto comparable”, en el contexto de la Definición 6.1. En particular, ¿qué es lo que está siendo universal en la Definición 6.1, y cuál es el “objeto comparable”? ♦
OBSERVACIÓN 6.9. Como se menciona en la observación 3.85, a menudo hablamos de 'el' objeto que satisface una propiedad universal, como 'el objeto inicial', a pesar de que muchos objetos diferentes podrían satisfacer la condición inicial del objeto. Nuevamente, la razón es que los objetos iniciales son únicos hasta el isomorfismo único: dos objetos iniciales cualesquiera tendrán entre ellos un isomorfismo canónico, que se encuentra utilizando diversas aplicaciones de la propiedad universal.
Sea C una categoría, y supongamos que c\(_{1}\) y c\(_{2}\) son objetos iniciales. Encuentra un isomorfismo entre ellos, utilizando la propiedad universal de la Definición 6.1. ♦
Coproductos
Los coproductos generalizan tanto uniones en un preorden como uniones disjuntas de conjuntos.
Que A y B sean objetos en una categoría C.
Un coproducto de A y B es un objeto, que denotamos A + B, junto con un par de morfismos (ι\(_{A}\): A → A + B, ι\(_{B}\): B → A + B) tal que para todos los objetos T y pares de morfismos (f: A → T, g: B → T), existe un morfismo único [f, g]: A + B → T tal que el siguiente diagrama conmuta:
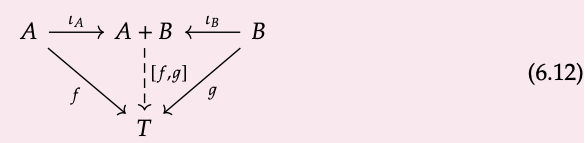
Llamamos [f, g] el copaireo de f y g.
Explique por qué, en un prepedido, los coproductos son lo mismo que las uniones. ♦
Los coproductos en las categorías FinSet y Set son uniones disjuntas. Más precisamente, supongamos que A y B son conjuntos.
Entonces el coproducto de A y B viene dado por la unión disjunta A B junto con las funciones de inclusión ι\(_{A}\): A → A B y ι\(_{B}\): B → A B.
Supongamos que tenemos las funciones f: A → T y g: B → T para algún otro conjunto T, sin foto. La propiedad universal de los coproductos dice que hay una función única [f, g]: A B → T tal que ι\(_{A}\); [f, g] = f y ι\(_{B}\); [f, g ] = g.
¿Qué es? Cualquier elemento x\(\in\) A B es ya sea 'de A 'o 'de B', es decir, o bien hay algo a \(\in\)A con x = ι\(_{A}\) (a) o hay algo de b\(\in\) B con x = ι\(_{B}\) (b). Por la Ec. (6.12), debemos tener:
\ ([f, g] (x) =\ left\ {\ begin {array} {ll}
f (x) &\ text {if} x=\ iota_ {A} (a)\ text {para algunos} a\ in A\
g (x) &\ text {if} x=\ iota_ {B} (b)\ text {para algunos} b\ en B
\ end {array}\ derecho.\)
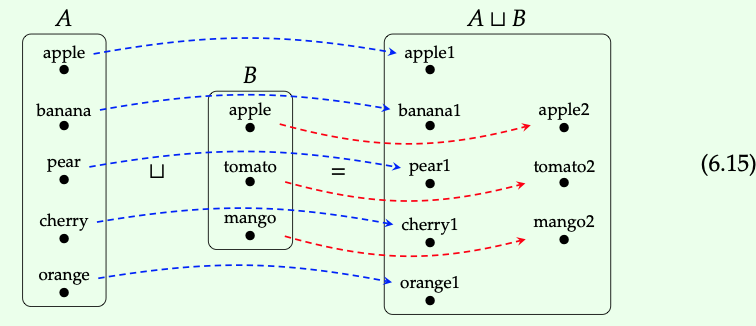
Supongamos que T = {a, b, c,.., z} es el conjunto de letras en el alfabeto, y deja que A y B sean los conjuntos de la Eq. (6.15). Considera la función f: A → T enviando cada elemento de A a la primera letra de su etiqueta, por ejemplo f (manzana) = a. Sea g: B → T la función que envía cada elemento de B a la última letra de su etiqueta, por ejemplo g (manzana) = e. Anote la función [f, g] (x) para los ocho elementos de A B. ♦
Que f: A → C, g: B → C, y h: C → D sean morfismos en una categoría C con coproductos. Demostrar que
1. ι\(_{A}\); [f, g] = f.
2. ι\(_{B}\); [f, g] = g.
3. [f, g]; h = [f; h, g; h].
4. [ι\(_{A}\), ι\(_{B}\)] = id\(_{A+B}\). ♦
Supongamos que una categoría C tiene coproductos, denotados +, y un objeto inicial, denotado Ø. Entonces (C, +, Ø) es una categoría monoidal simétrica (recordar Definición 4.45). En este ejercicio desarrollamos los datos relevantes para este hecho:
1. Mostrar que + se extiende a un functor C × C → C. En particular, ¿cómo actúa sobre los morfismos en C × C?
2. Utilizando las propiedades universales del objeto inicial y coproducto, muestran que existen isomorfismos A + Ø → A y Ø + A → A.
3. Utilizando la propiedad universal del coproducto, anotar morfismos
a) (A + B) + C → A + (B + C).
b) A + B → B + A.
Si quieres, comprueba que estos son isomorfismos.
Entonces se puede comprobar que estos datos obedecen a los axiomas de una categoría monoidal simétrica, pero aquí terminaremos el ejercicio. ♦
Pushouts
Los pushouts son una forma de combinar conjuntos. Al igual que una unión de subconjuntos, un pushout puede combinar dos conjuntos de una manera no disjunta: los elementos de un conjunto pueden identificarse con elementos del otro. La construcción pushout, sin embargo, es mucho más general: permite (y requiere) que el usuario especifique exactamente qué elementos se identificarán. Veremos una demostración de esta generalidad adicional en el Ejemplo 6.29
Que C sea una categoría y que f: A → X y g: A → Y sean morfismos en C que tengan un dominio común. El pushout X +\(_{A}\) Y es el colímite del diagrama
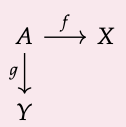
Con más detalle, un pushout consiste en (i) un objeto X +\(_{A}\) Y y (ii) morfismos ι\(_{X}\): X → X +\(_{A}\) Y e i\(_{Y}\): Y → X +\(_{A}\) Y satisfactorias a) y b) que figuran a continuación.
a) El diagrama

desplazamientos. (Vamos a explicar el símbolo '\(\Gamma\)' a continuación.)
(b) Para todos los objetos T y morfismos x: X → T, y: Y → T, si el diagrama
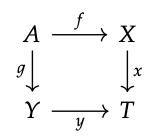
conmuta, entonces existe un morfismo único t: X +\(_{A}\) Y → T tal que
desplazamientos.
Si X +\(_{A}\) Y es un pushout, denotamos ese hecho dibujando el cuadrado conmutativo Eq. (6.20), junto con el\(\Gamma\) símbolo como se muestra; lo llamamos cuadrado pushout. Además, llamamos\(_{X}\) el pushout de g a lo largo de f, y de manera similar,\(_{Y}\) el pushout de f a lo largo de g.
En un preorden, los pushouts y los coproductos tienen mucho en común. El pushout de un diagrama B ← A → C es igual al coproducto B C: es decir, ambos son iguales a la unión B\(\bigvee\) C.
Que f: A → X sea un morfismo en una categoría C. Para cualquier isomorfismos i: A → A ′ y j: X → X ′, podemos tomar X ′ para ser el pushout X +\(_{A}\) A ′, es decir, el siguiente es un cuadrado de salida:
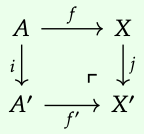
donde f': = i\(^{-1}\); f; j. Para ver esto, observe que si hay algún objeto T tal que la siguiente plaza conmuta:
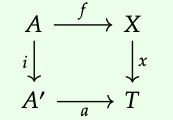
entonces f; x = i; a, y así nos vemos obligados a tomar x': X → T para ser x': = j\(^{-1}\); x. Esto hace que el siguiente diagrama viaje:
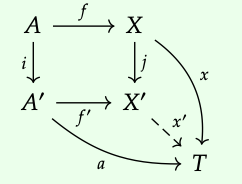
porque f'; x' = i\(^{-1}\); f; j; j\(^{-1}\); x = i\(^{-1}\); i; a = a.
Para cualquier conjunto S, tenemos la categoría discreta Disc\(_{S}\), con S como objetos y solo morfismos de identidad.
1. Mostrar que todos los pushouts existen en Disco\(_{S}\), para cualquier conjunto S.
2. ¿Para qué conjuntos S\(_{S}\) tiene Disc un objeto inicial? ♦
En la categoría FinSet, siempre existen los pushouts. El pushout de las funciones f: A → X y g: A → Y es el conjunto de clases de equivalencia de X Y bajo la relación de equivalencia generada por es decir, el cierre reflexivo, transitivo, simétrico del relación {f (a) ∼ g (a) | a\(\in\) A}.
Podemos pensar en esto también en términos de interconexión. Cada elemento a\(\in\) A proporciona una conexión entre f (a) en X y g (a) en Y.
El pushout es el conjunto de componentes conectados de X Y.
¿Cuál es el pushout de las funciones f:\(\underline{4}\) →\(\underline{5}\) y g:\(\underline{4}\) → que\(\underline{3}\) se muestran a continuación?
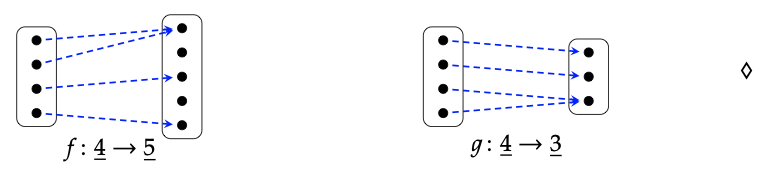
Comprueba tu respuesta usando la descripción abstracta del Ejemplo 6.25.
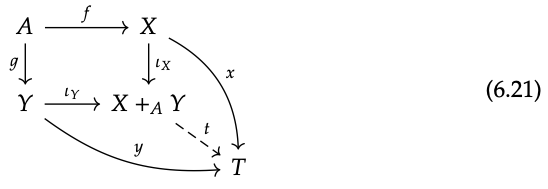
Supongamos que una categoría C tiene un objeto inicial Ø. Para cualquiera de los dos objetos X, Y\(\in\) oBC, hay un morfismo único f: Ø → X y un morfismo único g: Ø → Y; esto es lo que significa que Ø sea inicial.
El diagrama\(X \stackrel{f}{\rightarrow} Ø \stackrel{g}{\leftarrow} Y\) tiene un pushout en C iff X e Y tienen un coproducto en C, y el pushout y el coproducto serán los mismos. En efecto, supongamos que X e Y tienen un coproducto X + Y; luego el diagrama a la izquierda

desplazamientos (¿por qué? \(^{1}\)), y para cualquier objeto T y diagrama conmutativo como a la derecha, hay un mapa único X + Y → T haciendo que el diagrama como en la Eq. (6.21) conmute (¿por qué? \(^{2}\)). Esto demuestra que X + Y es un pushout, X +\(_{Ø}\) Y\(\cong\) X + Y.
De igual manera, si existe un pushout X + Y, entonces satisface la propiedad universal del coproducto (¿por qué? \(^{3}\)).
En Ejemplo 6.27 preguntamos “¿por qué?” tres veces.
1. Dar una justificación para “¿por qué? \(^{1}\)”.
2. Dar una justificación para “¿por qué\(^{2}\)? ”.
3. Dar una justificación para “¿por qué? \(^{3}\)” . ♦
Sea A = X = Y = N. Considera las funciones f: A → X y g: A → Y dadas por las funciones 'piso', f (a) := a /2 y g (a) := (a + 1) /2.
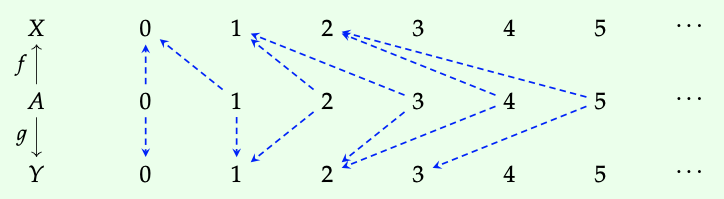
¿Cuál es su pushout? Vamos a averiguarlo usando la definición.
Si T es cualquier otro conjunto y tenemos mapas x: X → T e y: Y → T que conmutan con f y g, es decir, f\(\cong\) x = g\(\cong\) y , entonces esta conmutatividad implica que
y (0) = y (g (0)) = x (f (0)) = x (0).
Es decir, los 0 de Y y los 0 de X van al mismo lugar en T, digamos t. Pero como f (1) = 0 y g (1) = 1, también tenemos que t = x (0) = x (f (1)) = y (g (1)) = y (1). Esto significa que Y's 1 va a t también. Pero como g (2) = 1 y f (2) = 1, también tenemos que t = g (1) = y (g (2)) = x (f (2)) = x (1), lo que significa que el 1 de X también va a t. Uno puede seguir repitiendo esto y encontrar que cada elemento de Y y cada elemento de X van a t! Usando la inducción matemática, se puede probar que el pushout es de hecho un conjunto de 1 elemento, X A Y\(\cong\) {1}.
Colímites finitos
Los objetos iniciales, los coproductos y los pushouts son todo tipo de colímites. Damos la definición general de colimit en la Sección 3.5.4. Así como un límite en C es un objeto terminal en una categoría de conos sobre un diagrama D: J → C, un colímite es un objeto inicial en una categoría de cocones sobre algún diagrama D: J → C. Para nuestros propósitos es suficiente discutir los límites finitos, es decir, cuando J es una categoría finita, que subsume objetos iniciales, coproductos y pushouts. \(^{4}\)
En la Definición 3.102, los cocones en C se definen como conos en\(^{op}\) C. Para fines de visualización, si D: J → C se parece al diagrama de la izquierda, entonces un cocono en él se muestra en el diagrama de la derecha:
Aquí, dos trayectorias paralelas que terminan en T son iguales en C.
Decimos que una categoría C tiene corlímites finitos si existe un colímite, colim\(_{J}\) D, siempre que J es una categoría finita y D: J → C es un diagrama.
¡El objeto inicial en una categoría C, si existe, es el colímite del functor! : 0 → C, donde 0 es la categoría sin objetos y sin morfismos, ¡y! es el único tal functor. En efecto, ¡un cocone terminado! es solo un objeto de C, y así el cocone inicial terminado! es solo el objeto inicial de C.
Tenga en cuenta que 0 tiene finitamente muchos objetos (ninguno); por lo tanto, los objetos iniciales son corlímites finitos.
A menudo queremos saber que una categoría C tiene todos los corlímites finitos (en cuyo caso, a menudo soltamos el 'todo' y solo decimos 'C tiene límites finitos'). Para comprobar que C tiene (todos) corlímites finitos, basta con comprobar que tiene algunas formas más simples de colimit, que generan todo el resto.
Que C sea una categoría. Los siguientes son equivalentes:
1. C tiene todos los corlímites finitos.
2. C tiene un objeto inicial y todos los pushouts.
3. C tiene todos los coecualizadores y todos los coproductos finitos.
Prueba. Aquí no daremos detalles precisos, pero la idea clave es inductiva: se pueden construir diagramas finitos arbitrarios usando algunos bloques básicos de construcción. Los detalles completos se pueden encontrar en [Bor94, Prop 2.8.2]. \(\square\)
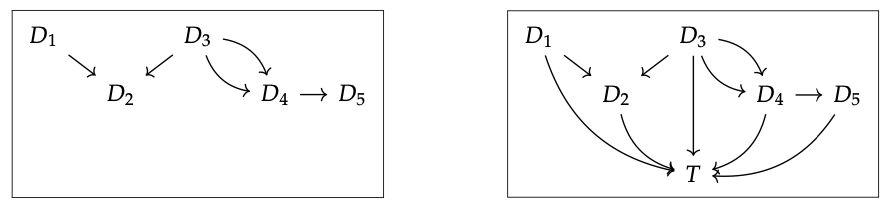
Que C sea una categoría con todos los pushouts, y supongamos que queremos tomar el colimit del siguiente diagrama en C:
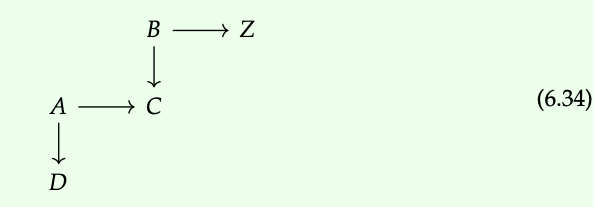
En ella vemos dos diagramas listos para ser empujados, y sabemos cómo tomar pushouts. Entonces supongamos que hacemos eso; luego vemos otro diagrama de pushout así que volvemos a tomar el pushout:
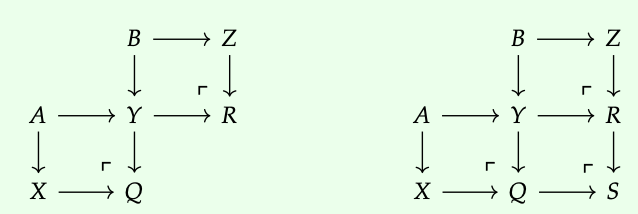
¿el resultado consiste en el objeto S, junto con todos los morfismos desde el diagrama original hasta S el colímite del diagrama original? Se puede comprobar que efectivamente tiene la propiedad universal correcta y por lo tanto es un colimite.
Verifique que el pushout de pushouts del Ejemplo 6.33 satisfaga la propiedad universal del colimit para el diagrama original, Ec. (6.34) . ♦
Ya hemos visto que las categorías FinSet y Set tienen un objeto inicial y pushouts. Tenemos así el siguiente corolario.
Las categorías FinSet y Set tienen (todas) corlímites finitos.
En Teorema 3.95 dimos una fórmula general para computar límites finitos en Set. También es posible dar una fórmula para computar corlímites finitos. Existe una dualidad entre productos y coproductos y entre subobjetos y objetos cocientes, así que mientras que un límite finito viene dado por un subconjunto de un producto, un colímite finito viene dado por un cociente de un coproducto.
Que J sea presentado por la gráfica finita (V, A, s, t) y algunas ecuaciones, y que D: J → Set sea un diagrama. Considera el conjunto
\(\operatorname{colim}_{g} D:=\{(v, d) \mid v \in V \text { and } d \in D(v)\} / \sim\)
donde esto denota el conjunto de clases de equivalencia bajo la relación de equivalencia ∼ generada poniendo (v, d) ∼ (w, e) si hay una flecha a: v → w en J tal que D (a) ( d) = e. Entonces este conjunto, junto con las funciones i\(_{v}\): D (v) → colim\(_{J}\) D dadas al enviar d\(\in\) D (v) a su clase de equivalencia, constituye un colímite de D.
Recordemos que un objeto inicial es el colimit en la gráfica vacía. La fórmula así dice que el objeto inicial en Set es el conjunto vacío Ø: no hay \(\in\)v V.
Un coproducto es un colímite en la gráfica J =\(v_{1} \quad v_{2}\). Un functor D: J → Set se puede identificar con una opción de dos conjuntos, X: = D (v\(_{1}\)) e Y: = D (v\(_{2}\)). Como no hay flechas en J, la relación de equivalencia ∼ es vacía, por lo que la fórmula en el Teorema 6.37 dice que un coproducto viene dado por
\(\left\{(v, d) \mid d \in D(v), \text { where } v=v_{1} \text { or } v=v_{2}\right\}\)
Es decir, el coproducto de los conjuntos X e Y es su unión disjunta X Y, como se esperaba.
Si J es la categoría 1 =\(\begin{array}{l} v \\ \bullet \end{array}\), la fórmula en Teorema 6.37 arroja el conjunto
{(v, d) | d\(\in\) D (v)}
Esto es isomórfico al conjunto D (v). En otras palabras, si X es un conjunto considerado como diagrama X: 1 → Set, entonces su colímite (como su límite) es solo X nuevamente.
Usa la fórmula del Teorema 6.37 para mostrar que los colímites de los pushouts en un diagrama\(X \stackrel{f}{\rightarrow} N \stackrel{g}{\leftarrow} Y\) concuerdan con la descripción que dimos en el Ejemplo 6.25. ♦
Otro tipo importante de colímite finito es el coecualizador. Estos son corlímites sobre la gráfica\(\bullet \rightrightarrows \bullet\) que consisten en dos flechas paralelas.
Considera algún diagrama\(X \underset{q}{\stackrel{f}{\rightrightarrows}} Y\) en esta gráfica en Set. El coecualizador de este diagrama es el conjunto de clases de equivalencia de Y bajo relación de equivalencia generado al declarar y ∼ y ′ siempre que exista x en X tal que f (x) = y y (x) = y ′.
Volvamos al circuito de ejemplo en la introducción para insinuar por qué los corlimits son útiles para la interconexión. Considera la siguiente imagen:
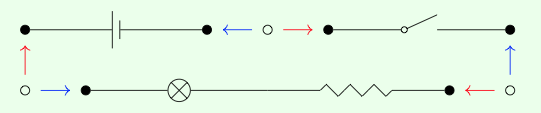
Hemos redibujado esta imagen con un cambio: algunas de las flechas ahora son rojas, y otras ahora son azules. Si dejamos que X sea el conjunto de círculos blancos ◦, e Y sea el conjunto de círculos negros •, las flechas azul y roja definen respectivamente las funciones f, g: X → Y. Dejemos los componentes reales del circuito fuera de escena por ahora; solo nos interesan los puntos. ¿Qué es el coecualizador?
Se trata de un conjunto de tres elementos, que consiste en un elemento por cada par de •'s recién conectados. Así, el colimit describe el conjunto de terminales después de realizar la operación de interconexión. En la Sección 6.4 veremos cómo hacer un seguimiento de los componentes del circuito también.
Cospans
Cuando una categoría C tiene corlímites finitos, una forma extremadamente útil de empaquetarlos es considerando la categoría de cospanes en C.
Que C sea una categoría. Un cospan en C es solo un par de morfismos a un objeto común A → N ← B. El objeto común N se llama el vértice del cospan y los otros dos objetos A y B se llaman sus pies.
Si queremos decir que los cospanes forman una categoría, deberíamos comenzar por decir cómo funcionaría la composición. Entonces supongamos que tenemos dos cospanes en C
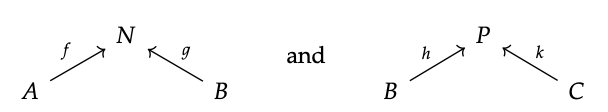
Como el pie derecho del primero es igual al pie izquierdo del segundo, podríamos pegarlos juntos en un diagrama como este:
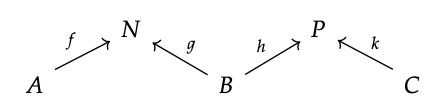
Entonces, si\(N \stackrel{g}{\rightarrow} B \stackrel{h}{\leftarrow} P\) existe un pushout de en C, como se muestra a la izquierda, podemos extraer un nuevo cospan en C, como se muestra a la derecha:
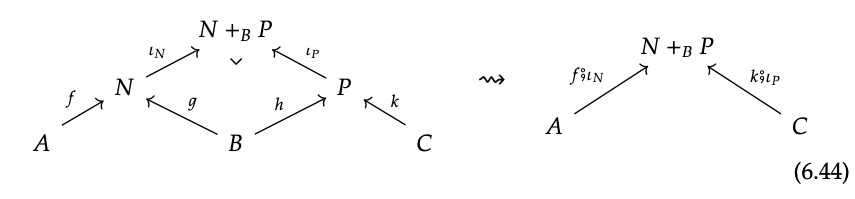
Puede parecer que hemos logrado nuestro objetivo, pero nos faltan algunas cosas. Primero, necesitamos una identidad en cada objeto C\(\in\) Ob C; pero eso no es difícil: usar C → C ← C donde ambos mapas son identidades en C. Más importante aún, no sabemos que C tiene todos los pushouts, así que no sabemos que cada dos morfismos secuenciales A → B → C puede estar compuesto. Y más allá de eso, hay una condición técnica de que cuando formamos pushouts, solo obtenemos una respuesta 'hasta el isomorfismo': cualquier cosa isomórfica a un pushout cuenta como un pushout (revisa la definición para ver por qué). Queremos que todas estas opciones diferentes cuenten como lo mismo, así definimos dos cospanes para que sean equivalentes si hay un isomorfismo entre sus respectivos ápices. Es decir, el cospan A → P ← B y A → P ′ ← B en el diagrama que se muestra a la izquierda a continuación son equivalentes si hay un isomorfismo P\(\cong\) P ′ haciendo que el diagrama a la derecha conmute:

Ahora estamos llegando a alguna parte. Siempre y cuando nuestra categoría C tenga pushouts, estamos en el negocio: Cospan\(_{C}\) formará una categoría. Pero de hecho, estamos muy cerca de conseguir más. Si también exigimos que C tenga un objeto inicial Ø también, entonces podemos actualizar Cospan\(_{C}\) a una categoría monoidal simétrica.
Recordemos de la Proposición 6.32 que una categoría C tiene todos los límites finitos si tiene un objeto inicial y todos los pushouts.
Que C sea una categoría con corlímites finitos. Luego existe una categoría Cospan\(_{C}\) con los mismos objetos que C, es decir, Ob (Cospan\(_{C}\)) = Ob (C), donde los morfismos A → B son las (clases de equivalencia de) cospans de A a B, y la composición viene dada por lo anterior construcción pushout.
Existe una estructura monoidal simétrica en esta categoría, denotada (Cospan\(_{C}\), Ø, +). La unidad monoidal es el objeto inicial Ø\(\in\) C y el producto monoidal viene dado por coproducto. Los isomorfismos de coherencia, por ejemplo \(\cong\)A + Ø A, pueden definirse de manera similar a los del Ejercicio 6.18.
Es un ejercicio sencillo pero lento verificar que (Cospan\(_{C}\), Ø, +) de la Definición 6.45 realmente satisface todos los axiomas de una categoría monoidal simétrica, pero sí.
La categoría FinSet tiene corlímites finitos (ver 6.36). Entonces, podemos definir una categoría monoidal simétrica Cospan\(_{FinSet}\). ¿Qué aspecto tiene? Se parece mucho a cables que conectan puertos.
Los objetos de Cospan\(_{FinSet}\) son conjuntos finitos; aquí vamos a dibujarlos como colecciones de •'s Los morfismos son cospanes de funciones. Que A y N sean cinco conjuntos de elementos, y B sea a\(A \stackrel{f}{\rightarrow} N \stackrel{g}{\leftarrow} B\).
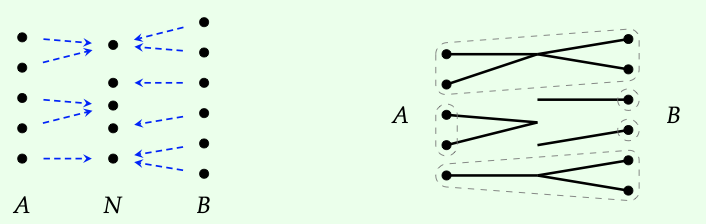
En la representación de la izquierda, simplemente representamos las funciones f y g dibujando flechadesde \(\in\)A a f (a) y cada b\(\in\) B a g (b). En la representación de la derecha, hacemos que esta imagen se parezca un poco más a los cables, simplemente dibujando un alambre donde antes teníamos una flecha, y quitando los puntos centrales innecesarios. También trazamos una línea punteada alrededor de puntos que están conectados, para enfatizar una perspectiva importante, que los cospanes establecen que ciertos puertos están conectados, es decir, parte de la misma clase de equivalencia.
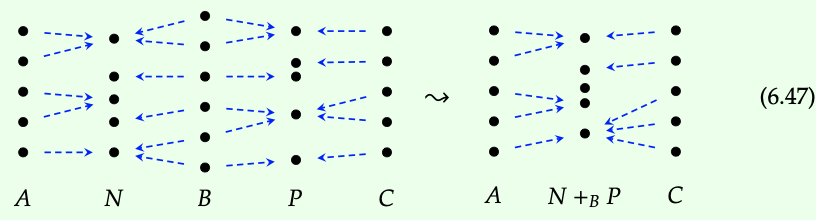
La categoría monoidal Cospan proporciona\(_{FinSet}\) entonces dos operaciones para combinar cospanes: composición y producto monoidal. La composición se da tomando el pushout de los mapas provenientes del pie común, como se describe en la Definición 6.45. Aquí hay un ejemplo de composición de cospan, donde todas las funciones se representan con notación de flecha:
El producto monoidal viene dado simplemente por la unión disjunta de dos cospanes; en imágenes es simplemente combinar dos cospanes apilando uno encima del otro.
En la Ec. (6.47) mostramos morfismos A → B y B → C en Cospan\(_{FinSet}\).
Dibujar su producto monoidal como un morfismo A + B → B + C en Cospan\(_{FinSet}\). ♦
Representar el compuesto de cospanes en la Ec. (6.47) con la notación de alambre da
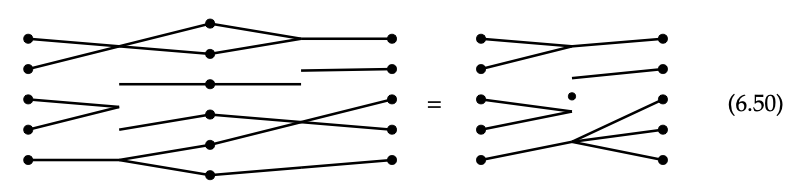
Comparando la Ec. (6.47) y la Ec. (6.50), describen la regla de composición en Cospan\(_{FinSet}\) en términos de cables y componentes conectados. ♦


