7.4: Toposas
- Page ID
- 112344
Toposes
Un topos se define como una categoría de poleas. \(^{9}\)Entonces, para cualquier espacio topológico (X, Op), la categoría Shv (X, Op) definida en la Definición 7.35 es un topos. En particular, tomando el espacio de un punto X = 1 con su topología única, encontramos que la categoría Set es un topos, como venimos diciendo todo el tiempo y vimos nuevamente explícitamente en el Ejemplo 7.48. Y para cualquier esquema de base de datos, es decir, categoría finitamente presentada, C, la categoría C- Inst de instancias de base de datos en C también es un topos.10 Los toposes abarcan ambas fuentes de ejemplos y muchas más.
Las toposas son estructuras increíblemente bonitas, por una variedad de razones aparentemente dispares. En este boceto, la razón en foco es que cada topos tiene muchas de las mismas propiedades estructurales que tiene la categoría Conjunto. En efecto, discutimos en la Sección 7.2.1 que cada topos tiene límites y corlímites, es cartesiano cerrado, tiene factorizaciones epi-mono y tiene un clasificador subobjeto (ver Sección 7.2.2). Usando estas propiedades, se puede hacer lógica con semántica en los topos E. Esto lo explicamos para conjuntos, pero ahora imagínelo para poleas en un espacio topológico. Allí, los mismos símbolos lógicos\(\land\),\(\lor\), ¬, ⇒,, π se convierten en operaciones que significan algo sobre las subpoleas, por ejemplo, campos vectoriales, secciones de funciones continuas, etc., no solo subconjuntos.
Para entender esto más profundamente, debemos decir lo que el clasificador subobjeto true: 1 → Ω es en más generalidad. Dijimos que, en el Conjunto de topos, el clasificador subobjeto es el conjunto de booleanos Ω =\(\mathbb{B}\). En una gavilla topos\(\mathcal{E}\) = Shv (X, Op), el objeto Ω\(\in\)\(\mathcal{E}\) es una gavilla, no solo un conjunto. ¿Qué gavilla es?
El subobjeto clasificador Ω en una gavilla topos
En esta subsección pretendemos comprender el subobjeto clasificador Ω, es decir, el objeto de valores de verdad, en la gavilla topos Shv (X, Op). Ya que Ω es una gavilla, vamos a entenderla pasando por la definición de gavilla (Definición 7.35) lentamente en este caso. Una gavilla Ω es una preheaf que satisface la condición de gavilla.
Como presheaf es solo un functor Ω: Op\(^{op}\) → Set; asigna un conjunto Ω (U) a cada U\(\subseteq\) X abierto y viene con un mapa de restricción Ω (U) → Ω (V) siempre que V\(\subseteq\) U. Entonces, en nuestra búsqueda por entender Ω, primero hacemos la pregunta: ¿qué presheaf es?
La respuesta a nuestra pregunta es que Ω es el presheaf que asigna a U\(\in\) Op el conjunto de subconjuntos abiertos de U:
Ω (U) := {U ′\(\in\) Op | U ′\(\subseteq\) U} . (7.50)
Eso fue fácil, ¿verdad? Y dado el mapa de restricción para V\(\subseteq\) U viene dado por
Ω (U) → Ω (V) (7.51)
U ′\(\longmapsto\) U ′ V.
Se puede comprobar que esto es funciontorial ver Ejercicio 7.53 y después de hacerlo todavía tendremos que ver que satisface la condición de gavilla. Pero al menos no tenemos que luchar para entender Ω: se parece mucho al propio Op.
Sea X = {1} el espacio de un punto. Dijimos anteriormente que su clasificador subobjeto es el conjunto\(\mathbb{B}\) de booleanos, pero ¿cómo se alinea eso con la definición de Ω dada en la Ec. (7.50)? ♦
- Mostrar que la definición de Ω dada anteriormente en las ecuaciones (7.50) y (7.51) es funciontorial, es decir, que siempre que W\(\subseteq\) V\(\subseteq\) U, el mapa de restricción Ω (U) → Ω (V) seguido del mapa de restricción Ω (V) → Ω (W) es lo mismo que el mapa de restricción Ω (U) → Ω (W).
- ¿Eso es todo lo que se necesita para concluir que Ω es un presheaf? ♦
Para ver que Ω como se define en la Ec. (7.50) satisface la condición de gavilla (ver Definición 7.35), supongamos que tenemos una cubierta U =\(\bigcup_{i \in I} U_{i}\), y supongamos dado un elemento V\(_{i}\) \(\in\)Ω (U\(_{i}\)), es decir, un conjunto abierto V\(_{i}\) \(\subseteq\)U\(_{i}\), para cada i\(\in\) yo.
Supongamos además que para todos i, j\(\in\) I, es el caso de que \(_{i}\)V U\(_{j}\) = V\(_{j}\) U\(_{i}\), es decir, que los elementos forman una coincidencia familia.
Definir V: =\(\bigcup_{i \in I} V_{i}\); es un subconjunto abierto de U, por lo que podemos considerar V como un elemento de Ω (U).
Lo siguiente verifica que V es de hecho un pegado para el (V\(_{i}\))\(_{i \in I}\):
\(V \cap U_{j}=\left(\bigcup_{i \in I} V_{i}\right) \cap U_{j}=\bigcup_{i \in I}\left(V_{i} \cap U_{j}\right)=\bigcup_{i \in I}\left(V_{j} \cap U_{i}\right)=\left(\bigcup_{i \in I} U_{i}\right) \cap V_{j}=V_{j}\)
En otras palabras V U\(_{j}\) = V\(_{j}\) para cualquier j\(\in\) I. ¡Así que nuestro Ω ha sido actualizado de preheaf a gavilla!
El lector de ojos de águila habrá notado que aún no hemos dado todos los datos necesarios para definir un clasificador subobjeto. Para convertir el objeto Ω en un clasificador de subobjeto en buen estado, también necesitamos darle un morfismo de gavilla verdadero: {1} → Ω. Aquí {1}: Op\(^{op}\) → Set es la gavilla terminal; mapea cada conjunto abierto a la terminal, un conjunto de elementos {1}.
El correcto morfismo true: {1} → Ω para el clasificador de subobjetos es el morfismo de gavilla que asigna, por cada U\(\in\) Op la función {1} = {1} (U) → Ω (U) enviando 1 → U, el conjunto abierto más grande \(\subseteq\)U U. A partir de ahora denotamos {1} simplemente como 1.
Efecto: Los valores de la verdad son conjuntos abiertos. El punto es que los valores de verdad en los topos de poleas sobre un espacio (X, Op) son los conjuntos abiertos de ese espacio. Cuando alguien dice “¿es verdad la propiedad P? ”, la respuesta no es sí o no, sino “es cierto en el subconjunto abierto U”. Si esta U lo es todo, U = X, entonces P es realmente cierto; si U no es nada, U = Ø, entonces P es realmente falso. Pero en general, es cierto algunos lugares y no otros.
La categoría Grph de grafos es un topos presheaf, y también se puede pensar en ella como la categoría de instancias para un esquema de base de datos, como vimos en el Ejemplo 7.23. El subobjeto clasificador Ω en los topos Gr es así una gráfica, por lo que podemos dibujarla. Así es como se ve:
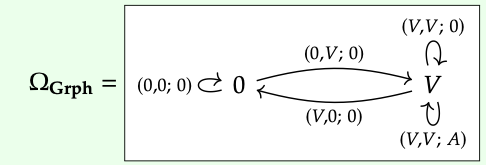
Encontrar Ω para uno mismo es más fácil usando algo llamado el Lema de Yoneda, pero no lo hemos introducido. Para una introducción agradable y fácil a los topos de las gráficas, ver [Vig03]. El gráfico terminal es un solo vértice con un solo bucle, y el gráfico homomorfismo true:1 → Ω envía ese bucle a (V, V; A).
Dada cualquier gráfica G y subgráfica i: H\(\subseteq\) G, necesitamos construir una gráfica homomorfismo\(lceil{H}rceil\): G → Ω clasificando H. La idea es que por cada parte de G, decidamos “cuánto de ella está en H. Un vértice en v en G está o bien en H o no; si es así lo enviamos a V y si no lo enviamos a 0. Pero las flechas a son más complicadas. Si a está en H, lo enviamos (V, V; A). Pero si no está en H, las matemáticas nos obligan a hacer más preguntas: ¿es su fuente en H? es su objetivo en G”? ambos? ¿tampoco? Con base en las respuestas a estas preguntas enviamos a (V, 0; 0), (0, V; 0), (V, V; 0), o (0, 0; 0), respectivamente.
Considera la subgráfica H\(\subseteq\) G que se muestra aquí:

Encuentra la gráfica homomorfismo\(lceil{H}rceil\): G → Ω clasificándolo. Ver Ejemplo 7.54. ♦
7.4.2 Lógica en una gavilla topos
Consideremos las conectivas lógicas, Y, O, IMPLICA, y NO. Supongamos que tenemos un espacio topológico X\(\in\) Op.
Dados dos conjuntos abiertos U, V, considerados como valores de verdad U, V\(\in\) Ω (X), entonces su conjunción 'U Y V' es su intersección, y su disyunción 'U OR V' es su unión;
(U\(land\) V) := U V y (U\(\lor\) V) := U\(\bigcup\) V. (7.56)
Estas fórmulas son fáciles de recordar, porque\(land\) se parece a y\(\lor\) se ve como\(\bigcup\).
La implicación U ⇒ V es el conjunto abierto más grande R tal que R U\(\subseteq\) V, i.e.
\((U \Rightarrow V):=\bigcup_{\left\{R \in \mathbf{O}_{\mathbf{p}} \mid R \cap U \subseteq V\right\}} R .\)(7.57)
En general, no es fácil reducir aún más la ecuación (7.57), por lo que la implicación es el conectivo lógico más difícil de pensar topológicamente.
Por último, la negación de U viene dada por ¬ U: = (U ⇒ false), y esto resulta ser relativamente simple.
Por la fórmula en la Ec. (7.57), es la unión de todos los R tal que R U = Ø, es decir, la unión de todos los conjuntos abiertos en el complemento de U. Si conoces la topología, podrías reconocer que ¬ U es el 'interior del complemento de U'.
Considera la línea real X =\(\mathbb{R}\) como un espacio topológico (ver Ejercicio 7.27).
Sea U, V\(\in\) Ω (X) los conjuntos abiertos U = {x\(\in\) R | x < 3} y V = {x\(\in\)\(\mathbb{R}\) | −4 < x < 4}. Usando notación de intervalo, U = (−∞, 3) y V = (−4, 4). Entonces
• U\(\land\) V = (−4, 3).
• U\(\lor\) V = (−∞, 4).
• ¬ U = (3, ∞).
• ¬ V = (−∞, −4) (4, ∞).
• (U ⇒ V) = (−4, ∞)
• (V ⇒ U) = U
Considera la línea real\(\mathbb{R}\) como un espacio topológico, y considera el subconjunto abierto U =\(\mathbb{R}\) − {0}.
1. ¿Qué subconjunto abierto es ¬ U?
2. ¿Qué subconjunto abierto es ¬¬ U?
3. ¿Es cierto que U\(\subseteq\) ¬¬ U?
4. ¿Es cierto que ¬¬ U\(\subseteq\) U? ♦
Arriba explicamos operaciones sobre conjuntos abiertos, uno correspondiente a cada conectivo lógico; también hay conjuntos abiertos correspondientes a los símbolos true y false. Exploramos esto en un ejercicio.
Que (X, Op) sea un espacio topológico.
- Supongamos que el símbolo true corresponde a un conjunto abierto tal que para cualquier conjunto abierto U\(\in\) Op, tenemos (true\(\land\) U) = U. ¿Qué set abierto es?
- Otras cosas que debemos esperar de true incluyen (true\(\lor\) U) = true y (U ⇒ true) = true y (true ⇒ U) = U. ¿Estos aguantan para tu respuesta al 1?
- El símbolo false corresponde a un conjunto abierto U\(\in\) Op tal que para cualquier conjunto abierto U\(\in\) Op, tenemos (false\(\lor\) U) = U. ¿Qué set abierto es?
- Otras cosas que debemos esperar de false incluyen (false\(\land\) U) = false y (false ⇒ U) = true. ¿Estos aguantan para tu respuesta al 1? ♦
Para un haz vectorial π: E → X sobre un espacio X, la gavilla correspondiente es Secπ correspondiente a sus secciones: a cada conjunto abierto i\(_{U}\): U\(\subseteq\) X, asociamos el conjunto de funciones s: U → E para el cual s; π = i\(_{U}\). Por ejemplo, en el caso del haz tangente π: T M → M (ver Ejemplo 7.46), la gavilla correspondiente, llamarla VF, asocia a cada U el conjunto VF (U) de campos vectoriales en U.
La lógica interna de los topos se puede utilizar entonces para considerar las propiedades de los campos vectoriales. Por ejemplo, se podría tener un predicado Grad: VF → Ω que pide el subespacio más grande Grad (v) en el que un campo vectorial dado v proviene del gradiente de alguna función escalar. También se podría tener un predicado que pida el conjunto abierto más grande en el que un campo vectorial no sea cero. Las operaciones lógicas como\(\land\) y luego\(\lor\) podrían aplicarse para afinar en subcolectores precisos a lo largo de los cuales se mantienen varias propiedades deseadas, y para razonar lógicamente sobre qué otras propiedades se ven obligadas a mantener allí.
7.4.3 Predicados
En inglés, un predicado es la parte de la oración que viene después del sujeto. Por ejemplo “.. es par” o “.. le gusta el clima” son predicados. No todos los temas tienen sentido para un predicado dado; por ejemplo, la oración “7 es par” puede ser falsa, pero tiene sentido. En contraste, la frase “2.7 es par” realmente no tiene sentido, y “2.7 le gusta el clima” ciertamente no lo hace En informática, podrían decir “A la expresión '2.7 le gusta el tiempo' no escribe check”.
El punto es que cada predicado está asociado a un tipo, es decir, el tipo de sujeto que tiene sentido para ese predicado. Cuando aplicamos un predicado a un sujeto del tipo apropiado, el resultado tiene un valor de verdad: “7 es par” es verdadero o falso. Quizás “A Bob le gusta el clima” es cierto algunos días y falso en otros. De hecho, este valor de verdad podría cambiar por año (mal tiempo este año), por temporada, por hora, etc. En inglés, esperamos que los valores de verdad de las oraciones cambien con el tiempo, que es exactamente la motivación para este capítulo. Estamos trabajando hacia una lógica donde los valores de la verdad cambian con el tiempo.
En un topos\(\mathcal{E}\) = Shv (X, Op), apredicate es un morfismo de gavilla p: S → Ω donde S\(\in\)\(\mathcal{E}\) es una gavilla y Ω\(\in\)\(\mathcal{E}\) es el clasificador subobjeto, la gavilla de valores de verdad. Por Definición 7.35 obtenemos una función p (U): S (U) → Ω (U) para cualquier conjunto abierto U\(\subseteq\) X. En el ejemplo anterior que discutiremos más cuidadosamente en la Sección 7.5, si S es la gavilla de la gente (la gente va y viene con el tiempo), y Bob\(\in\) S (U) es una persona que existe a lo largo de un tiempo U, y p es el predicado “le gusta el clima”, entonces p (Bob) es el conjunto de tiempos durante los cuales a Bob le gusta el clima. Entonces la respuesta a “A Bob le gusta el clima” es algo así como “en veranos sí, y también en abril de 2018 y mayo de 2019 sí, pero en todos los demás tiempos no”. Eso es p (Bob), el valor de verdad temporal obtenido aplicando el predicado p al sujeto Bob.
Justo ahora describimos cómo un predicado p: S → Ω, como “.. le gusta el clima”, actúa sobre las secciones s\(\in\) S (U), digamos s = Bob. Pero por Definición 7.12, cualquier predicado p: S → Ω también define un subobjeto de {S | p}\(\subseteq\) S. Describir las secciones de esta subgavilla. ♦
El poset de subobjectos. Para un topos\(\mathcal{E}\) = Shv (X, Op) y objeto (gavilla) S\(\in\)\(\mathcal{E}\), el conjunto de S-predicados |Ω\(^{E}\) | =\(\mathcal{E}\) (S, Ω) se le da naturalmente la estructura de un poset, que denotamos
(|Ω\(^{S}\) |, ≤\(^{S}\)) (7.63)
Dados dos predicados p, q: S → Ω, decimos que p ≤\(^{S}\) q si el primero implica el segundo. Más precisamente, para cualquier U\(\in\) Op y sección \(\in\)s S (U) obtenemos dos subconjuntos abiertos p (s)\(\subseteq\) U y q (s)\(\subseteq\) U. Decimos que p ≤\(^{S}\) q si p (s)\(\subseteq\) q (s) para todos los U\(\in\) Op y \(\in\)s S (U). A menudo soltamos el superíndice de ≤\(^{S}\) y simplemente escribimos ≤. En la notación lógica formal, uno podría escribir p ≤\(^{S}\) q usando el símbolo, por ejemplo, de una de las siguientes maneras:
s: S | p (s) q (s) o p (s)\(_{s:S}\) q (s).
En particular, si S = 1 es el objeto terminal, denotamos |Ω\(^{S}\) | por |Ω|, y nos referimos a los elementos p\(\in\) |Ω| como proposiciones. Son solo morfismos p: 1 → Ω.
Este preorden se ordena parcialmente un poset que significa que si p ≤ q y q ≤ p entonces p = q.
El motivo es que para cualquier subconjunto U, V\(\subseteq\) X, si U\(\subseteq\) V y V\(\subseteq\) U entonces U = V.
Dé un ejemplo de un espacio X, una gavilla S\(\in\) Shv (X), y dos predicados p, q: S → Ω para los que se mantiene p (s)\(_{s:S}\) q (s).
No hay que ser formal. ♦
Todos los símbolos lógicos (true, false,,\(\land\)\(\lor\), ⇒, ¬) de la Sección 7.4.2 tienen sentido en cualquier poset |Ω\(^{S}\) |.
Para cualquiera de dos predicados p, q: S → Ω, definimos (p\(\land\) q): S → Ω por (p\(\land\) q) (s) := p (s)\(\land\) q (s), y de manera similar para\(\lor\). Así se dice que estas operaciones se computan puntualmente sobre S.
Con estas definiciones, el\(\land\) símbolo es el encuentro y el\(\lor\) símbolo es la unión en el sentido de Definición 1.81 para el poset |Ω\(^{S}\) |.
Con toda la estructura lógica que hemos definido hasta ahora, el poset |Ω\(^{S}\) | de predicados en S forma lo que se llama álgebra Heyting. No lo definiremos aquí, pero se puede encontrar más información en la Sección 7.6. Pasamos ahora a la cuantificación.
7.4.4 Cuantificación
La cuantificación viene en dos sabores: universal y existencial, o 'para todos' y 'existe. ' Cada uno toma un predicado de n + 1 variables y devuelve un predicado de n variables.
Supongamos que tenemos dos poleas S, T\(\in\) Shv (X, Op) y un predicado p: S × T → Ω. Digamos que T representa lo que se considera digno de noticias y S vuelve a ser el conjunto de personas. Entonces, para un subconjunto de tiempo U, una sección t\(\in\) T (U) es algo que se considera de importancia noticiosa a lo largo de toda U, y una sección \(\in\)s S (U) es una persona que dura todo la totalidad de U. Imaginemos el predicado p como “s está preocupado por t”. Ahora recordemos de la Sección 7.4.3 que un predicado p no devuelve simplemente verdadero o falso; dada una persona s y un elemento de noticias t, devuelve un valor de verdad correspondiente al subconjunto de tiempos en los que p (s, t) es verdadero.
“Para todo t en T,.. está preocupado por t” es en sí mismo un predicado sobre una sola variable, S, que denotamos
B (t: T). p (s, t).
Aplicar este predicado a una persona devuelve los tiempos en que esa persona está preocupada por todo en las noticias. De igual manera, “existe t en T tal que s está preocupado por t” también es un predicado sobre S, que denotamos (t: T). p (s, t). Si aplicamos este predicado a una persona s, obtenemos los momentos en que la persona s está preocupada por al menos una cosa en las noticias.
En el conjunto de topos, donde Ω =\(\mathbb{B}\), considere el predicado p:\(\mathbb{N}\) ×\(\mathbb{Z}\) →\(\mathbb{B}\) dado por

1. Cuál es el conjunto de n\(\in\)\(\mathbb{N}\) para el que el predicado p (z:\(\mathbb{Z}\)). p (n, z) sostiene?
2. Cuál es el conjunto de n\(\in\)\(\mathbb{N}\) para el que el predicado (z:\(\mathbb{Z}\)). p (n, z) sostiene?
3. Cuál es el conjunto de z\(\in\)\(\mathbb{Z}\) para el cual el predicado p (n:\(\mathbb{N}\)). p (n, z) sostiene?
4. Cuál es el conjunto de z\(\in\)\(\mathbb{Z}\) para el cual el predicado (n:\(\mathbb{N}\)). p (n, z) sostiene? ♦
Entonces dado p, tenemos un predicado cuantificado universalmente y existencialmente [p] (t: T). p (s, t) y (t: T). p (s, t) sobre S. ¿Cómo los entendemos formalmente como morfismos de gavilla S → Ω o, equivalentemente, como subpoleas de S?
Cuantificación universal. Dado un predicado p: S × T → Ω, el predicado universalmente cuantificado (t: T). p (s, t) toma una sección s\(\in\) S (U), para cualquier conjunto abierto U, y devuelve un cierto conjunto abierto V\(\in\) Ω (U). A saber, devuelve el conjunto abierto más grande V\(\subseteq\) U para el que p (s |\(_{v}\), t) = V se mantiene para todos \(\in\)t T (V).
Supongamos que s es una persona viva durante todo el intervalo U. Aplicar la definición anterior al ejemplo p (s, t) = “persona s está preocupada por las noticias t” del Ejemplo 7.65. Aquí, T (V) es el conjunto de ítems que están en las noticias a lo largo del intervalo V.
- Qué subconjunto abierto de U es [p] (t: T). p (s, t) para una persona s?
- ¿Tiene el significado semántico que esperarías, dada la descripción menos formal en la Sección 7.4.4? ♦
En términos abstractos, el predicado universalmente cuantificado corresponde al subgavillo dado por el siguiente retroceso:
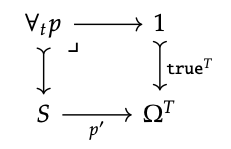
donde p ′: S → Ω\(^{T}\) es el currying de S × T → Ω y true\(^{T}\) es el currying del compuesto 1 ×\(T \stackrel{!}{\rightarrow} A \stackrel{true}{\rightarrow} Ω\).
Ver Eq. (7.10).
Cuantificación existencial. Dado un predicado p: S × T → Ω, el predicado cuantificado existencialmente (t: T). p (s, t) toma una sección s\(\in\) S (U), para cualquier conjunto abierto U, y devuelve un cierto conjunto abierto V\(\in\) Ω (U), es decir, la unión V = \(\bigcup_{i}\) V\(_{i}\) de todos los conjuntos abiertos V i para los que existe algo de ti\(\in\) T (V i) satisfaciendo p (s |\(_{Vi}\), t\(_{i}\)) = V \(_{i}\). Si el resultado es U mismo, podrías estar tentado a pensar “ah, entonces existe algo de t\(\in\) T (U) satisfaciendo p (t)”, pero eso no es necesariamente así. Apenas hay una portada de U =\(\bigcup{U_{i}}\) y secciones locales ti\(\in\) T (U\(_{i}\)), cada una satisfaciendo p, como se explicó anteriormente. Así el cuantificador existencial está haciendo mucho trabajo “bajo el capó”, tomando en cuenta los recubrimientos sin mostrar ese hecho en la notación.
Aplicar la definición anterior al predicado de “persona s está preocupada por noticias t” del Ejemplo 7.65.
1. Qué conjunto abierto es (t: T). p (s, t) para una persona s?
2. ¿Tiene el significado semántico que esperarías? ♦
En términos abstractos, el predicado cuantificado existencialmente se da de la siguiente manera.
Comience con el subobjeto clasificado por p, es decir {(s, t)\(\in\) S × T | p (s, t)}\(\subseteq\) S × T, componer con la proyección π\(_{S}\): S × T → S como en la parte superior derecha; luego tomar la factorización epimono del compuesto como en la parte inferior izquierda:
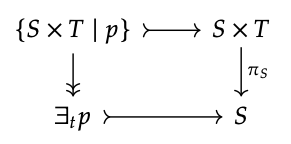
Entonces el mapa inferior es la subgavilla deseada de S.
7.4.5 Modalidades
De vuelta en el Ejemplo 1.123 discutimos operadores modales también conocidos como modalidades diciendo que son operadores de cierre en preordenes que surgen en lógica. Los preordenes a los que nos referíamos son los discutidos en la Ec. (7.63): para cualquier objeto S\(\in\)\(\mathcal{E}\) existe el poset (|Ω\(^{S}\) |, ≤\(^{S}\)) de predicados sobre S, donde |Ω\(^{S}\) | =\(\mathcal{E}\) (S, Ω) es solo el conjunto de morfismos S → Ω en la categoría\(\mathcal{E}\).
Una modalidad en Shv (X) es un morfismo de gavilla j: Ω → Ω que satisface tres propiedades para todos U\(\subseteq\) X y p, q\(\in\) Ω (U):
a) p ≤ j (p);
b) j; j) p) ≤ j (p); y
(c) j (p\(\land\) q) = j (p)\(\land\) j (q).
Supongamos que j: Ω → Ω es un morfismo de poleas en X, tal que p ≤ j (p) se mantiene para todos los U\(\subseteq\) X y p\(\in\) Ω (U). Mostrar que para todos q\(\in\) Ω (U) tenemos j (j (q)) ≤ j (q) iff j (j (q)) = j (q) . ♦
En el Ejemplo 1.123 dijimos informalmente que para cualquier proposición p, por ejemplo “Bob está en San Diego”, hay un operador modal “asumiendo p,...” Ahora estamos en condiciones de hacerlo formal.
Fijar una proposición p\(\in\) |Ω|. Entonces
(a) el morfismo de gavilla Ω → Ω dado al enviar q a p ⇒ q es una modalidad.
(b) el morfismo de gavilla Ω → Ω dado al enviar q a p\(\lor\) q es una modalidad.
(c) el morfismo de gavilla Ω → Ω dado al enviar q a (q ⇒ p) ⇒ p es una modalidad.
No podemos probar aquí la Proposición 7.71, pero damos referencias en la Sección 7.6.
Que S sea la gavilla de la gente como en la Sección 7.4.3, y que j: Ω → Ω sea “asumiendo que Bob está en San Diego...”
- Nombra cualquier predicado p: S → Ω, como “le gusta el clima”.
- Elija un intervalo de tiempo U. Para una persona arbitraria \(\in\)s (U), ¿qué tipo de cosas es p (s), y qué significa?
- ¿Qué tipo de cosas es j (p (s)) y qué significa?
- ¿Es cierto que p (s) ≤ j (p (s))? Explique brevemente.
- ¿Es cierto que j (j (p (s))) = j (p (s)))? Explique brevemente.
- Elija otro predicado q: S → Ω. ¿Es cierto que j (p\(\land\) q) = j (p)\(\land\) j (q)? Explique brevemente. ♦
7.4.6 Teorías de tipo y semántica
Hemos estado hablando de la lógica de un topos en cuanto a sets abiertos, pero en realidad se trata de una combinación de dos ideas que son realmente mejor dejarlas sin conflar. El primero es la lógica, o lenguaje formal, y el segundo es la semántica, o significado. El lenguaje formal se ve así:
B (t: T). (s: S). f (s) = t (7.73)
y las declaraciones semánticas son como “el morfismo de gavilla f: S → T es un epimorfismo”. En el primero, mundo lógico, todas las declaraciones son expresiones lingüísticas formadas de acuerdo con reglas estrictas y todas las pruebas son deducciones que también siguen reglas estrictas. En este último, el mundo semántico, las declaraciones y las pruebas son sobre las propias gavillas, como objetos matemáticos. Admitimos que se trata de declaraciones toscas; de nuevo, nuestro objetivo aquí es sólo dar un sabor, una invitación a una lectura más profunda.
Proporcionar semántica para un sistema lógico significa proporcionar un compilador que convierta cada declaración lógica en el lenguaje formal en una declaración matemática sobre poleas particulares y sus relaciones. Una computadora puede llevar a cabo deducciones lógicas sin saber lo que alguna de ellas “quiere decir” de las poletas. Decimos que la semántica es sólida si toda prueba formal se convierte en un hecho verdadero sobre las poleas relevantes.
A cada topos se le puede asignar un lenguaje formal, a menudo llamado su lenguaje interno, en el que llevar a cabo construcciones y pruebas formales. Este lenguaje tiene una semántica sonora, una especie de compilador de lógica a gavilla que va bajo el nombre de semántica categórica o semántica de Kripke-Joyal. Damos las ideas básicas en la Sección 7.4; damos referencias a la literatura en la Sección 7.6.
En cada topos E, y por cada f: S → T en E, el morfismo f es un epimorfismo si y solo si se sostiene la Ec. (7.73). Por ejemplo, considere el caso de instancias de base de datos en un esquema C, digamos con 100 tablas (una de las cuales podría denotarse c\(\in\) Ob (C)) y 500 columnas de clave externa (una de las cuales podría denotarse f: c → c ′ en C); ver Eq. (3.2).
Si S y T son dos instancias y f es una transformación natural entre ellas, entonces podemos preguntarnos si la Eq. (7.73) sostiene o no. Esta sencilla fórmula es compilada por la semántica de Kripke-Joyal para preguntar:
¿Es cierto que por cada tabla c\(\in\) Ob (C) y cada fila \(\in\)s S (c) existe una fila t\(\in\) T (c) tal que f (s) = t?
Esto es exactamente lo que significa que f sea suryectiva. Quizás esto no sea demasiado impresionante, pero ya sea que se esté hablando de bases de datos o espacios topológicos, o ideas complejas a partir de geometría algebraica, la Ec. (7.73) siempre compila en la cuestión de la surjectividad. Para los espacios topológicos diría algo así como:
¿Es cierto que por cada conjunto abierto U\(\subseteq\) X y cada sección \(\in\)s S (U) del paquete S, existe una cubierta abierta de (U\(_{i}\) \(\subseteq\)U)\(_{i \in I}\) de U y una sección t\(_{i}\) \(\in\)T (U\(_{i}\)) del haz T para cada i\(\in\) I, tal que f (t\(_{i}\)) = s |\(_{U_{i}}\) es la restricción de s a U\(_{i}\)?


