7.3: Polea

Última actualización
Guardar como PDF

Page ID: 112353

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La teoría de la gavilla comenzó antes que la teoría de categorías, por ejemplo, en forma de algo llamado “sistemas de coeficientes locales para grupos de homología”. Sin embargo, su formulación moderna en términos de funtores y sitios se debe a Grothendieck, quien también inventó toposes.

La idea básica es que más que estudiar los espacios, debemos estudiar lo que sucede en los espacios. Un espacio no es más que el 'sitio' en el que suceden las cosas. Por ejemplo, si pensamos en el plano$\mathbb{R^{2}}$ como un espacio, podríamos examinar sólo puntos y regiones en él. Pero si pensamos en un sitio donde suceden las cosas, entonces podríamos pensar en cosas como sistemas meteorológicos en todo el plano, o dunas de arena, o trayectorias y flujos de material.$\mathbb{R^{2}}$ Hay muchas clases de cosas que pueden suceder en un espacio, y estas son las gavillas: una gavilla en un espacio es más o menos “una especie de cosa que puede suceder en el espacio”. Si queremos pensar en puntos o regiones desde la perspectiva de la gavilla, los consideraríamos como diferentes puntos de vista sobre lo que está sucediendo. Es decir, se trata de lo que sucede en un espacio: las partes del espacio son solo perspectivas desde las que ver el programa.

Esto es una reminiscencia de bases de datos. El esquema de una base de datos no es la parte interesante; los datos son lo interesante. Para ser claros, el esquema de una base de datos es un sitio que está actuando como el espacio y la categoría de todas las instancias en ella es un topos. En general, podemos pensar en cualquier pequeña categoría C como un sitio; los topos correspondientes es la categoría de funtores C$^{op}$ → Conjunto. $^{5}$Tales funtores se llaman preheaves en C.

¿Te diste cuenta de que acabamos de introducir una enorme clase de toposes? Para cualquier categoría C, dijimos que hay un topos de presheaves en ella. Entonces, antes de pasar a las polainas, discutamos este tema preliminar de los presheaves. Empezaremos a desarrollar alguna terminología y formas de pensar que posteriormente se generalizarán a poletas.

Preheaves

Recordemos la definición de funtor y transformación natural de la Sección 3.3. Los presheaves son solo funtores, pero tienen una terminología especial que nos lleva a pensar en ellos de cierta manera geométrica.

Definición 7.22.

Que C sea una categoría pequeña. Un preheaf P en C es un functor P: C$^{op}$ → Set. A cada objeto c$\in$ C, nos referimos al conjunto P (c) como el conjunto de secciones de P sobre c. A cada morfismo f: c ′ → c, nos referimos a la función P (f): P (c) → P (c ′) como el mapa de restricción a lo largo de f. Para cualquier sección s$\in$ P (c), podemos denotar P (f) (s)$\in$ P (c ′), es decir, su restricción a lo largo de f, por s|$_{f}$.

Si P y Q son pre-heaves, un morfismo α: P → Q entre ellos es una transformación natural de los funtores

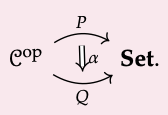
$Screen Shot 2021-01-25 a las 5.24.29 PM.png$

Ejemplo 7.23.

Deje que ArsHP sea la categoría que se muestra a continuación:

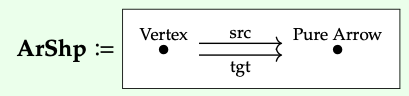
$Screen Shot 2021-01-25 a las 5.31.15 PM.png$

La razón por la que llamamos a nuestra categoría ARSHP es que podemos imaginarla como una 'forma de flecha'.

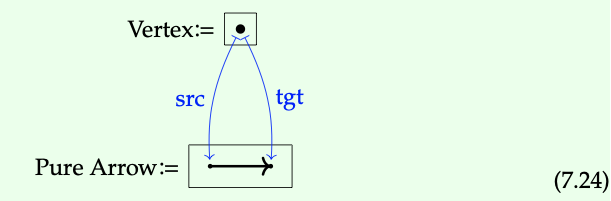
$Screen Shot 2021-01-25 at 5.31.48 PM.png$

Un presheaf en ArsHP es un functor I: ARSHP$^{op}$ → Set, que es una instancia de base de datos en ARSHP$^{op}$. Tenga en cuenta que ArsHP$^{op}$ es lo que llamamos Gr en la Sección 3.3.5; ahí demostramos que las instancias de base de datos en Gr —es decir, pre-heaves en ArsHP — son solo gráficas dirigidas, e.g.

$Screen Shot 2021-01-25 at 5.32.26 PM.png$

Pensando en presheaves en cualquier categoría C, a menudo tiene sentido imaginar los objetos de C como formas de algún tipo, y los morfismos de C como mapas continuos entre formas, tal como hicimos para la forma de flecha en la Ec. (7.24). En ese contexto, uno puede pensar en un presheaf P como una especie de construcción lego: P se construye a partir de las formas en C, conectadas entre sí usando los morfismos en C. En el caso en que C es la forma de flecha, un presheaf es una gráfica. Entonces esto diría que una gráfica es una especie de construcción lego, construida a partir de vértices y flechas conectadas entre sí utilizando la inclusión de un vértice como fuente u objetivo de una flecha. ¿Lo puedes ver?

Esta afirmación puede hacerse bastante precisa; aunque no podemos pasar por ello aquí, la idea de lego anterior se resume con la declaración formal de que “la categoría de presheaves en C es la finalización libre de colimit de C.” Pregunta a un amable teórico de la categoría de barrio para más detalles.

Sin embargo, uno piensa en pre-heaves en términos de ensamblajes lego o instancias de bases de datos, son relativamente sencillos. La diferencia entre preheaves y poleas es que las poleas toman en cuenta algún tipo de 'información de cubierta'. La noción trivial de cubrir es decir que cada objeto se cubre a sí mismo y nada más; si uno usa esta cobertura trivial, las prehebas y las poleas son lo mismo. En nuestro contexto conductual necesitaremos una noción no trivial de cobertura, por lo que las poleas y las preheaves serán ligeramente diferentes. Nuestro siguiente objetivo es entender las poletas en un espacio topológico.

Espacios Topológicos

Decíamos en la Sección 7.3 que, más que los espacios de estudio, consideramos los espacios como meros 'sitios' en los que suceden las cosas. También dijimos que las cosas que pueden pasar en un espacio se llaman poleas, y siempre forman un tipo de categoría llamada topos. Para definir un topos de poletas, debemos comenzar por el sitio en el que existen.

Los sitios son objetos matemáticos muy abstractos, y no los haremos precisos en este libro. Sin embargo, uno de los tipos de sitios más fáciles de pensar son los que provienen de espacios topológicos: cada espacio topológico tiene naturalmente la estructura de un sitio. Hemos hablado de espacios por un tiempo sin hacerlos precisos; hagámoslo ahora.

Definición 7.25.

Que X sea un conjunto, y dejemos que$P(X) = \{U \subseteq X\} denote its set of subsets. A topology on X is a subset Op \(\subseteq$ P (X), elementos de los cuales llamamos conjuntos abiertos,$^{6}$ satisfaciendo las siguientes condiciones:

Conjunto completo: el subconjunto X$\subseteq$ X está abierto, es decir, X$\in$ Op.
Intersecciones binarias: si U, V$\in$ Op entonces (U V)$\in$ Op.
Sindicatos arbitrarios: si yo es un conjunto y si se nos da un conjunto abierto Ui$\in$ Op para cada i, entonces su unión también está abierta, ($\bigcup_{i \in I} U_{i}$$\in$Op. Interpretamos el caso particular donde I = Ø significa que el conjunto vacío está abierto: Ø$\in$ Op.

Si$U = \bigcup_{i \in I} U_{i}$, decimos que (U i)$_{i \in I}$ cubre U.

Un par (X, Op), donde X es un conjunto y Op es una topología en X, se denomina espacio topológico.

Una función continua entre los espacios topológicos (X, Op$_{X}$) y (Y, Op$_{Y}$) es una función f: X → Y tal que por cada U$\in$ Op$_{Y}$, el preimagen f$^{−1}$ (U) está en Op$_{X}$.

Al final de la Sección 7.3.1 mencionamos en qué se diferencian las poleas de las preheaves en que toman en cuenta 'información de cobertura'. La noción de cubrir un conjunto abierto por una unión de otros conjuntos abiertos se definió en la Definición 7.25, y entrará en juego cuando definamos poleas en la Definición 7.35.

Ejemplo$\PageIndex{1}$

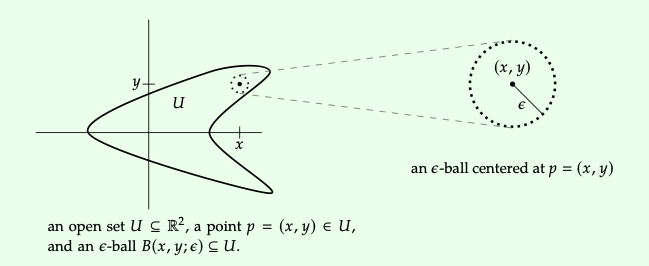
La topología habitual Op sobre R2 se basa en 'ε-balls.' Para cualquier ε$\in$$\mathbb{R}$ con ε > 0, y cualquier punto p = (x, y)$\in$$\mathbb{R^{2}}$, defina la ε -ball centrada en p para que sea:

$B(p ; \epsilon):=\left\{p^{\prime} \in \mathbb{R}^{2} \mid d\left(p, p^{\prime}\right)<\epsilon\right\}^{7}$

En otras palabras, B (x, y; ε) es el conjunto de todos los puntos dentro de ε de (x, y).

Para un subconjunto arbitrario U $\subseteq$$\mathbb{R^{2}}$, lo llamamos abierto y lo ponemos en Op si,

por cada (x, y)$\in$ U existe un (suficientemente pequeño) ε > 0 tal que B (x, y; ε)$\subseteq$ U.

$Screen Shot 2021-01-26 a las 7.10.07 PM.png$

La misma idea funciona si$\mathbb{R^{2}}$ reemplazamos por cualquier otro espacio métrico X (Definición 2.51): puede considerarse como un espacio topológico donde los conjuntos abiertos son subconjuntos U tal que para cualquier p$\in$ U hay una ε-ball centrada en p y contenida en U. Así que cada espacio métrico puede ser considerado como un espacio topológico.

Ejercicio 7.27.

Considera el conjunto$\mathbb{R}$. Es un espacio métrico con d (x$_{1}$, x$_{2}$) := | x$_{1}$ − x$_{2}$ |.

1. ¿Cuál es el análogo unidimensional de las bolas ε-como se encuentra en el Ejemplo 7.26? Es decir, para cada x$\in$$\mathbb{R}$, defina B (x, ε).

2. ¿Cuándo se$\subseteq$$\mathbb{R}$ llama abierto un subconjunto arbitrario U, en analogía con el Ejemplo 7.26?

3. Encuentra tres conjuntos abiertos U$_{1}$$_{2}$, U y U en$\mathbb{R}$, tal que$\bigcup_{i \in {1,2}}$ cubra U.

4. Encuentra un set abierto U y una colección$\bigcup_{i \in I}$ de sets abiertos donde yo sea infinito, tal que$\bigcup_{i \in I}$ cubra U. ♦

Ejemplo 7.28.

Para cualquier conjunto X, hay una topología 'más gruesa', teniendo el menor número posible de conjuntos abiertos: Op$_{crse}$ = (Ø, X). También hay una topología 'más fina', que tiene tantos conjuntos abiertos como sea posible: Op$_{fine}$ = P (X). Este último, (X, P (X)) se llama el espacio discreto en el conjunto X.

Ejercicio 7.29.

1. Verificar que para cualquier conjunto X, lo que llamamos Op$_{crse}$ en el Ejemplo 7.28 realmente es una topología, es decir, satisface las condiciones de la Definición 7.25.

2. Verificar también que Op$_{fine}$ realmente sea una topología.

3. Mostrar que si (X, P (X)) es discreto y (Y, Op$_{Y}$) es cualquier espacio topológico, entonces cada función X → Y es continua. ♦

Ejemplo 7.30.

Hay cuatro topologías posibles en X = {1, 2}. Dos son Op crse y Op fine del Ejemplo 7.28. Los otros dos son:

Op$_{1}$ := {Ø, {1}, X} y Op$_{2}$ := {Ø, {2}, X}

Los dos espacios topológicos ({1, 2}, Op$_{1}$) y ({1, 2}, Op$_{2}$) son isomórficos; cualquiera de ellos puede llamarse el espacio Sierpinski.

Los conjuntos abiertos de un espacio topológico forman un preorden. Dado un espacio topológico (X, Op), el conjunto Op tiene la estructura de un preorden usando la relación de subconjunto, (Op,$\subseteq$). Es reflexivo porque U (\ subseteq\) U para cualquier U$\in$ Op, y es transitivo porque si U (\ subseteq\) V y V (\ subseteq\) W entonces U (\ subseteq\) W.

Recordemos de la Sección 3.2.3 que podemos considerar cualquier preorden, y por lo tanto Op, como una categoría: sus objetos son los conjuntos abiertos U y para cualquier U, V el conjunto de morfismos Op (U, V) está vacío si U (\ notsubseteq\) V y tiene un elemento si U (\ subseteq\) V.

Ejercicio 7.31.

Recordemos el espacio Sierpinski, digamos (X, Op$_{1}$) del Ejemplo 7.30.

1. Anote el diagrama de Hasse para su preorden de abiertos.
2. Anota todas las portadas.

Ejercicio 7.32.

Dado cualquier espacio topológico (X, Op), a cualquier subconjunto Y (\ subseteq\) X se le puede dar la topología subespacial, llamarlo Op$_{?∩Y}$.

Esta topología define cualquier A (\ subseteq\) Y para que esté abierta, A$\in$ Op? Y, si hay un conjunto abierto B$\in$ Op tal que A = B Y.

1. Encuentra una$\in$ Op B que demuestre que todo el conjunto Y está abierto, es decir, Y$\in$ Op$_{?∩Y}$.

2. Mostrar que Op$_{?∩Y}$ es una topología en el sentido de Definición 7.25. $^{8}$

3. Mostrar que la función de inclusión Y → X es una función continua. ♦

OBSERVACIÓN 7.33. Supongamos que (X, Op) es un espacio topológico, y considera el preorden (Op, (\ subseteq\)) de los conjuntos abiertos. Resulta que (Op, (\ subseteq\), X,) es siempre una quantale en el sentido de la Definición 2.79. No vamos a necesitar este hecho, pero invitamos al lector a pensarlo un poco en el Ejercicio 7.34.

Ejercicio 7.34.

En las Secciones 2.3.2 y 2.3.3 discutimos cómo las categorías Bool son pre- órdenes y las categorías Costo son espacios métricos Lawvere, y en la Sección 2.3.4 imaginamos interpretaciones de categorías V para otros cuantales V.

Si (X, Op) es un espacio topológico y V la quantale correspondiente como en Remark 7.33, ¿cómo podríamos imaginar una categoría V? ♦

Polea sobre espacios topológicos

Para resumir dónde estamos, un espacio topológico (X, Op) es un conjunto X junto con un montón de subconjuntos que llamamos 'abierto'; estos subconjuntos abiertos forman un preorden y por lo tanto categoría denotada Op. Las poleas en X serán preheaves en Op con una propiedad especial, acertadamente llamada “condición de gavilla”.

Recordemos la terminología y notación para presheaves: un presheaf en Op es un functor P: Op$^{op}$ → Set. Así, a cada conjunto abierto U$\in$ Op tenemos un conjunto P (U), llamado el conjunto de secciones sobre U, y a cada inclusión de conjuntos abiertos V (\ subseteq\) U tenemos una función P (U ) → P (V) llama la restricción. Si s$\in$ P (U) es una sección sobre U, podemos denotar su restricción a V por s |$_{V}$. Recordemos que decimos que una colección de conjuntos abiertos$\left(U_{i}\right)_{i \in I}$ cubre un conjunto abierto U si U =$\bigcup_{i \in\ I} U_{i}$.

Ahora estamos listos para dar la siguiente definición, que viene en varias ondas: primero definimos familias coincidentes, luego pegando, luego condición de gavilla, luego gavilla, y finalmente la categoría de gavillas.

Definición 7.35.

Que (X, Op) sea un espacio topológico, y que P: Op$^{op}$ → Set sea un presheaf en Op.

Dejar$\left(U_{i}\right)_{i \in I}$ ser una colección de conjuntos abiertos U$_{i}$$\in$ Op cubriendo U.

Una familia coincidente (s i)$_{i \in\I}$ de P-secciones sobre$\bigcup{i}_{i \in\ I}$ consiste en una sección si$\in$ P (U i) para cada i$\in$ yo, tal que por cada i, j$\in$ yo tenemos

$\left.s_{i}\right|_{u_{i} \cap u_{j}}=\left.s_{j}\right|_{U_{i} \cap u_{j}}$

Dada una familia coincidente$si_{i \in\ I}$ para la portada U =$\bigcup_{i \in\ I} U_{i}$, decimos que s$\in$ P (U) es una sección pegada, o pegada, de la familia coincidente si s |$_{Ui}$ = si se sostiene para todos i $\in$Yo. Si existe un encolado único s$\in$ P (U) para cada familia coincidente$si_{i \in\ I}$, decimos que P satisface la condición de gavilla para la cubierta U =$\bigcup_{i \in\ I} U_{i}$. Si P satisface la condición de gavilla para cada cobertura, decimos que P es una gavilla encendida (X, Op).

Por lo tanto, una gavilla es solo un prefajo que satisface la condición de gavilla para cada cubierta abierta.

Si P y Q son gavillas, entonces un morfismo f: P → Q entre estas gavillas no es más que un morfismo es decir, una transformación natural entre sus presheaves subyacentes. Denotamos por Shv (X, Op) la categoría de poleas en X.

La categoría de poleas en X es un topos, pero ya llegaremos a eso.

Ejemplo 7.36.

Aquí hay un caso especial divertido pero muy importante al que se aplica la noción de familia coincidente. No damos este ejemplo por intuición, sino porque (para enfatizar) es un caso importante y fácil de pasar por alto. Al igual que la suma de no números es 0 y el producto de no números es 1, la unión de no conjuntos es el conjunto vacío. Así, si tomamos U = Ø$\subseteq$ X e I = Ø, entonces la colección vacía de subconjuntos (uno por cada i$\in$ I, de los cuales no hay ninguno) cubre U. En este caso la tupla vacía () cuenta una familia coincidente de secciones, y es la única familia coincidente para la cubierta vacía del conjunto vacío.

Es decir, para que un presheaf P: Op$^{op}$ → Set sea una gavilla, una condición necesaria (pero rara vez suficiente) es que P (Ø)$\cong$ {()}, es decir, P (Ø) debe ser un conjunto con un elemento.

Ejemplo extendido: secciones de una función. Este ejemplo es para la intuición, y da un caso donde la terminología de 'sección' y 'restricción' son fáciles de visualizar. Considera la función f: X → Y que se muestra a continuación, donde cada elemento de X se envía al elemento de Y inmediatamente debajo de él.

Por ejemplo, f (a$\_{1}$) = f (a$\_{2}$) = a, f (b$\_{1}$) = b, y así sucesivamente.

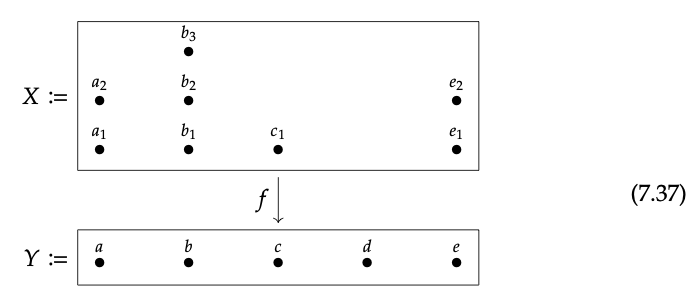
$Screen Shot 2021-01-26 a las 7.44.06 PM.png$

Para cada punto y$\in$ Y, el conjunto de preimagen f$^{−1}$ (y)$\subseteq$ X por encima de él a menudo se llama la fibra sobre y. Tenga en cuenta que diferentes f organizarían los ocho elementos de X de manera diferente sobre Y: los elementos de Y tendrían diferentes fibras.

Ejercicio 7.38.

Considera la función f: X → Y mostrada en la Ec. (7.37).

¿Cuál es la fibra de f sobre a?
¿Cuál es la fibra de f sobre c?
¿Cuál es la fibra de f sobre d?
Dio un ejemplo de una función f ′: X → Y para la cual cada fibra tiene uno o dos elementos. ♦

Consideremos X e Y como espacios topológicos discretos, por lo que cada subconjunto está abierto y f es automáticamente continuo (ver Ejercicio 7.29). Pensaremos en f como un arreglo de X sobre Y, en términos de fibras como el anterior, y lo usaremos para construir una gavilla sobre Y. Para ello, comenzamos por construir un prefundido, es decir, un funtor Sec f: Op (Y)$^{op}$ → Set y luego probaremos que es una gavilla.

Defina la Sec presheaf$_{f}$ en un subconjunto arbitrario U$\subseteq$ Y por:

$\operatorname{Sec}_{f}(U):=\{s: U \rightarrow X \mid(s \text { ; } f)(u)=u \text { for all } u \in U\}$

Se podría describir Sec$_{f}$ (U) como el conjunto de todas las formas de elegir una 'sección transversal' de la disposición f sobre U. Es decir, un elemento s$\in$ Sec$_{f}$ (U) es una elección de un elemento por fibra sobre U. Como ejemplo, digamos U = {a, b}. ¿Cuántas de esas s hay en Sec$_{f}$ (U)? Para responder a esto, recortemos la imagen (7.37) y veamos solo la parte relevante:

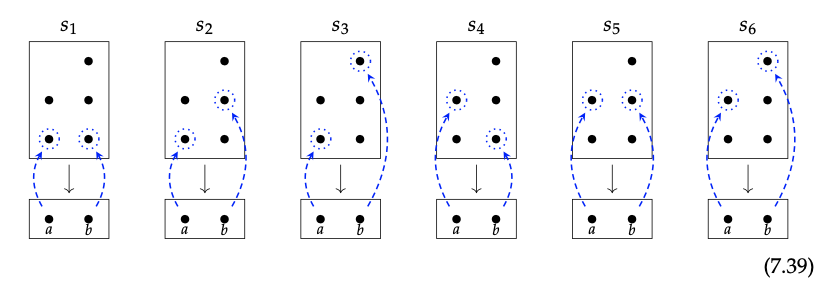
$Screen Shot 2021-01-28 en 1.41.18 PM.png$

Mirando la imagen (7.39), ¿ves cómo obtenemos todas las secciones transversales de f sobre U?

Ejercicio 7.40.

Consulte la Ec. (7.37).

Dejar V$_{1}$ = {a, b, c}. Dibuja todas las secciones sobre él, es decir, todos los elementos de la Sec$_{f}$ (V$_{1}$), como hicimos en la Ec. (7.39).
Dejar V$_{2}$ = {a, b, c, d}. Nuevamente dibuja todas las secciones, Sec$_{f}$ (V$_{2}$).
Sea V$_{3}$ = {a, b, d, e}. ¿Cuántas secciones (elementos de Sec$_{f}$ (V$_{3}$)) hay? ♦

A estas alturas ya deberías entender las secciones de Sec f (U) para diversas U$\subseteq$ X. Esto es Sec$_{f}$ en los objetos, así que estás a mitad de camino de entender a la Sec$_{f}$ como un presheaf. Es decir, como presheaf, Sec$_{f}$ también incluye mapas de restricción para cada subconjunto V$\subseteq$ U.

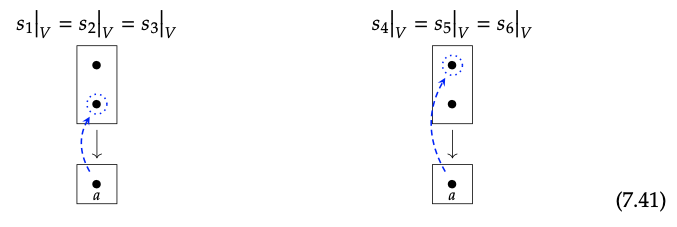
Por suerte, los mapas de restricción son fáciles: si V$\subseteq$ U, digamos V = {a} y U = {a, b}, luego dada una sección s como en la Ec. (7.39), obtenemos una sección sobre V al 'restringir' nuestra atención a lo que s hace en {a}.

$Screen Shot 2021-01-28 at 1.56.17 PM.png$

Ejercicio 7.42.

Escriba los conjuntos de secciones Sec$_{f}$ ({a, b, c}) y Sec$_{f}$ ({a, c}).
Dibuja líneas de la primera a la segunda para indicar el mapa de restricción.

Ahora hemos entendido a la Sec$_{f}$ como un presheaf; a continuación explicamos cómo ver que se trata de una gavilla, es decir, que satisface la condición de gavilla para cada cobertura. Para entender la condición de gavilla, considere el conjunto U$_{1}$ = {a, b} y U$_{2}$ = {b, e}. Estos cubren el conjunto U = {a, b, e} = U$_{1}$$\bigcup$ U$_{2}$. Por Definición 7.35, una familia coincidente para esta cobertura consiste en una sección sobre U$_{1}$ y una sección sobre U$_{2}$ que coinciden en el conjunto de superposición, $_{1}$U U$_{2}$ = {b}.

Así que considere s$_{1}$$\in$ Sec f (U$_{1}$) y s$_{2}$$\in$ Sec$_{f}$ (U$_{2}$) que se muestran a continuación.

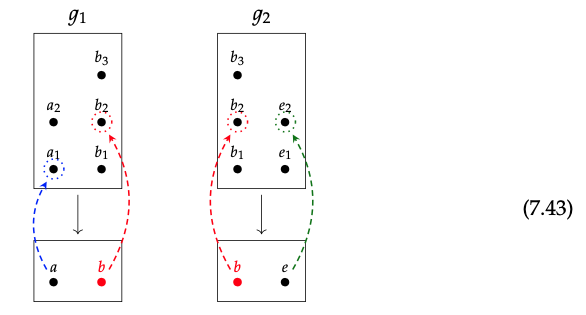
$Screen Shot 2021-01-28 at 1.58.10 PM.png$

Dado que las secciones g$_{1}$ y g$_{2}$ coinciden en la superposición, ambas envían b a b$_{2}$ las dos secciones 122 mostradas en la Ec. (7.43) se pueden pegar para formar una sola sección sobre U = {a, b, e}:

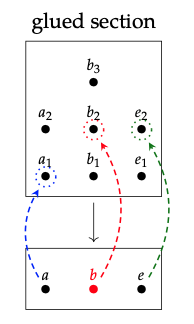
$Screen Shot 2021-01-28 a las 2.04.25 PM.png$

Ejercicio 7.44.

Nuevamente vamos a dejar U$_{1}$ = {a, b} y U$_{2}$ = {b, e}, por lo que el solapamiento$_{1}$ es U U$_{2}$ = {b}.

Encuentra una sección s$_{1}$$\in$ Sec$_{f}$ (U$_{1}$) y una sección s$_{2}$$\in$ Sec$_{f}$ (U$_{2}$) que no estén de acuerdo en la superposición.
Para su (s$_{1}$, s$_{2}$) respuesta (s) en la parte 1, ¿puede encontrar una sección s$\in$ Sec$_{f}$ ($_{1}$$\bigcup$U U$_{2}$) tal que s |$_{U_{1}}$ = s$_{1}$ y s| (_ {U_ {2}}\) = s$_{2}$?
Encuentra una sección h$_{1}$$\in$ Sec$_{f}$ (U$_{1}$) y una sección h$_{2}$$\in$ Sec$_{f}$ (U$_{2}$) que sí coincidan en la superposición, pero que son diferentes a nuestra elección en la Ec. (7.43).
¿Se puede encontrar una sección h$\in$ Sec$_{f}$ ($_{1}$$\bigcup$U U$_{2}$) tal que h |$_{U_{1}}$ = h$_{1}$ y h |$_{U_{2}}$ = h$_{2}$? ♦

Otros ejemplos de poleas. El ejemplo extendido anterior generaliza a cualquier función continua f: X → Y entre espacios topológicos.

Ejemplo 7.45.

Sea f: (X, Op$_{X}$) → (Y, Op$_{Y}$) una función continua. Considere el functor op$\mathrm{Sec}_{f}: \mathrm{Op}_{Y}^{\mathrm{op}} \rightarrow \text { Set }$ → Conjunto dado por

Sec$_{f}$ (U) := {g: U → X | g es continuo y (g; f) (u) = u para todos los u$\in$ U},

Los morfismos de Op$_{Y}$ son inclusiones V$\subseteq$ U. Dado g: U → X y V$\subseteq$ U, lo que llamamos la restricción de g a V es lo habitual que queremos decir con restricción, lo mismo que lo fue en la Ec. (7.41). De nuevo se puede comprobar que la Sec$_{f}$ es una gavilla.

Ejemplo 7.46.

Un buen ejemplo de gavilla en un espacio M es el de los campos vectoriales en M. Si calculas la velocidad del viento en cada punto de la Tierra, tendrás lo que se llama un campo vectorial en la Tierra. Si conoces la velocidad del viento en cada punto de Afganistán y yo conozco la velocidad del viento en cada punto de Pakistán, y nuestros cálculos coinciden alrededor de la frontera, entonces podemos unir nuestra información para obtener la velocidad del viento sobre la unión de los dos países. Todos los posibles campos de velocidad del viento sobre todos los conjuntos abiertos posibles de la superficie de la Tierra forman juntos la gavilla de campos vectoriales.

Digamos esto un poco más formalmente. Un múltiple M solo puedes imaginar una esfera como la superficie de la Tierra siempre tiene algo llamado haz tangente. Se trata de un espacio TM cuyos puntos son pares (m, v), donde m$\in$ M es un punto en el colector y v es un vector tangente que emana de él. Aquí hay una imagen de un plano tangente todos los vectores tangentes que emanan de algún punto fijo en una esfera:

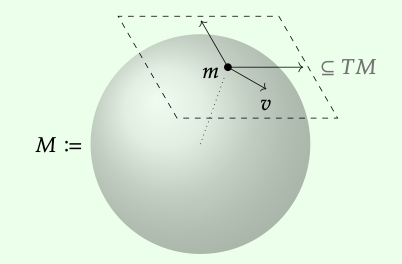
$Screen Shot 2021-01-28 en 2.50.15 PM.png$

El haz tangente TM incluye todo el plano tangente mostrado arriba incluyendo los tres vectores dibujados en él, así como el plano tangente en cualquier otro punto de la esfera.

El haz tangente TM en un colector M viene con un mapa continuo π: TM → M de regreso al colector, enviando (m, v)$\longmapsto$ m. Se podría decir que π “olvida el vector tangente y simplemente recuerda el punto del que emanó”. Por Ejemplo 7.45, π define una gavilla Sec$_{pi}$. Podría llamarse la gavilla de 'secciones vectoriales tangentes en M', pero su nombre habitual es la gavilla de campos vectoriales en M. Esto es lo que estábamos describiendo cuando hablamos de la gavilla de velocidades del viento en la Tierra, arriba. Dado un subconjunto abierto U M, un elemento v$\in$ Sec$_{pi}$ (U) se llama campo vectorial sobre U porque asigna continuamente un vector tangente v (u) a cada punto u$\in$ U. El vector tangente en u nos dice la velocidad del viento en ese punto.

Aquí hay una digresión divertida: en el caso de un colector esférico M como la Tierra, es posible demostrar que por cada conjunto abierto U, siempre y cuando U$\neq$ M, hay un campo vectorial v$\in$ Sec$_{pi}$ (U) que nunca es 0: el viento podría estar soplando a lo largo de U. No obstante, un teorema de Poincaré dice que si miras toda la esfera, se garantiza que habrá un punto m$\in$ M en el que el viento no sopla en absoluto. Es como el ojo de un huracán o quizás un cowlick. Un cowlick en el cabello de alguien ocurre cuando el cabello no tiene dirección para ir, ¡así que se pega! El pelo que se pega no contaría como un vector tangente: los vectores tangentes deben comenzar acostados a lo largo de la cabeza. Poincaré demostró que si tu cabeza estuviera completamente cubierta con el pelo de una pulgada de largo, habría al menos un cowlick. Esta diferencia entre las secciones locales (sobre U$\subseteq$ X arbitrarias) y las secciones globales (sobre X) es decir, que el cabello puede peinarse bien cuando U$\neq$ X pero no puede peinarse bien cuando U = X puede ser pensado como un efecto generativo, y puede medirse por cohomología (ver Sección 1.5).

Ejercicio 7.47.

Si M es una esfera como en el Ejemplo 7.46, sabemos por la Definición 7.35 que podemos considerar la categoría Shv (M) de polainas sobre M; de hecho, tales categorías son toposes y estas son a lo que estamos llegando.

Pero, ¿son las polainas en M los campos vectoriales? Es decir, ¿existe una correspondencia uno a uno entre las poleas en M y las poleas vectoriales en M y los campos vectoriales en M? Si es así, ¿por qué? Si no, ¿cómo se relacionan las poleasen M y los campos vectoriales en M? ♦

Ejemplo 7.48.

Por cada espacio topológico (X, Op), tenemos los topos de gavillas sobre él. Los topos de conjuntos, que se puede considerar como la historia de la teoría de conjuntos, es la categoría de poleas en el espacio de un punto {∗}. En teoría de topos, vemos la categoría de conjuntos una categoría enorme, increíble y rica como correspondiente a un solo punto. Imagínese lo mucho más complejas que son las toposis arbitrarias, cuando pueden tener lugar en espacios topológicos mucho más interesantes (y de hecho 'sitios' aún más generales).

Ejercicio 7.49.

Consideremos el espacio Sierpinski ({1,2}, Op$_{1}$) del Ejemplo 7.30.

¿Cuál es la categoría Op para este espacio? (Es posible que ya lo hayas descubierto en el Ejercicio 7.31; si no, hazlo ahora.)
¿En qué consiste un presheaf on Op?
¿Cuál es la condición de la gavilla para Op?
¿Cómo identificamos una gavilla en Op con una función? ♦

Search