8.1: Soluciones para el Capítulo 1

Última actualización
Guardar como PDF

Page ID: 112233

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ejercicio 1.1

Para cada una de las siguientes propiedades, necesitamos encontrar una función f:$\mathbb{R}$ →$\mathbb{R}$ que la conserve, y otra función la llame que no.
conservación de orden: Tomar f (x) = x + 5; si x ≤ y entonces x + 5 ≤ y + 5, así que f es conservadora de orden.

Tome g (x) := − x; aunque 1 ≤ 2, la desigualdad requerida −1 ≤$^{?}$ −2 no se mantiene, por lo que g no conserva el orden.

métrico-preservativo: Tomar f (x) := x + 5; para cualquier x, y tenemos | x − y | = | (x + 5) − (y + 5) | por las reglas de la aritmética, entonces | x − y | = | f (x) − f (y) |, es decir, f conserva métrica. Toma g (x) := 2 ∗ x; luego con x = 1 e y = 2 tenemos | x − y | = 1 pero |2 x − 2 y | = 2, por lo que g no conserva la métrica.

adicional-conservando: Tomar f (x) := 3 ∗ x; para cualquier x, y tenemos 3 ∗ (x + y) = (3 ∗ x) + (3 ∗ y), así que f conserva adición.

Tomar g (x) := x + 1; luego con x = 0 e y = 0, tenemos g (x + y) = 1, pero g (x) + g (y) = 2, por lo que g no conserva la adición.

Ejercicio 1.4

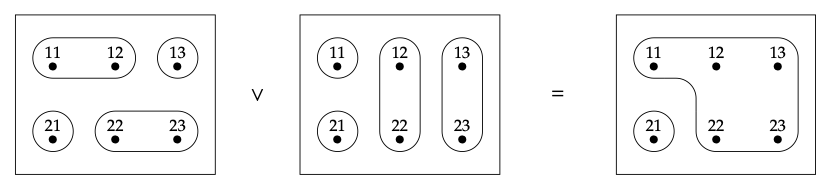
Aquí está la unión de los dos sistemas:

$Screen Shot 2021-02-02 a las 12.48.35 PM.png$

Ejercicio 1.6

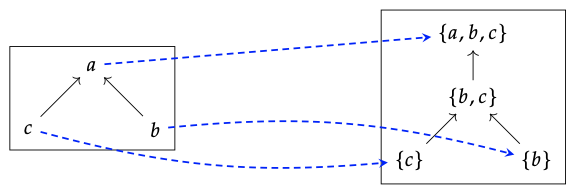
1. Aquí está el diagrama de Hasse para particiones del conjunto de dos elementos {•, ∗}:

$Screen Shot 2021-02-02 a las 12.49.34 PM.png$

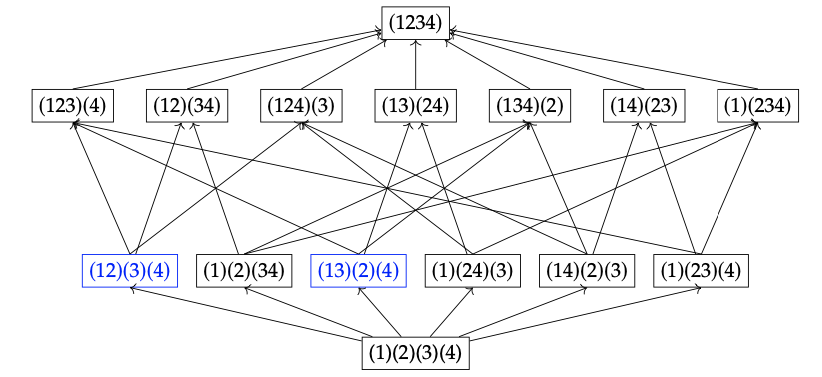
2. Aquí hay una imagen (usando texto, en lugar de círculos) para particiones del conjunto 1, 2, 3, 4:

$Screen Shot 2021-02-02 a las 12.55.29 PM.png$

Para las partes restantes, elegimos A = (12) (3) (4) y B = (13) (2) (4).

3. A$\land$ B = (123) (4).

4. Sí, es cierto que A ≤ (A$\lor$ B) y que B ≤ (A$\lor$ B).

5. Los sistemas C con A ≤ C y B ≤ C son: (123) (4) y (1234).

6.Sí, es cierto que en cada caso (A$\lor$ B) ≤ C.

Ejercicio 1.7

1. verdadero$\lor$ falso = verdadero.
2. falso$\lor$ verdadero = verdadero.
3. verdadero$\lor$ verdadero = verdadero.
4. falso$\lor$ falso = falso.

Ejercicio 1.10

1. Esto es cierto: un número natural es exactamente un entero que es al menos 0.

2. Esto es falso: 0$\in$$\mathbb{N}$ pero 0$\not \in$ {n$\in$$\mathbb{Z}$ | n ≥ 1}.

3. Esto es cierto: no hay elementos de$\mathbb{Z}$ estrictamente entre 1 y 2.

Ejercicio 1.11

1. Los ocho subconjuntos de B := {1, 2, 3} son

Ø, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}.

2. La unión de {1, 2, 3} y {1} es {1, 2, 3}$\bigcup$ {1} = {1,2,3}.

3. Los seis elementos de {h, 1} × {1, 2, 3} son

(h, 1), (h, 2), (h, 3), (1, 1), (1, 2), (1, 3).

4. Los cinco elementos de {h, 1} {1, 2, 3} son

(h, 1), (1, 1), (1, 2), (2, 2), (3, 2).

5. Los cuatro elementos de {h, 1}$\bigcup$ {1, 2, 3} son

h, 1, 2, 3.

Ejercicio 1.16

Supongamos que A es un conjunto y {A$_{p}$}$_{p \in P}$ y {A ′$_{p'}$}$_{p' \in P'}$ son dos particiones de A tal manera que por cada $\in$p P existe un p ′$\in$ P ′ con A$_{p}$ = A ′$_{p'}$.

1. Dado p$\in$ P, supongamos que teníamos p ′$_{1}$, p ′$_{2}$$\in$ P ′tal que A$_{p}$ = A ′$_{p'_{1}}$ y A$_{p}$ = A′$_{p'_{2}}$. Bueno entonces A$_{p'_{1}}$ = A$_{p'_{2}}$, entonces en particular A$_{p'_{1}}$ A$_{p'_{2}}$ = A =$_{p'_{1}}$ A. Por la definición de partición (1.14), A$_{p'_{1}}$$\neq$ Ø, y sin embargo si $_{1}$$\neq$p p$_{2}$ entonces $_{p'_{1}}$A A$_{p'_{2}}$ = Ø. Esto no puede ser, así que debemos tener p ′$_{1}$ = p ′$_{2}$, como se desee.

2. Supongamos dado $\in$p ′ P ′; queremos mostrar que hay un p$\in$ P tal que A$_{p}$ = A′$_{p'}$.

Dado que A ′$_{p'}$$\neq$ Ø no está vacío por definición, podemos escoger algunos a $\in$A ′$_{p'}$; desde $_{p'}$$\subseteq$A ′ A, tenemos $\in$una A.

Por último, desde A =$\bigcup_{p \in P} A_{p}$, hay alguna p con $\in$una$_{p}$ A.

Este es nuestro candidato p; ahora demostramos que A$_{p}$ = A ′$_{p'}$.

Por supuesto hay algo de p ′′$\in$ P ′ con A$_{p}$ = A ′$_{p'}$, por lo que ahora $\in$un A′$_{p''}$ y $\in$un A′$_{p' '}$, entonces a $\in$$_{p'}$A ′ A ′$_{p''}$. Nuevamente por definición, tener una intersección no vacía significa p ′ = p ′′. Por lo que concluimos que A$_{p}$ = A ′$_{p'}$.

Ejercicio 1.17

Los pares (a, b) tales que a ∼ b son:

(11, 11) (21, 21) (12, 11) (12, 12) (13, 13)

(21, 21) (22, 22) (12, 23) (23, 22) (23, 23)

Ejercicio 1.20

1. Un aspecto en la definición de las partes es que están conectadas, y un aspecto de eso es que no están vacías. Entonces cada parte A no$_{p}$ está vacía.

2. Supongamos que p$\neq$ q, es decir, A p y A q no son exactamente el mismo conjunto. Para probar A$_{p}$ A$_{q}$ = Ø, suponemos lo contrario y derivamos una contradicción.

Entonces supongamos que existe $\in$una$_{p}$ A A$_{q}$; mostraremos que A$_{p}$ = A$_{q}$, lo que contradice una hipótesis anterior. Para demostrar que estos dos subconjuntos son iguales, basta con mostrar que un ′$\in$ A$_{p}$ iff a ′ $\in$A$_{q}$ para todos a ′$\in$ A.

Supongamos $\in$un ′ A$_{p}$; entonces porque A$_{p}$ está conectado, tenemos un ∼ a ′. Y debido a$_{q}$ que A está cerrada,$\in$ a ′$_{q}$ A.

En el camino, si un ′$\in$ A$_{q}$ entonces porque A$_{q}$ está conectado y A$_{p}$ está cerrado, un ′$\in$ A$_{p}$, y ya terminamos.

3. Para mostrar que A =$\bigcup_{p \in P} A_{p}$, basta con mostrar que para cada una$\in$ A, hay algo de p ∈ P tal que a ∈ A$_{p}$.

Dijimos que P era el conjunto de subconjuntos cerrados y conectados de A, por lo que basta con mostrar que hay algún subconjunto cerrado y conectado que contiene a.

Dejar X: = {a ′$\in$ A | a ′ ∼ a}; afirmamos que está cerrado y conectado y contiene a. Para ver X está cerrado, supongamos a ′$\in$ X y b ∼ a ′; luego b ∼ a por transitividad y simetría de ∼, así que b$\in$ X. Para ver que X está conectado, supongamos b, c$\in$ X; luego b ∼ a y c ∼ a así que b ∼ c por la transitividad y simetría de ∼. Finalmente, una$\in$ X por la reflexividad de ∼.

Ejercicio 1.24

1. La función única Ø → {1} es inyectora pero no suryectiva.

2. La función única {a, b} → {1} es suryectiva pero no inyectiva.

3. Estas segunda y tercera no son funciones; la primera y la cuarta son funciones.

$Screen Shot 2021-02-02 a las 2.09.58 PM.png$

4. Ni el segundo ni el tercero es 'total'. Además, el segundo no es determinista. La primera es una función que no es inyectiva y no suryectiva. La cuarta es una función que es a la vez inyectiva y suryectiva.

Ejercicio 1.25

Por Definición 1.22, una función f: A → Ø es un subconjunto F$\subseteq$ A × Ø tal que para todos a $\in$A, existe un único b$\in$ Ø con (a, b)$\in$ F .

Pero no hay elementos b$\in$$^{?}$ Ø, así que si F va a tener la propiedad anterior, tampoco puede haber a $\in$A; es decir, A debe estar vacía.

Ejercicio 1.27

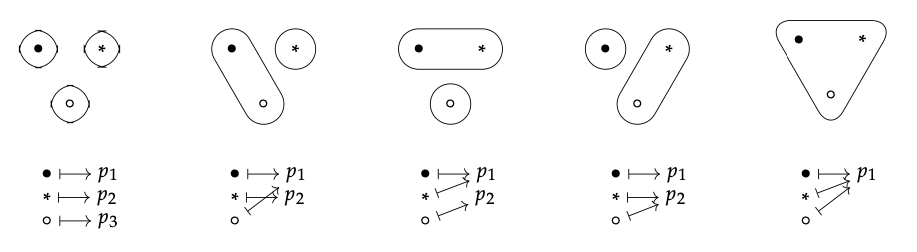
Debajo de cada partición, dibujamos una subyección correspondiente de {•, ∗, ◦}:

$Screen Shot 2021-02-02 en 2.17.04 PM.png$

Ejercicio 1.38

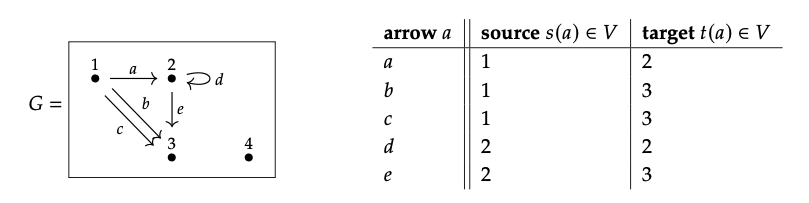
$Screen Shot 2021-02-03 a las 12.29.13 PM.png$

Ejercicio 1.40

El gráfico G del Ejercicio 1.38 es un extraño diagrama de Hasse porque tiene dos flechas 1 → 3 y un bucle, ambas de las cuales son “inútiles” desde un punto de vista de preorden. Pero eso no impide que nuestra fórmula funcione. El preorden (P, ≤) se da tomando P: = V = {1, 2, 3, 4} y escribiendo p ≤ q siempre que exista una ruta de p a q. Entonces:

1 ≤ 1, 1 ≤ 2, 1 ≤ 3, 2 ≤ 2, 2 ≤ 3, 3 ≤ 3, 4 ≤ 4

Ejercicio 1.41

Una colección de puntos, por ejemplo • • • es un diagrama de Hasse, es decir, para el orden discreto, es decir, para el orden donde x ≤ y iff x = y.

Ejercicio 1.42

Escribamos los cinco elementos de X como

$Screen Shot 2021-02-03 a las 12.34.22 PM.png$

Nuestro trabajo es anotar todos los 12 pares de x$_{1}$, x$_{2}$$\in$ X con x$_{1}$ ≤ x$_{2}$. Aquí están:

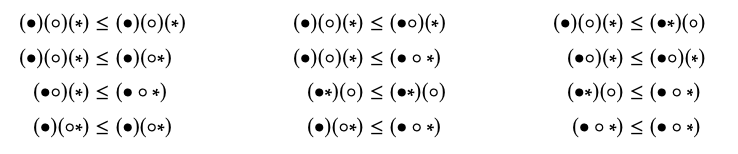
$Screen Shot 2021-02-03 a las 12.34.44 PM.png$

Ejercicio 1.44

El enunciado en el texto es casi correcto. Es correcto decir que un preorden discreto es aquel en el que x e y son comparables si y solo si x = y.

Ejercicio 1.46

$Screen Shot 2021-02-03 a las 12.37.53 PM.png$

No, no es un pedido total; por ejemplo 4$\nleq$ 6 y 6$\nleq$ 4.

Ejercicio 1.48

Sí, el pedido ≤ habitual es un pedido total en$\mathbb{R}$: por cada a, b$\in$$\mathbb{R}$ ya sea a ≤ b o b ≤ a.

Ejercicio 1.51

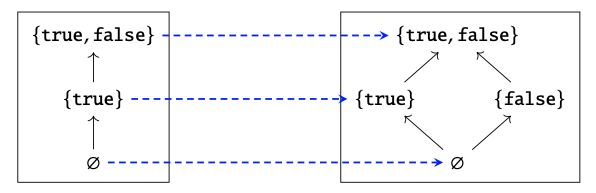
Los diagramas de Hasse para P (Ø), P {1} y P {1, 2} son

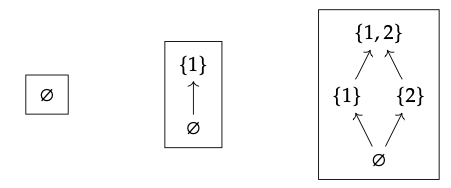
$Screen Shot 2021-02-03 a las 12.44.26 PM.png$

Ejercicio 1.53

¡La partición más basta en S corresponde a la función única! : S → {1}. La partición más fina en S corresponde a la función de identidad id$_{S}$: S → S.

Ejercicio 1.55

Si X tiene el preorden discreto, entonces cada subconjunto U de X es un conjunto superior: de hecho, si p$\in$ U, el único q tal que p ≤ q es p en sí mismo, así q está definitivamente en ¡U! Esto significa que U (X) contiene todos los subconjuntos de X, por lo que es exactamente el conjunto de potencia, U (X) = P (X).

Ejercicio 1.57

El pedido por adelantado del producto y su preorden del juego superior son:

$Screen Shot 2021-02-03 a las 12.49.16 PM.png$

Ejercicio 1.63

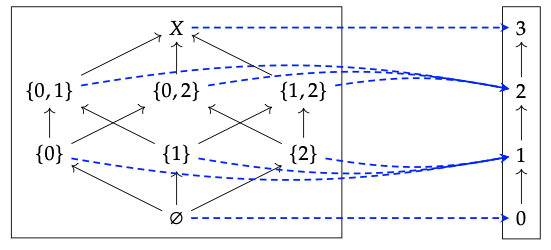
Con X = {0, 1, 2}, el diagrama de Hasse para P (X), el preorden 0 ≤ · · · ≤ 3, y el mapa de cardinalidad entre ellos se muestran a continuación:

$Screen Shot 2021-02-03 a las 12.50.06 PM.png$

Ejercicio 1.65

$Screen Shot 2021-02-03 a las 12.50.54 PM.png$

Ejercicio 1.66

Dejar q$\in$ ↑ p, y supongamos q ≤ q ′. Desde q$\in$ ↑ p, tenemos p ≤ q. Así por transitividad p ≤ q ′, así q ′$\in$ ↑ p. Así ↑ p es un conjunto superior.
Supongamos p ≤ q en P; esto significa que q ≤$^{op}$ p en$^{op}$ P. Debemos demostrar que ↑ q$\subseteq$ ↑ p. Tome cualquier q ′ $\in$↑ q. Entonces q ≤ q ′, así por transivitiy p ≤ q ′, y por lo tanto q ′$\in$ ↑ p. Así ↑ q$\subseteq$ ↑ p.
Monotonicidad de ↑ dice que p ≤ p ′ implica ↑ (p ′)$\subseteq$ ↑ (p). Debemos probar la otra dirección, que si p$\nleq$ p ′ entonces ↑ (p ′)$\subseteq$ ↑ (p). Esto es sencillo, ya que por reflexividad siempre tenemos p ′$\in$ ↑ (p ′), pero si p$\nleq$ p ′, entonces p ′$\not \in$ ↑ (p), entonces ↑ (p ′)$\not \subseteq$ ↑ (p).
El mapa ↑: P$^{op}$ → U (P) se puede representar:

$Screen Shot 2021-02-03 al 1.06.55 PM.png$

Ejercicio 1.67

Supongamos que (P, ≤$_{P}$) es un preorden discreto y que (Q, ≤$_{Q}$) es cualquier preorden.

Queremos mostrar que cada función f: P → Q es monótona, es decir, que si p$_{1}$ ≤$_{P}$ p$_{2}$ entonces f (p$_{1}$) ≤ Q f (p$_{2}$).

Pero en P tenemos p$_{1}$ ≤$_{P}$ p$_{2}$ iff p$_{1}$ = p$_{2}$; eso es lo que significa discreto.

Si p$_{1}$ ≤$_{P}$ p$_{2}$ entonces p$_{1}$ = p$_{2}$, entonces f (p$_{1}$) = f (p$_{2}$), entonces f (p$_{1}$) ≤ f ( p$_{2}$).

Ejercicio 1.69

Sea X =$\mathbb{Z}$ = {..., −2, −1, 0, 1,...} sea el conjunto de todos los enteros, y que Y = {n, z, p}; let f: X → Y envíe números negativos a n, cero a z y enteros positivos a p. Esto es surytivo porque los tres elementos de Y son golpeados.

Consideramos dos particiones de Y, a saber P: = (nz) (p) y Q: = (np) (z). Técnicamente, se trata de notación para$\{\{n, z\},\{p\}\}$ y$\{\{n, p\},\{z\}\}$ como conjuntos de subconjuntos disjuntos cuya unión es Y. Sus particiones retraídas son$f^{*}$ P =(..., -2, -1, 0) (1, 2,...) y$ f^{*}Q$ = (0) (..., -2, -1,1,2,...), o técnicamente
$f^{*}(P)$ =$\{\{x \in \mathbb{Z} \mid x \leq 0\}$,$\{x \in \mathbb{Z} \mid x \geq 1\}\}$ y $f^{*}(Q)$=$\{\{0\},\{x \in \mathbb{Z} \mid x \neq 0\}\}$.

Ejercicio 1.71

Tenemos preordenes (P, ≤$_{P}$), (Q, ≤$_{Q}$) y (R, ≤$_{R}$), y tenemos mapas monótonos f: P → Q y g: Q → R.

1. Para ver que id$_{P}$ es monótona, necesitamos mostrar que si p$_{1}$ ≤$_{P}$ p$_{2}$ entonces id$_{P}$ (p$_{1}$) ≤ id$_{P}$ (p$_{2}$). Pero id$_{P}$ (p) = p para todos p$\in$ P, así que esto es claro.

2. Tenemos que p$_{1}$ ≤$_{P}$ p$_{2}$ implica f (p$_{1}$) ≤$_{Q}$ f (p$_{2}$) y que q$_{1}$ ≤$_{Q}$ q$_{2}$ implica g (q $_{1}$) ≤$_{R}$ g (q$_{2}$).

Por sustitución, p$_{1}$ ≤$_{P}$ p$_{2}$ implica g (f (p 1)) ≤$_{R}$ g (f (p 2)) que es exactamente lo que se requiere para que (f; g) sea monótona.

Ejercicio 1.73

Necesitamos demostrar que si (P, ≤$_{P}$) es tanto esquelético como daga, entonces es discreto. Entonces supongamos que es esquelético, es decir p$_{1}$ ≤ p$_{2}$ y p$_{2}$ ≤ p$_{1}$ implica p$_{1}$ =$_{2}$ p. Y supongamos que es daga, es decir p$_{1}$ ≤ p$_{2}$ implica p$_{2}$ ≤$_{1}$ p. Bueno entonces p$_{1}$ ≤ p$_{2}$ implica p$_{1}$ = p$_{2}$, y esta es exactamente la definición de P siendo discreto.

Ejercicio 1.77

El mapa Φ de la Sección 1.1.1 tomó particiones de {•, ∗, ◦} y devolvió verdadero o falso en función de si • estaba o no en la misma partición que ∗. Necesitamos ver que en realidad es un mapa monótona Φ: Prt ({•, ∗, ◦}) →$\mathbb{B}$. Entonces supongamos que P, Q son particiones con P ≤ Q; necesitamos mostrar que si Φ (P) = true entonces Φ (Q) = true. Por definición P ≤ Q significa que P es más fino que Q: es decir, P diferencia más cosas, y Q agrupa más cosas juntas. Técnicamente, x ∼ P y implica x ∼ Q y para todos x, y$\in$ {•, ∗, ◦}. Aplicando esto a •, ∗ da el resultado.

Ejercicio 1.79

Dada una función f: P → Q, tenemos f$^{∗}$: U (Q) → U (P) dada por U$\longmapsto$ f$^{−1}$ (U). Pero los conjuntos superiores en Q se clasifican por mapas monótonos u: Q →$\mathbb{B}$, y de manera similar para P; nuestro trabajo es demostrar que f$^{∗}$ (U) se da componiendo el clasificador u con f. Dado un conjunto superior U$\subseteq$ Q, deja que u: Q →$\mathbb{B}$ sea el mapa monótona correspondiente, que envía q$\longmapsto$ true iff q$\in$ U.

Entonces (f; u): P →$\mathbb{B}$ envía p$\longmapsto$ true iff f (p)$\in$ U; corresponde al conjunto superior {p$\in$ P | f (p)$\in$ U} que es exactamente f$^{−1}$ (U).

Ejercicio 1.80

1. 0 es un límite inferior para$S=\left\{\frac{1}{n+1} \mid n \in \mathbb{N}\right\}$ porque 0 ≤$\frac{1}{n+1}$ para cualquier n$\in$$\mathbb{N}$.

2. Supongamos que b es un límite inferior para S; queremos ver que b ≤ 0. Si uno cree al contrario que 0 < b, entonces considere 1/ b; es un número real para que podamos encontrar un número natural n que sea mayor 1/ b < n < n + 1. Esto implica 1 < b (n + 1) y por lo tanto$\frac{1}{n+1}$ < b, pero eso es una contradicción de que b es un límite inferior para S. ¡El falso creyente es derrotado!

Ejercicio 1.85

Tenemos un preorden (P, ≤), un elemento p$\in$ P, y un subconjunto A = {p} con un elemento.

Para ver que$\bigwedge$ A$\cong$ p, necesitamos mostrar que p ≤ a para todos a $\in$A y que si q ≤ a para todos a $\in$A entonces q ≤ p . Pero la única a$\in$ A es a = p, así que ambas son obvias.
Sabemos que p es un encuentro de A, así que si q es también un encuentro de A entonces q ≤ a para todos a $\in$A así q ≤ p; similarmente p ≤ a para todos a$\in$ A, entonces p ≤ q. Entonces por definición tenemos p$\cong$ q, y ya que (P, ≤) es un orden parcial, p = q.
Los hechos análogos son ciertos cuando$\bigwedge$ se sustituye por$\bigvee$; el único cambio en el argumento es reemplazar ≤ por ≥ y 'reunirse' por 'unirse' en todas partes.

Ejercicio 1.90

El encuentro de 4 y 6 es el número más alto en el orden que divide a ambos; los números que dividen a ambos son 1 y 2, y 2 es mayor, por lo que 4$\land$ 6 = 2. Razonamiento similar muestra que 4$\lor$ 6 = 12.

El encuentro es el 'mayor divisor común' y la unión es el 'múltiplo menos común', y esto aguanta para todos los pares m, n$\in$$\mathbb{N}$ no solo 4, 6.

Ejercicio 1.94

Dado que f es monótona, los hechos que a ≤ a$\lor$ b y b ≤ a$\lor$ b implican que f (a) ≤ f (a$\lor$ b) y f b) ≤ f (a$\lor$ b). Pero por definición de unión, f (a)$\lor$ f (b) es el elemento más grande con esa propiedad, por lo que f (a)$\lor$ f (b) ≤ f (a$\lor$ b), como deseado.

Ejercicio 1.98

Por analogía con el Ejemplo 1.97, el derecho adjunto para (3 × −) debe ser −/3. Pero para probar que esto es correcto, debemos demostrar que para cualquier r$\in$$\mathbb{R}$ y z$\in$$\mathbb{Z}$ tenemos z ≤ r /3 iff 3 ∗ z ≤ r. Supongamos que el entero más grande por debajo de r /3 es z ′: = r /3. Entonces z ≤ z ′ implica 3∗ z ≤ 3∗ z ′ ≤ 3∗ r /3 = r, dando una dirección. Para el otro, supongamos 3 ∗ z ≤ r. Luego dividiendo ambos lados por 3, tenemos z = 3 ∗ z /3 ≤ r /3. Dado que z es un entero por debajo de r /3 está por debajo de r /3 porque r /3 es el mayor entero por debajo de r /3, y ya terminamos.

Ejercicio 1.99

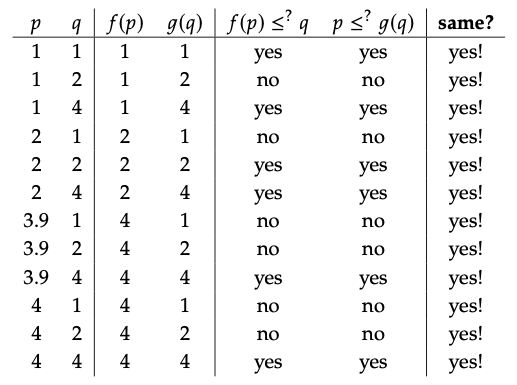
1. Necesitamos verificar que para los nueve pares {(p, q) | 1 ≤ p ≤ 3 y 1 ≤ q ≤ 3} tenemos f (p) ≤ q iff p ≤ g (q), donde f y g son las funciones se muestra aquí:

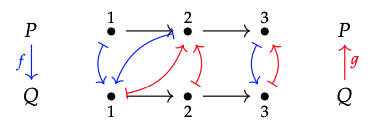
$Screen Shot 2021-02-03 en 2.33.39 PM.png$

Cuando p = q = 1 tenemos f (p) = 1 y g (q) = 2, así que tanto f (p) = 1 ≤ 1 = q y p = 1 ≤ g (q); ¡funciona! El mismo tipo de historia ocurre cuando (p, q) es (1, 2), (1, 3), (2, 1), (2, 2), (2, 3) y (3, 3). Una historia diferente sucede para p = 3, q = 1 y p = 3, q = 2. En esos casos f (p) = 3 y g (q) = 2, y ninguna desigualdad se mantiene: f (p)$\nleq$ q y p$\nleq$ g (q). Pero eso está bien, todavía tenemos f (p) ≤ q iff p ≤ g (q) en los nueve casos, según se desee.

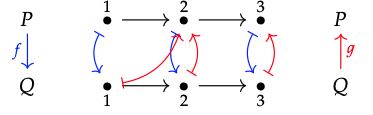
$Screen Shot 2021-02-03 en 2.34.37 PM.png$

Aquí f no se deja unido a g porque f (2)$\nleq$ 1 sino 2 ≤ g (1).

Ejercicio 1.101

Supongamos que tenemos un mapa monótono L:$\mathbb{Z}$ →$\mathbb{R}$ que se deja colindante a −/3y veamos qué pasa. Escribiendo C (r) :=r /3, entonces para todos z$\in$$\mathbb{Z}$ y r$\in$$\mathbb{R}$ tenemos L (z) ≤ r iff z ≤ C (r) por definición de amonestación. Así que toma z = 1 y r = .01; luego r /3 = 1 entonces z ≤ C (r), y por lo tanto L (z) ≤ r, es decir L (1) ≤ 0.01. De la misma manera L (1) ≤ r para todos r > 0, entonces L (1) ≤ 0. Por definición de amontonamiento 1 ≤ C (0) = 0/3= 0, una contradicción.
No hay izquierda colindante, porque a partir de una arbitraria, derivamos una contradicción.

Ejercicio 1.103

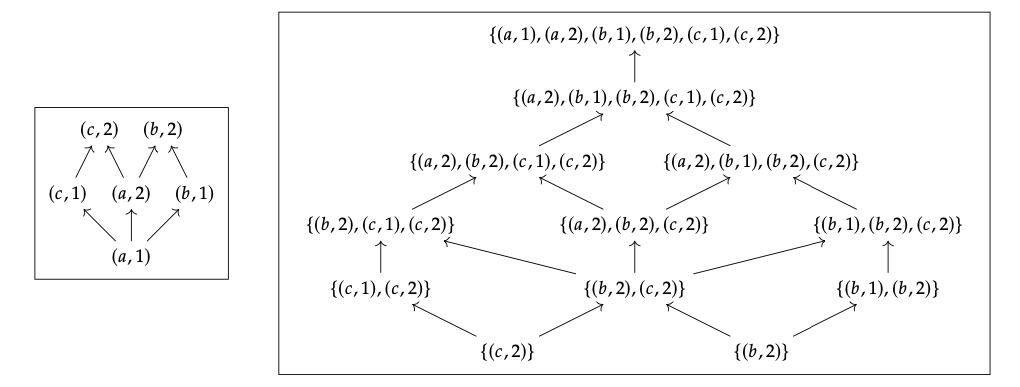
Tenemos S = {1, 2, 3, 4}, T = {12, 3, 4}, y g: S → T la función “obvia” entre ellas; ver Ejemplo 1.102. Tome c$_{1}$, c$_{2}$, c$_{3}$, c$_{4}$ como las siguientes particiones:

$Screen Shot 2021-02-03 en 2.51.43 PM.png$

Entonces las particiones inducidas g! (c$_{1}$), g! (c$_{2}$), g! (c$_{3}$), y g! c$_{4}$) en T son:

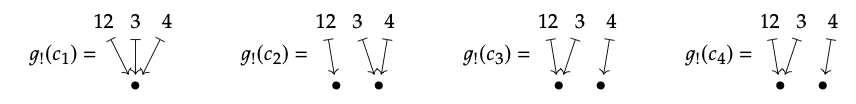
$Screen Shot 2021-02-03 en 2.52.11 PM.png$

Ejercicio 1.106

1. Elegimos la siguiente partición c en S y calculamos su push forward g! c):

$Screen Shot 2021-02-03 at 7.05.09 PM.png$

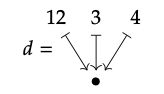
2. Que d sea la partición como se muestra, que se eligió para ser más tosca que g! c).

$Screen Shot 2021-02-03 a las 7.06.20 PM.png$

3. Que e sea la partición como se muestra, que se eligió para no ser más tosca que g! c).

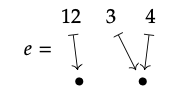
$Screen Shot 2021-02-03 at 7.06.25 PM.png$

4. Aquí están$g^{∗}(d)$ y$g^{∗}(e)$:

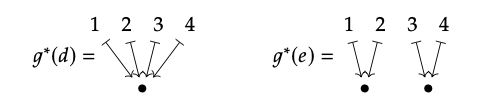
$Screen Shot 2021-02-03 at 7.06.29 PM.png$

5. Comparando c, la partición izquierda en la parte 1., con$g^{∗}(d)$ y$g^{∗}(e)$, efectivamente tenemos c ≤$g^{∗}(d)$ pero c$\nleq$$g^{∗}(e)$), según se desee.

Ejercicio 1.109

Supongamos que P y Q son preórdenes, y que$f: P \leftrightarrows Q: g$ son mapas monótonos.

Supongamos que f se deja junto a g. Por definición esto significa f (p) ≤ q iff p ≤ g (q), para todos p$\in$ P y q$\in$ Q. Entonces comenzando con el hecho de reflexividad g (q) ≤ g (q), la definición con p: = g (q) da f (g (q)) ≤ q para todos q.
Supongamos que p ≤ g (f (p)) y f (g (q)) ≤ q para todos p$\in$ P y q$\in$ Q. Primero queremos mostrar que p ≤ g (q) implica f (p) ≤ q, así que supongamos p ≤ g (q). Luego aplicando el mapa monótona f a ambos lados, tenemos f (p) ≤ f (g (q)), y luego por transitividad f (g (q)) ≤ q implica f (p) ≤ q, según se desee. La otra dirección es similar.

Ejercicio 1.110

Supongamos que f: P → Q tiene dos anexos derechos, g, g ′: Q → P. Queremos mostrar que g (q)$\cong$ g ′ (q) para todos q$\in$ Q. Demostraremos g (q) ≤ g ′ (q); la desigualdad g ′ (q) ≤ g (q) es similar. Para ello, utilizamos el hecho de que p ≤ g ′ (f (p)) y f (g (q)) ≤ q para todos p, q por Eq. (1.108). Entonces el truco es razonar de la siguiente manera:
g (q) ≤ g ′ (f (g (q))) ≤ g ′ (q).
Es lo mismo para los colindantes izquierdos.

Ejercicio 1.112

Supongamos que f: P → Q se deja unido a g: Q → P. Sea A$\subseteq$ P cualquier subconjunto y que j: =$\bigvee$ A sea su unión.

Entonces como f es monótona f (a) ≤ f (j) para todos a $\in$A, entonces f (j) es un límite superior para el conjunto f (A). Queremos mostrar que es el límite inferior superior, así que toma cualquier otro límite superior b para f (A), es decir, tenemos f (a) ≤ b para todos $\in$a A. Entonces por definición de amontonamiento, también tenemos a ≤ g (b) para todos $\in$a A. Por definición de unión, tenemos j ≤ g (b). Nuevamente por definición de amontonamiento f (j) ≤ b, según se desee.

Ejercicio 1.114

Queremos mostrar que en la siguiente imagen, g es realmente justo colindante a f:

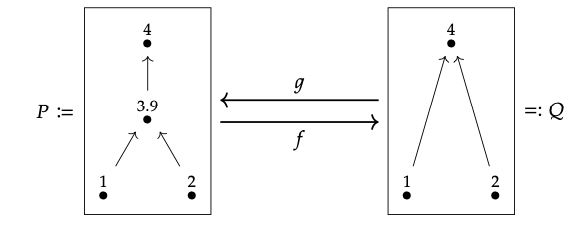
$Screen Shot 2021-02-03 a las 8.13.37 PM.png$

Aquí g conserva etiquetas y f redondea 3.9 a 4.
Hay doce cosas diminutas para verificar: por cada $\in$p P y $\in$q Q, necesitamos ver que f (p) ≤ q iff p ≤ g (q).

$Screen Shot 2021-02-03 a las 8.14.37 PM.png$

Ejercicio 1.118

Considere la función que se muestra a continuación, que “proyecta directamente hacia abajo”:

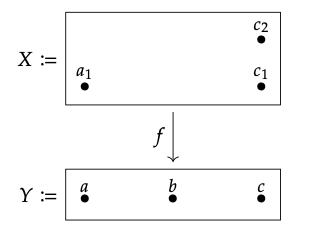
$Screen Shot 2021-02-03 a las 8.15.17 PM.png$

1. Sea B$_{1}$ := {a, b} y B$_{2}$ := {c} .Entonces f$^{∗}$ (B$_{1}$) = {a$_{1}$} y f$^{∗}$ (B$_{2}$) = {c$_{1}$, c$_{2}$}.

2. Dejar A$_{1}$ := Ø y A$_{1}$ := {a$_{1}$, c$_{1}$}. Entonces f$_{!}$ (A$_{1}$) := Ø y f$_{!}$ (A$_{2}$) = {a, c}.

3. Con los mismos A$_{1}$ y A$_{2}$, calculamos f$^{∗}$ (A$_{1}$) = {b} y f$^{∗}$ (A$_{2}$) = {a, b}.

Ejercicio 1.119

Supongamos que f: P → Q se deja unido a g: Q → P.

Es parte de la definición de amonestación (Proposición1.107) que p ≤ g (f (p)), y por supuesto g (f (p)) y (f; g) (p) significan lo mismo.
Queremos mostrar que g (f (g (f (p)))) ≤ g (f (p)) y g (f (p)) ≤ g (f (g (f (p))) para todos p. Este último es solo el hecho de que p ′ ≤ g (f (p ′)) para cualquier p ′, aplicado con g (f (p)) en lugar de p′. El primero usa que f (g (q)) ≤ q, con f (p) sustituido por q: esto da f (g (f (p))) ≤ f (p), y luego aplicamos g a ambos lados.

Ejercicio 1.124

Denotamos tuplas (a, b) por ab por razones espaciales. Entonces la relación {(1, 1), (1, 2), (2, 1)} se denotará {11, 12, 21}.

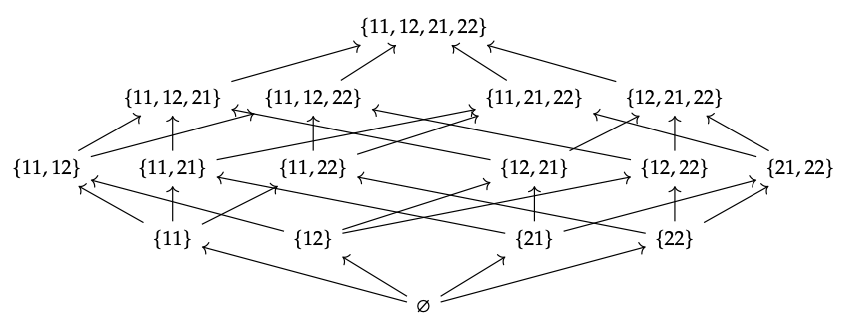
$Screen Shot 2021-02-03 a las 8.37.32 PM.png$

Ejercicio 1.125

Vamos S: = {1, 2, 3}.

1. Dejar ≤ ser el preorden con 1 ≤ 2, y por supuesto 1 ≤ 1, 2 ≤ 2, y 3 ≤ 3. Entonces U (≤) = {(1, 1), (1, 2), (2, 2), (3, 3)}.

Sea Q: = {(1,1)} y Q ′: = {(2,1)}.
El cierre Cl (Q) de Q es el preorden más pequeño que contiene (1,1), que es Cl (Q) = {(1,1), (2,2), (3,3)}.
De igual manera, Cl (Q ′) = {(1, 1), (2, 1), (2, 2), (3, 3)}. Es fácil ver que Cl (Q)$\sqsubseteq$\) ≤ porque cada par ordenado en Cl (Q) también está en ≤.
Es fácil ver que Cl (Q ′)$\not \sqsubseteq$ ≤ porque el par ordenado (2,1) está en Cl (Q ′) pero no está en ≤.