8.7: Soluciones para el Capítulo 7
- Page ID
- 112258
En el diagrama conmutativo a continuación, supongamos que el cuadrado (B, C, B′, C′) es un retroceso:
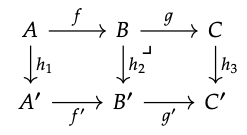
Necesitamos demostrar que el cuadrado (A, B, A′, B′) es un retroceso si el rectángulo (A, C, A′, C′) es un retroceso.
Supongamos primero que (A, B, A′, B ′) es un retroceso, y tomar cualquier (X, p, q) como en el siguiente diagrama:
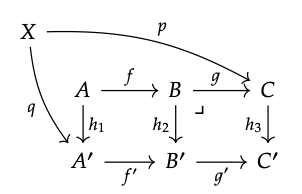
donde q; f; g '= p; h\(_{3}\). Luego, por la propiedad universal del retroceso (B, C, B ', C'), obtenemos una flecha punteada única r haciendo que el diagrama de la izquierda a continuación conmute:
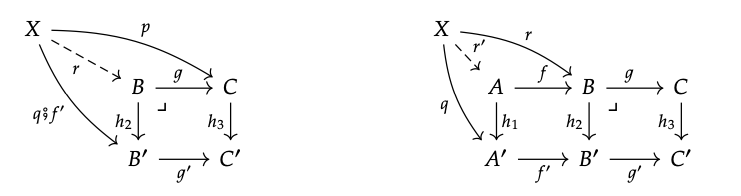
En otras palabras r; h\(_{2}\) = g; f ′ y r; g = p. Luego, por la propiedad universal del retroceso (A, B, A ′, B ′), obtenemos una flecha punteada única r ': X → A haciendo que el diagrama de la derecha conmute, es decir, r'; f = r y r '; h\(_{1}\) = q. Esto da la existencia de una r con la propiedad requerida, r '; f = r y r'; f = r; g = p. Para ver la singularidad, supongamos dado otros morfismos r\(_{0}\) tales que r\(_{0}\); f; g = p y r\(_{0}\); h\(_{1}\) = q:
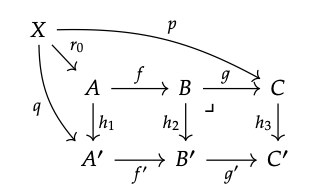
Entonces por la singularidad de r, debemos tener r\(_{0}\); f = r, y luego por la singularidad de r ′, debemos tener r\(_{0}\) = r ′. Esto prueba el primer resultado.
El segundo es similar. Supongamos que (A, C, A′, C′) y (B, C, B′, C ′) son retrocesos y supongamos que se le da un diagrama conmutativo de la siguiente forma:
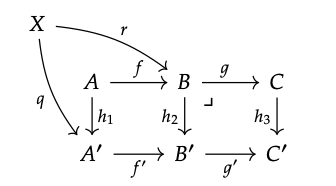
es decir, donde r; h\(_{2}\) = q; f ′. Entonces dejando p: = r; g, tenemos
p; h\(_{3}\) = r; g; h\(_{3}\) = r; h\(_{2}\); g '= q; f'; g '
así que por la propiedad universal del retroceso (A, C, A ′, C ′), hay un morfismo único r ′: X → A tal que r '; f; g = p y r\(_{0}\); h\(_{1}\) = q, como se muestra:
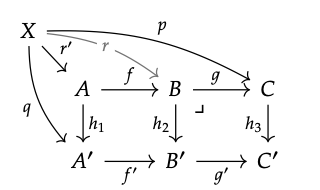
Pero ahora vamos a r\(_{0}\) := r '; f. Satisface r\(_{0}\); g = p y r\(_{0}\); h\(_{2}\) = q; f ', y r satisface las mismas ecuaciones: r; g = p y r; h\(_{2}\) = q; f ′. De ahí por la propiedad universal del retroceso (B, C, B ′, C ′) r\(_{0}\) = r ′. De ello se deduce que r 'es un retroceso del cuadrado (A, B, A′, B′), según se desee.
Una función f: A → B es iff inyectable para todos a\(_{1}\), a \(_{2}\)\(\in\)A, si f (a\(_{1}\)) = f (a\(_{2}\)) entonces a\(_{1}\) = a\(_{2}\).
Es un monomorfismo iff para todos los conjuntos X y funciones g\(_{1}\), g\(_{2}\): X → A, si g\(_{1}\); f = g\(_{2}\); f entonces g\(_{1}\) = g\(_{2}\). En efecto, esto proviene directamente de la propiedad universal del retroceso de la Definición 7.5"

porque la flecha discontinua es forzada a igualar tanto g\(_{1}\) como g\(_{2}\), forzando así g\(_{1}\) = g\(_{2}\).
1. Supongamos que f es un monomorfismo, deja que a\(_{1}\), a \(_{2}\)\(\in\)A sean elementos, y supongamos f (a\(_{1}\)) = f (a\(_{2}\)).
Sea X = {∗} un conjunto de elementos, y deje que g\(_{1}\), g\(_{2}\): X → A sea dado por g\(_{1}\) (∗) := a\(_{1}\) y g\(_{2}\) (∗) := a\(_{2}\). Entonces g\(_{1}\); f = g\(_{2}\); f, entonces g\(_{1}\) = g\(_{2}\), entonces a\(_{1}\) = a\(_{2}\).
2. Supongamos que f es una inyección, deja que X sea un conjunto y, y que g\(_{1}\), g\(_{2}\): X → A sea tal que g\(_{1}\); f = g\(_{2}\); f . Tendremos g\(_{1}\) = g\(_{2}\) si podemos mostrar que g\(_{1}\) (x) = g\(_{2}\) (x) por cada x\(\in\) X. Así que toma cualquier \(\in\)x X; ya que f\(_{1}\) (g (x)) = f\(_{2}\) (g (x)) y f es inyectable, tenemos g\(_{1}\) (x) = g \(_{2}\)(x) según se desee.
1. Supongamos que tenemos un retroceso como se muestra, donde i es un isomorfismo:
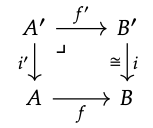
\(^{-1}\)Sea j: = i la inversa de i, y considere g := (f; j): A → B ′. Entonces g; i = f, así por la existencia parte de la propiedad universal, hay un mapa j: A → A 'tal que j'; i '= id\(_{A}\) y j'; f '= f; j. Estaremos hechos si podemos mostrar i '; j' = id\(_{A'}\). Se comprueba que (i '; j'); i '= i' y eso (i '; j'); f '= i'; f ; j = f '; i; j = f'.
Pero id\(_{A'}\) también satisface esas propiedades: id\(_{A'}\); i '= i' e id\(_{A'}\); f '= f', así por la parte de singularidad de la propiedad universal, (i '; j') = id\(_{A'}\).
2. Tenemos que mostrar que el siguiente diagrama es un retroceso:
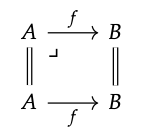
Así que toma cualquier objeto X y los morfismos g: X → A y h: X → B tal que g; f = h; id\(_{B}\).
Necesitamos mostrar que hay un morfismo único r: X → A tal que r; id\(_{A}\) = g y r; f = h. Eso es fácil: el primer requisito fuerza r = g y luego se cumple el segundo requisito.
Considere el diagrama que se muestra a la izquierda, en el que los tres cuadrados son retrocesos:
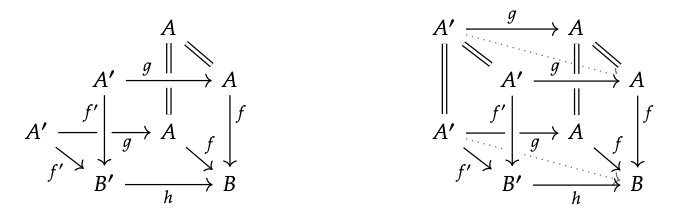
Los cuadrados frontal e inferior son los mismos, el supuesto retroceso, y el cuadrado de la derecha es un retroceso porque f se asume monic. Podemos completarlo al diagrama conmutativo que se muestra a la derecha, donde el cuadrado posterior y el cuadrado superior son retrocesos por el Ejercicio 7.7. Nuestro objetivo es mostrar que el cuadrado de la izquierda es un retroceso.
Para ello, utilizamos dos aplicaciones del lema de pegado, Ejercicio 7.4. Dado que la cara derecha es un retroceso y la cara posterior es un retroceso, el rectángulo diagonal (ligeramente dibujado) también es un retroceso. Dado que la cara frontal es un retroceso, la cara izquierda también es un retroceso.
A continuación se presenta una factorización epimono de f:
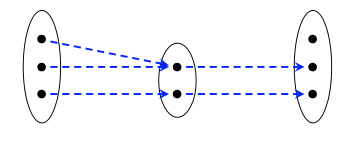
1. Si V es una quantale con las propiedades declaradas, entonces
• I sirve como elemento superior: v ≤ I para todos \(\in\)v V.
• v w sirve como una operación de reunión, es decir, satisface la misma propiedad universal que\(\land\), a saber, v w es un límite inferior mayor para v y w.
Ahora la operación satisface la misma propiedad universal que la exponenciación (hom-object), es decir, v ≤ (w -o x) iff v W ≤ x. Entonces V es una categoría cerrada cartesiana, y por supuesto es una preorden.
2. No todos los prepedidos cerrados cartesianos provienen de una quantale con las propiedades declaradas, porque los quantales tienen todas las uniones y las preordenes cerradas cartesianas no necesitan. Encontrar un contraejemplo de un preorden cerrado cartesiano al que le faltan algunos dientes, requiere algo de ingenio, pero se puede hacer. Aquí hay uno que se nos ocurrió:
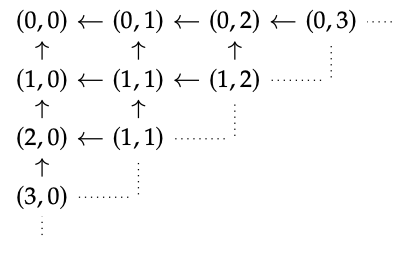
Este es el preorder del producto\(\mathbb{N}\)\(^{op}\) ×\(\mathbb{N}\)\(^{op}\): sus objetos son pares (a, b)\(\in\)\(\mathbb{N}\) ×\(\mathbb{N}\) con (a, b) ≤ (a ′, b ′) iff, en el pedido habitual\(\mathbb{N}\) tenemos a ′ ≤ a y b ′ ≤ b. Pero solo puedes mirar el diagrama.
Tiene un elemento superior, (0, 0), y tiene conjuntos binarios, (a, b)\(\land\) (a ′, b ′) = (max (a, a ′), max (b, b ′)). Pero no tiene elemento inferior, por lo que no tiene unión vacía. Así lo haremos si podemos mostrar que por cada x, y, existe el hom-object x -o y. La fórmula para ello es x -o y =\(\bigvee\) {w | w\(\land\) x ≤ y}, es decir, necesitamos que estas uniones particulares existan. Desde y\(\land\) x ≤ y, tenemos y ≤ x -o y. Así podemos sustituir la fórmula por x -o y =\(\bigvee\) {w | y ≤ w y w\(\land\) x ≤ y}. Pero el conjunto de elementos en\(\mathbb{N}\)\(^{op}\) ×\(\mathbb{N}\)\(^{op}\) que son mayores que y es finito y no vacío. \(^{2}\)Entonces esta es una unión finita no vacía, y\(\mathbb{N}\)\(^{op}\) ×\(\mathbb{N}\)\(^{op}\) tiene todas las uniones finitas no vacías: son dadas por inf.
\(\mathbb{B}\)Sea m:\(\mathbb{Z}\) → la función característica de la inclusión\(\mathbb{N}\)\(\subseteq\)\(\mathbb{Z}\).
1. \(\lceil{m(−5)}\rceil\)= falso. 2. \(\lceil{m(0)}\rceil\)= verdadero.
1. La función característica\(\lceil{id_{\mathbb{N}}\rceil\):\(\mathbb{N}\) →\(\mathbb{B}\) envía cada n\(\in\)\(\mathbb{N}\) a true.
2. ¡Vamos! \(_{\mathbb{N}}\): Ø →\(\mathbb{N}\) ser la inclusión del conjunto vacío. La función característica\(\lceil{!_{\mathbb{N}}\rceil\):\(\mathbb{N}\) →\(\mathbb{B}\) envía cada n\(\in\)\(\mathbb{N}\) a false.
1. El tipo de cosas (*? *) estamos buscando es un subobjeto de B, digamos A\(\subseteq\) B. Esto tendría una función característica, y estamos tratando de encontrar la A para la que la función característica es ¬:\(\mathbb{B}\) →\(\mathbb{B}\).
2. La pregunta ahora pregunta “¿qué es A?” La respuesta es {false}\(\subseteq\) B.
1. Aquí está la tabla de verdad para P = (P\(\land\) Q):

- ¡Sí!
- La función característica para P ⇒ Q es la función\(\lceil{⇒}\rceil\):\(\mathbb{B}\) ×\(\mathbb{B}\) →\(\mathbb{B}\) dada por la primera, segunda y cuarta columna de la Ec. (A.3).
- Clasifica el subconjunto {(true, true), (false, true), (false, false)\(\subseteq\)\(\mathbb{B}\) ×\(\mathbb{B}\).
Digamos que\(\lceil{E}\rceil\)\(\lceil{P}\rceil\),,\(\lceil{T}\rceil\):\(\mathbb{N}\) →\(\mathbb{B}\) clasificar respectivamente los subconjuntos E: = {n\(\in\)\(\mathbb{N}\) | n es par}, P: = {n\(\in\)\(\mathbb{N}\) | n es primo}, y T: = {n\(\in\)\(\mathbb{N}\) | n ≥ 10} de\(\mathbb{N}\).
1. \(\lceil{E}\rceil\)(17) = falso porque 17 no es par.
2. \(\lceil{P}\rceil\)(17) = verdadero porque 17 es primo.
3. \(\lceil{T}\rceil\)(17) = verdadero porque 17 ≥ 10.
4. El conjunto clasificado por (\(\lceil{E}\rceil\)\(\land\)\(\lceil{P}\rceil\))\(\lor\)\(\lceil{T}\rceil\) es el de todos los números naturales que están por encima de 10 o un primo par. Los tres elementos más pequeños de este conjunto son 2, 10, 11.
1. El análogo 1-dimensional de una\(\mathcal{E}\) -bola alrededor de un punto x\(\in\)\(\mathbb{R}\) es B (x,\(\mathcal{E}\)) := {x ′\(\in\) R || x − x ′ | <\(\mathcal{E}\)}, es decir, el conjunto de todos los puntos dentro\(\mathcal{E}\) de x .
2. Un subconjunto U\(\subseteq\)\(\mathbb{R}\) está abierto si, por cada x\(\in\) U hay algo\(\mathcal{E}\) > 0 tal que B (x,\(\mathcal{E}\))\(\subseteq\) U.
3. Sea U\(_{1}\) := {x\(\in\)\(\mathbb{R}\) | 0 < x < 2} y U\(_{2}\) := {x\(\in\)\(\mathbb{R}\) | 1 < x < 3}. Entonces U: = U\(_{1}\)\(\cup\) U\(_{2}\) = {x\(\in\)\(\mathbb{R}\) | 0 < x < 3}.
4. Que I = {1, 2, 3, 4,...} y para cada \(\in\)i dejo U: = {x\(\in\)\(\mathbb{R}\) |\(\frac{1}{i}\) < x < 1}, así tenemos U\(_{1}\) (\ subseteq\) U\(_{2}\) (\ subseteq\) U\(_{3}\) (\ subseteq\) · · ·.
Su unión es U: =\(\bigcup\)\(_{i \in I}\) U\(_{i}\) = {x\(\in\)\(\mathbb{R}\) | 0 < x < 1}.
1. La topología gruesa en X es aquella cuyos únicos conjuntos abiertos son X (\ subseteq\) X y Ø (\ subseteq\) X. Esta es una topología porque contiene los subconjuntos superior e inferior, se cierra bajo intersección finita (la intersección A B es Ø iff uno u otro es Ø), y se cierra bajo unión arbitraria (la unión\(\bigcup_{i \in I} A_{i}\) es X iff A \(_{i}\)= X para algunos i\(\in\) I).
2. La topología fina en X es aquella en la que cada subconjunto A (\ subseteq\) X se considera abierto. Todas las condiciones en una topología dicen “si tal y tal entonces tal y tal está abierto”, pero todas estas están satisfechas porque ¡todo está abierto!
3. Si (X, P (X)) es discreto, (Y, Op\(_{Y}\)) es cualquier espacio topológico, y f: X → Y es cualquier función entonces es continuo. En efecto, esto solo significa que para cualquier conjunto abierto U (\ subseteq\) Y la preimagen f\(^{ −1}\) (U) (\ subseteq\) X está abierta, y todo en X está abierto.
1. El diagrama de Hasse para la topología Sierpinsky es Ø → {1} → {1, 2}.
2. Un juego\(\left(U_{i}\right)_{i \in I}\) cubre U iff ya sea
• I = Ø y U = Ø; o
• U\(_{i}\) = U para algunos i\(\in\) I.
En otras palabras, la única forma en que alguna colección de estos conjuntos podría cubrir otro conjunto U es si esa colección contiene U o si U está vacía y la colección también está vacía.
Sea (X, Op) un espacio topológico, supongamos que Y (\ subseteq\) X es un subconjunto, y considerar la topología subespacial Op\(_{?∩Y}\).
1. Queremos demostrar que Y\(\in\) Op\(_{?∩Y}\). Necesitamos encontrar B\(\in\) Op tal que Y = B Y; esto es fácil, podrías tomar B = Y o B = X, o cualquier cosa intermedia.
2. Todavía necesitamos demostrar que Op\(_{?∩Y}\) contiene Ø y está cerrado bajo intersección finita y unión arbitraria. Ø = Ø Y, así de acuerdo a la fórmula, Ø\(\in\) Op\(_{?∩Y}\). Supongamos que A\(_{1}\), A\(_{2}\)\(\in\) Op\(_{?∩Y}\). Después existen B\(_{1}\), B\(_{2}\)\(\in\) Op con A\(_{1}\) = \(_{1}\)B Y y A\(_{2}\) = \(_{2}\)B Y. Pero luego \(_{1}\)A A\(_{2}\) = (\(_{1}\)B Y) (B\(_{2}\) Y) = (B\(_{1}\) B\(_{2}\)) Y, entonces es en Op\(_{?∩Y}\) desde B\(_{1}\) B\(_{2}\)\(\in\) Op.
La misma idea funciona para uniones arbitrarias: dado un conjunto I y A\(_{i}\) para cada \(\in\)i I, tenemos A\(_{i}\) = \(_{i}\)B Y para algunos B\(_{i}\) \(\in\)Op, y
\(\bigcup_{i \in I} A_{i}=\bigcup_{i \in I}\left(B_{i} \cap Y\right)=\left(\bigcup_{i \in i} B_{i}\right) \cap Y \in \mathbf{O p}_{? \cap Y}\)
Imaginemos una categoría V C, donde V es la quantale correspondiente a los conjuntos abiertos de un espacio topológico (X, Op). Su diagrama de Hasse sería un conjunto de puntos y algunas flechas entre ellos, cada uno etiquetado por un conjunto abierto U (\ subseteq\) Op. Podría verse algo como esto:
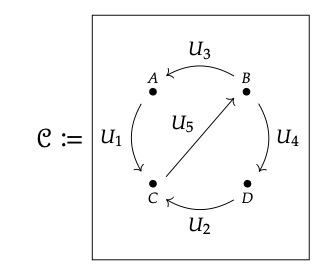
Recordemos de la Sección 2.3 que la 'distancia' entre dos puntos se calcula tomando la unión, sobre todos los caminos entre ellos, del producto monoidal de las distancias a lo largo de ese camino. Por ejemplo, C (B, C) = (U\(_{3}\)\(\land\) U\(_{1}\))\(\lor\) (U\(_{4}\)\(\land\) U\(_{2}\)), porque\(\land\) es el producto monoidal en V.
En general, podemos imaginar así el conjunto abierto C (a, b) como una especie de 'restricción de tamaño' para pasar de a a b, como puentes por los que su camión necesita pasar. La restricción de tamaño para llegar de a sí mismo es X: sin restricción. En general, para ir por cualquier ruta (sendero) dada de a a b, hay que encajar debajo de cada puente del camino, así que tomamos su encuentro. Pero podemos ir por cualquier camino, así que tomamos la unión sobre todos los caminos.
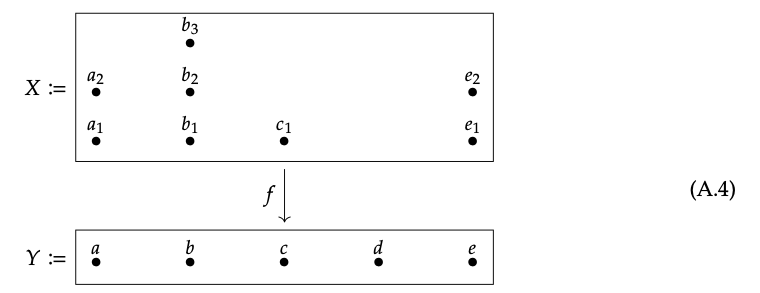
1. La fibra de f sobre a es {a\(_{1}\), a\(_{2}\)}.
2. La fibra de f sobre c es {c\(_{1}\)}.
3. La fibra de f sobre d es Ø.
4. A continuación se muestra una función f′: X → Y para la cual cada fibra tiene uno o dos elementos.
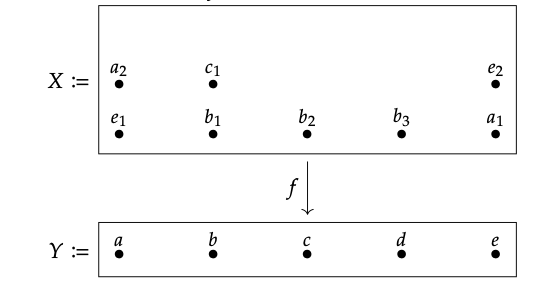
Consulte la Ec. (A.4).
1. Aquí hay un dibujo de las seis secciones sobre V\(_{1}\) = {a, b, c}:
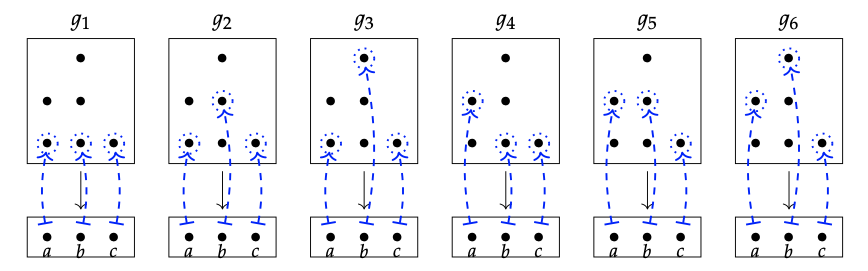
2. Cuando V\(_{2}\) = {a, b, c, d}, no hay secciones: Sec\(_{f}\) (V\(_{2}\)) = Ø.
3. Cuando V\(_{3}\) = {a, b, d, e}, el conjunto Sec\(_{f}\) (V\(_{3)\))) tiene 2 ∗ 3 ∗ 1 ∗ 2 = 12 elementos.
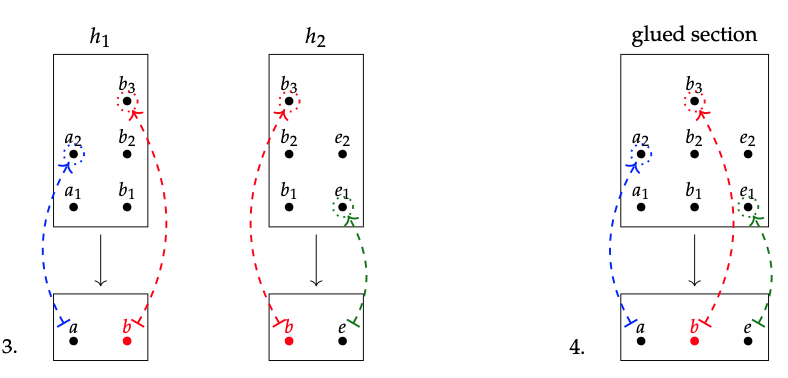
Sec\(_{f}\) ({a, b, c}) y Sec\(_{f}\) ({a, c}) se dibujan como la fila superior (conjunto de seis elementos) y la fila inferior (conjunto de dos elementos) a continuación, y el mapa de restricción también se muestra:
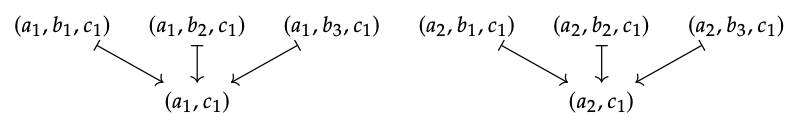
1. Dejar g\(_{1}\) := (a\(_{1}\), b\(_{1}\)) y g\(_{2}\) := (b\(_{2}\), e\(_{1}\)); estos no concuerdan en el solapamiento.
2. No, no hay sección g\(\in\) Sec\(_{f}\) (U\(_{1}\)\(\cup\) U\(_{2}\)) para la cual g |\(_{U_{2}\) = g\(_{1}\) y g |\(_{U_{2}\) = g\(_{2}\)
No, no existe una correspondencia uno a uno entre las poleas en M y los campos vectoriales en M. La relación entre las poleas en M y los campos vectoriales en M es que el conjunto de todos los campos vectoriales en M corresponde a una gavilla, es decir\(_{\pi}\), Sec, donde\(\pi\): TM → M es el haz tangente como se describe en el Ejemplo 7.46. Hay tantas poleas en M que ni siquiera forman un conjunto (es solo una 'colección'); nuevamente, un miembro de esta gigantesca colección es la gavilla Sec\(_{\pi}\) de todos los campos vectoriales posibles en M.
1. El diagrama de Hasse para la topología Sierpinsky es Ø → {1} → {1, 2}.
2. Un preheaf F on Op consiste en tres conjuntos cualesquiera y dos funciones cualesquiera F ({1, 2}) → F ({1}) → F (Ø) entre ellos.
3. Recordemos del Ejercicio 7.31 que la única cobertura no trivial (una cobertura de U no es trivial si no contiene U) ocurre cuando U = Ø en cuyo caso la familia vacía sobre U es una cobertura.
4. Como se explica en el Ejemplo 7.36, F será una gavilla iff F (Ø)\(\cong\) {1}. Así nosotros la categoría de poleas es equivalente a la de sólo dos conjuntos y una función F ({1, 2}) → F ({1}).
El espacio de un punto X = {1} tiene dos conjuntos abiertos, Ø y {1}, y cada gavilla S\(\in\) Shv (X) asigna S (Ø) = {()} por la condición de gavilla (ver Ejemplo 7.36). Entonces el único dato en una gavilla S\(\in\) Shv (X) es el conjunto S ({1}). Es así como obtenemos la correspondencia entre conjuntos y poleas en el espacio de un punto. De acuerdo con la Ec. (7.50), el clasificador de subobjeto Ω: Op (X)\(^{op}\) → Establecer en Shv (X) debe ser el functor donde Ω ({1}) es el conjunto de conjuntos abiertos de {1}. Así que estamos esperando ver que hay una correlación uno a uno entre el conjunto Op ({1}) y el conjunto\(\mathbb{B}\) = {verdadero, falso} de booleanos. En efecto hay: hay dos conjuntos abiertos de {1}, como dijimos, Ø y {1}, y estos corresponden a false y true respectivamente.
Por Eqs. (7.50) y (7.51) la definición de Ω (U) es Ω (U) := {U ′\(\in\) Op | U ′\(\subseteq\) U}, y la definición del mapa de restricción para V (\ subseteq\) U es U ′ → U ′ V.
1. Es funciontorial: dado W\(\subseteq\) V\(\subseteq\) U y U ′\(\subseteq\) U, efectivamente tenemos (U ′ V) W U ′ W, ya que W\(\subseteq\) V. Para la funcionalidad, también necesitamos la preservación de las identidades, y esto equivale a U ′ U = U ′ para todos los \(\subseteq\)U ′ U.
2. Sí, un presheaf es sólo un functor; la comprobación anterior es suficiente.
Necesitamos un homomorfismo gráfico de la siguiente forma:
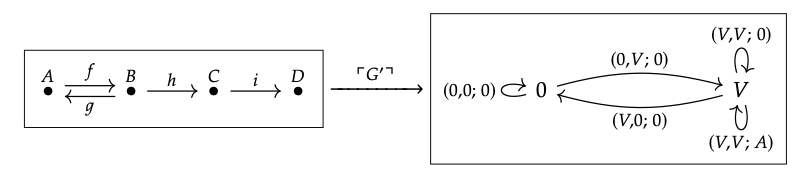
Sólo hay uno que clasifica G ′, y aquí está. Escribamos γ: =\(\lceil{G′}\rceil\).
- Como D falta de G ′, tenemos γ (D) = 0 (vértice: faltante).
- Dado que los vértices A, B, C están presentes en G ′ tenemos γ (A) = γ (B) = γ (C) = V (vértice: presente).
- Las fuerzas anteriores γ (i) = (V, 0; 0) (flecha desde el vértice presente hasta el vértice faltante: falta).
- Como la flecha f está en G ′, tenemos γ (f) = (V, V; A) (flecha desde el vértice presente hasta el vértice presente: presente).
- Dado que las flechas g y h faltan en G ′, tenemos γ (g) = γ (h) = (V, V; 0) (flecha desde el vértice presente hasta el vértice presente: falta).
Con U =\(\mathbb{R}\) − {0}\(\subseteq\)\(\mathbb{R}\), tenemos:
1. El complemento de U es\(\mathbb{R}\) − U {0} y ¬ U es su interior, que es ¬ U.
2. El complemento de ¬ U es\(\mathbb{R}\) −\(\mathbb{R}\), y esto es abierto, entonces ¬¬ U =\(\mathbb{R}\).
3. Es cierto que U\(\subseteq\) ¬¬ U.
4. Es falso que ¬¬ \(\subseteq\)\(^{?}\)U U.
1. Si para cualquier V\(\in\) Op tenemos\(\land\) V = V entonces cuando V = X tenemos\(\land\) X: = X = X, pero cualquier cosa que se cruce con X es en sí mismo, así que = X = X.
2. (\(\lor\)V) := (X\(\cup\) V) = X mantiene y (V ⇒ X)\(\bigcup_{\{R \in \mathbf{O p} \mid R \cap V \subseteq X\}} R=X\) sostiene porque (X V)\(\subseteq\) X.
3. Si para cualquier conjunto V\(\in\) Op tenemos (\(\lor\)V) = V, entonces cuando V = ∅ tenemos (\(\lor\)Ø) = (Ø) = Ø, pero cualquier cosa unionada con Ø es en sí misma, así que = Ø = Ø.
4. (\(\land\)V) = (Ø V) = Ø se mantiene, y (⇒ V) =\(\bigcup_{\{R \in \mathbf{O p} \mid R \cap Ø \subseteq X\}} R=X\) mantiene porque (X Ø)\(\subseteq\) V.
S es la gavilla de las personas, cuyo conjunto cambia con el tiempo: una sección en S en cualquier intervalo de tiempo es una persona que está viva a lo largo de ese intervalo. Una sección en el subobjeto {S | p} a lo largo de cualquier intervalo de tiempo es una persona que está viva y le gusta el clima a lo largo de ese intervalo de tiempo.
Necesitamos un ejemplo de un espacio X, una gavilla S\(\in\) Shv (X), y dos predicados p, q: S → Ω para los que se\(p(s) \vdash_{s: S} q(s)\) sostiene. Tomar X para ser el espacio de un punto, tomar S para ser la gavilla correspondiente al conjunto S =\(\mathbb{N}\), dejar que p (s) sea el predicado “24 ≤ s ≤ 28”, y dejar q (s) ser el predicado “s es no prime”. Entonces\(p(s) \vdash_{s: S} q(s)\) sostiene.
Como ejemplo informal, tomar X para ser la superficie de la tierra, tomar S para ser la gavilla de campos vectoriales como en el Ejemplo 7.46 pensado en términos de soplar viento. Que p sea el predicado “el viento sopla debido al este en algún lugar entre 2 y 5 kilómetros por hora” y que q sea el predicado “el viento sopla en algún lugar entre 1 y 5 kilómetros por hora”. Entonces\(p(s) \vdash_{s: S} q(s)\) sostiene. Esto significa que para cualquier conjunto abierto U, si el viento sopla hacia el este en algún lugar entre 2 y 5 kilómetros por hora en toda U, entonces el viento sopla en algún lugar entre 1 y 5 kilómetros por hora a lo largo de U también.
Tenemos el predicado p:\(\mathbb{N}\) ×\(\mathbb{Z}\) →\(\mathbb{B}\) dado por p (n, z) iff n ≤ | z |.
1. El predicado α (z: Z). p (n, z) se mantiene para {0}\(\subseteq\)\(\mathbb{N}\).
2. El predicado (z: Z). p (n, z) se mantiene para\(\mathbb{N}\)\(\subseteq\)\(\mathbb{N}\).
3. El predicado α (n: N). p (n, z) se sostiene para Ø\(\subseteq\)\(\mathbb{Z}\).
4. El predicado (n: N). p (n, z) se mantiene para\(\mathbb{Z}\)\(\subseteq\)\(\mathbb{Z}\).
Supongamos que s es una persona viva durante todo el intervalo U. Aplicar la definición anterior al ejemplo p (s, t) = “persona s está preocupada por noticias t” desde arriba.
1. La fórmula dice que a (t: T). p (s, t) “devuelve el conjunto abierto más grande V\(\subseteq\) U para el cual p (s |\(_{V}\), t) = V para todo \(\in\)t T (V).” Tenga en cuenta que T (V) es el conjunto de ítems que están en las noticias a lo largo del intervalo V. Sustituyendo, esto se convierte en “el mayor intervalo de tiempo V\(\subseteq\) U sobre el que la persona s está preocupada por las noticias t por cada elemento t que está en las noticias a lo largo de V”. Es decir, para que V no esté vacía, la persona s tendría que estar preocupada por cada elemento de noticias a lo largo de V. Mi conjetura es que hay un festival sucediendo o un gatito feliz en algún lugar que no le preocupa a esa persona, pero tal vez estoy asumiendo que esa persona es lo suficientemente “normal” mentalmente. Puede haber gente que a veces esté preocupada por literalmente todo en las noticias; le pedimos que por favor sea amable con ellos.
2. Sí, es exactamente la misma descripción.
Supongamos que s es una persona viva durante todo el intervalo U. Aplicar la definición anterior al ejemplo p (s, t) = “persona s está preocupada por noticias t” desde arriba.
1. La fórmula dice que (t: T). p (s, t) “devuelve la unión V =\(\bigcup_{i}\) V\(_{i}\) de todos los conjuntos abiertos V\(_{i}\) para los que existe alguna t\(_{i}\)\(\in\) T (V\(_{i}\)) satisfaciendo p (s |\(_{V_{i}}\), t\(_{i}\)) = V\(_{i}\).” Sustituyendo, esto se convierte en “la unión de todos los intervalos de tiempo V\(_{i}\) por lo que hay algún ítem t i en las noticias sobre el cual s está preocupado a lo largo de V”\(_{i}\). En otras palabras, es todo el tiempo que s está preocupado por al menos una cosa en las noticias. Quizás cuando s está durmiendo o concentrándose en algo, no le preocupa nada, en cuyo caso los intervalos de dormir o concentrarse no serían subconjuntos de V. Pero si se dice “ha habido una serie de malas noticias el año pasado, es como si siempre me preocupara algo! ”, dice que es como V = “el año pasado”.
2. Esto parece algo bueno porque “existe una noticia que preocupa s” significa: se permite que la noticia misma cambie mientras la preocupación de la persona permanezca. Alguien podría estar en desacuerdo y pensar que el predicado debería significar “hay una noticia que preocupa s a lo largo de todo el intervalo V”. En ese caso, tal vez esta persona esté trabajando dentro de un topos diferente, por ejemplo, uno donde el sitio tenga menos coberturas. En efecto, es la noción de cobertura la que hace que la cuantificación existencial funcione de la manera en que lo hace.
Es claro que si j (j (q)) = j (q) entonces j (j (q)) ≤ j (q) por reflexividad. Por otro lado, supongamos la hipótesis, que p ≤ j (p) para todos U\(\subseteq\) X y p\(\in\) Ω (U). Si j (j (q)) ≤ j (q), entonces dejando p: = j (q) tenemos tanto j (p) ≤ p como p ≤ j (p). Esto significa p\(\cong\) j (p), pero Ω es un poset (no solo un preorden) así que p = j (p), es decir j (j (q)) = j (q) como se desee.
Que S sea la gavilla de la gente y j sea “asumiendo que Bob está en San Diego...”
1. Toma p (s) para ser “s le gusta el clima”.
2. Que U sea el intervalo 2019/01/01—2019/02/01. Para una persona arbitraria \(\in\)S (U), p (s) es un subconjunto de U, y significa el subconjunto de U a lo largo del cual s le gusta el clima.
3. Del mismo modo j (p (s)) es un subconjunto de U, y significa el subconjunto de U a lo largo del cual, asumiendo que Bob está en San Diego, s le gustó el clima. En otras palabras, j (p (s)) es cierto siempre que Bob no está en San Diego, y es cierto cuando a s le gusta el clima.
4. Es cierto que p (s) ≤ j (p (s)), por el 'en otras palabras' anterior.
5. Es cierto que j (j (p (s)) = j (p (s), porque supongamos dado un tiempo durante el cual “si Bob está en SanDiego entonces si Bob está en San Diego entonces a s le gusta el clima”. Entonces si Bob está en San Diego durante este tiempo entonces s le gusta el clima. Pero eso es exactamente lo que significa j (p (s)).
6. Toma q (s) para ser “s es feliz”. Supongamos que “si Bob está en SanDiego entonces a ambos les gusta el clima y s es feliz”. Entonces tanto “si Bob está en San Diego entonces a s le gusta el clima” como “si Bob está en San Diego entonces s es feliz” también son ciertas. Lo inverso es igualmente claro.
Tenemos o\(_{[a, b]}\) := {[d, u]\(\in\)\(\mathbb{I}\)\(\mathbb{R}\) | a < d ≤ u < b}.
1. Desde 0 ≤ 2 ≤ 6 ≤ 8, tenemos [2, 6]\(\in\) o\(_{[0, 8]}\) por la fórmula anterior.
2. Para tener [2, 6]\(\in\)\(^{?}\) o o\(_{[0, 5]}\)\(_{[4, 8]}\), necesitaríamos tener ya sea [2,6]\(_{[0, 5]}\) o\(\in\)\(^{?}\) o [2,6]\(\in\)\(^{?}\) o\(_{[4, 8]}\). Pero la fórmula no se sostiene en ninguno de los dos casos.
Un subconjunto U\(\subseteq\)\(\mathbb{R}\) está abierto en la topología subespacial de\(\mathbb{R}\)\(\subseteq\)\(\mathbb{I}\)\(\mathbb{R}\) iff hay un conjunto abierto U ′\(\subseteq\)\(\mathbb{I}\)\(\mathbb{R}\) con U =b U ′\(\mathbb{R}\). Queremos mostrar que este es el caso iff U está abierto en la topología habitual. Supongamos que U está abierto en la topología subespacial. Entonces U = U ′\(\mathbb{R}\), donde U ′\(\subseteq\)\(\mathbb{I}\)\(\mathbb{R}\) es la unión de algunos basicopenos, U ′ =\(\bigcup)_{i \in I}\) o\(_{[a_{i}, b_{i}]}\), donde o\(_{[a_{i}, b_{i}]}\) = {[d, u]\(\in\) \(\mathbb{I}\)\(\mathbb{R}\)| a\(_{i}\) < d < u < b\(_{i}\)}. Dado que\(\mathbb{R}\) = {[x, x]\(\in\)\(\mathbb{I}\)\(\mathbb{R}\)}, la intersección U ′\(\mathbb{R}\) será entonces
\(U=\bigcup_{i \in I}\left\{x \in \mathbb{R} \mid a_{i}<x<b_{i}\right\}\)
y esto es solo la unión de bolas abiertas B (m\(_{i}\), r\(_{i}\)) donde\(m_{i}:=\frac{a_{i}+b_{i}}{2}\) está el punto medio y\(r_{i}:=\frac{b_{i}-a_{i}}{2}\) es el radio del intervalo (a\(_{i}\), b\(_{i}\)). Las bolas abiertas B (m\(_{i}\), r\(_{i}\)) están abiertas en la topología habitual\(\mathbb{R}\) y la unión de aperturas es abierta, por lo que U está abierta en la topología habitual. Supongamos que U está abierto en la topología habitual.
Entonces U =\(\bigcup)_{j \in J}\) B (m\(_{j}\),\(\mathcal{E}\)\(_{j}\)) para algún conjunto J. Dejar a\(_{j}\) := m\(_{j}\) −\(\mathcal{E}\)\(_{j}\) y b\(_{j}\) := m\(_{j}\) +\(\mathcal{E}\)\(_{j}\). Entonces
\(U=\bigcup_{j \in J}\left\{x \in \mathbb{R} \mid a_{j}<x<b_{j}\right\}=\bigcup_{j \in J}\left(o_{\left[a_{j}, b_{j}\right]} \cap \mathbb{R}\right)=\left(\bigcup_{j \in J} o_{\left[a_{j}, b_{j}\right]}\right) \cap \mathbb{R}\)
que está abierto en la topología subespacial.
Arreglar cualquier espacio topológico (X, Op\(_{X}\)) y cualquier subconjunto R\(\subseteq\)\(\mathbb{I}\)\(\mathbb{R}\) del dominio de intervalo. Definir H\(_{X}\) (U) := {f: U R → X | f es continuo}.
1. H\(_{X}\) es un preheaf: dado V\(\subseteq\) U el mapa de restricción envía la función continua f: U R → X a su restricción a lo largo del subconjunto V R\(\subseteq\) U R.
2. Se trata de una gavilla: dada cualquier familia U\(_{i}\) de conjuntos abiertos con \(\bigcup_{i}\)U = U\(_{i}\) y una función continua f\(_{i}\): \(_{i}\)U R → X por cada i, acordando superposiciones, se pueden pegar entre sí para dar una función continuasobre todos los U R, ya que U R = (U) R =\(\bigcup_{i}\) U (U\(_{i}\)) R =\(\bigcup_{i}\) U\(_{i}\) (U \(_{i}\)R).


