8.6: Soluciones para Chapter6
- Page ID
- 112219
Deje A = {a, b}, y considere los pedidos por adelantado que se muestran aquí:\(\begin{array}{l} a \\ \bullet \end{array}\)\(\begin{array}{l} b \\ \bullet \end{array}\),\(\begin{array}{l} a \\ \bullet \end{array}\) →\(\begin{array}{l} b \\ \bullet \end{array}\),\(\begin{array}{l} a \\ \bullet \end{array}\)\(\leftrightarrows\)\(\begin{array}{l} b \\ \bullet \end{array}\).
- El más a la izquierda (el preorden discreto en A) no tiene ningún objeto inicial, porque a\(nleq\) b y b\(nleq\) a.
- El del medio tiene un objeto inicial, a saber, a.
- El más a la derecha (el preorden co-discreto en A) tiene dos objetos iniciales.
Recordemos que los objetos de una categoría libre en una gráfica son los vértices de la gráfica, y los morfismos son caminos. Así, la categoría libre en una gráfica G tiene un objeto inicial si existe un vértice v que tiene una ruta única a cada objeto. En 1. y 2., el vértice a tiene esta propiedad, por lo que las categorías libres en las gráficas 1. y 2. tienen objetos iniciales. En la gráfica 3., ni a ni b tienen un camino entre sí, y así no hay objeto inicial. En la gráfica 4., el vértice a tiene muchos caminos hacia sí mismo, y de ahí su categoría libre tampoco tiene un objeto inicial.
1. Las condiciones restantes son que f (1\(_{R}\)) = 1\(_{S}\), y que f (r 1 ∗\(_{R}\) r 2) = f (r 1) ∗\(_{S}\) f (r 2).
2. El objeto inicial en la categoría Rig es el rig de números naturales (\(\mathbb{N}\), 0, +, 1, ∗).
El hecho de que sea inicial significa que para cualquier otro rig R = (R, 0\(_{R}\)\(_{R}\), +\(_{R}\), 1, ∗\(_{R}\)), existe un homomorfismo único de rig f:\(\mathbb{N}\) → R.
¿Qué es este homomorfismo? Bueno, para ser un homomorfismo de plataforma, f debe enviar 0 a 0\(_{R}\), 1 a 1\(_{R}\). Además, también debemos tener f (m + n) = f (m) +\(_{R}\) f (n), y por lo tanto
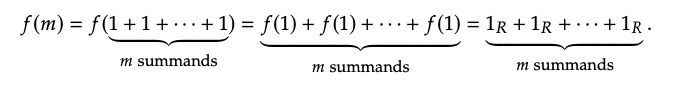
Entonces, si hay un aparejo homomorfismo f:\(\mathbb{N}\) → R, debe ser dado por la fórmula anterior. Pero, ¿esta fórmula funciona correctamente para la multiplicación?
Queda por verificar f (m ∗ n) = f (m) ∗\(_{R}\) f (n), y esto seguirá de la distributividad. Observando que f (m ∗ n) es igual a la suma de m n copias de 1\(_{R}\), tenemos

Así (\(\mathbb{N}\), 0, +, 1, ∗) es el objeto inicial en Rig.
En la Definición 6.1, es el objeto inicial Ø\(\in\) C el que es universal. En este caso, todos los objetos c\(\in\) C son 'objetos comparables'. Entonces la propiedad universal del objeto inicial es que a cualquier objeto c\(\in\) C, hay un mapa único Ø → c proveniente del objeto inicial.
Si c\(_{1}\) es inicial entonces por la propiedad universal, para cualquier c hay un morfismo único c\(_{1}\) → c; en particular, hay un morfismo único c\(_{1}\) → c\(_{2}\), llámalo f. De igual manera, si c\(_{2}\) es inicial entonces hay un morfismo único c\(_{2}\) → c\(_{1}\), llámalo g. Pero, ¿cómo sabemos que f y g son mutuamente inversos? Pues ya que c\(_{1}\) es inicial hay un morfismo único c\(_{1}\) →\(_{1}\) c. Pero podemos pensar en dos: id c 1 y f; g. Por lo tanto, deben ser iguales. De manera similar para c\(_{2}\), entonces tenemos f; g = id\(_{c_{1}}\) y g; f = id\(_{c_{2}}\), que es la definición de f y g siendo mutuamente inversas.
Sea (P, ≤) un preorden, y p, q\(\in\) P. Recordemos que un preorden es una categoría con como máximo un morfismo, denotado ≤, entre dos objetos cualesquiera. También recordemos que todos los diagramas en un preorden conmutan, ya que esto significa que dos morfismos cualesquiera con el mismo dominio y codominio son iguales.
Traduciendo la Definición 6.11 a este caso, un coproducto p + q es P es un elemento de P tal que p ≤ p + q y q ≤ p + q, y tal que para todos los elementos x\(\in\) P con mapas p ≤ x y q ≤ x, tenemos p + q ≤ x. Pero esto dice exactamente que p + q es una unión: es un elemento mínimo por encima tanto de p como de q. Así, los coproductos en preordenes son exactamente los mismos que se unen.
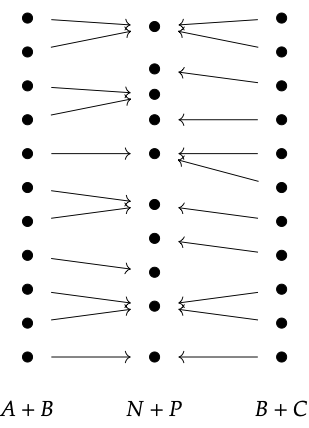
La función [f, g] se define por
[f, g]: A B\(\longrightarrow\) T
manzana1\(\mapsto\) a
banana1\(\mapsto\) b
pera1\(\mapsto\) p
cereza1\(\mapsto\) c
naranja1\(\mapsto\) o
manzana2\(\mapsto\) e
tomate2\(\mapsto\) o
mango2\(\mapsto\) o.
1. La ecuación ι\(_{A}\); [f, g] = f es la conmutatividad del triángulo izquierdo en el diagrama conmutativo (6.12) definiendo [f, g].
2. La ecuación ι\(_{B}\); [f, g] = g es la conmutatividad del triángulo derecho en el diagrama conmutativo (6.12) definiendo [f, g].
3. La ecuación [f, g]; h = [f; h, g; h] se desprende de la propiedad universal del coproducto. En efecto, el diagrama
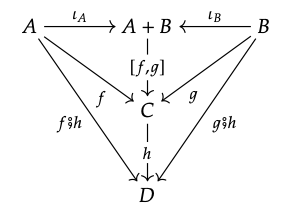
conmuta, y la propiedad universal dice que hay un mapa único [f; h, g; h]: A + B → D para el que esto ocurre.
De ahí que debemos tener [f, g]; h = [f; h, g; h]. 4. Del mismo modo, para mostrar [ι\(_{A}\), ι\(_{B}\)] = id\(_{A + B}\), observe que el diagrama
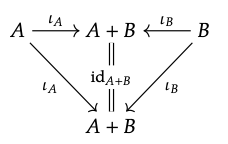
trivialmente conmuta. De ahí por la singularidad en (6.12), [ι\(_{A}\), ι\(_{B}\)] = id\(_{A + B}\).
Este ejercicio trata de mostrar que los coproductos y un objeto inicial dan una categoría monoidal simétrica. Como todo lo que tenemos son coproductos y un objeto inicial, y dado que estos están definidos por sus propiedades universales, la solución es utilizar estas propiedades universales una y otra vez, para demostrar que todos los datos de la Definición 4.45 pueden ser construidos.
1. Para definir un functor +: C × C → C debemos definir su acción sobre objetos y morfismos. En ambos casos, solo tomamos el coproducto. Si (A, B) es un objeto de C × C, su imagen A + B es, como de costumbre, el coproducto de los dos objetos de C.
Si (f, g): (A, B) → (C, D) es un morfismo, entonces podemos formar un morfismo f + g = [f; ι\(_{C}\), g; ι\(_{D}\)]: A + B → C + D, donde ι\(_{C}\): C → C + D y ι\(_{D}\): D → C + D son los morfismos canónicos dados por la definición del coproducto A + B.
Obsérvese que esta construcción envía morfismos de identidad a morfismos de identidad, ya que por el Ejercicio 6.17 4 tenemos
id\(_{A}\) + id\(_{B}\) = [id\(_{A}\); ι\(_{A}\), id\(_{B}\); ι\(_{B}\)] = [ι\(_{A}\), ι\(_{B}\)] = id\(_{A + B}\).
Para demostrar que + es un functor, necesitamos mostrar también que conserva la composición. Supongamos que también tenemos amorfismo (h, k): (C, D) → (E, F) en C × C. Necesitamos mostrar que (f + g); (h + k) = (f; h) + (g ; k). Se trata de una versión un poco más complicada del argumento en el Ejercicio 6.17 3. Se deduce del hecho de que el siguiente diagrama conmuta:
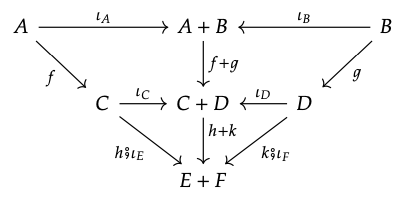
De hecho, nuevamente utilizamos la singularidad del copaireo en (6.12), esta vez para mostrar que (f; h) + (g; k) = [f; h; ι\(_{E}\), k; ι\(_{F}\)] = (f + g ); (h + k), según se requiera.
2. Recordemos la propiedad universal del objeto inicial da un mapa único! \(_{A}\): Ø → A. Entonces el copaireo [id\(_{A}\),! \(_{A}\)] es un mapa A + Ø → A. Además, se trata de un isomorfismo con inverso i\(_{A}\): A → A + Ø.
En efecto, utilizando las propiedades del Ejercicio 6.17 y la propiedad universal del objeto inicial, tenemos ι\(_{A}\); [id\(_{A}\),! \(_{A}\)] = id\(_{A}\), y
[id\(_{A}\),! \(_{A}\)]; ι\(_{A}\) = [id\(_{A}\); ι\(_{A}\),! \(_{A}\); ι\(_{A}\)] = [ι\(_{A}\),! \(_{A + Ø}\)] = [ι\(_{A}\), ι\(_{Ø}\)] = id\(_{A + Ø}\).
Un argumento análogo muestra [! \(_{A}\), id\(_{A}\)]: Ø + A → A es un isomorfismo.
3. Simplemente anotaremos los mapas y sus inversos; te dejamos a ti, si quieres, que compruebes que efectivamente son inversos
a) El mapa [id\(_{A + ι_{B},ι_{C}}\)] = [[ι\(_{A}\), ι\(_{B}\); ι\(_{B + C}\)], ι\(_{C}\); ι\(_{B + C}\)]: (A + B) + C → A + (B + C) es un isomorfismo, con inversa [ι\(_{A}\), ι\(_{B}\) + id\(_{C}\)]: A + (B + C) → (A + B) + C.
b) El mapa [ι\(_{A}\), ι\(_{B}\)]: A + B → B + A es un isomorfismo.
Tenga en cuenta que nuestra notación aquí es un poco confusa: hay dos mapas llamados ι\(_{A}\), (i) ι\(_{A}\): A → A + B, y (ii) ι\(_{A}\): A → B + A, y de manera similar para ι\(_{B}\). En lo anterior nos referimos al mapa (ii). Tiene inversa [ι\(_{A}\), ι\(_{B}\)]: B + A → A + B, donde en este caso nos referimos al mapa (i).
1. Supongamos que se le da un diagrama arbitrario de la forma B ← A → C en Disco\(_{S}\); necesitamos demostrar que tiene un pushout. Los únicos morfismos en Disco\(_{S}\) son las identidades, por lo que en particular A = B = C, y el cuadrado que consiste en todas las identidades es su pushout.
2. Supongamos que Disc\(_{S}\) tiene un objeto inicial s. ¡Entonces S no puede estar vacía! Pero tampoco puede tener más de un objeto, porque si s ′ es otro objeto entonces hay un morfismo s → s ′, pero los únicos morfismos en S son identidades así que s = s ′. De ahí que el conjunto S debe constar exactamente de un elemento.
El pushout es el conjunto\(\underline{4}\), como se representa en la parte superior derecha en el diagrama de abajo, equipado también con las funciones representadas:
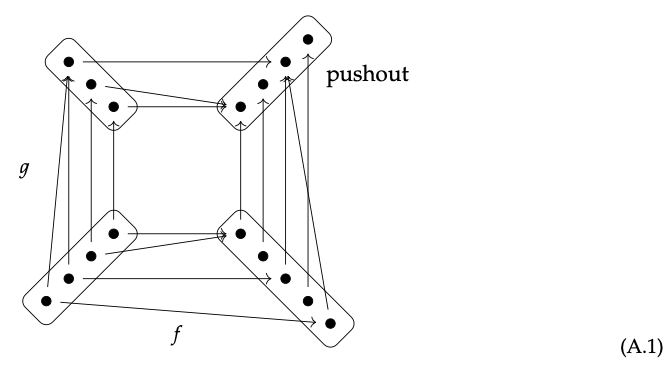
Queremos ver que esto se comprueba con la descripción del Ejemplo 6.25, es decir, que es el conjunto de clases de equivalencia\(\underline{5}\) en 3 generado por la relación {f (a) ∼ g (a) | a\(\in\)\(\underline{4}\)}. Si denotamos elementos de 5 como {1,..., 5} y los de\(\underline{3}\) como {1′, 2′, 3′}, podemos redibujar las funciones f, g:
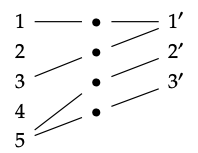
que dice tomamos la relación de equivalencia en\(\underline{5}\)\(\underline{3}\) generada por: 1 ∼ 1′,, 3 ∼ 1′, 5 ∼ 2′, y 5 ∼ 3′. Las clases de equivalencia son {1, 1′, 3}, {2}, {4} y {5, 2′, 3′}. Estos cuatro son exactamente los cuatro elementos del conjunto etiquetados como 'pushout' en la Ec. (A.1).
1. El diagrama a la izquierda conmuta porque Ø es inicial, y así tiene un mapa único Ø → X + Y. Esto implica que debemos tener f; ι\(_{X}\) = g; ι\(_{Y}\).
2. Existe un mapa único X + Y → T que hace que el diagrama en (6.21) desplazamientos implique por la propiedad universal del coproducto (6.12) aplicado a los mapas x: X → T e y: Y → T.
3. Supongamos que X +\(_{Ø}\) Y existe. Por la propiedad universal de Ø, dado cualquier par de flechas x: X → T e y: Y → T, el diagrama
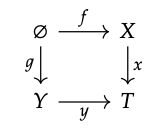
desplazamientos. Esto quiere decir, por la propiedad universal del pushout X +\(_{Ø}\) Y, existe un mapa único t: X +\(_{Ø}\) Y → T tal que ι\(_{X}\); t = x y ι\(_{Y}\); t = y.
Así X +\(_{Ø}\) Y es el coproducto X + Y.
Tenemos que verificar que el colimit del diagrama que se muestra a la izquierda realmente se da tomando tres pushouts como se muestra a la derecha:

Es decir, necesitamos mostrar que S, junto con los mapas de A, B, X, Y y Z, tiene la propiedad universal requerida. Así que supongamos dado un objeto T con dos diagramas de desplazamiento como se muestra:
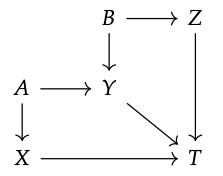
Tenemos que mostrar que hay un mapa único S → T haciendo que todo viaje. Como Q es un pushout de X ← A → Y, hay un mapa único Q → T haciendo un triángulo conmutativo con Y, y como R es el pushout de Y ← B → Z, hay un mapa único R → T haciendo un triángulo conmutativo con Y. Esto implica que hay un cuadrado de desplazamiento (Y, Q, R, T), y de ahí un mapa único S → T de su pushout haciendo que todo se conmute. Esto es lo que queríamos mostrar.
La fórmula en el Teorema 6.37 dice que el pushout X +\(_{N}\) Y viene dado por el conjunto de clases de equivalencia de X N Y bajo la relación de equivalencia generada por x ∼ n si x = f (n), e y ∼ n si y (n), donde x\(\in\) X, y\(\in\) Y, n\(\in\) N. Ya que por cada \(\in\)n N existe una x\(\in\) X tal que x = f (n), este conjunto es igual al conjunto de clases de equivalencia de X Y bajo la relación de equivalencia generado por x ∼ y si existe n tal que x = f (n) e y = g (n). Esta es exactamente la descripción del Ejemplo 6.25.
El producto monoidal es
Que x e y sean cospanes componibles en Cospan\(_{FinSet}\). En términos de cables y componentes conectados, la regla de composición en Cospan\(_{FinSet}\) dice que (i) el cospan compuesto tiene un elemento único en el ápice para cada componente conectado de la concatenación de los diagramas de cables x e y, y (ii) en el cable diagrama para x; y, cada elemento de los pies está conectado por un cable al elemento que representa el componente conectado al que pertenece.
Los morfismos 1, 4 y 6 son iguales, y los morfismos 3 y 5 son iguales. El morfismo 3 no es igual a ningún otro morfismo representado. Esta es una consecuencia inmediata del Teorema 6.55.
- La entrada a h debe estar etiquetada como B.
- La salida de g debe etiquetarse D, ya que sabemos por las etiquetas en la parte superior derecha que h es un morfismo B → D D.
- ¡El cuarto cable de salida del compuesto también debe estar etiquetado como D!
Dibujamos las representaciones de funciones arriba, y las representaciones de cableado a continuación. Tenga en cuenta que representamos el conjunto vacío con espacio en blanco.
La ley especial dice que el compuesto de cospans
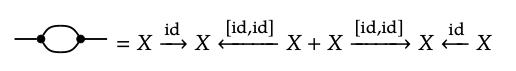
es la identidad. Esto se reduce a comprobar que la plaza

es un cuadrado de pushout. Es trivial ver que la plaza conmuta. Supongamos ahora que tenemos mapas f: X → Y y g: X → Y tal que
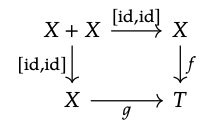
Escribe\(_{1}\): X → X + X para el mapa en la primera copia de X en X + X, dada por la definición de coproducto. Entonces, usando el hecho de que ι\(_{1}\); [id, id] = id del Ejercicio 6.17 1, y la conmutatividad del cuadrado anterior, tenemos f = ι\(_{1}\); [id, id]; f = ι\(_{1}\); [id, id]; g = g. Esto quiere decir que f: X → T es el mapa único tal que
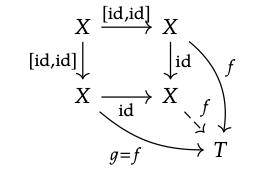
viaja, y por lo tanto (A.2) es un cuadrado pushout.
El diagrama que falta es
Deje que A\(\subseteq\) S y B\(\subseteq\) T. Entonces
\ (\ begin {alineado}
\ varphi_ {S^ {\ prime}, T^ {\ prime}}\ izquierda (\ left (\ mathrm {im} _ {f}\ veces\ mathrm {im} _ {g}\ derecha) (A\ veces B)\ derecha) &=\ varphi_ {S^ {\ prime}, T^ {\ prime}} (\ {f (a)\ mediados a\ en A\}\ veces\ {g (b)\ mediados b\ en B\})\\
&=\ {(f (a), g (b))\ mediados a\ en A, b\ en B\}\\
& amp; =\ nombreoperador {im} _ {f\ veces g} (A\ veces B)\\
&=\ nombreoperador {im} _ {f\ veces g}\ left (\ varphi_ {S, T} (A, B)\ derecha)
\ end {alineado}\)
Así los desplazamientos cuadrados requeridos.
Significan que cada categoría Cospan\(_{C}\) es igual a una categoría Cospan\(_{F}\), para algunos F bien elegidos. También te dicen cómo elegir esta F: tomar el functor F: C → Set que envía cada objeto de C al conjunto {∗}, y cada morfismo de C a la función de identidad en {∗}. Por supuesto, habrá que comprobar que este functor es un functor monoidal simétrico laxo, pero de hecho esto no es difícil de hacer.
Para comprobar que Cospan\(_{C}\) es igual a Cospan\(_{F}\), primero observe que tienen los mismos objetos: los objetos de C. A continuación, observe que un morfismo en Cospan\(_{F}\) es un cospan X ← N → Y en C junto con un elemento de FN = {∗}. Pero FN también tiene un elemento único, ∗! Entonces no hay otra opción aquí, y podemos considerar los morfismos de Cospan\(_{F}\) solo para ser cospans en C.
Además, la composición de los morfismos en Cospan\(_{F}\) es simplemente la composición habitual de los cospanes vía pushout, por lo que Cospan\(_{F}\) = Cospan\(_{C}\).
(Más técnicamente, podríamos decir que Cospan\(_{C}\) y Cospan\(_{F}\) son isomórficos, donde el isomorfismo es el funtor de identidad sobre objetos Cospan\(_{C}\) → Cospan\(_{F}\) que simplemente decora cada cospan con ∗, y su inverso es el que olvida esto ∗. Pero esto está lo suficientemente cerca como para igualar a que muchos teóricos de categoría, nosotros incluidos, no les importa decir igual en este caso).
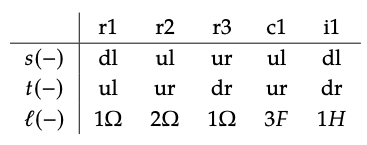
Podemos representar el circuito en la Ec. (6.71) por la tupla (V, A, s, t, l) donde V = {ul, ur, dl, dr}, A = {r1, r2, r3, c1, i1}, y s, t, y l están definidos por la tabla
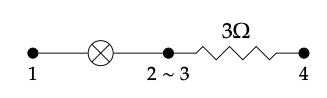
El circuito Circ (f) (c) es
El circuito ψ\(_{\underline{2, 2}}\) (b, s) es la unión disjunta de las dos gráficas etiquetadas b y s:

El cospan es el cospan\(\underline{1} \stackrel{f}{\rightarrow} \underline{2} \stackrel{g}{\leftarrow} \underline{1}\), donde f (1) y g (1) = 2. La decoración es el C-ciruit (\(\underline{2}\), {a}, s, t, l), donde s (a) = 1, t (a) = 2 y l (a) = batería.
Recordemos el circuito C = (V, A, s, t, l) de la solución al Ejercicio 6.79. Entonces el primer cospan decorado viene dado por el cospan\(\underline{1} \stackrel{f}{\rightarrow} V \stackrel{g}{\leftarrow} \underline{2}\), f (1) = ul, (1) = ur, y g (2) = ur, decorado por el circuito C. El segundo cospan decorado viene dado por el cospan\(\underline{1} \stackrel{f'}{\rightarrow} V' \stackrel{g'}{\leftarrow} \underline{2}\) y el circuito C′: = (V ′, A′, s ′, t ′, l′), donde V ′ = {l, r, d}, A ′ = {r1′, r2′}, y las funciones están dadas por las tablas
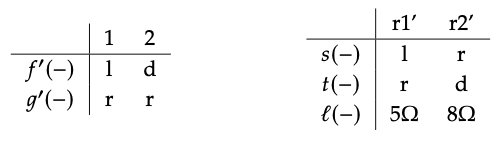
Para componer estos, primero tomamos el pushout de\(V \stackrel{g}{\leftarrow} \underline{2} \stackrel{f'}{\leftarrow} V'\).
Esto da el nuevo ápice V ′′ = {ul, dl, dr, m, r} con cinco elementos, y cospan compuesto\(\underline{1} \stackrel{h}{\rightarrow} V'' \stackrel{k}{\leftarrow} \underline{2}\) dado por h (1) = ul, k (1) = r y k (2) = m. El nuevo circuito viene dado por (V, ′′ A + A ′, s, ′′ t, ′′ l′′) donde las funciones están dadas por
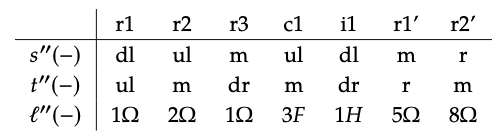
Esto es exactamente lo que se representa en la Ec. (6.74).
Componiendo η y x tenemos
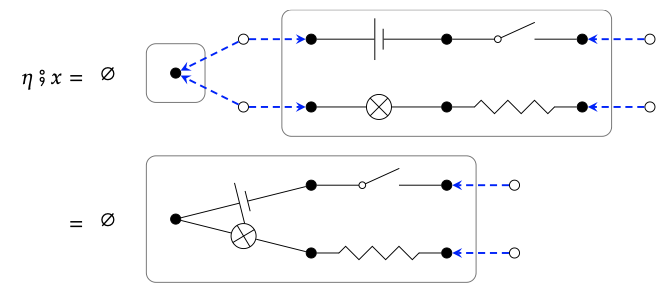
y componiendo el resultado de\(\mathcal{E}\) da
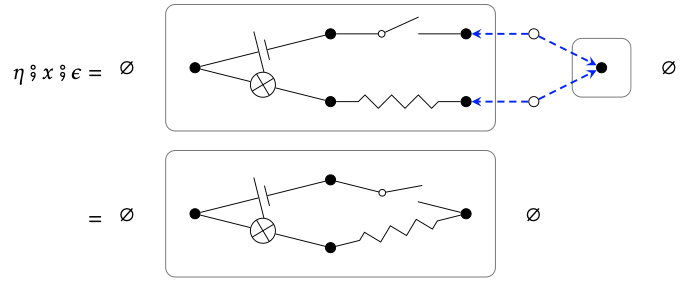
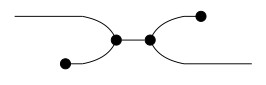
1. El cospan que se muestra a la izquierda corresponde al diagrama de cableado mostrado a la derecha:
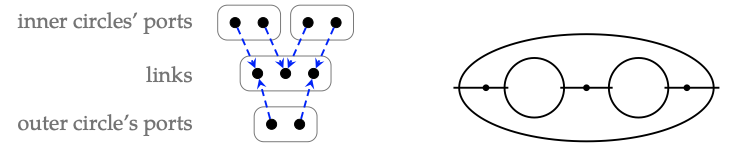
Tiene dos círculos internos, cada uno con dos puertos. Un puerto del primero está cableado a un puerto del segundo. Un puerto del primero está cableado al círculo exterior, y un puerto del segundo está cableado al círculo exterior. Esto es exactamente lo que dice hacer el cospan.
2. El cospan que se muestra a la izquierda corresponde al diagrama de cableado mostrado a la derecha:
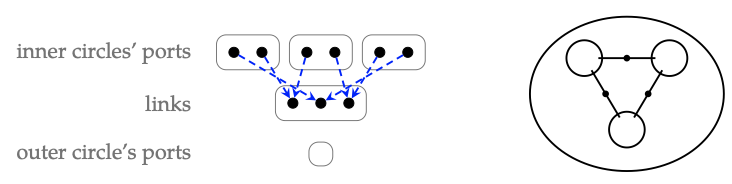
3. El compuesto g ◦\(_{1}\) f tiene arity (2, 2, 2, 2; 0); hay una representación a la izquierda:
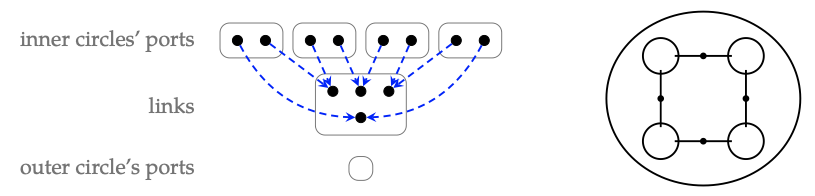
4. El diagrama de cableado asociado se muestra a la derecha arriba. Se puede ver que un diagrama ha sido sustituido por un círculo del otro.


