Saltar al contenido principal
LibreTexts Español

1.1: Números enteros

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    116286

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje

    • conocer la diferencia entre números y números
    • saber por qué nuestro sistema de números se llama el sistema de numeración hinduo-árabe
    • entender el sistema de número posicional base diez
    • ser capaz de identificar y graficar el número entero

    Números y Números

    Comenzamos nuestro estudio de las matemáticas introductorias examinando su bloque de construcción más básico, el número.

    Definición: Número

    Un número es un concepto. Sólo existe en la mente.

    El concepto más antiguo de un número fue un pensamiento que permitía a las personas imaginarse mentalmente el tamaño de alguna colección de objetos. Para anotar el número que se está conceptualizando, se utiliza un numeral.

    Definición: Numeral

    Un numeral es un símbolo que representa un número.

    En uso común hoy en día no distinguimos entre un número y un número. En nuestro estudio de las matemáticas introductorias, seguiremos este uso común.

    Conjunto de Muestras A

    Los siguientes son números. En cada caso, el primero representa el número cuatro, el segundo representa el número ciento veintitrés, y el tercero, el número mil cinco. Estos números se representan de diferentes maneras.

    • Números hindu-arábigos
      4, 123, 1005
    • Números romanos
      IV, CXXIII, MV
    • Números egipcios:

    Tres diagramas en sucesión, cada uno con una etiqueta abajo. Tres líneas verticales cortas, trazos etiquetados. Una línea arremolinada junto a dos líneas en forma de herradura, junto a tres líneas verticales cortas, etiquetadas como cuerda enrollada, huesos del talón y trazos. Un dibujo en forma de flor junto a cinco líneas verticales, etiquetadas, flor de loto y trazos.

    Conjunto de práctica A

    ¿Las frases “cuatro”, “ciento veintitrés” y “mil cinco” califican como números? ¿Sí o no?

    Contestar

    Sí. Las letras son símbolos. Tomados como colección (una palabra escrita), representan un número.

    El Sistema de Numeración Hindu-Árabe

    Definición: Sistema de Numeración Hindu-Árabe

    Nuestra sociedad utiliza el sistema de numeración Hindu-Árabe. Este sistema de numeración comenzó poco antes del siglo III cuando los hindúes inventaron los números

    0 1 2 3 4 5 6 7 8 9

    Definición: Lenoardo Fibonacci

    Alrededor de mil años después, en el siglo XIII, un matemático llamado Leonardo Fibonacci de Pisa introdujo el sistema en Europa. Entonces fue popularizado por los árabes. Así, el nombre, sistema de numeración hindu-árabe.

    El Sistema de Número Posicional Base Diez

    Definición: Dígitos

    Los números hindu-arábigos 0 1 2 3 4 5 6 7 8 9 se denominan dígitos. Podemos formar cualquier número en el sistema numérico seleccionando uno o más dígitos y colocándolos en ciertas posiciones. Cada posición tiene un valor particular. El matemático hindú que ideó el sistema alrededor del 500 d.C. afirmó que “de un lugar a otro cada uno es diez veces lo anterior”.

    Definición: Base Diez Sistemas Posicionales

    Es por esta razón que nuestro sistema numérico se llama sistema de números posicionales con base diez.

    Definición: Comas

    Cuando los números están compuestos por más de tres dígitos, a veces se utilizan comas para separar los dígitos en grupos de tres.

    Definición: Periodos

    A estos grupos de tres se les llama periodos y simplifican enormemente la lectura de números.

    En el sistema de numeración Hindu-Árabe, un periodo tiene un valor asignado a cada una o sus tres posiciones, y los valores son los mismos para cada periodo. Los valores de posición son

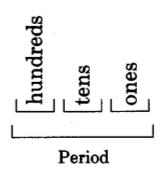
    Tres segmentos, etiquetados de izquierda a derecha, cientos, decenas y unos. Debajo de los segmentos hay una etiqueta más grande, punto.

    Así, cada periodo contiene una posición para los valores de uno, diez y cien. Observe que, al mirar de derecha a izquierda, el valor de cada posición es diez veces el anterior. Cada periodo tiene un nombre particular.

    Una serie de grupos de tres segmentos, separados por comas. Los segmentos están etiquetados, de izquierda a derecha, billones, miles de millones, miles y unidades.

    A medida que continuamos de derecha a izquierda, hay más periodos. Los cinco periodos enumerados anteriormente son los más comunes, y en nuestro estudio de las matemáticas introductorias, son suficientes.

    El siguiente diagrama ilustra nuestro sistema de números posicionales a billones. (Hay, para estar seguro, otros periodos.)

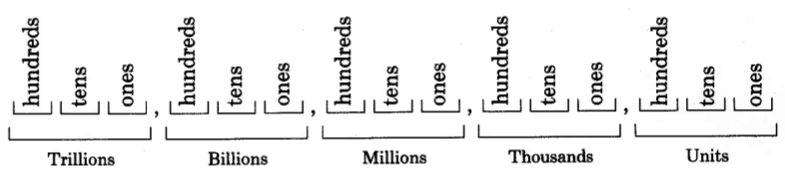
    Una serie de grupos de tres segmentos, separados por comas. Los grupos de segmentos están etiquetados, de izquierda a derecha, billones, miles de millones, miles y unidades. Cada segmento del grupo de tres tiene una etiqueta. De izquierda a derecha, en cada grupo, los segmentos se etiquetan cientos, decenas y unos.

    En nuestro sistema de números posicionales, el valor de un dígito está determinado por su posición en el número.

    Conjunto de Muestras B

    Encuentra el valor de 6 en el número 7,261.

    Solución

    Dado que 6 está en la posición de decenas del periodo de unidades, su valor es de 6 decenas.

    6 decenas\(=60\)

    Conjunto de Muestras B

    Encuentra el valor de 9 en el número 86,932,106,005.

    Solución

    Dado que 9 se encuentra en la posición de cientos del periodo de millones, su valor es de 9cientos millones.

    9 mil millones = 9 mil millones

    Conjunto de Muestras B

    Encuentra el valor de 2 en el número 102,001.

    Solución

    Ya que 2 está en la posición de unos del periodo de miles, su valor es de 2 mil.

    2 mil = 2 mil

    Set de práctica B

    Encuentra el valor de 5 en el número 65,000.

    Contestar

    cinco mil

    Set de práctica B

    Encuentra el valor de 4 en el número 439,997,007,010.

    Contestar

    cuatrocientos mil millones

    Set de práctica B

    Encuentra el valor de 0 en el número 108.

    Contestar

    cero decenas, o cero

    Números Enteros

    Definición: Números enteros

    Números que se forman usando solo los dígitos

    0 1 2 3 4 5 6 7 8 9

    se llaman números enteros. Ellos son

    0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,...

    Los tres puntos al final significan “y así sucesivamente en este mismo patrón”.

    Graficar números enteros

    Definición: Línea numérica

    Los números enteros pueden visualizarse construyendo una línea numérica. Para construir una recta numérica, simplemente dibujamos una línea recta y elegimos cualquier punto de la línea y la etiquetamos como 0.

    Definición: Origen

    A este punto se le llama el origen. Luego elegimos una longitud conveniente, y moviéndonos hacia la derecha, marcamos intervalos consecutivos (partes) a lo largo de la línea comenzando en 0. Etiquetamos cada nuevo punto final de intervalo con el siguiente número entero.

    Una línea con flechas a la izquierda y a la derecha. A lo largo de la línea hay guiones espaciados uniformemente, numerados del 0 al 10 de la izquierda a la derecha de la línea.

    Definición: Graficar

    Podemos mostrar visualmente un número entero dibujando un círculo cerrado en el punto etiquetado con ese número entero. Otra frase para mostrar visualmente un número entero es graficar el número entero. La palabra gráfica significa “mostrar visualmente”.

    Conjunto de Muestras C

    Grafica los siguientes números enteros: 3, 5, 9.

    Una línea numérica de 0 a 11. Hay puntos en la parte superior de los guiones etiquetados, 3, 5 y 9.

    Conjunto de Muestras C

    Especifique los números enteros que se grafican en la siguiente línea numérica. La ruptura en la recta numérica indica que estamos al tanto de los números enteros entre 0 y 106, y 107 y 872, pero no los estamos listando debido a limitaciones de espacio.

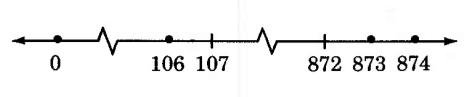
    Una línea numérica del 0 al 874, sin mostrar todos los números enteros entre 0 y 874. Hay dos roturas dentadas en la línea, una entre 0 y 106, y otra entre 107 y 872. Hay puntos en los guiones para 0, 106, 873 y 874.

    Solución

    Los números que se han graficado son

    0, 106, 873, 874

    Set de práctica C

    Grafica los siguientes números enteros: 46, 47, 48, 325, 327.

    Una línea con flechas a la izquierda y a la derecha. La línea tiene dos roturas dentadas.

    Contestar

    Una línea numérica de 0 a 327, con no todos los números enteros entre 0 y 327 mostrados. Hay dos roturas dentadas en la línea, una entre 0 y 46, y otra entre 48 y 325. Hay puntos en los guiones para 46, 47, 48, 325 y 327.

    Set de práctica C

    Especifique los números enteros que se grafican en la siguiente línea numérica.

    Una línea numérica entre 0 y 979, con no todos los números enteros entre 0 y 979 mostrados. Hay dos roturas dentadas en la línea, una entre 6 y 112, y otra entre 113 y 978. Hay puntos en los guiones para 4, 5, 6, 113 y 978.

    Contestar

    4, 5, 6, 113, 978

    Una línea está compuesta por un sinfín de puntos. Observe que hemos etiquetado solo algunos de ellos. A medida que avanzamos, descubriremos nuevos tipos de números y determinaremos su ubicación en la línea numérica.

    Ejercicios

    Ejercicio\(\PageIndex{1}\)

    ¿Qué es un número?

    Contestar

    concepto

    Ejercicio\(\PageIndex{2}\)

    ¿Qué es un numeral?

    ¿La palabra “once” califica como numeral?

    Contestar

    Sí, ya que es un símbolo que representa un número.

    Ejercicio\(\PageIndex{3}\)

    ¿Cuántos dígitos diferentes hay?

    Nuestro sistema numérico, el sistema numérico Hindu-Árabe, es un sistema numérico con base?

    Contestar

    posicional; 10

    Ejercicio\(\PageIndex{4}\)

    Los números compuestos por más de tres dígitos a veces se separan en grupos de tres por comas. A estos grupos de tres se les llama.

    En nuestro sistema numérico, cada periodo tiene tres valores asignados a él. Estos valores son los mismos para cada periodo. De derecha a izquierda, ¿qué son?

    Contestar

    unos, decenas, cientos

    Ejercicio\(\PageIndex{5}\)

    Cada periodo tiene su propio nombre particular. De derecha a izquierda, ¿cuáles son los nombres de los cuatro primeros?

    En el número 841, ¿cuántas decenas hay?

    Contestar

    4

    Ejercicio\(\PageIndex{6}\)

    En el número 3,392, ¿cuántos hay?

    En el número 10,046, ¿cuántos miles hay?

    Contestar

    0

    Ejercicio\(\PageIndex{7}\)

    En el número 779,844,205, ¿cuántos diez millones hay?

    En el número 65.021, ¿cuántos cientos de miles hay?

    Contestar

    0

    Para los siguientes problemas, dé el valor del dígito indicado en el número dado.

    Ejercicio\(\PageIndex{8}\)

    5 en 599

    1 en 310,406

    Contestar

    diez mil

    Ejercicio\(\PageIndex{9}\)

    9 en 29,827

    6 en 52,561,001,100

    Contestar

    6 diez millones = 60 millones

    Ejercicio\(\PageIndex{10}\)

    Escribe un número de dos dígitos que tenga un ocho en la posición de decenas.

    Escribe un número de cuatro dígitos que tenga un uno en la posición de miles y un cero en la posición de unos.

    Responder

    1,340 (las respuestas pueden variar)

    Ejercicio\(\PageIndex{11}\)

    ¿Cuántos números enteros de dos dígitos hay?

    ¿Cuántos números enteros de tres dígitos hay?

    Responder

    900

    Ejercicio\(\PageIndex{12}\)

    ¿Cuántos números enteros de cuatro dígitos hay?

    ¿Hay un número entero más pequeño? Si es así, ¿qué es?

    Responder

    sí; cero

    Ejercicio\(\PageIndex{13}\)

    ¿Hay un número entero más grande? Si es así, ¿qué es?

    Otro término para “mostrar visualmente” es?

    Responder

    graficar

    Ejercicio\(\PageIndex{14}\)

    Los números enteros se pueden mostrar visualmente en un.

    Grafique (visualice visualmente) los siguientes números enteros en la línea numérica a continuación: 0, 1, 31, 34.

    Una línea numérica del 0 al 34, sin mostrar todos los números entre 0 y 34. Hay una ruptura dentada en la línea entre 4 y 29.

    Responder

    Una línea numérica del 0 al 34, con no todos los números enteros entre 0 y 34 mostrados. Hay una ruptura dentada en la línea, entre 4 y 29. Hay puntos en los guiones para 1, 31 y 34.

    Ejercicio\(\PageIndex{15}\)

    Construir una recta numérica en el espacio proporcionado a continuación y graficar (mostrar visualmente) los siguientes números enteros: 84, 85, 901, 1006, 1007.

    Especifique, en su caso, los números enteros que se grafican en la siguiente línea numérica.

    Una línea numérica de 0 a 102, con no todos los números enteros entre 0 y 102 mostrados. Hay dos roturas dentadas en la línea, una entre 0 y 61, y otra entre 64 y 99. Hay puntos en los guiones para 61, 99, 100 y 102.

    Responder

    61, 99, 100, 102

    Ejercicio\(\PageIndex{16}\)

    Especifique, en su caso, los números enteros que se grafican en la siguiente línea numérica.

    Una línea numérica del 0 al 87, con no todos los números enteros entre 0 y 87 mostrados. Hay tres roturas dentadas en la línea, una entre 1 y 8, una entre 11 y 73, y una entre 74 y 85.

    This page titled 1.1: Números enteros is shared under a CC BY license and was authored, remixed, and/or curated by Denny Burzynski & Wade Ellis, Jr. (OpenStax CNX) .