1.6: Propiedades de Adición

Última actualización
Guardar como PDF

Page ID: 116294

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

comprender las propiedades conmutativas y asociativas de la adición
entender por qué 0 es la identidad aditiva

Consideramos ahora tres propiedades simples pero muy importantes de adición.

La propiedad conmutativa de la adición

Definición: Propiedad conmutativa de adición

Si se agregan dos números enteros en cualquier orden, la suma no cambiará.

Conjunto de Muestras A

Sumar los números enteros

$8 y 5.$

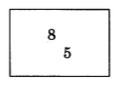
8 + 5 = 13
5 + 8 = 13

Los números 8 y 5 se pueden sumar en cualquier orden. Independientemente del orden en que se sumen, la suma es de 13.

Conjunto de práctica A

Utilice la propiedad conmutativa de suma para encontrar la suma de 12 y 41 de dos maneras diferentes.

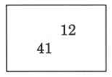
$41 y 12.$

Contestar: 12 + 41 = 53 y 41 + 12 = 53

Conjunto de práctica A

Sumar los números enteros

$1,958 y 837.$

Contestar: 837 + 1,958 = 2,795 y 1,958 + 837 = 2,795

Propiedad asociativa de adición

Si se van a sumar tres números enteros, la suma será la misma si primero se agregan los dos primeros, luego esa suma se agrega al tercero, o bien, los dos segundos se agregan primero, y esa suma se agrega al primero.

Uso de paréntesis

Es una práctica matemática común usar paréntesis para mostrar qué par de números queremos combinar primero.

Conjunto de Muestras B

Sumar los números enteros.

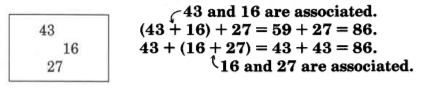
$43, 16 y 27. Se muestran dos ecuaciones. (43 + 16) + 27 = 59 + 27 = 86. 43 + (16 + 27) = 43 +43 = 86. Las flechas apuntan a las dos agrupaciones de números entre paréntesis para mostrar que están asociados.$

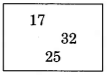
Set de práctica B

Utilice la propiedad asociativa de suma para agregar los siguientes números enteros de dos maneras diferentes.

$17, 32 y 25.$

Contestar: (17 + 32) + 25 = 49 + 25 = 74 y 17 + (32 + 25) = 17 + 57 = 74

Set de práctica B

$1,629, 806 y 429.$

Contestar

(1,629 + 806) + 429 = 2,435 + 429 = 2,864

1,629 + (806 + 429) = 1,629 + 1,235 = 2,864

La identidad aditiva

0 Es la identidad aditiva

El número entero 0 se llama la identidad aditiva, ya que cuando se agrega a cualquier número entero, la suma es idéntica a ese número entero.

Conjunto de Muestras C

Sumar los números enteros.

$29 y 0.$

29 + 0 = 29
0 + 29 = 29

Cero agregado a 29 no cambia la identidad de 29.

Set de práctica C

Suma los siguientes números enteros.

$0 y 8.$

Contestar: 8

Set de práctica C

$0 y 5.$

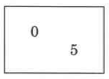
Contestar: 5

Supongamos que dejamos que la letra x represente una elección para algún número entero. Para los dos primeros problemas, encuentra las sumas. Para el tercer problema, encuentra la suma siempre que ahora sabemos que x representa el número entero 17.

Set de práctica C

$x y 0.$

Contestar: x

Set de práctica C

$x y 0.$

Contestar: x

Set de práctica C

$0 y x.$

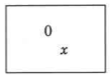
Contestar: 17

Ejercicios

Para los siguientes problemas, agregue los números de dos maneras.

Ejercicio$\PageIndex{1}$

$8 y 29.$

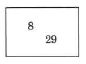
Contestar: 37

Ejercicio$\PageIndex{2}$

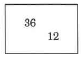
$36 y 12.$

Ejercicio$\PageIndex{3}$

$48 y 36.$

Contestar: 45

Ejercicio$\PageIndex{4}$

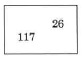
$117 y 26.$

Ejercicio$\PageIndex{5}$

$456 y 112.$

Contestar: 568

Ejercicio$\PageIndex{6}$

$4,251 y 1,096.$

Ejercicio$\PageIndex{7}$

$73,205 y 49,118.$

Contestar: 122,323

Ejercicio$\PageIndex{8}$

$265,094 y 32,508.$

Ejercicio$\PageIndex{9}$

$5, 32 y 8.$

Contestar: 45

Ejercicio$\PageIndex{10}$

$18, 16 y 14.$

Ejercicio$\PageIndex{11}$

$10, 52 y 38.$

Contestar: 100

Ejercicio$\PageIndex{12}$

$36, 84 y 7.$

Ejercicio$\PageIndex{13}$

$17, 114, y 425.$

Contestar: 556

Ejercicio$\PageIndex{14}$

$11, 1019 y 586.$

Ejercicio$\PageIndex{15}$

$37 mil 728, 4 mil 472 y 1 mil 261.$

Contestar: 43,461

Para los siguientes problemas, mostrar que los pares de cantidades rinden la misma suma.

Ejercicio$\PageIndex{16}$

(11 + 27) + 9 y 11 + (27 + 9)

Ejercicio$\PageIndex{17}$

(80 + 52) + 6 y 80 + (52 + 6)

Contestar: 132 + 6 = 80 + 58 = 138

Ejercicio$\PageIndex{18}$

(114 + 226) + 108 y 114 + (226 + 108)

Ejercicio$\PageIndex{19}$

(731 + 256) + 171 y 731 + (256 + 171)

Contestar: 987 + 171 = 731 + 427 = 1,158

Ejercicio$\PageIndex{20}$

El hecho de que (un primer número + un segundo número) + tercer número = un primer número + (un segundo número + un tercer número) es un ejemplo de la propiedad de suma.

Ejercicio$\PageIndex{21}$

El hecho de que 0 + cualquier número = ese número en particular es un ejemplo de la propiedad de suma.

Contestar: Identidad

Ejercicio$\PageIndex{22}$

El hecho de que un primer número + un segundo número = un segundo número + un primer número es un ejemplo de la propiedad de suma.

Ejercicio$\PageIndex{23}$

Utilice los números 15 y 8 para ilustrar la propiedad conmutativa de la suma.

Contestar: 15 + 8 = 8 + 15 = 23

Ejercicio$\PageIndex{22}$

Utilice los números 6, 5 y 11 para ilustrar la propiedad asociativa de la suma.

Ejercicio$\PageIndex{23}$

El número cero se llama identidad aditiva. ¿Por qué es tan apropiado el término identidad?

Contestar: ... porque su socio además sigue siendo idénticamente el mismo después de esa adición

Ejercicios para la revisión

Ejercicio$\PageIndex{24}$

¿Cuántos cientos en 46,581?

Ejercicio$\PageIndex{25}$

Escribe 2,218 como lo leerías.

Contestar: Dos mil doscientos dieciocho.

Ejercicio$\PageIndex{26}$

Vuelta 506,207 al mil más cercano.

Ejercicio$\PageIndex{27}$

Encuentra la suma de$\begin{array} {r} {482} \\ {\underline{+\ \ 68}} \end{array}$

Contestar: 550

Ejercicio$\PageIndex{28}$

Encuentra la diferencia:$\begin{array} {r} {3,318} \\ {\underline{-\ \ 429}} \end{array}$