4.7: Resumen de conceptos clave

Última actualización
Guardar como PDF

Page ID: 116706

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Resumen de Key Concepts

Fracción
La idea de dividir una cantidad entera en partes iguales nos da la palabra fracción.

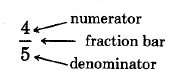
Fracción Bar, Denominador, Numerador
Una fracción tiene tres partes:

La barra de fracción -
El número entero distinto de cero por debajo de la barra de fracciones es el denominador.
El número entero por encima de la barra de fracciones es el numerador.

$Cuatro quintos. Cuatro es el numerador, cinco es el denominador, y una línea entre ellos es la barra de fracción.$

Fracción
propia Las fracciones propias son fracciones en las que el numerador es estrictamente menor que el denominador.
$\dfrac{4}{5}$es una fracción propiamente dicha

Fracción
impropia Las fracciones impropias son fracciones en las que el numerador es mayor o igual que el denominador. Además, cualquier número distinto de cero colocado sobre 1 es una fracción impropia.
$\dfrac{5}{4}$,$\dfrac{5}{5}$, y$\dfrac{5}{1}$ son fracciones impropias.

Número mixto
Un número mixto es un número que es la suma de un número entero y una fracción propia.
$1\dfrac{1}{5}$es un número mixto$(1 \dfrac{1}{5} = 1 + \dfrac{1}{5})$

Correspondencia Entre Fracciones Impropias y Números Mixtos
Cada fracción impropia corresponde a un número mixto particular, y cada número mixto corresponde a una fracción impropia particular.

Convertir una Fracción Impropia a
un Método de Número Mixto A, basado en la división, convierte una fracción impropia en un número mixto equivalente.
$\dfrac{5}{4}$se puede convertir a$1\dfrac{1}{4}$

Convertir un Número Mixto en una Fracción Impropia El método
A, basado en la multiplicación, convierte un número mixto en una fracción impropia equivalente.
$5\dfrac{7}{8}$se puede convertir a$\dfrac{47}{8}$

Fracciones equivalentes
Las fracciones que representan la misma cantidad son fracciones equivalentes.
$\dfrac{3}{4}$y$\dfrac{6}{8}$ son fracciones equivalentes

Prueba para Fracciones Equivalentes
Si los productos cruzados de dos fracciones son iguales, entonces las dos fracciones son equivalentes.

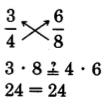
$Tres cuartos y seis octavos, con una flecha de cada denominador apuntando hacia arriba al numerador de la fracción opuesta. Esto hace que tres por ocho sea igual a cuatro por seis, lo que equivale a veinticuatro en ambos lados.$

Así,$\dfrac{3}{4}$ y$\dfrac{6}{8}$ son equivalentes.

Relativamente Prime
Dos números enteros son relativamente primos cuando 1 es el único número que divide a ambos.
3 y 4 son relativamente primos

Reducido a términos más bajos
Una fracción se reduce a términos más bajos si su numerador y denominador son relativamente primos.
El número$\dfrac{3}{4}$ se reduce a términos más bajos, ya que 3 y 4 son relativamente primos.
El número no$\dfrac{6}{8}$ se reduce a términos más bajos ya que 6 y 8 no son relativamente primos.

Reducir fracciones a términos más bajos
Dos métodos, uno basado en dividir primos comunes y otro basado en dividir cualquier factor común, están disponibles para reducir una fracción a términos más bajos.

Elevar fracciones a términos más altos
Una fracción puede elevarse a términos más altos multiplicando tanto el numerador como el denominador por el mismo número distinto de cero.
$\dfrac{3}{4} = \dfrac{3 \cdot 2}{4 \cdot 2} = \dfrac{6}{8}$

La Palabra “DE” Significa Multiplicación
En muchas aplicaciones matemáticas, la palabra “de” significa multiplicación.

Multiplicación de Fracciones
Para multiplicar dos o más fracciones, multiplicar los numeradores juntos y multiplicar los denominadores juntos. Reducir si es posible.
$\dfrac{5}{8} \cdot \dfrac{4}{15} = \dfrac{5 \cdot 4}{8 \cdot 15} = \dfrac{20}{120} = \dfrac{1}{6}$

Multiplicar fracciones dividiendo factores comunes
Dos o más fracciones se pueden multiplicar dividiendo primero los factores comunes y luego usando la regla para multiplicar fracciones.

$\dfrac{\begin{array} {c} {^1} \\ {\cancel{5}} \end{array}}{\begin{array} {c} {\cancel{8}} \\ {^2} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{4}} \end{array}}{\begin{array} {c} {\cancel{15}} \\ {^3} \end{array}} = \dfrac{1 \cdot 1}{2 \cdot 3} = \dfrac{1}{6}$

Multiplicación de números mixtos
Para realizar una multiplicación en la que haya números mixtos, primero convierta cada número mixto a una fracción impropia, luego multiplique. Esta idea también se aplica a la división de números mixtos.

Reciprocales
Dos números cuyo producto es 1 son recíprocos.
7 y$\dfrac{1}{7}$ son recíprocos

División de Fracciones
Para dividir una fracción por otra fracción, multiplique el dividendo por el recíproco del divisor.
$\dfrac{1}{\dfrac{3}{7}} = \dfrac{7}{3}$

Declaraciones de multiplicación
Una declaración matemática de la forma

producto = (factor 1) (factor 2)

es una declaración de multiplicación.

Al omitir uno de los tres números, resulta uno de los tres siguientes problemas:

M = (factor 1)$\cdot$ (factor 2) Falta la declaración del producto.
product = (factor 1)$\cdot$ M Falta la declaración del factor.
product = M$\cdot$ (factor 2) Falta la declaración del factor.

Los productos faltantes se determinan simplemente multiplicando los factores conocidos. Los factores faltantes están determinados por

factor faltante = (producto)$\div$ (factor conocido)