4.6: Aplicaciones que involucran fracciones

Última actualización
Guardar como PDF

Page ID: 116692

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

ser capaz de resolver declaraciones de productos faltantes
ser capaz de resolver declaraciones de factores faltantes

Declaraciones de multiplicación

Declaración, Declaración de multiplicación
Una declaración es una oración que es verdadera o falsa. Una declaración matemática de la forma

product = (factor 1) ⋅ (factor 2)

es una declaración de multiplicación. Dependiendo de los números que se utilicen, puede ser verdadero o falso.

Omitir exactamente uno de los tres números del enunciado producirá exactamente uno de los tres problemas siguientes. Para mayor comodidad, representaremos el número omitido (o faltante) con la letra M (M para Falta).

M = (factor 1) ⋅ (factor 2) Falta la declaración del producto.
M ⋅ (factor 2) = producto Falta la declaración del factor.
(factor 1) ⋅ M = producto Falta la declaración del factor.

Nos interesa desarrollar y trabajar con métodos para determinar el número faltante que haga verdadera la afirmación. Fundamental para estos métodos es la capacidad de traducir dos palabras a símbolos matemáticos. La palabra

de traduce a tiempos
se traduce a iguales

Declaraciones de productos faltantes

La ecuación$M = 8 \cdot 4$ es una declaración de producto faltante. Podemos encontrar el valor de M que hace cierta esta afirmación multiplicando los factores conocidos.

Las declaraciones de producto faltantes se pueden utilizar para determinar la respuesta a una pregunta como, “¿Qué número es la fracción 1 de la fracción 2?

Conjunto de Muestras A

Hallar$\dfrac{3}{4}$ de$\dfrac{8}{9}$. Nos están haciendo la pregunta: “¿Qué número es$\dfrac{3}{4}$ de$\dfrac{8}{9}$?” Debemos traducir de palabras a símbolos matemáticos.

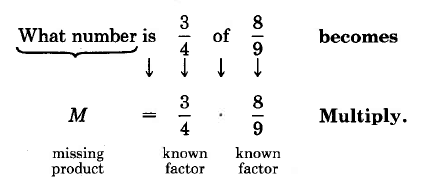
$Dos declaraciones seguidas. Cada elemento está alineado con algo por encima de él. Primero, qué número es tres cuartas partes de ocho novenésimas, se convierte. Segundo, M equivale a tres cuartos por ocho novenos, multiplicar. M es el producto faltante, y tres cuartos y ocho novenos son factores conocidos.$

$M = \dfrac{\begin{array} {c} {^1} \\ {\cancel{3}} \end{array}}{\begin{array} {c} {\cancel{4}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^2} \\ {\cancel{8}} \end{array}}{\begin{array} {c} {\cancel{9}} \\ {^3} \end{array}} = \dfrac{1 \cdot 2}{1 \cdot 3} = \dfrac{2}{3}$

Así,$\dfrac{3}{4}$ de$\dfrac{8}{9}$ es$\dfrac{2}{3}$.

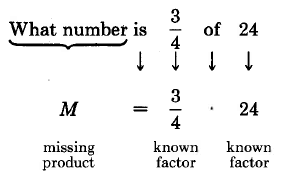
$Dos declaraciones seguidas. Cada elemento está alineado con algo por encima de él. Primero, qué número son las tres cuartas partes de veinticuatro. Segundo, M equivale a tres cuartos por veinticuatro. M es el producto faltante, y tres cuartos y ocho novenos son factores conocidos.$

$M = \dfrac{3}{\begin{array} {c} {\cancel{4}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^6} \\ {\cancel{24}} \end{array}}{1} = \dfrac{3 \cdot 6}{1 \cdot 1} = \dfrac{18}{1} = 18$

Así, 18 es$\dfrac{3}{4}$ de 24.

Conjunto de práctica A

Hallar$\dfrac{3}{8}$ de$\dfrac{16}{15}$.

Contestar: $\dfrac{2}{5}$

Conjunto de práctica A

¿De qué$\dfrac{9}{10}$ número es$\dfrac{5}{6}$?

Contestar: $\dfrac{3}{4}$

Conjunto de práctica A

$\dfrac{11}{16}$de$\dfrac{8}{33}$ es ¿qué número?

Contestar: $\dfrac{1}{6}$

Declaraciones de factores faltantes

La ecuación$8 \cdot M = 32$ es una declaración de factor faltante. Podemos encontrar el valor de$M$ que hace que esta afirmación sea cierta dividiendo (ya que sabemos eso$32 \div 8 = 4$.

$La expresión 8 veces M es igual a 32 significa que M es igual a treinta y dos dividido por ocho. M es el factor faltante, treinta y dos es el producto y ocho es el factor conocido.$

Encontrar el factor faltante
Para encontrar el factor faltante en una declaración de factor faltante, divida el producto por el factor conocido.
factor faltante = (producto)$\div$ (factor conocido)

Las declaraciones de factores faltantes se pueden usar para responder preguntas como

$\dfrac{3}{8}$¿de qué número es$\dfrac{9}{4}$?
¿Qué parte de$1 \dfrac{2}{7}$ es$1 \dfrac{13}{14}$?

Conjunto de Muestras B

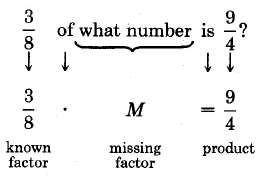
$¿Tres octavos de qué número son nueve cuartas partes? Esto es lo mismo que tres octavos por M equivale a nueve cuartas partes. Tres octavos es el factor conocido, M es el factor faltante y nueve cuartos es el producto.$

Ahora, usando

factor faltante = (producto)$\div$ (factor conocido)

Obtenemos

$\begin{array} {rcl} {M = \dfrac{9}{4} \div \dfrac{3}{8} = \dfrac{9}{4} \cdot \dfrac{8}{3}} & = & {\dfrac{\begin{array} {c} {^3} \\ {\cancel{9}} \end{array}}{\begin{array} {c} {\cancel{4}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^2} \\ {\cancel{8}} \end{array}}{\begin{array} {c} {\cancel{3}} \\ {^1} \end{array}}} \\ {} & = & {\dfrac{3 \cdot 2}{1 \cdot 1}} \\ {} & = & {6} \end{array}$

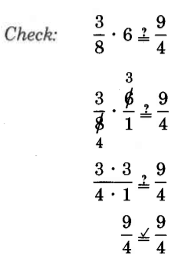
$Revisa la obra: ¿tres octavos por seis es igual a nueve cuartas partes? Cancele el seis y el ocho dividiendo cada uno por dos. Esto se puede simplificar para averiguar que sí, son iguales.$

Así,$\dfrac{3}{8}$ de 6 es$\dfrac{9}{4}$.

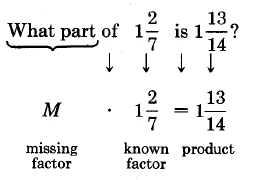
$¿Qué parte de 1 y dos séptimos es 1 y trece cuartas partes? Esto equivale a M por 1 y dos séptimos equivale a 1 y trece cuartas partes. M es el factor faltante, 1 y dos séptimos es el factor conocido, y 1 y trece cuartas partes es el producto.$

Para mayor comodidad, convertiremos los números mixtos en fracciones impropias.

$M \cdot \dfrac{9}{7} = \dfrac{27}{14}$

Ahora, usando

factor faltante = (producto)$\div$ (factor conocido)

obtenemos

$\begin{array} {rcl} {M = \dfrac{27}{14} \div \dfrac{9}{7} = \dfrac{27}{14} \cdot \dfrac{7}{9}} & = & {\dfrac{\begin{array} {c} {^3} \\ {\cancel{27}} \end{array}}{\begin{array} {c} {\cancel{14}} \\ {^2} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{7}} \end{array}}{\begin{array} {c} {\cancel{9}} \\ {^1} \end{array}}} \\ {} & = & {\dfrac{3 \cdot 1}{2 \cdot 1}} \\ {} & = & {\dfrac{3}{2}} \end{array}$

$Cheque: ¿tres mitades por nueve séptimos es igual a veintisiete catorce? Sí.$

Así,$\dfrac{3}{2}$ de$1 \dfrac{2}{7}$ es$1 \dfrac{13}{14}$.

Set de práctica B

$\dfrac{3}{5}$¿de qué número es$\dfrac{9}{20}$?

Contestar: $\dfrac{3}{4}$

Set de práctica B

$3 \dfrac{3}{4}$¿de qué número es$2 \dfrac{2}{9}$?

Contestar: $\dfrac{16}{27}$

Set de práctica B

¿Qué parte de$\dfrac{3}{5}$ es$\dfrac{9}{10}$?

Contestar: $1 \dfrac{1}{2}$

Set de práctica B

¿Qué parte de$1 \dfrac{1}{4}$ es$1 \dfrac{7}{8}$?

Contestar: $1 \dfrac{1}{2}$

Ejercicios

Ejercicio$\PageIndex{1}$

Hallar$\dfrac{2}{3}$ de$\dfrac{3}{4}$.

Contestar: $\dfrac{1}{2}$

Ejercicio$\PageIndex{2}$

Hallar$\dfrac{5}{8}$ de$\dfrac{1}{10}$.

Ejercicio$\PageIndex{3}$

Hallar$\dfrac{12}{13}$ de$\dfrac{13}{36}$.

Contestar: $\dfrac{1}{3}$

Ejercicio$\PageIndex{4}$

Hallar$\dfrac{1}{4}$ de$\dfrac{4}{7}$.

Ejercicio$\PageIndex{5}$

$\dfrac{3}{10}$de$\dfrac{15}{4}$ es ¿qué número?

Contestar: $\dfrac{9}{8}$o$1 \dfrac{1}{8}$

Ejercicio$\PageIndex{6}$

$\dfrac{14}{15}$de$\dfrac{20}{21}$ es ¿qué número?

Ejercicio$\PageIndex{7}$

$\dfrac{3}{44}$de$\dfrac{11}{12}$ es ¿qué número?

Contestar: $\dfrac{1}{16}$

Ejercicio$\PageIndex{8}$

$\dfrac{1}{3}$de 2 es ¿qué número?

Ejercicio$\PageIndex{9}$

$\dfrac{1}{4}$de 3 es ¿qué número?

Contestar: $\dfrac{3}{4}$

Ejercicio$\PageIndex{10}$

$\dfrac{1}{10}$de$\dfrac{1}{100}$ es ¿qué número?

Ejercicio$\PageIndex{11}$

$\dfrac{1}{100}$de$\dfrac{1}{10}$ es ¿qué número?

Contestar: $\dfrac{1}{1,000}$

Ejercicio$\PageIndex{12}$

$1 \dfrac{5}{9}$de$2 \dfrac{4}{7}$ es ¿qué número?

Ejercicio$\PageIndex{13}$

$1 \dfrac{7}{18}$de$\dfrac{4}{15}$ es ¿qué número?

Contestar: $\dfrac{10}{27}$

Ejercicio$\PageIndex{14}$

$1 \dfrac{1}{8}$de$1 \dfrac{11}{16}$ es ¿qué número?

Ejercicio$\PageIndex{15}$

Hallar$\dfrac{2}{3}$$\dfrac{1}{6}$ de$\dfrac{9}{2}$.

Contestar: $\dfrac{1}{2}$

Ejercicio$\PageIndex{16}$

Hallar$\dfrac{5}{8}$$\dfrac{9}{20}$ de$\dfrac{4}{9}$.

Ejercicio$\PageIndex{17}$

$\dfrac{5}{12}$de que numero es$\dfrac{5}{6}$?

Contestar: 2

Ejercicio$\PageIndex{18}$

$\dfrac{3}{14}$de que numero es$\dfrac{6}{7}$?

Ejercicio$\PageIndex{19}$

$\dfrac{10}{3}$de que numero es$\dfrac{5}{9}$?

Contestar: $\dfrac{1}{6}$

Ejercicio$\PageIndex{20}$

$\dfrac{15}{7}$de que numero es$\dfrac{20}{21}$?

Ejercicio$\PageIndex{21}$

$\dfrac{8}{3}$de que numero es$1 \dfrac{7}{9}$?

Contestar: $\dfrac{2}{3}$

Ejercicio$\PageIndex{22}$

$\dfrac{1}{3}$de que numero es$\dfrac{1}{3}$?

Ejercicio$\PageIndex{23}$

$\dfrac{1}{6}$de que numero es$\dfrac{1}{6}$?

Contestar: 1

Ejercicio$\PageIndex{24}$

$\dfrac{3}{4}$de que numero es$\dfrac{3}{4}$?

Ejercicio$\PageIndex{25}$

$\dfrac{8}{11}$de que numero es$\dfrac{8}{11}$?

Contestar: 1

Ejercicio$\PageIndex{26}$

$\dfrac{3}{8}$de que numero es 0?

Ejercicio$\PageIndex{27}$

$\dfrac{2}{3}$de que numero es 1?

Contestar: $\dfrac{3}{2}$o$1 \dfrac{1}{2}$

Ejercicio$\PageIndex{28}$

$3 \dfrac{1}{5}$de que numero es 1?

Ejercicio$\PageIndex{29}$

$1 \dfrac{9}{12}$de que numero es$5 \dfrac{1}{4}$?

Contestar: 3

Ejercicio$\PageIndex{30}$

$3 \dfrac{1}{25}$de que numero es$2 \dfrac{8}{15}$?

Ejercicio$\PageIndex{31}$

¿Qué parte de$\dfrac{2}{3}$ es$1 \dfrac{1}{9}$?

Contestar: $\dfrac{5}{3}$o$1 \dfrac{2}{3}$

Ejercicio$\PageIndex{32}$

¿Qué parte de$\dfrac{9}{10}$ es$3 \dfrac{3}{5}$?

Ejercicio$\PageIndex{33}$

¿Qué parte de$\dfrac{8}{9}$ es$\dfrac{3}{5}$?

Contestar: $\dfrac{27}{40}$

Ejercicio$\PageIndex{34}$

¿Qué parte de$\dfrac{14}{15}$ es$\dfrac{7}{30}$?

Ejercicio$\PageIndex{35}$

¿Qué parte de 3 es$\dfrac{1}{5}$?

Contestar: $\dfrac{1}{15}$

Ejercicio$\PageIndex{36}$

¿Qué parte de 8 es$\dfrac{2}{3}$?

Ejercicio$\PageIndex{37}$

¿Qué parte de 24 es 9?

Contestar: $\dfrac{3}{8}$

Ejercicio$\PageIndex{38}$

¿Qué parte de 42 es 26?

Ejercicio$\PageIndex{39}$

Hallar$\dfrac{12}{13}$ de$\dfrac{39}{40}$.

Contestar: $\dfrac{9}{10}$

Ejercicio$\PageIndex{40}$

$\dfrac{14}{15}$de$\dfrac{12}{21}$ es ¿qué número?

Ejercicio$\PageIndex{41}$

$\dfrac{8}{15}$de que numero es$2 \dfrac{2}{5}$?

Contestar: $\dfrac{9}{2} = 4 \dfrac{1}{2}$

Ejercicio$\PageIndex{42}$

$\dfrac{11}{15}$de que numero es$\dfrac{22}{35}$?

Ejercicio$\PageIndex{43}$

$\dfrac{11}{16}$de que numero es 1?

Contestar: $\dfrac{16}{11}$o$1 \dfrac{5}{11}$

Ejercicio$\PageIndex{44}$

¿Qué parte de$\dfrac{23}{40}$ es$3 \dfrac{9}{20}$?

Ejercicio$\PageIndex{45}$

$\dfrac{4}{35}$de$3 \dfrac{9}{22}$ es ¿qué número?

Contestar: $\dfrac{30}{77}$

Ejercicios para la revisión

Ejercicio$\PageIndex{46}$

Utilice los números 2 y 7 para ilustrar la propiedad conmutativa de la suma.

Ejercicio$\PageIndex{47}$

¿Es 4 divisible por 0?

Contestar: no

Ejercicio$\PageIndex{48}$

Ampliar$3^7$. No encuentre el valor real.

Ejercicio$\PageIndex{49}$

Convertir$3 \dfrac{5}{12}$ a una fracción impropia.

Contestar: $\dfrac{41}{12}$

Ejercicio$\PageIndex{50}$

Encuentra el valor de$\dfrac{3}{8}$\ div\ dfrac {9} {16}\ cdot\ dfrac {6} {5}\).