5.1: Suma y resta de fracciones con denominadores similares

Última actualización
Guardar como PDF

Page ID: 116684

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

ser capaz de sumar y restar fracciones con denominadores similares

Adición de Fracción con denominadores similares

Examinemos el siguiente diagrama.

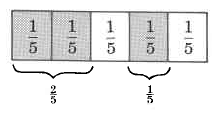
$Un rectángulo dividido en cinco partes. Cada parte está etiquetada como una quinta parte. Dos de las partes están sombreadas y etiquetadas con dos quintas partes. Una tercera parte está sombreada y está etiquetada como una quinta parte.$

2 una quintas partes y 1 una quinta parte está sombreada.

Se muestra en las regiones sombreadas del diagrama que

(2 quintas partes) + (1 una quinta parte) = (3 quintas partes)

Es decir,

$\dfrac{2}{5} + \dfrac{1}{5} = \dfrac{3}{5}$

A partir de esta observación, podemos sugerir la siguiente regla.

Método de sumar fracciones que tienen denominadores similares
Para sumar dos o más fracciones que tengan los mismos denominadores, agregue los numeradores y coloque la suma resultante sobre el denominador común. Reducir, si es necesario.

Conjunto de Muestras A

Encuentra las siguientes sumas.

$\dfrac{3}{7} + \dfrac{2}{7}$. Los denominadores son los mismos. Agrega los numeradores y coloca esa suma sobre 7.

Solución

$\dfrac{3}{7} + \dfrac{2}{7} = \dfrac{3 + 2}{7} = \dfrac{5}{7}$

Conjunto de Muestras A

$\dfrac{1}{8} + \dfrac{3}{8}$. Los denominadores son los mismos. Agrega los numeradores y coloca la suma sobre 8. Reducir.

Solución

$\dfrac{1}{8} + \dfrac{3}{8} = \dfrac{1 + 3}{8} = \dfrac{4}{8} = \dfrac{1}{2}$

Conjunto de Muestras A

$\dfrac{4}{9} + \dfrac{5}{9}$. Los denominadores son los mismos. Agrega los numeradores y coloca la suma sobre 9.

Solución

$\dfrac{4}{9} + \dfrac{5}{9} = \dfrac{4 + 5}{9} = \dfrac{9}{9} = 1$

Conjunto de Muestras A

$\dfrac{7}{8} + \dfrac{5}{8}$. Los denominadores son los mismos. Agrega los numeradores y coloca la suma sobre 8.

Solución

$\dfrac{7}{8} + \dfrac{5}{8} = \dfrac{7 + 5}{8} = \dfrac{12}{8} = \dfrac{3}{2}$

Conjunto de Muestras A

Para ver qué pasa si agregamos erróneamente los denominadores así como los numeradores, agreguemos

$\dfrac{1}{2} + \dfrac{1}{2}$

Agregar los numeradores y agregar erróneamente los denominadores produce

$\dfrac{1}{2} + \dfrac{1}{2} = \dfrac{1 + 1}{2 + 2} = \dfrac{2}{4} = \dfrac{1}{2}$

Esto quiere decir que dos$\dfrac{1}{2}$ es lo mismo que uno$\dfrac{1}{2}$. ¡Despregonada! No agregamos denominadores.

Conjunto de práctica A

Encuentra las siguientes sumas.

$\dfrac{1}{10} + \dfrac{3}{10}$

Contestar: $\dfrac{2}{5}$

Conjunto de práctica A

$\dfrac{1}{4} + \dfrac{1}{4}$

Contestar: $\dfrac{1}{2}$

Conjunto de práctica A

$\dfrac{7}{11} + \dfrac{4}{11}$

Contestar: $1$

Conjunto de práctica A

$\dfrac{3}{5} + \dfrac{1}{5}$

Contestar: $\dfrac{4}{5}$

Conjunto de práctica A

Mostrar por qué sumar tanto los numeradores como los denominadores es despreciable al sumar$\dfrac{3}{4}$$\dfrac{3}{4}$ y examinar el resultado.

Contestar: $\dfrac{3}{4} + \dfrac{3}{4} = \dfrac{3 + 3}{4 + 4} = \dfrac{6}{8} = \dfrac{3}{4}$, entonces dos$\dfrac{3}{4}$ = uno$\dfrac{3}{4}$, whihch es despreciable.

Resta de fracciones con denominadores similares

Podemos imaginarnos el concepto de resta de fracciones de la misma manera que imaginamos la suma.

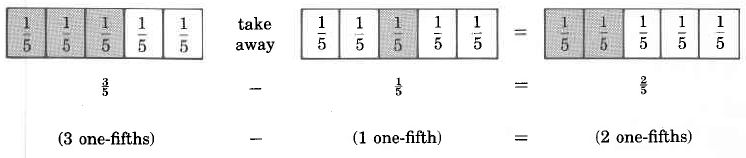
$Una visualización de un problema de sustracción. Se muestran tres filas, y cada fila tiene un elemento que se corresponde con ella. En la primera fila hay tres rectángulos, cada uno dividido en cinco partes. Cada parte de cada fracción está etiquetada como una quinta parte. El primer rectángulo tiene tres partes sombreadas. Al lado de esto está la declaración, para llevar. Al lado de esto está el segundo rectángulo, con una parte sombreada. Al lado de esto hay un signo de igual. Finalmente, el tercer rectángulo tiene dos partes sombreadas. La segunda fila dice tres quintos menos un quinto equivale a dos quintos. La tercera fila muestra la misma ecuación escrita en palabras.$

A partir de esta observación, podemos sugerir la siguiente regla para restar fracciones que tengan denominadores similares:

Resta de fracciones con denominadores similares
Para restar dos fracciones que tengan denominadores similares, restar los numeradores y colocar la diferencia resultante sobre el denominador común. Reducir, si es posible.

Conjunto de Muestras B

Encuentra las siguientes diferencias.

$\dfrac{3}{5} - \dfrac{1}{5}$. Los denominadores son los mismos. Restar los numeradores. Colocar la diferencia sobre 5.

Solución

$\dfrac{3}{5} - \dfrac{1}{5} = \dfrac{3 - 1}{5} = \dfrac{2}{5}$

Conjunto de Muestras B

$\dfrac{8}{6} - \dfrac{2}{6}$. Los denominadores son los mismos. Restar los numeradores. Coloca la diferencia sobre 6.

Solución

$\dfrac{8}{6} - \dfrac{2}{6} = \dfrac{8 - 2}{6} = \dfrac{6}{6} = 1$

Conjunto de Muestras B

$\dfrac{16}{9} - \dfrac{2}{9}$. Los denominadores son los mismos. Restar numeradores y colocar la diferencia sobre 9.

Solución

$\dfrac{16}{9} - \dfrac{2}{9} = \dfrac{16 - 2}{9} = \dfrac{14}{9}$

Conjunto de Muestras B

Para ver qué pasa si restamos erróneamente los denominadores, consideremos

$\dfrac{7}{15} - \dfrac{4}{15} = \dfrac{7 - 4}{15 - 15} = \dfrac{3}{0}$

Obtenemos división por cero, que no está definida. No restamos denominadores.

Set de práctica B

Encuentra las siguientes diferencias.

$\dfrac{10}{13} - \dfrac{8}{13}$

Contestar: $\dfrac{2}{13}$

Set de práctica B

$\dfrac{5}{12} - \dfrac{1}{12}$

Contestar: $\dfrac{1}{3}$

Set de práctica B

$\dfrac{1}{2} - \dfrac{1}{2}$

Contestar: 0

Set de práctica B

$\dfrac{26}{10} - \dfrac{14}{10}$

Contestar: $\dfrac{6}{5}$

Set de práctica B

Mostrar por qué restar tanto los numeradores como los denominadores es un error al realizar la resta$\dfrac{5}{9} - \dfrac{2}{9}$

Contestar: $\dfrac{5}{9} - \dfrac{2}{9} = \dfrac{5 - 2}{9 - 9} = \dfrac{3}{0}$, que no está definido

Ejercicios

Para los siguientes problemas, encuentra las sumas y diferencias. Asegúrese de reducir.

Ejercicio$\PageIndex{1}$

$\dfrac{3}{8} + \dfrac{2}{8}$

Contestar: $\dfrac{5}{8}$

Ejercicio$\PageIndex{2}$

$\dfrac{1}{6} + \dfrac{2}{6}$

Ejercicio$\PageIndex{3}$

$\dfrac{9}{10} + \dfrac{1}{10}$

Contestar: 1

Ejercicio$\PageIndex{4}$

$\dfrac{3}{11} + \dfrac{4}{11}$

Ejercicio$\PageIndex{5}$

$\dfrac{9}{15} + \dfrac{4}{15}$

Contestar: $\dfrac{13}{15}$

Ejercicio$\PageIndex{6}$

$\dfrac{3}{10} + \dfrac{2}{10}$

Ejercicio$\PageIndex{7}$

$\dfrac{5}{12} + \dfrac{7}{12}$

Contestar: 1

Ejercicio$\PageIndex{8}$

$\dfrac{11}{16} - \dfrac{2}{16}$

Ejercicio$\PageIndex{9}$

$\dfrac{3}{16} - \dfrac{3}{16}$

Contestar: 0

Ejercicio$\PageIndex{10}$

$\dfrac{15}{23} - \dfrac{2}{23}$

Ejercicio$\PageIndex{11}$

$\dfrac{1}{6} - \dfrac{1}{6}$

Contestar: 0

Ejercicio$\PageIndex{12}$

$\dfrac{1}{4} + \dfrac{1}{4} + \dfrac{1}{4}$

Ejercicio$\PageIndex{13}$

$\dfrac{3}{11} + \dfrac{1}{11} + \dfrac{5}{11}$

Contestar: $\dfrac{9}{11}$

Ejercicio$\PageIndex{14}$

$\dfrac{16}{20} + \dfrac{1}{20} + \dfrac{2}{20}$

Ejercicio$\PageIndex{15}$

$\dfrac{12}{8} + \dfrac{2}{8} - \dfrac{1}{8}$

Contestar: $\dfrac{1}{2}$

Ejercicio$\PageIndex{16}$

$\dfrac{11}{16} + \dfrac{9}{16} - \dfrac{5}{16}$

Ejercicio$\PageIndex{17}$

$\dfrac{4}{20} - \dfrac{1}{20} + \dfrac{9}{20}$

Contestar: $\dfrac{3}{5}$

Ejercicio$\PageIndex{18}$

$\dfrac{7}{10} - \dfrac{3}{10} + \dfrac{11}{10}$

Ejercicio$\PageIndex{19}$

$\dfrac{16}{5} - \dfrac{1}{5} - \dfrac{2}{5}$

Contestar: $\dfrac{13}{5}$

Ejercicio$\PageIndex{20}$

$\dfrac{21}{35} - \dfrac{17}{35} + \dfrac{31}{35}$

Ejercicio$\PageIndex{21}$

$\dfrac{5}{2} + \dfrac{16}{2} - \dfrac{1}{2}$

Contestar: 10

Ejercicio$\PageIndex{22}$

$\dfrac{1}{18} + \dfrac{3}{18} + \dfrac{1}{18} + \dfrac{4}{18} - \dfrac{5}{18}$

Ejercicio$\PageIndex{23}$

$\dfrac{6}{22} - \dfrac{2}{22} + \dfrac{4}{22} - \dfrac{1}{22} + \dfrac{11}{22}$

Contestar: $\dfrac{9}{11}$

La siguiente regla para la suma y resta de dos fracciones es despreciosa. Mostrar por qué realizando las operaciones usando la regla para los dos problemas siguientes.

Regla despreciosa
Para sumar o restar dos fracciones, basta con sumar o restar los numeradores y colocar este resultado sobre la suma o diferencia de los denominadores.

Ejercicio$\PageIndex{24}$

$\dfrac{3}{10} - \dfrac{3}{10}$

Ejercicio$\PageIndex{25}$

$\dfrac{8}{15} + \dfrac{8}{15}$

Contestar: $\dfrac{16}{30} = \dfrac{8}{15}$(usando la regla despreciosa)

Ejercicio$\PageIndex{26}$

Encuentra la longitud total del tornillo.

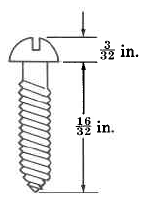
$Un tornillo. La cabeza del tornillo es de tres treinta segundos de pulgada. El eje del tornillo es de dieciséis treinta segundos de pulgada.$

Hace dos meses, una mujer pagó$\dfrac{3}{24}$ un préstamo. Hace un mes, ella pagó$\dfrac{5}{24}$ el préstamo total. Este mes volverá a pagar$\dfrac{5}{24}$ el préstamo total. A fin de mes, ¿cuánto de su préstamo total habrá pagado?

Contestar: $\dfrac{13}{24}$

Ejercicio$\PageIndex{27}$

Encuentra el diámetro interior de la tubería.

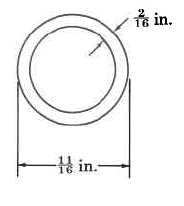
$Una tubería con un espesor de dos dieciseisavos, y un diámetro total de once a dieciseisavos.$

Ejercicios para la revisión

Ejercicio$\PageIndex{28}$

Redondear 2,650 al cien más cercano.

Contestar: 2700

Ejercicio$\PageIndex{29}$

Utilice los números 2, 4 y 8 para ilustrar la propiedad asociativa de la suma.

Ejercicio$\PageIndex{30}$

Encuentra los factores primos de 495.

Contestar: $3^2 \cdot 5 \cdot 11$

Ejercicio$\PageIndex{31}$

Encuentra el valor de$\dfrac{3}{4} \cdot \dfrac{16}{25} \cdot \dfrac{5}{9}$.

Ejercicio$\PageIndex{32}$

$\dfrac{8}{3}$de que numero es$1 \dfrac{7}{9}$?

Contestar: $\dfrac{2}{3}$