5.4: Comparando Fracciones

Última actualización
Guardar como PDF

Page ID: 116654

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

entender el orden de los números y estar familiarizado con los símbolos de agrupación
ser capaz de comparar dos o más fracciones

El orden y los símbolos de la desigualdad

Nuestro sistema de números se llama sistema de números ordenados porque los números en el sistema se pueden colocar en orden de menor a mayor. Esto se ve fácilmente en la línea numérica.

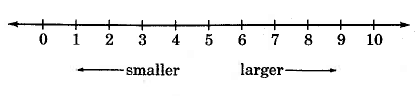
$Una línea numérica que muestra las marcas de 0 a 10. Una flecha apunta hacia la izquierda, etiquetada como más pequeña. Otra flecha apunta a la derecha, etiquetada más grande.$

En la recta numérica, un número que aparece a la derecha de otro número es mayor que ese otro número. Por ejemplo, 5 es mayor que 2 porque 5 se encuentra a la derecha de 2 en la recta numérica. También podemos decir que 2 es menor que 5.

Para que las frases de desigualdad “mayor que” y “menor que” sean más breves, los matemáticos las representan con los símbolos > y <, respectivamente.

Símbolos para Mayor que > y Menor que <
> representa la frase “mayor que”.
< representa la frase “menos que”.

5 > 2 representa “5 es mayor que 2".

2 < 5 representa “2 es menor que 5”.

Comparando Fracciones

Recordemos que la fracción$\dfrac{4}{5}$ indica que tenemos 4 de 5 partes de alguna cantidad entera, y la fracción$\dfrac{3}{5}$ indica que tenemos 3 de 5 partes. Ya que 4 de 5 partes es más de 3 de 5 partes,$\dfrac{4}{5}$ es mayor que$\dfrac{3}{5}$; es decir,

$\dfrac{4}{5} > \dfrac{3}{5}$

Acabamos de observar que cuando dos fracciones tienen el mismo denominador, podemos determinar cuál es mayor comparando los numeradores.

Comparando Fracciones
Si dos fracciones tienen los mismos denominadores, la fracción con el numerador mayor es la fracción mayor.

Así, para comparar los tamaños de dos o más fracciones, solo necesitamos convertir cada una de ellas en fracciones equivalentes que tengan un denominador común. Luego comparamos los numeradores. Es conveniente si el denominador común es la LCD. La fracción con el numerador más grande es la fracción mayor.

Conjunto de Muestras A

Comparar$\dfrac{8}{9}$ y$\dfrac{14}{15}$. Convierte cada fracción en una fracción equivalente con la LCD como denominador. Encuentra la pantalla LCD.

Solución

$\left \{ \begin{array} {rcl} {9} & = & {3^2} \\ {15} & = & {3 \cdot 5} \end{array} \right \} \text{ The LCD } = 3^2 \cdot 5 = 9 \cdot 5 = 45$

$\dfrac{8}{9} = \dfrac{8 \cdot 5}{45} = \dfrac{40}{45}$

$\dfrac{14}{15} = \dfrac{14 \cdot 3}{45} = \dfrac{42}{45}$

Ya que$40 < 42$.

$\dfrac{40}{45} < \dfrac{42}{45}$

Así$\dfrac{8}{9} < \dfrac{14}{15}$.

Conjunto de Muestras A

Escribir$\dfrac{5}{6}$,$\dfrac{7}{10}$, y$\dfrac{13}{15}$ en orden de menor a mayor.

Convierte cada fracción en una fracción equivalente con la LCD como denominador.

Encuentra la pantalla LCD.

Solución

$\left \{ \begin{array} {rcl} {6} & = & {2 \cdot 3} \\ {10} & = & {2 \cdot 5} \\ {15} & = & {3 \cdot 5} \end{array} \right \} \text{ The LCD } = 2 \cdot 3 \cdot 5 = 30$

$\dfrac{5}{6} = \dfrac{5 \cdot 5}{30} = \dfrac{25}{30}$

$\dfrac{7}{10} = \dfrac{7 \cdot 3}{30} = \dfrac{21}{30}$

$\dfrac{13}{15} = \dfrac{13 \cdot 2}{30} = \dfrac{26}{30}$

Ya que$21 < 25 < 26$.

$\dfrac{21}{30} < \dfrac{25}{30} < \dfrac{26}{30}$

$\dfrac{7}{10} < \dfrac{5}{6} < \dfrac{13}{15}$

Escribiendo estos números en orden de menor a mayor, obtenemos$\dfrac{7}{10}$,$\dfrac{5}{6}$,$\dfrac{13}{15}$.

Conjunto de Muestras A

Comparar$8 \dfrac{6}{7}$ y$6 \dfrac{3}{4}$.

Solución

Para comparar números mixtos que tienen diferentes partes de números enteros, solo necesitamos comparar partes de números enteros. Desde 6 < 8,$6 \dfrac{3}{4} < 8 \dfrac{6}{7}$

Conjunto de Muestras A

Comparar$4 \dfrac{5}{8}$ y$4 \dfrac{7}{12}$

Solución

Para comparar números mixtos que tienen el mismo número entero de partes, solo necesitamos comparar partes fraccionarias.

$\left \{ \begin{array} {rcl} {8} & = & {2 \cdot 3} \\ {12} & = & {2^2 \cdot 3} \end{array} \right \} \text{ The LCD } = 2^3 \cdot 3 = 8 \cdot 3 = 24$

$\dfrac{5}{8} = \dfrac{5 \cdot 3}{24} = \dfrac{15}{24}$

$\dfrac{7}{12} = \dfrac{7 \cdot 2}{24} = \dfrac{14}{24}$

Ya que$14 < 15$.

$\dfrac{14}{24} < \dfrac{15}{24}$

$\dfrac{7}{12} < \dfrac{5}{8}$

Por lo tanto,$4 \dfrac{7}{12} < 4 \dfrac{5}{8}$

Conjunto de práctica A

Comparar$\dfrac{3}{4}$ y$\dfrac{4}{5}$

Contestar: $\dfrac{3}{4} < \dfrac{4}{5}$

Conjunto de práctica A

Comparar$\dfrac{9}{10}$ y$\dfrac{13}{15}$

Contestar: $\dfrac{13}{15} < \dfrac{9}{10}$

Conjunto de práctica A

Escribir$\dfrac{13}{16}$,$\dfrac{17}{20}$, y$\dfrac{33}{40}$ en orden de menor a mayor.

Contestar: $\dfrac{13}{16}$,$\dfrac{33}{40}$,$\dfrac{17}{20}$

Conjunto de práctica A

Comparar$11 \dfrac{1}{6}$ y$9 \dfrac{2}{5}$.

Contestar: $9 \dfrac{2}{5} < 11 \dfrac{1}{6}$

Conjunto de práctica A

Comparar$1 \dfrac{9}{14}$ y$1 \dfrac{11}{16}$.

Contestar: $1 \dfrac{9}{14} < 1 \dfrac{11}{16}$

Ejercicios

Organizar cada colección de números en orden de menor a mayor.

Ejercicio$\PageIndex{1}$

$\dfrac{3}{5}$,$\dfrac{5}{8}$

Contestar: $\dfrac{3}{5} < \dfrac{5}{8}$

Ejercicio$\PageIndex{2}$

$\dfrac{1}{6}, \dfrac{2}{7}$

Ejercicio$\PageIndex{3}$

$\dfrac{3}{4}$,$\dfrac{5}{6}$

Contestar: $\dfrac{3}{4} < \dfrac{5}{6}$

Ejercicio$\PageIndex{4}$

$\dfrac{7}{9}, \dfrac{11}{12}$

Ejercicio$\PageIndex{5}$

$\dfrac{3}{8}$,$\dfrac{2}{5}$

Contestar: $\dfrac{3}{8} < \dfrac{2}{5}$

Ejercicio$\PageIndex{6}$

$\dfrac{1}{2}, \dfrac{5}{8}, \(\dfrac{7}{16}$

Ejercicio$\PageIndex{7}$

$\dfrac{1}{2}$,$\dfrac{3}{5}$,$\dfrac{4}{7}$

Contestar: $\dfrac{1}{2} < \dfrac{4}{7} < \dfrac{3}{5}$

Ejercicio$\PageIndex{8}$

$\dfrac{3}{4}, \dfrac{2}{3}, \(\dfrac{5}{6}$

Ejercicio$\PageIndex{9}$

$\dfrac{3}{4}$,$\dfrac{7}{9}$,$\dfrac{5}{4}$

Contestar: $\dfrac{3}{4} < \dfrac{7}{9} < \dfrac{5}{4}$

Ejercicio$\PageIndex{10}$

$\dfrac{7}{8}, \dfrac{15}{16}, \(\dfrac{11}{12}$

Ejercicio$\PageIndex{11}$

$\dfrac{3}{14}$,$\dfrac{2}{7}$,$\dfrac{3}{4}$

Contestar: $\dfrac{3}{14} < \dfrac{2}{7} < \dfrac{3}{4}$

Ejercicio$\PageIndex{12}$

$\dfrac{17}{32}, \dfrac{25}{48}, \(\dfrac{13}{16}$

Ejercicio$\PageIndex{13}$

$5 \dfrac{3}{5}$,$5 \dfrac{4}{7}$

Responder: $5 \dfrac{4}{7} < 5 \dfrac{3}{5}$

Ejercicio$\PageIndex{14}$

$11 \dfrac{3}{16}, 11 \dfrac{1}{12}$

Ejercicio$\PageIndex{15}$

$9 \dfrac{2}{3}$,$9 \dfrac{4}{5}$

Responder: $9 \dfrac{2}{3} < 9 \dfrac{4}{5}$

Ejercicio$\PageIndex{16}$

$7 \dfrac{2}{3}, 8 \dfrac{5}{6}$

Ejercicio$\PageIndex{17}$

$1 \dfrac{9}{16}$,$2 \dfrac{1}{20}$

Responder: $1 \dfrac{9}{16} < 2 \dfrac{1}{20}$

Ejercicio$\PageIndex{18}$

$20 \dfrac{15}{16}, 20 \dfrac{23}{24}$

Ejercicio$\PageIndex{19}$

$2 \dfrac{2}{9}$,$2 \dfrac{3}{7}$

Responder: $2 \dfrac{2}{9} < 2 \dfrac{3}{7}$

Ejercicio$\PageIndex{20}$

$5 \dfrac{8}{13}, 5 \dfrac{9}{20}$

Ejercicios para revisión

Ejercicio$\PageIndex{21}$

Redondear 267,006,428 a los diez millones más cercanos.

Responder: 270,000,000

Ejercicio$\PageIndex{22}$

¿Es el número 82.644 divisible por 2? por 3? por 4?

Ejercicio$\PageIndex{23}$

Convertir$3 \dfrac{2}{7}$ a una fracción impropia.

Responder: $\dfrac{23}{7}$

Ejercicio$\PageIndex{24}$

Encuentra el valor de$\dfrac{5}{6} + \dfrac{3}{10} - \dfrac{2}{5}$

Ejercicio$\PageIndex{25}$

Encuentra el valor de$8 \dfrac{3}{8} + 5 \dfrac{1}{4}$.

Responder: $13 \dfrac{5}{8}$o$\dfrac{109}{8}$