7.4: Por ciento
- Page ID
- 116284
Objetivos de aprendizaje
- comprender la relación entre ratios y porcentajes
- ser capaz de realizar conversiones entre fracciones, decimales y porcentajes
Ratios y porcentajes
Relación, Porcentaje
Definimos una relación como una comparación, por división, de dos números puros o dos números denominados similares. Un número más conveniente para comparar números es 100. Las relaciones en las que un número se compara con 100 se denominan porcentajes. La palabra porcentaje proviene de la palabra latina “per centum”. La palabra “per” significa “para cada” o “para cada”, y la palabra “centum” significa “cien”. Así, tenemos la siguiente definición.
Por ciento significa “por cada cien”, o “por cada cien”.
El símbolo% se utiliza para representar la palabra por ciento.
Conjunto de Muestras A
La relación 26 a 100 se puede escribir como 26%. Leemos 26% como “veintiséis por ciento”.
Conjunto de Muestras A
La relación se\(\dfrac{165}{100}\) puede escribir como 165%.
Leemos el 165% como “ciento sesenta y cinco por ciento”.
Conjunto de Muestras A
El porcentaje 38% se puede escribir como la fracción\(\dfrac{38}{100}\).
Conjunto de Muestras A
El por ciento 210% se puede escribir como la fracción\(\dfrac{210}{100}\) o el número mixto\(2\dfrac{1)}{100}\) o 2.1.
Conjunto de Muestras A
Ya que un dólar es de 100 centavos, 25 centavos es\(\dfrac{25}{100}\) de dólar. Esto implica que 25 centavos es 25% de un dólar.
Conjunto de práctica A
Escribe la relación 16 a 100 como porcentaje.
- Contestar
-
16%
Conjunto de práctica A
Escribe la relación 195 a 100 como porcentaje.
- Contestar
-
195%
Conjunto de práctica A
Escriba el porcentaje 83% como proporción en forma fraccionaria.
- Contestar
-
\(\dfrac{83}{100}\)
Conjunto de práctica A
Escriba el porcentaje 362% como una relación en forma fraccionaria.
- Contestar
-
\(\dfrac{362}{100}\)o\(\dfrac{181}{50}\)
La relación entre fracciones, decimales y porcentajes: hacer conversiones
Dado que un porcentaje es una proporción, y una relación se puede escribir como una fracción, y una fracción se puede escribir como decimal, cualquiera de estas formas se puede convertir a cualquier otra.
Antes de proceder a los problemas en el Conjunto de Muestras B y el Conjunto de Práctica B, resumimos las técnicas de conversión.
| Para convertir una fracción | Para convertir un decimal | Para convertir un porcentaje |
| A un decimal: Divide el numerador por el denominador | A una fracción: Leer el decimal y reducir la fracción resultante | A un decimal: Mueve el punto decimal 2 lugares hacia la izquierda y suelta el símbolo% |
| A un porcentaje: Convierte la fracción primero a un decimal, luego mueve el punto decimal 2 lugares a la derecha y coloca el símbolo%. | A un porcentaje: Mueva el punto decimal 2 lugares a la derecha y coloque el símbolo% | A una fracción: Deja caer el signo% y escribe el número “sobre” 100. Reducir, si es posible. |
Conjunto de Muestras B
Convierte 12% a decimal.
Solución
\(12\% = \dfrac{12}{100} = 0.12\)
Tenga en cuenta que
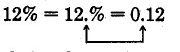
Se deja caer el símbolo% y el punto decimal se mueve 2 lugares hacia la izquierda.
Conjunto de Muestras B
Convertir 0.75 a un por ciento.
Solución
\(0.75 = \dfrac{75}{100} = 75\%\)
Tenga en cuenta que
Se fija el símbolo% y el punto decimal se mueve 2 unidades a la derecha.
Conjunto de Muestras B
Convertir\(\dfrac{3}{5}\) a un porcentaje.
Solución
Vemos en Ejemplo anterior que podemos convertir un decimal a un porcentaje. También sabemos que podemos convertir una fracción a un decimal. Así, podemos ver que si primero convertimos la fracción a un decimal, entonces podemos convertir el decimal a un porcentaje.
\(\dfrac{3}{5} \to \begin{array} {r} {.6} \\ {5\overline{)3.0}} \\ {\underline{3\ 0}} \\ {0} \end{array} \text{ or } \dfrac{3}{5} = 0.6 = \dfrac{6}{10} = \dfrac{60}{100} = 60\%\)
Conjunto de Muestras B
Convierte 42% en una fracción.
Solución
\(42\% = \dfrac{42}{100} = \dfrac{21}{50}\)
o
\(42\% = 0.42 = \dfrac{42}{100} = \dfrac{21}{50}\)
Set de práctica B
Convierte 21% a decimal.
- Contestar
-
0.21
Set de práctica B
Convierte 461% a decimal.
- Contestar
-
4.61
Set de práctica B
Convertir 0.55 a un por ciento.
- Contestar
-
55%
Set de práctica B
Convertir 5.64 a un por ciento.
- Contestar
-
564%
Set de práctica B
Convertir\(\dfrac{3}{20}\) a un porcentaje.
- Contestar
-
15%
Set de práctica B
Convertir\(\dfrac{11}{8}\) a un porcentaje.
- Contestar
-
137.5%
Set de práctica B
Convertir\(\dfrac{3}{11}\) a un porcentaje.
- Contestar
-
\(27.\overline{27}\)%
Ejercicios
Para los siguientes 12 problemas, convierta cada decimal a un porcentaje.
Ejercicio\(\PageIndex{1}\)
0.25
- Contestar
-
25%
Ejercicio\(\PageIndex{2}\)
0.36
Ejercicio\(\PageIndex{3}\)
0.48
- Contestar
-
48%
Ejercicio\(\PageIndex{4}\)
0.343
Ejercicio\(\PageIndex{5}\)
0.771
- Contestar
-
77.1%
Ejercicio\(\PageIndex{6}\)
1.42
Ejercicio\(\PageIndex{7}\)
2.58
- Contestar
-
258%
Ejercicio\(\PageIndex{8}\)
4.976
Ejercicio\(\PageIndex{9}\)
16.1814
- Contestar
-
1,618.14%
Ejercicio\(\PageIndex{10}\)
533.01
Ejercicio\(\PageIndex{11}\)
2
- Contestar
-
200%
Ejercicio\(\PageIndex{12}\)
14
Para los siguientes 10 problemas, convierta cada porcentaje a un decimal.
Ejercicio\(\PageIndex{13}\)
15%
- Contestar
-
0.15
Ejercicio\(\PageIndex{14}\)
43%
Ejercicio\(\PageIndex{15}\)
16.2%
- Contestar
-
0.162
Ejercicio\(\PageIndex{16}\)
53.8%
Ejercicio\(\PageIndex{17}\)
5.05%
- Contestar
-
0.0505
Ejercicio\(\PageIndex{18}\)
6.11%
Ejercicio\(\PageIndex{19}\)
0.78%
- Contestar
-
0.0078
Ejercicio\(\PageIndex{20}\)
0.88%
Ejercicio\(\PageIndex{21}\)
0.09%
- Contestar
-
0.0009
Ejercicio\(\PageIndex{22}\)
0.001%
Para los siguientes 14 problemas, convierta cada fracción a un porcentaje.
Ejercicio\(\PageIndex{23}\)
\(\dfrac{1}{5}\)
- Contestar
-
20%
Ejercicio\(\PageIndex{24}\)
\(\dfrac{3}{5}\)
Ejercicio\(\PageIndex{25}\)
\(\dfrac{5}{8}\)
- Contestar
-
62.5%
Ejercicio\(\PageIndex{26}\)
\(\dfrac{1}{16}\)
Ejercicio\(\PageIndex{27}\)
\(\dfrac{7}{25}\)
- Contestar
-
28%
Ejercicio\(\PageIndex{28}\)
\(\dfrac{16}{45}\)
Ejercicio\(\PageIndex{29}\)
\(\dfrac{27}{55}\)
- Contestar
-
\(49.\overline{09}\)%
Ejercicio\(\PageIndex{30}\)
\(\dfrac{15}{8}\)
Ejercicio\(\PageIndex{31}\)
\(\dfrac{41}{25}\)
- Contestar
-
164%
Ejercicio\(\PageIndex{32}\)
\(6 \dfrac{4}{5}\)
Ejercicio\(\PageIndex{33}\)
\(9 \dfrac{9}{20}\)
- Responder
-
945%
Ejercicio\(\PageIndex{34}\)
\(\dfrac{1}{200}\)
Ejercicio\(\PageIndex{35}\)
\(\dfrac{6}{11}\)
- Responder
-
\(54.\overline{54}\)%
Ejercicio\(\PageIndex{36}\)
\(\dfrac{35}{27}\)
Para los siguientes 14 problemas, convierta cada porcentaje a una fracción.
Ejercicio\(\PageIndex{37}\)
80%
- Responder
-
\(\dfrac{4}{5}\)
Ejercicio\(\PageIndex{38}\)
60%
Ejercicio\(\PageIndex{37}\)
25%
- Responder
-
\(\dfrac{1}{4}\)
Ejercicio\(\PageIndex{38}\)
75%
Ejercicio\(\PageIndex{37}\)
65%
- Responder
-
\(\dfrac{13}{20}\)
Ejercicio\(\PageIndex{38}\)
18%
Ejercicio\(\PageIndex{37}\)
12.5%
- Responder
-
\(\dfrac{1}{8}\)
Ejercicio\(\PageIndex{38}\)
37.5%
Ejercicio\(\PageIndex{37}\)
512.5%
- Responder
-
\(\dfrac{41}{8}\)o\(5 \dfrac{1}{8}\)
Ejercicio\(\PageIndex{38}\)
937.5%
Ejercicio\(\PageIndex{37}\)
\(9.\overline{9}\)%
- Responder
-
\(\dfrac{1}{10}\)
Ejercicio\(\PageIndex{38}\)
\(55.\overline{5}\)%
Ejercicio\(\PageIndex{37}\)
\(22.\overline{2}\)%
- Responder
-
\(\dfrac{2}{9}\)
Ejercicio\(\PageIndex{38}\)
\(63.\overline{6}\)%
Ejercicios para revisión
Ejercicio\(\PageIndex{39}\)
Encuentra el cociente. \(\dfrac{40}{54} \div 8 \dfrac{7}{21}\).
- Responder
-
\(\dfrac{2}{9}\)
Ejercicio\(\PageIndex{40}\)
\(\dfrac{3}{8}\)de que numero es\(2\dfrac{2}{3}\)?
Ejercicio\(\PageIndex{41}\)
Encuentra el valor de\(\dfrac{28}{15} + \dfrac{7}{10} - \dfrac{5}{12}\).
- Responder
-
\(\dfrac{129}{60}\)o\(2 \dfrac{9}{60} = 2 \dfrac{3}{20}\)
Ejercicio\(\PageIndex{42}\)
Ronda 6.99997 a las diez milésimas más cercanas.
Ejercicio\(\PageIndex{43}\)
En un mapa, 3 pulgadas representan 40 millas. ¿Cuántas pulgadas representan 480 millas?
- Responder
-
36 pulgadas


