10.7: Resumen de conceptos clave

Última actualización
Guardar como PDF

Page ID: 116563

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Resumen de Key Concepts

Variables y constantes
Una variable es una letra o símbolo que representa cualquier miembro de un conjunto de dos o más números. Una constante es una letra o símbolo que representa un número específico. Por ejemplo, la letra griega$\pi$ (pi) representa la constante 3.14159..

La línea numérica real
La línea numérica real nos permite mostrar visualmente algunos de los números en los que estamos interesados.

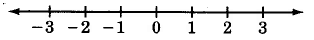
$Una línea numérica con marcas hash de -3 a 3.$

Coordenada y Gráfica
El número asociado a un punto en la recta numérica se denomina coordenada del punto. El punto asociado a un número se llama la gráfica del número.

Número real
Un número real es cualquier número que sea la coordenada de un punto en la línea numérica real.

Tipos de números reales
El conjunto de números reales tiene muchos subconjuntos. Los que más nos interesan son:
Los números naturales: {1, 2, 3, 4,.}
Los números enteros: {0, 1, 2, 3, 4,.}
Los enteros: {.., -3, -2, -1,0, 1, 2, 3,.}
Los números racionales: {Todos los números que se pueden expresar como el cociente de dos enteros.}

Números positivos y negativos
Un número se denota como positivo si va precedido directamente por un signo más (+) o ningún signo en absoluto. Un número se denota como negativo si va precedido directamente por un signo menos (—).

Opuestos
Los opuestos son números que están a la misma distancia de cero en la recta numérica pero que tienen signos opuestos. Los números$a$ y$-a$ son opuestos.

Propiedad Doble Negativa ([link])
$-(-a) = a$

Valor Absoluto (Geométrico)
El valor absoluto de un número$a$, denotado$|a|$, es la distancia desde$a$ hasta 0 en esta recta numérica.

Valor Absoluto (Algebraico) ([link])
$|a| = \begin{cases} a, \text{ if } a \ge 0 \\ -a, \text{ if } a < 0 \end{cases}$

Suma de números firmados
Para sumar dos números con

como signos, sumar los valores absolutos de los números y asociar con la suma el signo común.
a diferencia de los signos, restar el valor absoluto menor del valor absoluto mayor y asociar con la diferencia el signo del valor absoluto mayor.

Adición con cero
$0 + \text{(any number) = that particular number.}$

Identidad aditiva
Dado que agregar 0 a cualquier número real deja ese número sin cambios, 0 se denomina identidad aditiva.

Definición de resta
$a - b = a + (-b)$

Resta de números firmados
Para realizar la resta$a - b$, suma lo contrario de$b$ a$a$, es decir, cambiar el signo de$b$ y seguir las reglas de suma.

Multiplicación y División de Números Signos ([link])
(+) (+) = (+)$\dfrac{(+)}{(+)} = (+)$$\dfrac{(+)}{(-)} = (-)$
(-) (-) = (+)
(+) (-) = (-)$\dfrac{(-)}{(-)} = (+)$$\dfrac{(-)}{(+)} = (-)$
(-) (+) = (-)