10.6: Multiplicación y división de números firmados

Última actualización
Guardar como PDF

Page ID: 116547

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

ser capaz de multiplicar y dividir números firmados
ser capaz de multiplicar y dividir números firmados usando una calculadora

Multiplicación de números firmados

Consideremos primero, el producto de dos números positivos. Multiplicar:$3 \cdot 5$.

$3 \cdot 5$significa$5 + 5 + 5 = 15$

Esto sugiere que (En cursos posteriores de matemáticas, la palabra “sugiere” se convierte en la palabra “prueba”. Un ejemplo no prueba un reclamo. Las pruebas matemáticas se construyen para validar un reclamo para todos los casos posibles.)

$\text{(positive number)} \cdot \text{(positive number)} = \text{(positive number)}$

Más brevemente,

(+) (+) = (+)

Ahora considere el producto de un número positivo y un número negativo. Multiplicar: (3) (-5)

(3) (-5) significa (-5) + (-5) + (-5) = -15

Esto sugiere que

$\text{(positive number)} \cdot \text{(negative number)} = \text{(negative number)}$

Más brevemente,

(+) (-) = (-)

Por la propiedad conmutativa de la multiplicación, obtenemos

$\text{(negative number)} \cdot \text{(positive number)} = \text{(negative number)}$

Más brevemente,

(-) (+) = (-)

El signo del producto de dos números negativos se puede sugerir después de observar la siguiente ilustración.

Multiplica -2 por, respectivamente, 4, 3, 2, 1, 0, -1, -2, -3, -4.

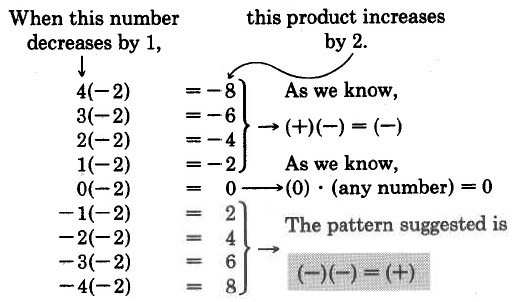
$Una lista de ecuaciones. 4 veces negativo 2 es igual a negativo 8. 3 veces negativo 2 es igual a negativo 6. 2 veces negativo 2 es igual negativo 4. 1 veces negativo 2 es igual a negativo 2. Por todo esto, se enumera al costado la siguiente etiqueta: Como sabemos, un negativo por un positivo equivale a un negativo. La lista continúa. 0 veces negativo 2 es igual a 0. La siguiente etiqueta aparece listada a un lado: Como sabemos, 0 veces cualquier número es igual a 0. La lista continúa más. Negativo 1 veces negativo 2 es igual a 2. Negativo 2 veces negativo 2 es igual a 4. Negativo 3 veces negativo 2 es igual a 6. Negativo 4 veces negativo 2 es igual a 8. La siguiente etiqueta se enumera a un lado: El patrón sugerido es un negativo veces un negativo es igual a un positivo. Para toda la lista, la etiqueta en la parte superior dice: cuando este número disminuye en 1, el primer factor en cada problema de multiplicación, el producto aumenta en 2.$

Tenemos las siguientes reglas para multiplicar números firmados.

Reglas para Multiplicar Números Signados
Multiplicar números firmados:

Para multiplicar dos números reales que tengan el mismo signo, multiplique sus valores absolutos. El producto es positivo.
(+) (+) = (+)
(-) (-) = (+)
Para multiplicar dos números reales que tengan signos opuestos, multiplique sus valores absolutos. El producto es negativo.
(+) (-) = (-)
(-) (+) = (-)

Conjunto de Muestras A

Encuentra los siguientes productos.

$8 \cdot 6$

Solución

$\begin{array} {ccl} {|8|} & = & {8} \\ {|6|} & = & {6} \end{array} \big \}$Multiplique estos valores absolutos.

$8 \cdot 6 = 48$

Dado que los números tienen el mismo signo, el producto es positivo.

Así,$8 \cdot 6 = +48$, o$8 \cdot 6 = 48$.

Conjunto de Muestras A

(-8) (-6)

Solución

$\begin{array} {ccl} {|-8|} & = & {8} \\ {|-6|} & = & {6} \end{array} \big \}$Multiplique estos valores absolutos.

$8 \cdot 6 = 48$

Dado que los números tienen el mismo signo, el producto es positivo.

Así,$(-8)(-6) = +48$, o$(-8)(-6) = 48$.

Conjunto de Muestras A

(-4) (7)

Solución

$\begin{array} {ccl} {|-4|} & = & {4} \\ {|7|} & = & {7} \end{array} \big \}$Multiplique estos valores absolutos.

$4 \cdot 7 = 28$

Dado que los números tienen signos opuestos, el producto es negativo.

Así, (-4) (7) = -28.

Conjunto de Muestras A

6 (-3)

Solución

$\begin{array} {ccl} {|6|} & = & {6} \\ {|-3|} & = & {3} \end{array} \big \}$Multiplique estos valores absolutos.

$6 \cdot 3 = 18$

Dado que los números tienen signos opuestos, el producto es negativo.

Así, 6 (-3) = -18.

Conjunto de práctica A

Encuentra los siguientes productos.

3 (-8)

Responder: -24

Conjunto de práctica A

4 (16)

Responder: 64

Conjunto de práctica A

(-6) (-5)

Responder: 30

Conjunto de práctica A

(-7) (-2)

Responder: 14

Conjunto de práctica A

(-1) (4)

Responder: -4

Conjunto de práctica A

(-7) 7

Responder: -49

División de Números Firmados

Para determinar los signos en un problema de división, recuerde que

$\dfrac{12}{3} = 4$desde$12 = 3 \cdot 4$

Esto sugiere que

$\dfrac{(+)}{(+)} = (+)$

$\dfrac{(+)}{(+)} = (+)$ya que (+) = (+) (+)

¿Qué es$\dfrac{12}{-3}$?

12 = (-3) (-4) sugiere eso$\dfrac{12}{-3} = -4$. Es decir,

$\dfrac{(+)}{(-)} = (-)$

(+) = (-) (-) sugiere que$\dfrac{(+)}{(-)} = (-)$

¿Qué es$\dfrac{-12}{3}$?

-12 = (3) (-4) sugiere que$\dfrac{-12}{3} = -4$. Es decir,

$\dfrac{(-)}{(+)} = (-)$

(-) = (+) (-) sugiere que$\dfrac{(-)}{(+)} = (-)$

¿Qué es$\dfrac{-12}{-3}$?

-12 = (-3) (4) sugiere eso$\dfrac{-12}{-3} = 4$. Es decir,

$\dfrac{(-)}{(-)} = (+)$

(-) = (-) (+) sugiere que$\dfrac{(-)}{(-)} = (+)$

Tenemos las siguientes reglas para dividir números firmados.

Reglas para dividir números firmados
Dividir números firmados:

Para dividir dos números reales que tengan el mismo signo, dividir sus valores absolutos. El cociente es positivo.
$\dfrac{(+)}{(+)} = (+)\dfrac{(-)}{(-)} = (+)$
Para dividir dos números reales que tienen signos opuestos, dividir sus valores absolutos. El cociente es negativo.
$\dfrac{(-)}{(+)} = (-)\dfrac{(+)}{(-)} = (-)$

Conjunto de Muestras B

Encuentra los siguientes cocientes.

$\dfrac{-10}{2}$

Solución

$\begin{array} {ccc} {|-10|} & = & {10} \\ {|2|} & = & {2} \end{array} \big \}$Dividir estos valores absolutos.

$\dfrac{10}{2} = 5$

Dado que los números tienen signos opuestos, el cociente es negativo.

Así$\dfrac{-10}{2} = -5$.

Conjunto de Muestras B

$\dfrac{-35}{-7}$

Solución

$\begin{array} {ccc} {|-35|} & = & {35} \\ {|-7|} & = & {7} \end{array} \big \}$Dividir estos valores absolutos.

$\dfrac{35}{7} = 5$

Dado que los números tienen los mismos signos, el cociente es positivo.

Así$\dfrac{-35}{-7} = 5$.

Conjunto de Muestras B

$\dfrac{18}{-9}$

Solución

$\begin{array} {ccc} {|18|} & = & {18} \\ {|-9|} & = & {9} \end{array} \big \}$Dividir estos valores absolutos.

$\dfrac{18}{9} = 2$

Dado que los números tienen signos opuestos, el cociente es negativo.

Así$\dfrac{18}{-9} = -2$.

Set de práctica B

Encuentra los siguientes cocientes.

$\dfrac{-24}{-6}$

Responder: 4

Set de práctica B

$\dfrac{30}{-5}$

Responder: -6

Set de práctica B

$\dfrac{-54}{27}$

Responder: -2

Set de práctica B

$\dfrac{51}{17}$

Responder: 3

Conjunto de Muestras C

Encuentra el valor de$\dfrac{-6(4 - 7) - 2(8 - 9)}{-(4 + 1) + 1}$.

Solución

Usando el orden de operaciones y lo que sabemos sobre los números firmados, obtenemos,

$\begin{array} {rcl} {\dfrac{-6(4 - 7) - 2(8 - 9)}{-(4 + 1) + 1}} & = & {\dfrac{-6(-3) - 2(-1)}{-(5) + 1}} \\ {} & = & {\dfrac{18 + 2}{-5 + 1}} \\ {} & = & {\dfrac{20}{-4}} \\ {} & = & {-5} \end{array}$

Set de práctica C

Encuentra el valor de$\dfrac{-5(2 - 6) - 4(-8 - 1)}{2(3 - 10) - 9(-2)}$.

Responder: 14

Calculadoras

Calculadoras con el

$Una caja con un signo más y menos.$

se puede utilizar para multiplicar y dividir números firmados.

Conjunto de Muestras D

Usa una calculadora para encontrar cada cociente o producto.

$(-186) \cdot (-43)$

Solución

Dado que este producto implica un$\text{(negative)} \cdot \text{(negative)}$, sabemos que el resultado debe ser un número positivo. Ilustraremos esto en la calculadora.

		Lee en pantalla
Tipo	186	186
Prensa	$Una caja con un signo más y menos.$	-186
Prensa	$\times$	-186
Tipo	43	43
Prensa	$Una caja con un signo más y menos.$	-43
Prensa	=	7998

Así,$(-186) \cdot (-43) = 7,998$

Conjunto de Muestras D

$\dfrac{158.64}{-54.3}$. Redondear a una posición decimal.

Solución

Dado que este producto implica un$\text{(negative)} \cdot \text{(negative)}$, sabemos que el resultado debe ser un número positivo. Ilustraremos esto en la calculadora.

		Lee en pantalla
Tipo	158.64	158.64
Prensa	$\div$	158.64
Tipo	54.3	54.3
Prensa	$Una caja con un signo más y menos.$	-54.3
Prensa	=	-2.921546961

Redondeando a un decimal obtenemos -2.9.

Set de Práctica D

Usa una calculadora para encontrar cada valor.

$(-51.3) \cdot (-21.6)$

Responder: 1,108.08

Set de Práctica D

$-2.5746 \div -2.1$

Responder: 1.226

Set de Práctica D

$(0.006) \cdot (-0.241)$. Redondear a tres decimales.

Responder: -0.001

Ejercicios

Encuentra el valor de cada uno de los siguientes. Usa una calculadora para verificar cada resultado.

Ejercicio$\PageIndex{1}$

(-2) (-8)

Responder: 16

Ejercicio$\PageIndex{2}$

(-3) (-9)

Ejercicio$\PageIndex{3}$

(-4) (-8)

Responder: 32

Ejercicio$\PageIndex{4}$

(-5) (-2)

Ejercicio$\PageIndex{5}$

(3) (-12)

Contestar: -36

Ejercicio$\PageIndex{6}$

(4) (-18)

Ejercicio$\PageIndex{7}$

(10) (-6)

Contestar: -60

Ejercicio$\PageIndex{8}$

(-6) (4)

Ejercicio$\PageIndex{9}$

(-2) (6)

Contestar: -12

Ejercicio$\PageIndex{10}$

(-8) (7)

Ejercicio$\PageIndex{11}$

$\dfrac{21}{7}$

Contestar: 3

Ejercicio$\PageIndex{12}$

$\dfrac{42}{6}$

Ejercicio$\PageIndex{13}$

$\dfrac{-39}{3}$

Contestar: -13

Ejercicio$\PageIndex{14}$

$\dfrac{-20}{10}$

Ejercicio$\PageIndex{15}$

$\dfrac{-45}{-5}$

Contestar: 9

Ejercicio$\PageIndex{16}$

$\dfrac{-16}{-8}$

Ejercicio$\PageIndex{17}$

$\dfrac{25}{-5}$

Contestar: -5

Ejercicio$\PageIndex{18}$

$\dfrac{36}{-4}$

Ejercicio$\PageIndex{19}$

8 - (-3)

Contestar: 11

Ejercicio$\PageIndex{20}$

14 - (-20)

Ejercicio$\PageIndex{21}$

20 - (-8)

Contestar: 28

Ejercicio$\PageIndex{22}$

(-4) - (-1)

Ejercicio$\PageIndex{23}$

0 - 4

Contestar: -4

Ejercicio$\PageIndex{24}$

0 - (-1)

Ejercicio$\PageIndex{25}$

-6 + 1 - 7

Contestar: -12

Ejercicio$\PageIndex{26}$

15 - 12 - 20

Ejercicio$\PageIndex{27}$

1 - 6 - 7 + 8

Contestar: -4

Ejercicio$\PageIndex{28}$

2 + 7 - 10 + 2

Ejercicio$\PageIndex{29}$

3 (4 - 6)

Contestar: -6

Ejercicio$\PageIndex{30}$

8 (5 - 12)

Ejercicio$\PageIndex{31}$

-3 (1 - 6)

Contestar: 15

Ejercicio$\PageIndex{32}$

-8 (4 - 12) + 2

Ejercicio$\PageIndex{33}$

-4 (1 - 8) + 3 (10 - 3)

Contestar: 49

Ejercicio$\PageIndex{34}$

-9 (0 - 2) + 4 (8 - 9) + 0 (-3)

Ejercicio$\PageIndex{35}$

6 (-2 - 9) - 6 (2 + 9) + 4 (-1 - 1)

Contestar: -140

Ejercicio$\PageIndex{36}$

$\dfrac{3(4 + 1) - 2 (5)}{-2}$

Ejercicio$\PageIndex{37}$

$\dfrac{4(8 + 1) - 3 (-2)}{-4 - 2}$

Contestar: -7

Ejercicio$\PageIndex{38}$

$\dfrac{-1(3 + 2) + 5}{-1}$

Ejercicio$\PageIndex{39}$

$\dfrac{-3(4 - 2) + (-3)(-6)}{-4}$

Contestar: -3

Ejercicio$\PageIndex{40}$

-1 (4 + 2)

Ejercicio$\PageIndex{41}$

-1 (6 - 1)

Contestar: -5

Ejercicio$\PageIndex{42}$

- (8 + 21)

Ejercicio$\PageIndex{43}$

- (8 - 21)

Contestar: 13

Ejercicios para la revisión

Ejercicio$\PageIndex{44}$

Utilice el orden de las operaciones para simplificar$(5^2 + 3^2 + 2) \div 2^2$.

Ejercicio$\PageIndex{45}$

Hallar$\dfrac{3}{8}$ de$\dfrac{32}{9}$.

Contestar: $\dfrac{4}{3} = 1 \dfrac{1}{3}$

Ejercicio$\PageIndex{46}$

Escribe este número en forma decimal usando dígitos: “cincuenta y dos tres milésimas”

Ejercicio$\PageIndex{47}$

La relación de cloro a agua en una solución es de 2 a 7. ¿Cuántos mL de agua hay en una solución que contiene 15 mL de cloro?

Contestar: $52 \dfrac{1}{2}$

Ejercicio$\PageIndex{48}$

Realizar la resta -8 - (-20)