11.3: Resolviendo Ecuaciones de la Forma x + a = b y x - a = b

Última actualización
Guardar como PDF

Page ID: 116344

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

entender el significado y la función de una ecuación
entender lo que se entiende por la solución a una ecuación
ser capaz de resolver ecuaciones de la forma$x + a = b$ y$x - a = b$

Ecuaciones

Ecuación
Una ecuación es una declaración de que dos expresiones algebraicas son iguales.

Los siguientes son ejemplos de ecuaciones:

$\begin{array} {c} {\underbrace{x + 6}_{\text{This}}} & = & {\underbrace{10}_{\text{This}}} \\ {^\text{expression}} & ^= & {^\text{expression}} \end{array}$$\begin{array} {c} {\underbrace{x - 4}_{\text{This}}} & = & {\underbrace{-11}_{\text{This}}} \\ {^\text{expression}} & ^= & {^\text{expression}} \end{array}$$\begin{array} {c} {\underbrace{3y - 5}_{\text{This}}} & = & {\underbrace{-2 + 2y}_{\text{This}}} \\ {^\text{expression}} & ^= & {^\text{expression}} \end{array}$

Observe que$x + 6$$x - 4$,, y no$3y - 5$ son ecuaciones. Son expresiones. No son ecuaciones porque no hay afirmación de que cada una de estas expresiones sea igual a otra expresión.

Soluciones y Ecuaciones Equivalentes

Ecuaciones condicionales
La verdad de algunas ecuaciones está condicionada al valor elegido para la variable. Tales ecuaciones se llaman ecuaciones condicionales. Hay dos tipos adicionales de ecuaciones. Se examinan en cursos de álgebra, por lo que no los consideraremos ahora.

Soluciones y Resolución de una Ecuación
El conjunto de valores que, al ser sustituidos por las variables, hacen que la ecuación sea verdadera, se denominan las soluciones de la ecuación.
Se ha resuelto una ecuación cuando se han encontrado todas sus soluciones.

Conjunto de Muestras A

Verificar que 3 sea una solución para$x + 7 = 10$.

Solución

Cuando$x = 3$,

se convierte$\begin{array} {rcll} {x + 7} & = & {10} & {} \\ {3 + 7} & = & {10} & {} \\ {10} & = & {10} & {\text{which is a } true \text{ statement, verifying that}} \\ {} & & {} & {\text{3 is a solution to } x + 7 = 10} \end{array}$

Conjunto de Muestras A

Verificar que -6 sea una solución para$5y + 8 = -22$.

Solución

Cuando$y = -6$,

se convierte$\begin{array} {rcll} {5y + 8} & = & {-22} & {} \\ {5(-6) + 8} & = & {-22} & {} \\ {-30 + 8} & = & {-22} & {} \\ {-22} & = & {-22} & {\text{which is a } true \text{ statement, verifying that}} \\ {} & & {} & {\text{-6 is a solution to } 5y + 8 = -22} \end{array}$

Conjunto de Muestras A

Verificar que 5 no sea una solución para$a - 1 = 2a + 3$.

Solución

Cuando$a = 5$,

se convierte$\begin{array} {rcll} {a - 1} & = & {2a + 3} & {} \\ {5 - 1} & = & {2 \cdot 5 + 3} & {} \\ {5 - 1} & = & {10 + 3} & {} \\ {4} & = & {13} & {\text{a } false \text{ statement, verifying that 5}} \\ {} & & {} & {\text{is not a solution to } a - 1 = 2a + 3} \end{array}$

Conjunto de Muestras A

Verificar que -2 sea una solución para$3m - 2 = -4m - 16$.

Solución

Cuando$m = -2$,

se convierte$\begin{array} {rcll} {3m - 2} & = & {-4m - 16} & {} \\ {3(-2) - 2} & = & {-4(-2) - 16} & {} \\ {-6 - 2} & = & {8 - 16} & {} \\ {-8} & = & {-8} & {\text{which is a } true \text{ statement, verifying that}} \\ {} & & {} & {\text{-2 is a solution to } 3m - 2 = -4m - 16} \end{array}$

Conjunto de práctica A

Verificar que 5 sea una solución para$m + 6 = 11$.

Contestar

Sustituir 5 en$m + 6 = 11$.

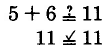
$¿5 más 6 equivale a 11? Sí.$

Así, 5 es una solución.

Conjunto de práctica A

Verifique que −5 sea una solución para$2m - 4 = -14$.

Contestar

Sustituye -5 en$2m - 4 = -14$.

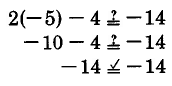
$hace 2 tiempo negativo 5 menos 4 igual negativo 14? Sí.$

Así, -5 es una solución.

Conjunto de práctica A

Verificar que 0 sea una solución para$5x + 1 = 1$.

Contestar

Sustituir 0 en$5x + 1 = 1$.

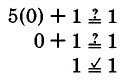
$¿5 veces cero más uno es igual a 1? Sí.$

Así, 0 es una solución.

Conjunto de práctica A

Verificar que 3 no sea una solución para$-3y + 1 = 4y + 5$.

Contestar

Sustituir 3 en$-3y + 1 = 4y + 5$.

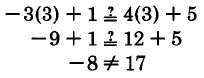
$¿El negativo 3 veces 3 más 1 equivale a 4 veces 3 más 5? No.$

Así, 3 no es una solución.

Conjunto de práctica A

Verificar que -1 sea una solución para$6m - 5 + 2m = 7m - 6$.

Contestar

Sustituir -1 en$6m - 5 + 2m = 7m - 6$.

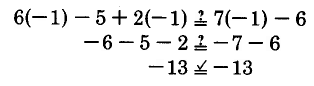
$¿6 veces negativo 1 menos 5 más 2 veces negativo 1 igual 7 veces negativo 1 menos 6? Sí.$

Así, -1 es una solución.

Ecuaciones Equivalentes
Algunas ecuaciones tienen precisamente la misma colección de soluciones. Tales ecuaciones se denominan ecuaciones equivalentes. Por ejemplo,$x - 5 = -1, x + 7 = 11,$ y$x = 4$ son todas ecuaciones equivalentes ya que la única solución para cada una es$x = 4$. (¿Puedes verificar esto?)

Resolviendo Ecuaciones

Sabemos que el signo igual de una ecuación indica que el número representado por la expresión en el lado izquierdo es el mismo que el número representado por la expresión en el lado derecho.

Este número	es lo mismo que	este número
$\downarrow$	$\downarrow$	$\downarrow$
$x$	=	4
$x + 7$	=	11
$x - 5$	=	-1

Sumación/resta Propiedad de igualdad
A partir de esto, podemos sugerir la propiedad de sución/resta de igualdad.
Dada cualquier ecuación,

Podemos obtener una ecuación equivalente sumando el mismo número a ambos lados de la ecuación.
Podemos obtener una ecuación equivalente restando el mismo número de ambos lados de la ecuación.

La idea detrás de la resolución de ecuaciones
La idea detrás de la resolución de ecuaciones es aislar la variable en un lado de la ecuación. Los signos de operación (+, -,$\cdot$,$\div$) se utilizan para asociar dos números. Por ejemplo, en la expresión$5 + 3$, los números 5 y 3 están asociados por adición. Una asociación se puede deshacer realizando la operación opuesta. La propiedad de sución/resta de igualdad se puede utilizar para deshacer una asociación que se realiza por suma o resta.

La resta se utiliza para deshacer una suma.

La suma se utiliza para deshacer una resta.

El procedimiento se ilustra en los problemas de [link].

Conjunto de Muestras B

Utilice la propiedad de sución/resta de igualdad para resolver cada ecuación.

$x + 4 = 6$.

Solución

4 se asocia con$x$ por adición. Deshacer la asociación restando 4 de ambos lados.

$x + 4 - 4 = 6 - 4$

$x + 0 =2$

$x = 2$

Comprobar: Cuando$x = 2$,$x + 4$ se convierte

$Hace 2 + 4 = 6? Sí.$

La solución a$x + 4 = 6$ es$x = 2$.

Conjunto de Muestras B

$m - 8 = 5$.

Solución

8 se asocia con$m$ por resta. Deshacer la asociación agregando 8 a ambos lados.

$m - 8 + 8 = 5 + 8$

$m + 0 = 13$

$m = 13$

Comprobar: Cuando$m = 13$,

se convierte

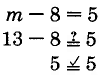
$m - 8 = 5. Después de sustituir, ¿13 - 8 = 5? Sí.$
una declaración verdadera.

La solución a$m - 8 = 5$ es$m = 13$.

Conjunto de Muestras B

$-3 - 5 = y - 2 + 8$.

Solución

Antes de usar la propiedad de sución/resta, debemos simplificar lo más posible.

$-3 - 5 = y - 2 + 8$.

$-8 = y + 6$

6 se asocia con$y$ por adición. Deshacer la asociación restando 6 de ambos lados.

$-8 - 6 = y + 6 - 6$

$-14 = y + 0$

$-14 = y$

Esto equivale a$y = -14$.

Comprobar: Cuando$y = -14$,

$-3 - 5 = y - 2 + 8$

se convierte

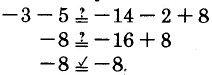
$¿El negativo 3 menos 5 es igual a negativo 14 menos 2 más 8? Sí.$

una declaración verdadera.

La solución a$-3 - 5 = y - 2 + 8$ es$y = -14$.

Conjunto de Muestras B

$-5a + 1 + 6a = -2$.

Solución

Comience simplificando el lado izquierdo de la ecuación.

$\underbrace{-5a + 1 + 6a}_{-5 + 6 = 1} = -2$

$a + 1 = -2$1 se asocia con aa por adición. Deshacer la asociación restando 1 de ambos lados.

$a + 1 - 1 = -2 - 1$

$a + 0 = -3$

$a = -3$

Comprobar: Cuando$a = -3$,

$-5a + 1 + 6a = -2$

se convierte

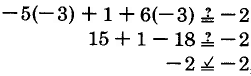
$¿Negativo 5 veces negativo 3 más 1 más 6 veces negativo 3 igual negativo 2? Sí.$
una declaración verdadera.

La solución a$-5a + 1 + 6a = -2$ es$a = -3$.

Conjunto de Muestras B

$7k - 4 = 6k + 1$.

Solución

En esta ecuación, la variable aparece en ambos lados. Tenemos que aislarlo por un lado. Aunque podemos elegir cualquiera de los lados, será más conveniente elegir el lado con el coeficiente mayor. Dado que 8 es mayor que 6, aislaremos$k$ en el lado izquierdo.

$7 k - 4 = 6k + 1$Ya que$6k$ representa$+6k$, restar$6k$ de cada lado.

$\underbrace{7 k - 4 - 6k}_{7 - 6 = 1} = \underbrace{6k + 1 - 6k}_{6 - 6 = 0}$

$k - 4 = 1$4 se asocia con$k$ por resta. Deshacer la asociación agregando 4 a ambos lados.

\ (k - 4 + 4 = 1 + 4\ 0

$k = 5$

Comprobar: Cuándo$k = 5$.

$7k - 4 = 6k + 1$

se convierte

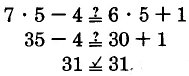
$¿7 veces 5 menos 4 es igual a 6 veces 5 más 1? Sí.$

una declaración verdadera.

La solución$7k - 4 = 6k + 1$ es$k = 5$

Conjunto de Muestras B

$-8 + x = 5$.

Solución

-8 se asocia con$x$ por adición. Deshacer el restando -8 de ambos lados. Restando -8 obtenemos$-(-8) = +8$. En realidad agregamos 8 a ambos lados.

$-8 + x + 8 = 5 + 8$

$x = 13$

Comprobar: Cuándo$x = 13$

$-8 + x = 5$

se convierte

$¿El negativo 8 más 13 es igual a 5? Sí.$

una declaración verdadera.

La solución a$-8 + x = 5$ es$x = 13$.

Set de práctica B

$y + 9 = 4$

Contestar: $y = -5$

Set de práctica B

$a - 4 = 11$

Contestar: $a = 15$

Set de práctica B

$-1 + 7 = x + 3$

Contestar: $x = 3$

Set de práctica B

$8m + 4 - 7m = (-2) (-3)$

Contestar: $m = 2$

Set de práctica B

$12k - 4 = 9k - 6 + 2k$

Contestar: $k = -2$

Set de práctica B

$-3 + a = -4$

Contestar: $a = -1$

Ejercicios

Para los siguientes 10 problemas, verificar que cada valor dado sea una solución a la ecuación dada.

Ejercicio$\PageIndex{1}$

$x - 11 = 5$,$x = 16$

Contestar

Sustituir$x = 4$ en la ecuación$4x - 11 = 5$.

$16 - 11 = 5$

$5 = 5$

$x = 4$es una solución

Ejercicio$\PageIndex{2}$

$y - 4 = -6$,$y = -2$

Ejercicio$\PageIndex{3}$

$2m - 1 = 1$,$m = 1$

Contestar

Sustituir$m = 1$ en la ecuación$2m - 1 = 1$.

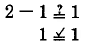
$¿2 menos 1 es igual a 1? Sí.$

$m = 1$es una solución.

Ejercicio$\PageIndex{4}$

$5y + 6 = -14$,$y = -4$

Ejercicio$\PageIndex{5}$

$3x + 2 - 7x = -5x - 6$,$x = -8$

Contestar

Sustituir$x = -8$ en la ecuación$3x + 2 - 7 = -5x - 6$.

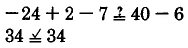
$¿El negativo 24 más 2 menos 7 equivale a 40 menos 6? Sí.$

$x = -8$es una solución.

Ejercicio$\PageIndex{6}$

$-6a + 3 + 3a = 4a + 7 - 3a$,$a = -1$

Ejercicio$\PageIndex{7}$

$-8 + x = -8$,$x = 0$

Contestar

Sustituir$x = 0$ en la ecuación$-8 + x = -8$.

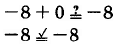
$¿El negativo 8 más 0 es igual a negativo 8? Sí.$

$x = 0$es una solución.

Ejercicio$\PageIndex{8}$

$8b + 6 = 6 - 5b$,$b = 0$

Ejercicio$\PageIndex{9}$

$4x - 5 = 6x - 20$,$x = \dfrac{15}{2}$

Contestar

Sustituir$x = \dfrac{15}{2}$ en la ecuación$4x - 5 = 6x - 20$.

$¿30 menos 5 equivale a 45 menos 20? Sí.$

$x = \dfrac{15}{2}$es una solución

Ejercicio$\PageIndex{10}$

$-3y + 7 = 2y - 15$,$y = \dfrac{22}{5}$

Resuelve cada ecuación. Asegúrese de verificar cada resultado.

Ejercicio$\PageIndex{11}$

$y - 6 = 5$

Contestar: $y = 11$

Ejercicio$\PageIndex{12}$

$m + 8 = 4$

Ejercicio$\PageIndex{13}$

$k - 1 = 4$

Contestar: $k = 5$

Ejercicio$\PageIndex{14}$

$h - 9 = 1$

Ejercicio$\PageIndex{15}$

$a + 5 = -4$

Contestar: $a = -9$

Ejercicio$\PageIndex{16}$

$b - 7 = -1$

Ejercicio$\PageIndex{17}$

$x + 4 - 9 = 6$

Contestar: $x = 11$

Ejercicio$\PageIndex{18}$

$y - 8 + 10 = 2$

Ejercicio$\PageIndex{19}$

$z + 6 = 6$

Contestar: $z = 0$

Ejercicio$\PageIndex{20}$

$w - 4 = -4$

Ejercicio$\PageIndex{21}$

$x + 7 - 9 = 6$

Contestar: $x = 8$

Ejercicio$\PageIndex{22}$

$y - 2 + 5 = 4$

Ejercicio$\PageIndex{23}$

$m + 3 - 8 = -6 + 2$

Contestar: $m = 1$

Ejercicio$\PageIndex{24}$

$z + 10 - 8 = -8 + 10$

Ejercicio$\PageIndex{25}$

$2 + 9 = k - 8$

Contestar: $k = 19$

Ejercicio$\PageIndex{26}$

$-5 + 3 = h - 4$

Ejercicio$\PageIndex{27}$

$3m - 4 = 2m + 6$

Contestar: $m = 10$

Ejercicio$\PageIndex{28}$

$5a + 6 = 4a - 8$

Ejercicio$\PageIndex{29}$

$8b + 6 + 2b = 3b - 7 + 6b - 8$

Contestar: $b = -21$

Ejercicio$\PageIndex{30}$

$12h - 1 - 3 - 5h = 2h + 5h + 3(-4)$

Ejercicio$\PageIndex{31}$

$-4a + 5 - 2a = -3a - 11 - 2a$

Contestar: $a = 16$

Ejercicio$\PageIndex{32}$

$-9n - 2 - 6 + 5n = 3n - (2) (-5) - 6n$

Ejercicios de calculadora

Ejercicio$\PageIndex{33}$

$y - 2.161 = 6.063$

Contestar: $y = 7.224$

Ejercicio$\PageIndex{34}$

$a - 44.0014 = -21.1625$

Ejercicio$\PageIndex{35}$

$-0.362 - 0.416 = 5.63m - 4.63m$

Contestar: $m = -0.778$

Ejercicio$\PageIndex{36}$

$8.078 - 9.112 = 2.106y - 1.106y$

Ejercicio$\PageIndex{37}$

$4.23k + 3.18 = 3.23k - 5.83$

Contestar: $k = -9.01$

Ejercicio$\PageIndex{38}$

$6.1185x - 4.0031 = 5.1185x - 0.0058$

Ejercicio$\PageIndex{39}$

$21.63y + 12.40 - 5.09y = 6.11y - 15.66 + 9.43y$

Contestar: $y = -28.06$

Ejercicio$\PageIndex{40}$

$0.029a - 0.013 - 0.034 -0.057 = -0.038 + 0.56 + 1.01a$

Ejercicios para la revisión

Ejercicio$\PageIndex{41}$

¿Es$\dfrac{\text{7 calculators}}{\text{12 students}}$ un ejemplo de una relación o una tasa?

Contestar: tasa

Ejercicio$\PageIndex{42}$

Convertir$\dfrac{3}{8}$% a decimal

Ejercicio$\PageIndex{43}$

¿0.4% de qué número es 0.014?

Contestar: 3.5

Ejercicio$\PageIndex{44}$

Utilice el método de agrupamiento para estimar la suma:$89 + 93 + 206 + 198 + 91$

Ejercicio$\PageIndex{45}$

Combina términos similares:$4x + 8y + 12y + 9x - 2y$.

Contestar: $13x + 18y$

Este número	es lo mismo que	este número
\(\downarrow\)	\(\downarrow\)	\(\downarrow\)
\(x\)	=	4
\(x + 7\)	=	11
\(x - 5\)	=	-1