11.2: Combinar términos similares usando suma y resta

Última actualización
Guardar como PDF

Page ID: 116399

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

ser capaz de combinar términos similares en una expresión algebraica

Combinando términos similares

A partir de nuestro examen de términos en [link], sabemos que términos similares son términos en los que las partes variables son idénticas. Como términos es un nombre apropiado ya que los términos con partes variables idénticas y diferentes coeficientes numéricos representan diferentes cantidades de la misma cantidad. Cuando estamos tratando con cantidades del mismo tipo, podemos combinarlas usando suma y resta.

Simplificación de una expresión algebraica
Una expresión algebraica puede simplificarse combinando términos similares.

Este concepto se ilustra en los siguientes ejemplos.

$\text{8 records + 5 records = 13 records.}$
Ocho y 5 del mismo tipo dan 13 de ese tipo. Hemos combinado cantidades del mismo tipo.
$\text{8 records + 5 records + 3 tapes = 13 records + 3 tapes.}$
Ocho y 5 del mismo tipo dan 13 de ese tipo. Así, tenemos 13 de un tipo y 3 de otro tipo. Hemos combinado sólo cantidades del mismo tipo.
Supongamos que dejamos que la$x$ letra represente “registro”. Entonces,$8x + 5x = 13x$. Los términos$8x$ y$5x$ son como términos. Entonces, 8 y 5 del mismo tipo dan 13 de ese tipo. Hemos combinado términos similares.
Supongamos que dejamos que la letra$x$ represente “grabar” y$y$ representar “cinta”. Entonces,
$8x + 5x + 3y = 13x + 5y$
hemos combinado sólo los términos similares.

Después de observar los problemas en estos ejemplos, podemos sugerir un método para simplificar una expresión algebraica combinando términos similares.

Combinar términos
similares Los términos similares se pueden combinar sumando o restando sus coeficientes y fijando el resultado a la variable común.

Conjunto de Muestras A

Simplifica cada expresión combinando términos similares.

$2m + 6m - 4m$. Los tres términos son iguales. Combine sus coeficientes y afije este resultado a$m$: 2 + 6 - 4 = 4.

Por lo tanto,$2m + 6m - 4m = 4m$.

Conjunto de Muestras A

$5x + 2y - 9y$. Los términos$2y$ y$-9y$ son como términos. Combinar sus coeficientes: 2 - 9 = -7.

Por lo tanto,$5x + 2y - 9y = 3x - 7y$.

Conjunto de Muestras A

$-3a + 2b - 5a + a + 6b$. Los términos similares son

$\underbrace{-3a, -5a, a}_{\begin{array} {c} {-3 - 5 + 1 = -7} \\ {-7a} \end{array}}$$\underbrace{2b,6b}_{\begin{array} {c} {2 + 6 = 8} \\ {8b} \end{array}}$

Por lo tanto,$-3a + 2b - 5a + a + 6b = -7a + 8b$.

Conjunto de Muestras A

$r - 2s + 7s + 3r - 4r - 5s$. Los términos similares son

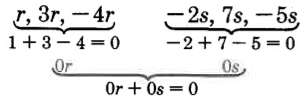
$Dos listas entre parenteos. La primera lista es r, 3r y -4r. Debajo de esta se encuentra la ecuación, 1+3-4=0. Debajo de esto está la expresión, 0r. La segunda lista es -2s, 7s y -5s. Debajo de esta se encuentra la ecuación -2+7-5=0. Debajo de esto está la expresión, 0s. Los resultados de las dos listas se pueden simplificar a 0r + 0s = 0.$

Por lo tanto,$r - 2s + 7s + 3r - 4r - 5s = 0$.

Conjunto de práctica A

Simplifica cada expresión combinando términos similares.

$4x + 3x + 6x$

Contestar: $13x$

Conjunto de práctica A

$5a + 8b + 6a - 2b$

Contestar: $11a + 6b$

Conjunto de práctica A

$10m - 6n - 2n -m +n$

Contestar: $9m - 7n$

Conjunto de práctica A

$16a + 6m + 2r - 3r - 18a + m - 7m$

Contestar: $-2a - r$

Conjunto de práctica A

$5h - 8k + 2h - 7h + 3k + 5k$

Contestar: 0

Ejercicios

Simplifica cada expresión combinando términos similares.

Ejercicio$\PageIndex{1}$

$4a + 7a$

Contestar: $11a$

Ejercicio$\PageIndex{2}$

$3m + 5m$

Ejercicio$\PageIndex{3}$

$6h - 2h$

Contestar: $4h$

Ejercicio$\PageIndex{4}$

$11k - 8k$

Ejercicio$\PageIndex{5}$

$5m + 3n - 2m$

Contestar: $3m + 3n$

Ejercicio$\PageIndex{6}$

$7x - 6x + 3y$

Ejercicio$\PageIndex{7}$

$14s + 3s - 8r + 7r$

Contestar: $17s - r$

Ejercicio$\PageIndex{8}$

$-5m - 3n + 2m + 6n$

Ejercicio$\PageIndex{9}$

$7h + 3a - 10k + 6a - 2h - 5k - 3k$

Contestar: $5h + 9a - 18k$

Ejercicio$\PageIndex{10}$

$4x - 8y - 3z + x - y - z - 3y - 2z$

Ejercicio$\PageIndex{11}$

$11 w + 3x - 6w - 5w + 8x - 11x$

Contestar: 0

Ejercicio$\PageIndex{12}$

$15r - 6s + 2r + 8s - 6r - 7s - s - 2r$

Ejercicio$\PageIndex{13}$

$|-7|m + |6|m + |-3|m$

Contestar: $16m$

Ejercicio$\PageIndex{14}$

$|-2|x + |-8|x + |10|x$

Ejercicio$\PageIndex{15}$

$(-4 + 1)k + (6 - 3)k + (12 - 4)h + (5 + 2)k$

Contestar: $8h + 7k$

Ejercicio$\PageIndex{16}$

$(-5 + 3)a - (2 + 5) b - (3 + 8)b$

Ejercicio$\PageIndex{17}$

$5 \star + 2\Delta + 3\Delta - 8 \star$

Contestar: $5\Delta - 3 \star$

Ejercicio$\PageIndex{18}$

9+10−11−12

Ejercicio$\PageIndex{19}$

$16x - 12y + 5x + 7 - 5x - 16 -3y$

Contestar: $16x - 15y - 9$

Ejercicio$\PageIndex{20}$

$-3y + 4z - 11 - 3z - 2y + 5 - 4(8 - 3)$

Ejercicios para la revisión

Ejercicio$\PageIndex{21}$

Convertir$\dfrac{24}{11}$ a un número mixto

Contestar: $2 \dfrac{2}{11}$

Ejercicio$\PageIndex{22}$

Determinar el numerador faltante:$\dfrac{3}{8} = \dfrac{?}{64}$.

Ejercicio$\PageIndex{23}$

Simplificar$\dfrac{\dfrac{5}{6} - \dfrac{1}{4}}{\dfrac{1}{12}}$

Contestar: 7

Ejercicio$\PageIndex{24}$

Convertir$\dfrac[5}{16}$ a un porcentaje.

Ejercicio$\PageIndex{25}$

En la expresión$6k$, cuántos$k$ hay

Contestar: 6