8.1: Resolver ecuaciones usando las propiedades de resta y suma de igualdad (Parte 1)
- Page ID
- 114203
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- Resolver ecuaciones usando las Propiedades de Suma y Suma de Igualdad
- Resolver ecuaciones que necesitan simplificarse
- Traducir una ecuación y resolver
- Traducir y resolver aplicaciones
Antes de comenzar, toma este cuestionario de preparación.
- Resolver: n − 12 = 16. Si te perdiste este problema, revisa el Ejemplo 2.5.6.
- Traducir en álgebra 'cinco menos que x. ' Si te perdiste este problema, revisa el Ejemplo 2.4.12.
- ¿Es x = 2 una solución a 5x − 3 = 7? Si te perdiste este problema, revisa el Ejemplo 2.5.1.
Ahora estamos listos para “llegar a las cosas buenas”. Tienes lo básico abajo y estás listo para comenzar uno de los temas más importantes en álgebra: resolver ecuaciones. Las solicitudes son ilimitadas y se extienden a todas las carreras y campos. Además, las habilidades y técnicas que aprendas aquí te ayudarán a mejorar tus habilidades de pensamiento crítico y resolución de problemas. Esto es un gran beneficio de estudiar matemáticas y te será útil en tu vida de formas que quizás no veas en este momento.
Resolver ecuaciones usando las propiedades de resta y suma de la igualdad
Comenzamos nuestro trabajo resolviendo ecuaciones en capítulos anteriores. Ha pasado un tiempo desde que vimos una ecuación, por lo que revisaremos algunos de los conceptos clave antes de ir más lejos.
Dijimos que resolver una ecuación es como descubrir la respuesta a un rompecabezas. El propósito al resolver una ecuación es encontrar el valor o valores de la variable que hacen que cada lado de la ecuación sea igual. Cualquier valor de la variable que haga verdadera la ecuación se denomina solución a la ecuación. Es la respuesta al rompecabezas.
Una solución de una ecuación es un valor de una variable que hace una declaración verdadera cuando se sustituye en la ecuación.
En las secciones anteriores, enumeramos los pasos para determinar si un valor es una solución. Los reformulamos aquí.
Paso 1. Sustituir el número por la variable en la ecuación.
Paso 2. Simplifica las expresiones en ambos lados de la ecuación.
Paso 3. Determinar si la ecuación resultante es verdadera.
- Si es cierto, el número es una solución.
- Si no es cierto, el número no es una solución.
Determinar si y =\(\dfrac{3}{4}\) es una solución para 4y + 3 = 8y.
Solución
| Sustituto\(\textcolor{red}{\dfrac{3}{4}}\) de y. | $$4\ left (\ textcolor {rojo} {\ dfrac {3} {4}}\ derecha) + 3\ stackrel {?} {=} 8\ izquierda (\ textcolor {rojo} {\ dfrac {3} {4}}\ derecha) $$ |
| Multiplicar. | $$3 + 3\ stackrel {?} {=} 6$$ |
| Agregar. | $$6 = 6\;\ marca de verificación$$ |
Dado que y =\(\dfrac{3}{4}\) da como resultado una ecuación verdadera,\(\dfrac{3}{4}\) es una solución a la ecuación 4y + 3 = 8y.
¿Y = es\(\dfrac{2}{3}\) una solución para 9y + 2 = 6y?
- Contestar
-
no
¿Y = es\(\dfrac{2}{5}\) una solución para 5y − 3 = 10y?
- Contestar
-
no
Presentamos las propiedades de resta y suma de igualdad en la resolución de ecuaciones usando las propiedades de resta y suma de igualdad. En esa sección, modelamos cómo funcionan estas propiedades y luego las aplicamos para resolver ecuaciones con números enteros. Volvimos a utilizar estas propiedades cada vez que introdujimos un nuevo sistema de números. Revisemos esas propiedades aquí.
Resta Propiedad de Igualdad
Para todos los números reales a, b y c, si a = b, entonces a − c = b − c.
Adición Propiedad de Igualdad
Para todos los números reales a, b y c, si a = b, entonces a + c = b + c.
Cuando sumas o restas la misma cantidad de ambos lados de una ecuación, todavía tienes igualdad.
Introdujimos la Propiedad de Sustracción de Igualdad anteriormente modelando ecuaciones con envolventes y contadores. La figura\(\PageIndex{1}\) modela la ecuación x + 3 = 8.
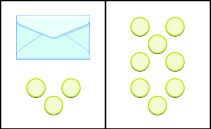
Figura\(\PageIndex{1}\)
El objetivo es aislar la variable en un lado de la ecuación. Así que 'quitamos '3 de ambos lados de la ecuación y encontramos la solución x = 5.
Algunas personas imaginan una escala de equilibrio, como en la Figura\(\PageIndex{2}\), cuando resuelven ecuaciones.
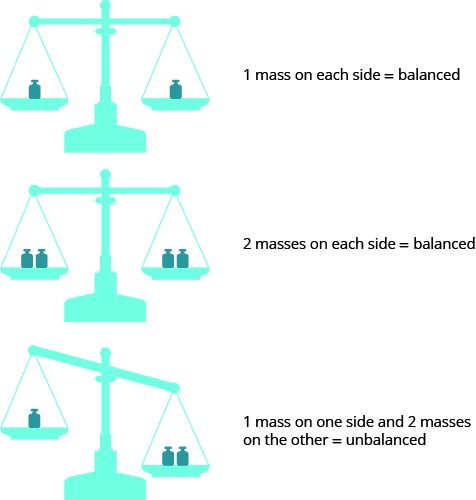
Figura\(\PageIndex{2}\)
Las cantidades a ambos lados del signo igual en una ecuación son iguales o equilibradas. Al igual que con la balanza, hagas lo que hagas a un lado de la ecuación también debes hacer al otro para mantenerlo equilibrado.
Repasemos cómo usar las Propiedades de Suma y Suma de la Igualdad para resolver ecuaciones. Necesitamos aislar la variable en un lado de la ecuación. Y comprobamos nuestras soluciones sustituyendo el valor en la ecuación para asegurarnos de que tenemos una afirmación verdadera.
Resolver: x + 11 = −3.
Solución
Para aislar x, deshacemos la suma de 11 mediante el uso de la Propiedad de Sustracción de Igualdad.
| Restar 11 de cada lado para “deshacer” la suma. | $$x + 11\ textcolor {rojo} {-11} = -3\ textcolor {rojo} {-11} $$ |
| Simplificar. | $$x = -14$$ |
Comprobar:
| Sustituye x = −14. | $$\ textcolor {rojo} {-14} + 11\ stackrel {?} {=} -3$$ |
| $$-3 = -3\;\ marca de verificación$$ |
Dado que x = −14 hace de x + 11 = −3 una declaración verdadera, sabemos que es una solución a la ecuación.
Resolver: x + 9 = −7.
- Contestar
-
x = -16
Resolver: x + 16 = −4.
- Contestar
-
x = -20
En la ecuación original del ejemplo anterior, se sumó 11 a la x, por lo que restamos 11 para 'deshacer' la suma. En el siguiente ejemplo, necesitaremos 'deshacer' la resta usando la Propiedad de Suma de Igualdad.
Resolver: m + 4 = −5.
Solución
| Agrega 4 a cada lado para “deshacer” la resta. | $$m + 4\ textcolor {rojo} {-4} = -5\ textcolor {rojo} {-4} $$ |
| Simplificar. | $$m = -9$$ |
Comprobar:
| Sustituto m = −9. | $$\ textcolor {rojo} {-9} + 4\ stackrel {?} {=} -5$$ |
| $$-5 = -5\;\ marca de verificación$$ |
La solución a m + 4 = −5 es m = −9.
Resolver: n − 6 = −7.
- Contestar
-
n = -1
Resolver: x − 5 = −9.
- Contestar
-
x = -4
Ahora revisemos resolviendo ecuaciones con fracciones.
Resolver: n −\(\dfrac{3}{8}\) =\(\dfrac{1}{2}\).
Solución
| Utilizar la Propiedad de Adición de Igualdad. | $$n -\ dfrac {3} {8}\ textcolor {rojo} {+\ dfrac {3} {8}} =\ dfrac {1} {2}\ textcolor {rojo} {+\ dfrac {3} {8}} $$ |
| Encuentra la pantalla LCD para sumar las fracciones a la derecha. | $$n -\ dfrac {3} {8} +\ dfrac {3} {8} =\ dfrac {4} {8} +\ dfrac {3} {8} $$ |
| Simplificar. | $$n =\ dfrac {7} {8} $$ |
Comprobar:
| Sustituto n =\(\textcolor{red}{\dfrac{7}{8}}\). | $$\ textcolor {rojo} {\ dfrac {7} {8}} -\ dfrac {3} {8}\ stackrel {?} {=}\ dfrac {1} {2} $$ |
| Restar. | $$\ dfrac {4} {8}\ stackrel {?} {=}\ dfrac {1} {2} $$ |
| Simplificar. | $$\ dfrac {1} {2} =\ dfrac {1} {2}\;\ marca de verificación$$ |
La solución comprueba.
Resolver: p −\(\dfrac{1}{3}\) =\(\dfrac{5}{6}\).
- Contestar
-
\(p = \frac{7}{6}\)
Resolver: q −\(\dfrac{1}{2}\) =\(\dfrac{1}{6}\).
- Contestar
-
\( q = \frac{2}{3}\)
En Resolver ecuaciones con decimales, resolvimos ecuaciones que contenían decimales. Revisaremos esto a continuación.
Resolver a − 3.7 = 4.3.
Solución
| Utilizar la Propiedad de Adición de Igualdad. | $$a - 3.7\ textcolor {rojo} {+3.7} = 4.3\ textcolor {rojo} {+3.7} $$ |
| Agregar. | $$a = 8$$ |
Comprobar:
| Sustituir a = 8. | $$\ textcolor {rojo} {8} - 3.7\ stackrel {?} {=} 4.3$$ |
| Simplificar. | $4.3 = 4.3\;\ marca de verificación$$ |
La solución comprueba.
Resolver: b − 2.8 = 3.6.
- Contestar
-
b = 6.4
Resolver: c − 6.9 = 7.1.
- Contestar
-
c = 14
Resolver ecuaciones que necesitan simplificarse
En los ejemplos hasta este punto, hemos podido aislar la variable con una sola operación. Muchas de las ecuaciones que encontremos en álgebra tomarán más pasos para resolver. Por lo general, necesitaremos simplificar uno o ambos lados de una ecuación antes de usar las Propiedades de Suma o Suma de Igualdad. Siempre debes simplificar lo más posible antes de intentar aislar la variable.
Resolver: 3x − 7 − 2x − 4 = 1.
Solución
El lado izquierdo de la ecuación tiene una expresión que debemos simplificar antes de intentar aislar la variable.
| Reorganizar los términos, utilizando la Propiedad Conmutativa de Adición. | $$3x - 2x - 7 - 4 = 1$$ |
| Combina términos similares. | $$x - 11 = 1$$ |
| Agrega 11 a ambos lados para aislar x. | $$x - 11\ textcolor {rojo} {+11} = 1\ textcolor {rojo} {+11} $$ |
| Simplificar. | $$x = 12$$ |
| Cheque. Sustituye x = 12 en la ecuación original. | $$\ begin {split} 3x - 2x - 7 - 4 &= 1\\ 3 (\ textcolor {rojo} {12}) - 7 - 2 (\ textcolor {rojo} {12}) - 4 &= 1\\ 36 - 7 - 24 - 4 &= 1\\ 29 - 24 - 4 &= 1\\ 5 - 4 &= 1\\ 1 &= 1\;\ marca de verificación\ final split} $$ |
La solución comprueba.
Resolver: 8y − 4 − 7y − 7 = 4.
- Contestar
-
y = 15
Resolver: 6z + 5 − 5z − 4 = 3.
- Contestar
-
z = 2
Resolver: 3 (n − 4) − 2n = −3.
Solución
El lado izquierdo de la ecuación tiene una expresión que debemos simplificar.
| Distribuir a la izquierda. | $$3n - 12 - 2n = -3$$ |
| Utilice la Propiedad Conmutativa para reorganizar los términos. | $$3n - 2n - 12 = -3$$ |
| Combina términos similares. | $$n - 12 = -3$$ |
| Aísle n usando la Propiedad de Adición de Igualdad. | $$n - 12\ textcolor {rojo} {+12} = -3\ textcolor {rojo} {+12} $$ |
| Simplificar. | $$n = 9$$ |
| Cheque. Sustituye n = 9 en la ecuación original. | $$\ begin {split} 3 (n-4) - 2n &= -3\\ 3 (\ textcolor {rojo} {9} - 4) - 2\ cdot\ textcolor {rojo} {9} &= -3\\ 3 (5) - 18 &= -3\\ 15 - 18 &= -3\\ -3 &= -3\;\ marca de verificación\ end {split} $$ |
La solución comprueba.
Resolver: 5 (p − 3) − 4p = −10.
- Contestar
-
p = 5
Resolver: 4 (q + 2) − 3q = −8.
- Contestar
-
q = -16
Resolver: 2 (3k − 1) − 5k = −2 − 7.
Solución
Ambos lados de la ecuación tienen expresiones que debemos simplificar antes de aislar la variable.
| Distribuir a la izquierda, restar a la derecha. | $$6k - 2 - 5k = -9$$ |
| Utilice la Propiedad Conmutativa de Adición. | $$6k - 5k - 2 = -9$$ |
| Combina términos similares. | $$k - 2 = -9$$ |
| Deshacer la resta usando la Propiedad de Suma de Igualdad. | $$k - 2\ textcolor {rojo} {+2} = -9\ textcolor {rojo} {+2} $$ |
| Simplificar. | $$k = -7$$ |
| Cheque. Dejar k = −7. | \ [\ begin {split} 2 (3k - 1) - 5k &= -2 - 7\\ 2 [3 (\ textcolor {rojo} {-7}) -1] - 5 (\ textcolor {rojo} {-7}) &= -2 - 7\\ 2 (-21 - 1) - 5 (-7) &= -9\\ 2 (-22) + 35 &= -9\ -9 = -9\;\ marca de verificación\ final {división} $$ |
La solución comprueba.
Resolver: 4 (2h − 3) − 7h = −6 − 7.
- Contestar
-
h = -1
Resolver: 2 (5x + 2) − 9x = −2 + 7.
- Contestar
-
x = 1


